港口物流与环境质量关系的实证研究

黎振强， 周秋阳， 彭平锋

(湖南理工学院 经济与管理学院， 湖南 岳阳414006)

当前， 中国港口总体规模位于世界前列， 据统计， 2018 年末中国港口拥有生产用码头泊位23919 个， 其中万吨级及以上泊位2444 个， 港口货物吞吐量持续增长. 在2018 年和2019 年的世界十大港口排名中， 中国的港口上榜率居全球第一. 随着港口规模的扩大和港口物流的发展， 港口环境保护问题日益突出. 2019 年中国绿色港口发展大会提出了要加快绿色港口建设步伐， 推进港口经济绿色发展的行动方案. 因此， 本文基于环境库兹涅茨假说， 以港口废水排放为例， 实证分析港口物流与环境质量之间的内在关系， 对于把握两者所处的阶段， 提出相应的环境治理建议， 实现港口与环境协调发展具有现实意义.

1 文献回顾

国内学者以库兹涅茨假说为理论基础在经济增长、贸易发展与城市化进程等方面分析环境质量问题， 取得了丰富的研究成果. 最早受到学者关注的是经济增长与环境污染之间的关系， 杨素昌、马素琳[1]的研究表明城市经济增长与环境的EKC 呈倒N 型曲线； 詹新宇、曾傅雯[2]认为经济规模的扩大会加剧环境污染. 在中国加入世贸组织后， 国内学者对贸易与环境污染之间的关系展开了研究， 常乃磊、李帅[3]以工业“三废”作为环境污染指标， 利用工业“三废”数据计算环境污染综合指数， 发现无论长期还是短期， 出口均加剧了中国环境污染程度， 而进口在长期内会减轻环境污染， 短期内则会增加环境污染. 胡飞[4]以中国东部和中部地区为例， 认为出口规模扩大会加剧东部和中部地区的环境污染， 但进口规模的变化不会对环境污染产生明显的影响. 随着城市化发展， 中国城市化进程对生态环境的影响也成为学者关注的热点， 郭佳、何雄伟等[5]分析了人口城镇化对地区环境污染的影响， 研究发现EKC 曲线无法拟合人口城镇化与环境污染之间的函数关系. 王华星、石大千[6]则从政策评价的角度， 利用双重差分方法评估了低碳城市建设对城市雾霾污染的影响， 发现低碳城市建设能够显著降低城市的雾霾污染.

根据文献梳理可知， 国内学者主要从经济、贸易、城市化等方面利用环境库兹涅茨假说验证与环境质量之间的关系， 但对于港口与环境质量的内在关系研究相对不足. 鉴于此， 本文基于已有的研究成果， 以环境库兹涅茨理论为基础构建模型， 探讨港口物流与工业废水排放之间的关系， 并为港口与环境之间的协调发展提出可供参考的建议.

2 实证研究及分析

2.1 数据说明及变量选择

选取上海、天津、大连、广州、深圳、厦门、福州、连云港、南京、南通、苏州、宁波、温州、青岛、烟台和日照16 个沿海城市及各自所拥有的港口为研究对象， 搜集整理各城市在2000～2015 年的工业废水排放总量及港口吞吐量的数据(有关工业三废的排放数据公布周期为五年， 所以观测的时间点截至2015 年). 为了减小异方差， 先对数据进行对数化处理， 检验其平稳性， 然后建立静态模型和动态模型， 探讨废水排放与港口吞吐量之间的内在联系. 借鉴已有研究成果， 本文选取了以下变量建立模型：

(1) 因变量为工业废水排放量， 记为water. 一方面， 港口经济活动会直接产生废水， 另一方面， 港口处于水陆的交界区域， 是人类各种生产活动的重要承载区， 其优越的地理位置及强大的运输功能将促进各种重工业的产生及发展， 从而间接增加工业废水的排放， 因此选择工业废水排放量作为衡量水污染的指标. 图1 中的左图反映了各城市在2000～2015 年工业废水排放量的时间趋势， 从绝对值来看， 大部分城市的工业废水排放量基本呈平稳上升趋势， 且上升幅度不明显， 原因可能是各城市都比较重视环境问题， 实施的环境保护措施减缓和遏制了工业废水的排放.

(2) 解释变量为各城市的港口物流发展水平， 以港口吞吐量表示， 记为tt， 其平方项和立方项分别记为tt2和tt3. 图1 中的右图反映了各沿海港口在2000～2015 年吞吐量的变化趋势， 可以看出， 各港口的吞吐量呈现绝对的增长趋势， 而且增长速度明显， 说明港口物流发展态势良好.

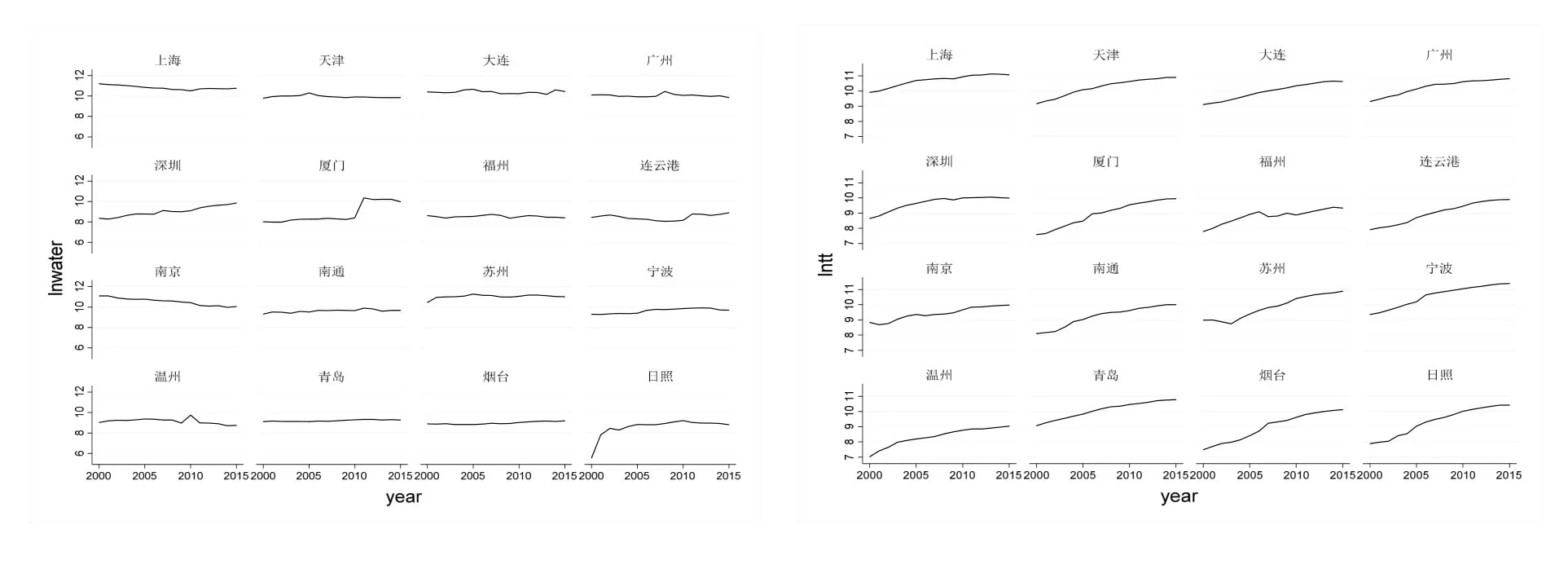
图1 2000～2015 年工业废水排放量及港口吞吐量时间趋势

(3) 控制变量

影响环境质量的因素众多， 为了减少或避免遗漏变量、共线性及自由度损失等问题， 本文选择了已有文献中出现频率较高的变量为控制变量：

① 对外贸易水平(trade). 贸易水平对环境污染的影响主要体现在国与国之间的“污染转嫁”、进出口产品在运输过程中所造成的污染等， 贸易所造成的环境污染主要包括水污染及大气污染.

② 国内生产总值(gdp). 衡量城市经济发展水平的指标很多， 考虑到国内生产总值对大部分经济变量都会产生影响， 为了减弱内生性， 选择该变量来衡量城市经济发展.

③ 城镇化率(rcity). 人口城镇化与环境污染之间存在一定的关系， 城市人口的增加会造成废水排放量的增加， 从而对环境产生一定影响， 因此将该变量作为控制变量， 以城镇人口与总人口的比值衡量.

除上述因素之外， 产业结构、固定资产投资等也会对环境污染产生一定程度的影响， 鉴于面板协整检验要求的变量个数有限， 而且相关变量数据存在缺失， 因此将其余变量纳入随机扰动项. 有关变量的数据来源于wind 数据库、各城市国民经济和社会发展统计公报和统计年鉴.

2.2 变量的统计特征及平稳性检验

对数据进行对数化处理之后， 变量之间的相关性及统计特征见表1. 从数据本身来看， 港口物流水平的发展会加剧水环境的污染， 二者呈正相关， 其它变量也是如此， 经济发展、对外贸易和城镇化水平的提高均会加重水污染. 从统计特征来看， 每个变量的整体标准差介于0.9～1.5 之间， 组内标准差和组间标准差大部分小于1， 说明数据选取有意义.

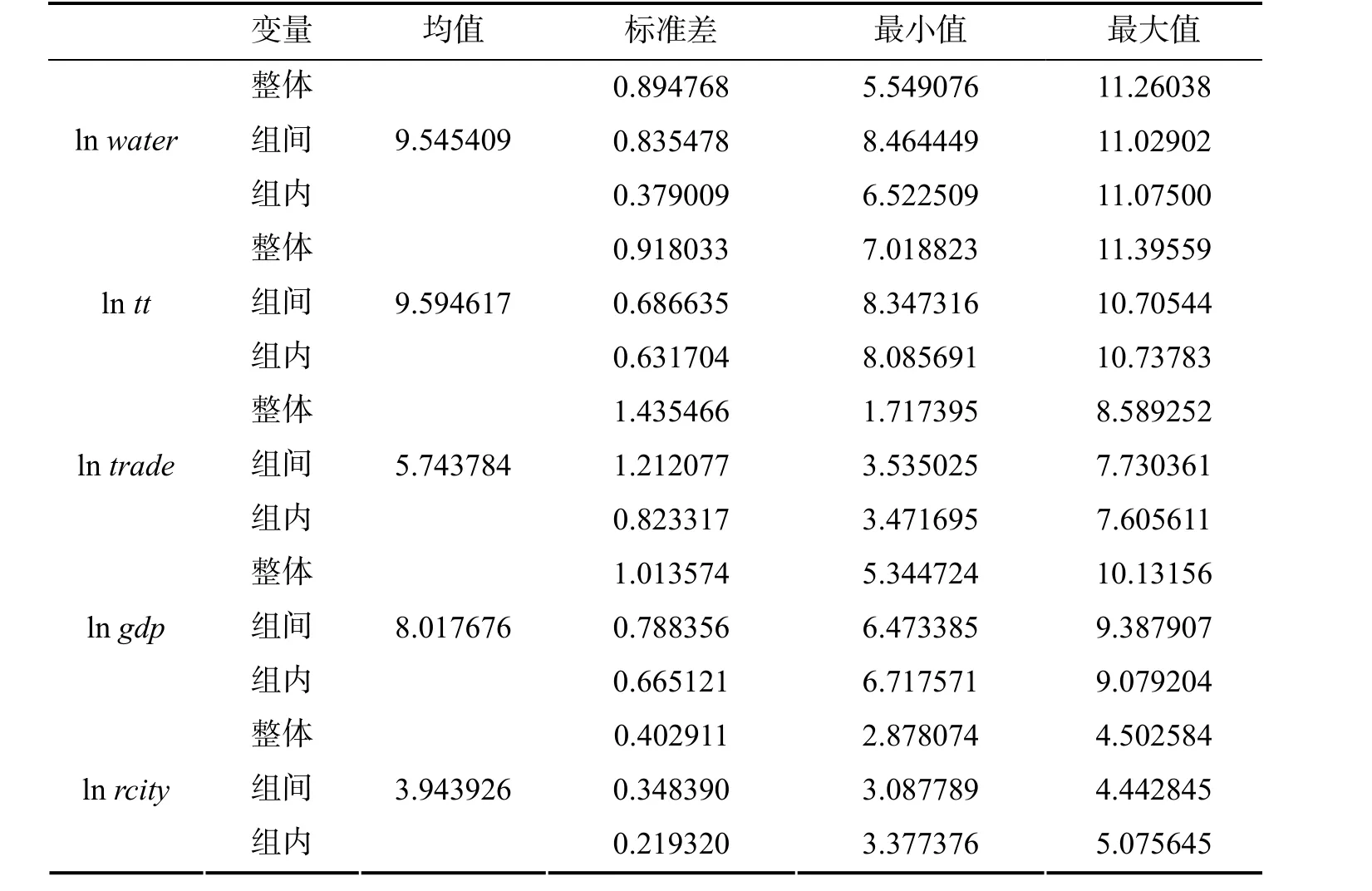
表 1 变量的描述性统计

在本文面板数据中， 大多数城市的工业废水排放量具有一定的时间趋势， 但整体上升趋势不明显； 港口吞吐量的变化则呈明显的上升趋势. 因此， 采用IPS 检验方法对原数据进行面板单位根检验， 检验结果见表2. 所有变量一阶差分的P 值均为0.0000， t-bar 统计量均小于1%水平的临界值， 所以拒绝原假设， 即所有变量均是一阶单整变量.

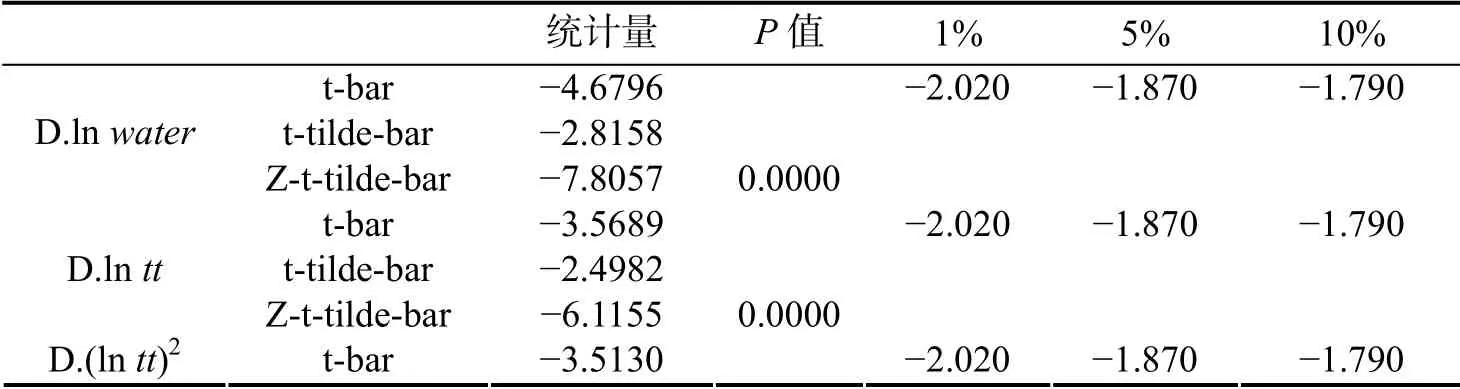
表 2 变量的单位根 IPS 检验结果

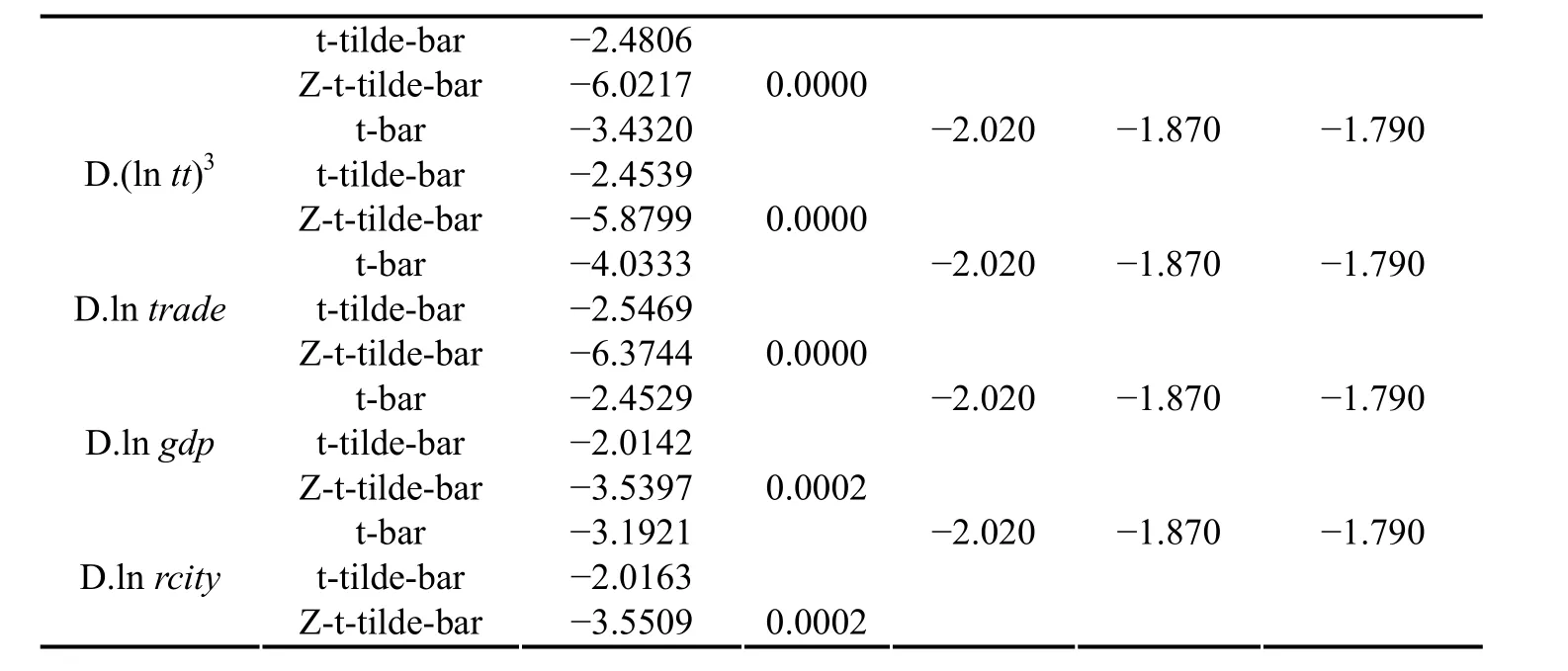
D.(ln tt)3 D.ln trade D.ln gdp D.ln rcity t-tilde-bar -2.4806 Z-t-tilde-bar -6.0217 0.0000 t-bar -3.4320 -2.020 -1.870 -1.790 t-tilde-bar -2.4539 Z-t-tilde-bar -5.8799 0.0000 t-bar -4.0333 -2.020 -1.870 -1.790 t-tilde-bar -2.5469 Z-t-tilde-bar -6.3744 0.0000 t-bar -2.4529 -2.020 -1.870 -1.790 t-tilde-bar -2.0142 Z-t-tilde-bar -3.5397 0.0002 t-bar -3.1921 -2.020 -1.870 -1.790 t-tilde-bar -2.0163 Z-t-tilde-bar -3.5509 0.0002

2.3 模型构建

2.3.1 协整检验

根据上文， 所有变量均为一阶单整变量， 因此可进行协整检验， 以便确定变量之间是否存在长期关系. 考虑到数据的时间维度比较大， 故采用Pedroni 检验法， 检验结果见表3. 三种统计量的P 值均为0.0000， 因此拒绝原假设， 即所有变量之间都存在协整关系.

2.3.2 静态模型设定

为了确定是建立固定效应模型还是随机效应模型， 首先采用豪斯曼检验法进行检验， 检验结果表明两种回归估计的标准误差即聚类稳健标准误差与普通标准误差相差约0.5 倍， 相差不是太大. 为使检验更加准确， 再进行过度识别(xtoverid)检验， 判断究竟是使用固定效应模型还是随机效应模型， 检验结果见表4. 其中P值为0.0000， 故拒绝原假设， 应建立固定效应模型.

本文借鉴常用的EKC 模型构建方法， 研究港口物流的发展对水资源污染的影响及二者的EKC 曲线形状. 不考虑时间和个体差异[7]， 设定静态面板模型为

表3 协整检验结果

表4 静态模型设定检验检验结果

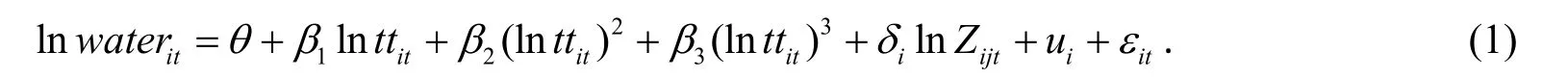
其中ln water表示水污染情况， ln tt表示港口物流发展水平， Z 表示控制变量， Z ={ln trade， ln gdp， ln rcity}， θ 表示截距项， β 和δ 分别表示变量的边际效应， ui表示个体异质性， εit表示随机误差项， 下标i 表示第i 个省份( i= 1，2， …， 16)， 下标t 表示第t 期( t= 1，2， …， 16)， 下标j 表示影响水污染的第j 个控制变量. βi(i =1，2，3)的取值决定了EKC 曲线的形状， 根据回归系数的符号及显著性可将EKC 曲线分为6 种情况， 见表5.

2.3.3 静态模型估计结果

首先采用LSDV 法进行固定效应模型的估计. 除此之外， 由于本文所使用的面板数据的时间跨度为16 年， 因此对扰动项可能存在的组内自相关、组间异方差及组间同期相关进行了检验， 结果表明数据确实存在组间异方差、组内自相关和组间同期相关. 为了便于比较， 还进行了PCSE 和全面FGLS 估计， 三种方法的估计结果见表6. 不难看出， ln tt、(ln tt)2及(ln tt)3的系数非常显著， 所以三次项模型的设立合理， 检验结果表明EKC 曲线形状呈倒N 型. 从影响系数及对应的P 值可以看出， 港口物流的发展对水污染具有显著影响； 从拟合效果来看， 模型的可决系数较高， 说明曲线拟合较好.

表5 EKC 曲线形状分类

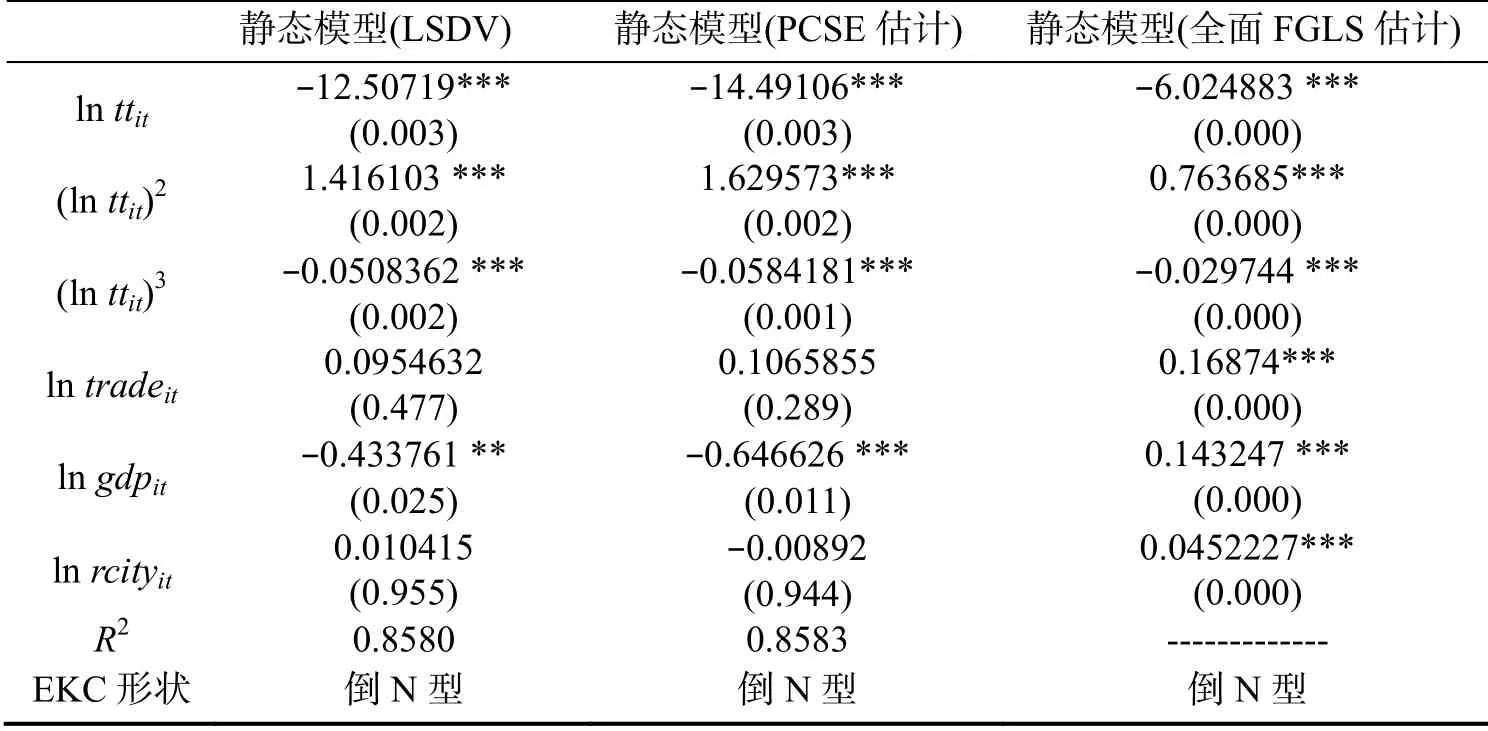
表6 静态模型估计结果

2.3.4 动态模型的设定及估计结果

根据废水排放的时序来看， 水污染具有滞后性， 即当年的污染程度会对之后的年份造成影响， 因此将水污染的滞后项作为解释变量引入模型中， 运用GMM 方法进行估计. 经过多次检验发现， 被解释变量滞后一阶最为合适， 且动态模型的形式与静态模型的形式相同， 为三次项形式. 对于动态面板模型， 由于将因变量的滞后项作为解释变量引入到方程中， 造成解释变量与随机扰动项相关， 从而产生内生性. 作为一致估计， 差分GMM 成立的前提是扰动项不存在自相关， 因此可以通过检验扰动项的差分是否存在一阶与二阶自相关来判断扰动项是否存在自相关， 结果见表7. 根据检验结果， 当阶数为一阶时， P 值为0.0999，可在10%的显著性水平下拒绝原假设， 认为扰动项的差分存在一阶自相关； 当阶数为二阶时， P 值为0.7994， 所以可接受原假设， 认为扰动项的差分不存在二阶自相关. 综上， 接受“扰动项无自相关”的原假设， 所以采用差分GMM 进行动态模型估计是合适的， 其基准模型设定为

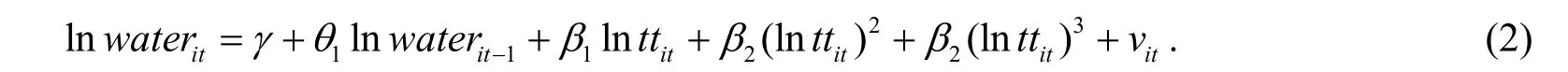
逐个引入控制变量对扩展模型

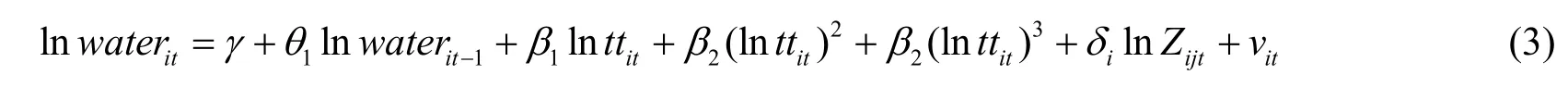
进行估计， 估计结果见表8.

表7 扰动项自相关检验结果

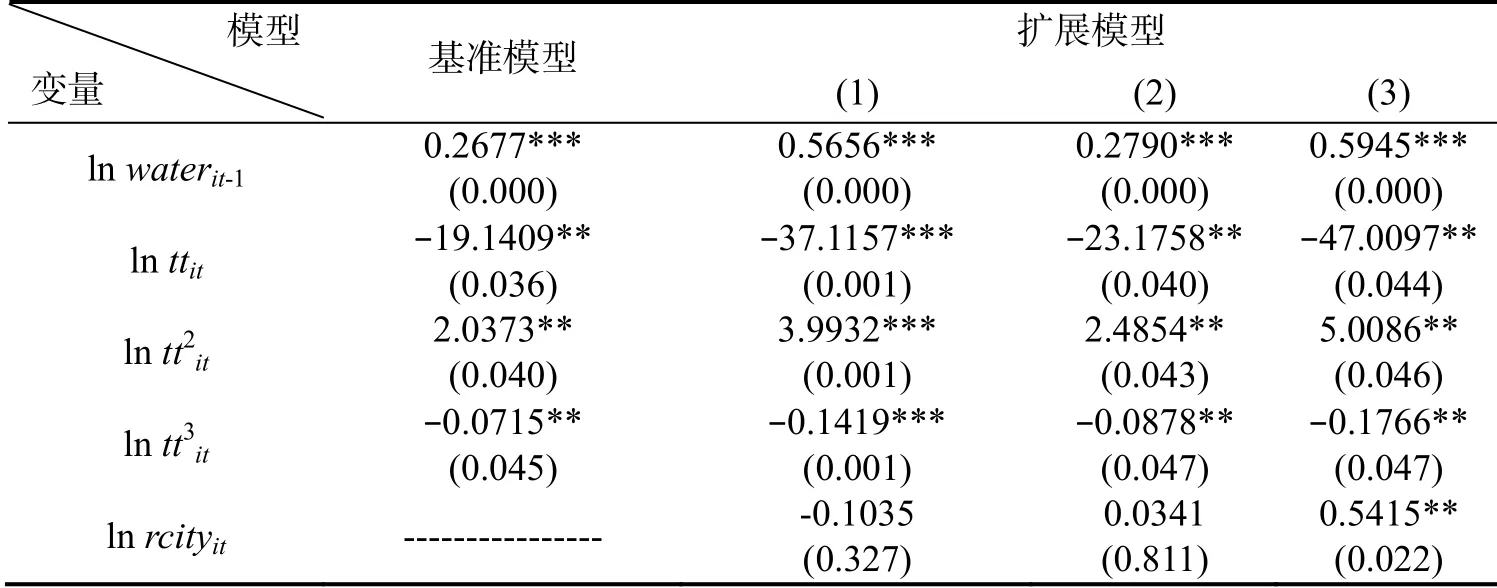
表8 动态模型估计结果

注： (1) *， **， ***分别表示在10%， 5%和1%下是显著的； (2) 括号内的数字为系数估计的P 值.

根据动态模型估计结果， 不管是基准模型还是扩展模型， 主要变量的估计系数都显著， 且模型都通过了Sargan 检验， 说明本文所采用的工具变量均有效， 因此三次项模型的建立是合理的. 从估计系数来看， ln waterit-1的系数无论是在基准模型还是扩展模型中均显著为正， 说明我国水污染存在明显的惯性， 且其系数值稳定在0.26～0.60 之间， 这意味着若保持其它条件不变， 前期遗留的水污染对当前环境的影响最高将达到60%， 也就是说， 如果忽视当期所产生的污染问题， 那么在之后的时期无论采取多少措施来治理污染问题， 其所产生的积极作用都将被之前所滞留的污染所覆盖， 因此必须要及时治理当期的污染. 解释变量lnittt 不论是在静态模型还是在动态模型中， 其系数均显著为负， 说明港口物流水平的提高可以抑制水污染问题， 但不可否认的是， 港口物流水平的提高也会产生水污染， 最终的影响效果要取决于两种作用各自的大小. 对于其它控制变量而言， 当期经济发展水平(lnitgdp )的提高将加重水污染， 而前期经济发展水平( ln gdpit-1)的提高将有效缓解水污染， 说明经济发展对水污染的影响存在滞后效应.

2.3.5 模型结果对比

静态面板模型和动态面板模型的估计结果均表明， 港口物流与环境污染之间存在EKC 效应， 二者呈倒N型的曲线关系， 废水排放量随港口物流的发展呈先下降后上升再下降的趋势. 图2 为静态模型和动态模型对应的EKC 曲线， 两种模型所对应的EKC 曲线形状大体相仿， 主要区别在于曲线的极大值不同， 动态模型EKC 曲线的极大值明显小于静态模型EKC 曲线的极大值. 当港口吞吐量小于T1(或者D1)时， 废水排放量随港口吞吐量的上升而下降， 主要原因包括： ①各港口城市经济的快速发展， 资源和环境面临压力， 为了节约资源、保护环境， 各港口城市加强了环境保护治理力度， 采取一系列环保措施有效遏制了破坏环境的行为， 废水、废气、废弃物的排放减少， 港口环境得到了一定的保护； ②各城市大力发展港口经济， 加强了交通运输条件建设， 提升了污染处理技术， 改进了港口作业方式， 使得港口发展对环境的积极作用大于消极影响. 根据废水排放和吞吐量的时间趋势， 大部分城市T1(D1)出现的时间点集中在2005、2006 和2007 年前后， 可能的主要原因有： 2004① 年1 月1 日起《中华人民共和国港口法》开始实施， 同时各大港口也相应出台了港口条例和港口管理办法， 法律法规的颁布实施在一定程度上促进了港口与环境之间的协调发展； 2008② 年中国举办奥运会， 加大了环保方面的监督管理力度， 因此在这几个年份， 废水排放量达到极小值. 当港口吞吐量处于T1～T2(或D1～D2)时， 废水排放量将随港口的发展而增加， 主要原因一是存在时滞性， 如当期的污染对后期的影响， 二是2008 年受金融危机冲击， 经济的稳定和恢复成为了重中之重， 暂时忽视环境问题， 废水排放量随港口的发展而增加. 当前， 我国大部分港口城市处于EKC 曲线的上升阶段， 少数城市已经接近极大值点， 因此， 要加强港口的环境建设， 实现港口与环境之间的协调发展.

图2 EKC 曲线

3 结论与启示

本文以上海、天津、大连、广州等16 个沿海城市2000～2015 年的工业废水排放总量及港口吞吐量的数据为基础， 分别构建静态模型和动态模型， 实证分析了港口物流与工业废水排放量之间的关系， 得到如下几点结论：

(1) 港口物流与工业废水排放量之间存在EKC 效应， 二者呈倒N 型曲线关系， 废水排放量随港口物流的发展呈先下降后上升再下降的趋势.

(2) 大部分港口城市处于EKC 曲线的上升阶段， 少数城市已经接近极大值点， 但整体上16 个港口城市的港口物流与环境质量之间还未到达协调发展阶段.

(3) 港口工业废水污染处理存在时滞， 如果对当前已经出现的水污染问题不进行有效治理， 前期滞留的水污染问题将大大影响下期以及未来的水环境治理成效， 造成资源的浪费， 影响后期的治理效率.

目前我国港口废水等污染物的排放对生态环境的影响仍然比较严重， 所以各港口城市政府要贯彻绿色发展理念， 完善绿色港口的评价体系， 正确处理港口经济与环境保护之间的关系； 各港口要建立健全港口污染物监测体系， 实时监测记录港口企业各个作业环节各种污染物的排放量， 跟踪分析排污数据变化趋势， 及时处理违法违规排放事故. 此外， 企业要积极研发， 引进新技术、新材料和新设备， 有效控制废水等污染物的排放.