1 000 kV干字型铁塔风振系数研究
黄明祥,卞宏志,张建勋,赵云龙,翁兰溪
(1.福建省电力有限公司建设分公司,福建福州 350012;2.福州大学电气工程与自动化学院,福建福州 350108;3.福建省电力勘测设计院有限公司,福建福州 350008)
0 引言
研究干字型铁塔外形、质量突变等因素对铁塔风振响应的影响,保证风振系数的准确取值成为铁塔工程亟待解决的首要问题之一[1].现有的风工程研究方法有理论分析、现场监测、风洞试验和数值模拟4大类.Li等[2]通过理论分析方式,建立一种典型输电线路系统在强风荷载作用下的概率评估方法.吴新桥等[3]通过自主开发的新型加速度传感器,对强风作用下能盘线输电铁塔进行实时在线监测,所得数据接近实际值.赵爽等[4]、李正良等[5]通过风洞试验揭示了塔线耦合的机理,较为完整地分析整体系统的风振响应,所得结果与事故记录较为一致.数值模拟方法简便易得,且能够较为准确地反映出结构体系动力响应特点[6-8].聂建波等[9]、王飞等[10]采用有限元建模的方法,通过数值模拟得到不同高度层风荷载并施加到铁塔模型上,分析得到塔身和横担处位移时程、轴力时程和风振系数.
风振系数研究是铁塔的抗风设计关键问题之一,以往的研究中忽略了横担及横隔面质量、挡风面积的突变对铁塔风振响应和风振系数计算的影响.本文针对干字型铁塔外形、质量突变等问题,利用AutoCAD铁塔组装图准确计算铁塔挡风面积,在有限元环境中建立铁塔杆梁混合模型,通过瞬态动力分析得到位移时程数据,进而计算铁塔风振系数,并与建筑规范的风振系数取值进行对比,分析形状与质量突变条件下的特高压铁塔的风振系数分布特性,同时与传统经验公式求解挡风面积所得到的风振系数进行比较.
1 有限元杆梁模型及模态分析
针对福州-厦门1 000 kV特高压工程干字塔JC 321022进行研究,该塔型式美观且结构易于构造,而且指标经济、维护方便.图1为铁塔尺寸及有限元模型,塔高h为86.8 m,呼高60 m,10 m高度基准风速v10为39 m·s-1.根据AutoCAD铁塔组装图建立铁塔有限元模型,横隔梁及塔身主材采用梁单元,其余杆件采用杆单元,整个模型共有6 209个节点和7 780个单元,其中包含7 298个梁单元和482个杆单元.
在ANSYS中对铁塔进行模态分析,所得铁塔前三阶振型如图2所示.铁塔前两阶模态分别为x向和y向平动模态,第三阶模态为扭转振动模态,模态频率依次为1.649 8、1.680 1、2.411 3 Hz.本文铁塔动力特性分析主要研究沿线路方向的振动,因此重点考虑铁塔y向平动振型.

图1 铁塔尺寸及有限元模型(单位:mm)Fig.1 Tower size and finite element model(unit:mm)

图2 铁塔前三阶模态Fig.2 First three modes of the tower
2 风荷载计算
JC 321022干字型铁塔具有多个横担和横隔面,致使塔段质量和挡风面积发生突变.在计算风荷载时,为准确分析铁塔各部分动力特性,将铁塔沿高度简化为分段加载模型,如图3所示.采用线性滤波法中的自回归模型数值方法模拟脉动风速,风速模拟主要分为7个步骤[11-12].
1)采用Davenport谱为校验谱.

式中:K为地面粗糙度系数;x0=1 200 f/v10,f为频率;v10为离地10 m高度处的基准风速.
2)计算脉动风协方差矩阵R.
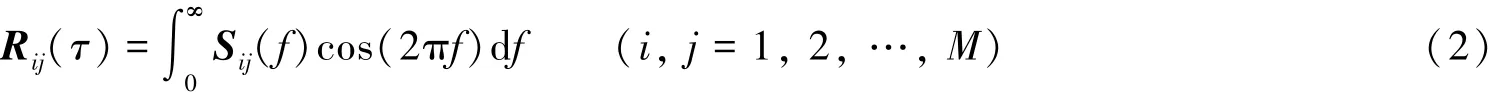
式中:Sij为空间两点脉动风互功率谱.
3)计算自回归系数矩阵ψk.

式中:ψk为M×M阶矩阵,Rp为p×M×M阶矩阵,p为模型阶数.
4)求解给定方差的随机过程N(t).

式中:Δt为时间步长,由上述步骤得出的R,结合式(4)可以求出N(t).
5)求解多维脉动风速时程.
6)采用指数律计算h高度处的平均风速vh.

式中:α为风剖面指数;h为铁塔高度;其风速剖面示意图如图4(a)所示.
7)平均风速与脉动风速叠加获得总风速.
其风速模拟时的参数取值如表1所示.图4(b)和(c)分别为采用Davenport谱模拟得到的铁塔在57.5 m高度处的风速时程曲线和风功率谱对比图,该处风速时程曲线在200 s内的峰值达到了72.36 m·s-1,且脉动风速模拟谱与校验谱吻合,表明模拟的风速时程较为准确.
由《1 000 kV架空输电线路设计规范》[13]可知,作用于铁塔第i塔段的风荷载时程可按下式计算.

图3 铁塔分段模型Fig.3 Tower segmentation model

式中:vi(t)为模拟得到的铁塔第i塔段中心风速时程;μsi、Ai分别为第i塔段风荷载体型系数和挡风面积,通过模拟出的风速时程数据即可得到风荷载时程数据.

图4 风速剖面、铁塔57.5 m处风速时程和校验谱Fig.4 Wind speed profile、time history and calibration spectrum at 57.5 m

表1 风速模拟主要参数Tab.1 Main parameters of wind speed simulation
3 铁塔风振系数
由于横担及横隔面导致塔段质量、挡风面积和体型系数的变化,对铁塔风振系数产生较大影响,现行规范给出的计算方法无法准确得到干字型铁塔风振系数.所以,为保证特高压工程抗风设计的可靠性,应采用时域法对铁塔风振系数进行相应计算.目前主流的时域法风振系数计算方法有两种,分别是位移法[14]和加速度法[15],本文计算风振系数拟采用位移法,其计算过程考虑了铁塔的一阶振动圆频率,能较好地反映出铁塔的风振特性.铁塔h高度处风振系数βi(i为铁塔分段,i=1,2,…,n)按下式计算.

式中:Psi、Pfi分别为静风效应、动风效应;Mi为铁塔分段质量;ω1为结构一阶振动圆频率;ω0为基本风压,ω0=v210/1600,v10为基准风速;σli、μzi分别为铁塔h高度处塔段位移均方差、风压高度变化系数;g为峰值因子;其它参数同前.
3.1 铁塔挡风面积计算
针对沿线路风向、基准风速为39 m·s-1工况下的铁塔进行动力特性分析和风振系数计算.为得到铁塔各塔段的风荷载时程,需统计各塔段的挡风面积,将铁塔分段投影到迎风面计算净面积,根据铁塔组装图所给角钢及节点板等连接钢材的尺寸,通过AutoCAD计算各塔段挡风面积Ai,并统计出塔身轮廓所围的面积,以便计算每一段的风荷载体形系数.为简化计算,工程研究人员总结了铁塔挡风面积Ai求解经验公式:

式中:l1i、l2i分别为第i塔段上宽和下宽;di为塔段段高;φ为铁塔构架的填充系数,对塔高超过80 m的干字型铁塔,填充系数可取0.165~0.22;通过式(8)计算挡风面积的方法记为经验法.图5给出AutoCAD法计算值和经验法在不同填充系数下的计算值分布,铁塔高度h为塔段中心离地高度,为比较不同填充系数下经验法计算值与AutoCAD法计算值的差异,经验公式填充系数分别取0.165、0.192 5、0.22.由图5可知,两种方法所得挡风面积分布特征较为一致,但在下导线横担以下,不同计算值之间差异较大.
3.2 干字型铁塔风振系数分布特性
得到各塔段风荷载时程后,加载到干字型铁塔有限元模型相应节点上进行瞬态动力分析.图6是铁塔在沿线路风向和39 m·s-1风速下高度分别为17.1、57.5、80.4 m的位移时程,高度越高,铁塔位移响应越剧烈,且各塔段位移在同一时间点随高度增加而增大,铁塔在80.4 m高度处位移峰值达到了0.119 m.
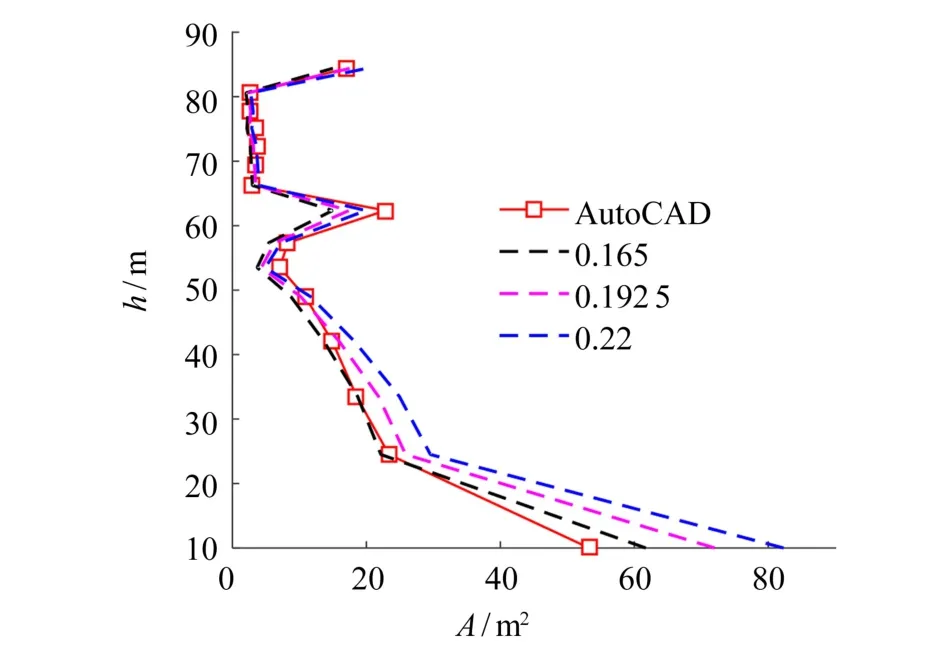
图5 挡风面积计算值比较Fig.5 Comparison of calculated values of windshield area

图6 铁塔位移响应Fig.6 Tower displacement response
图7 给出干字型铁塔各塔段沿高度变化的位移响应特性.由图7可得:1)铁塔的位移响应沿高度增加而呈弯曲性增大,表明铁塔的高度越高,位移值越大,结构振动越明显;2)在三个填充系数值当中,填充系数为0.192 5时所得到的铁塔位移响应结果与由AutoCAD法所得到的结果最为接近,从位移响应的角度可以表明经验法能够较好地满足风振响应分析.
根据铁塔位移响应结果,通过式(7)计算铁塔风振系数.图8给出铁塔各塔段风振系数计算值以及高耸结构设计规范取值和建筑结构荷载规范取值分布[16-17],其中塔段6和塔段11为横隔面增设处,塔段8和塔段15为横担,塔段7为塔身变坡处.由图8可知:1)对于干字型铁塔,风振系数随高度增加而非线性、曲折性增大;2)在横担及横隔面处风振系数变化幅度较大,这是由于该处塔段质量和挡风面积发生突变;3)铁塔各塔段风振系数的高耸结构设计规范取值和建筑结构荷载规范取值与时域法计算值相差较大,表明两类规范不适用于干字型耐张塔这类铁塔风振系数的计算分析.
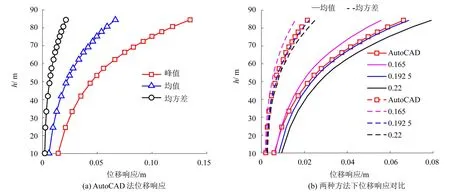
图7 铁塔位移响应特性Fig.7 Displacement response characteristics of iron towers
图9 给出由两种挡风面积计算方法所得的的铁塔各塔段风振系数对比图,可以看出:由两种计算方法所得的塔段风振系数总体趋势吻合,经验法基本满足风振系数分析和计算,但在横担及横隔面处,经验法所得风振系数与AutoCAD法结果差异较大,这是因为经验法无法准确计算节点板挡风面积.沿高度分别计算不同方法所得到的挡风面积加权平均值AH和风振系数加权平均值βH,计算公式如下:
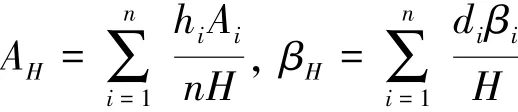

图8 风振系数分布Fig.8 Wind vibration coefficient distribution

图9 风振系数对比Fig.9 Wind vibration coefficient comparison
经验法所得挡风面积加权平均值随着填充系数的增大而增大,风振系数加权平均值随着填充系数的增大而减小,填充系数为0.192 5时所得挡风面积和风振系数加权均值与AutoCAD法所得结果较为一致.结果详见表2所示.
为分析风振系数计算值的分布特性影响因素,由式(7)整理得:

表2 加权平均值对比Tab.2 Weighted average comparison

式中:PZi单位为m·kg-1;MAi为铁塔第i塔段质量与挡风面积的比值,单位为kg·m-1;PZi与MAi的乘积即为动风荷载与静风荷载之比,其中,PZi随塔段离地高度增加而弯曲性增大,整体趋势趋同于铁塔各塔段位移均方差.MAi和风振系数的分布如图10所示.可以看出:1)风振系数分布特征趋同于MAi分布,表明用时域法计算铁塔风振系数时,主要影响因素为质量和挡风面积的比值;2)MA6、MA11较大,这是该处横隔面的增设,导致塔段质量激增,而对挡风面积值影响较小.对该塔进行优化设计时,在保证整塔力学特性良好的情况下,可以针对质量与挡风面积比值进行结构调整,以保证铁塔的风振系数加权平均值符合规范要求的同时,减少工程造价.

图10 质量与面积比值分布Fig.10 Ratio distribution of mass and area
4 结语
1)AutoCAD法与填充系数为0.192 5时的经验法计算挡风面积和风振系数较为接近,但由于经验法无法准确计算横隔面增设处节点板的挡风面积,导致在横隔面处面积计算值差异较大,继而导致两种方法所得到的风振系数在横隔面处差异较大;采用AutoCAD法可以准确计算铁塔风振系数,但其挡风面积统计过程较为繁琐,因此在进行铁塔抗风设计时,简易计算风振系数可以采用填充系数为0.192 5时的经验法,准确计算风振系数可以采用AutoCAD法.
2)铁塔各塔段风振系数随高度增加而非线性、曲折性增大,在横担及横隔面处塔段质量、挡风面积和风振系数均发生突变;风振系数分布趋同于质量与挡风面积的比值分布,即风振系数计算值的主要影响因素为质量和挡风面积.

