高烈度区高低墩曲线刚构桥地震分析

彭文毅, 唐波

高烈度区高低墩曲线刚构桥地震分析

彭文毅, 唐波

(中南林业科技大学 土木工程学院, 湖南 长沙, 410004)

为了了解高烈度区高低墩曲线刚构桥的地震响应特性, 选取云南某高低墩曲线刚构桥为工程背景, 利用MIDAS软件中的纤维单元对其进行非线性动力弹塑性分析, 得到桥梁的动力特性与地震动响应。结果表明:地震动在顺桥向加载下, 墩底控制截面出现最强地震动响应, 且高墩比低墩更为剧烈; 在横桥向加载下, 低墩截面出现最强的地震动响应, 抗弯能力的变化趋势更加敏感。高、低墩桥墩横向抗推刚度相差明显, 加载时主梁横向扭转。

高烈度; 高低墩曲线刚构桥; 有限元; 设计地震; 罕遇地震; 非线性

随着桥梁建设迅速发展, 曲线刚构桥因其良好的空间跨越性被普遍地建设。特别是在城市匝道桥和山区公路桥中, 广泛地采用高低墩曲线刚构桥的桥梁形式, 以满足场地的空间布置要求。但高低墩曲线刚构桥这类不规则桥型, 本身结构受力十分复杂, 对其进行地震分析更是十分必要的[1]。

迄今为止, 众多学者根据不同工程背景, 采用不同方法对高低墩刚构桥进行了大量分析研究。连梦磊[2]等对高低墩连续拱桥进行ABAQUS有限元研究, 对比分析了考虑桥墩高差的多点激励的地震响应; 程志友[3]等对大跨高低墩连续梁桥的动力特性进行分析, 对比了在对称情况下和高低墩情况下的地震动响应差异; 游惠敏[4]等采用有限元软件Midas Civil建立全桥三维模型研究了纵向横系梁对双薄壁高低墩连续刚构桥抗震性能影响分析。沈自宇[5]等以某连续刚构桥为背景, 通过时程分析法研究了墩间距对动力特性及地震反应的影响。何伟[6]等探讨了在近断层地震动加载下, 高低墩连续刚构桥的桥墩损伤情况和地震动响应。

从以上研究来看, 针对高低墩曲线刚构桥这类复杂结构桥型的抗震分析较少。本文以云南省境内某公路高低墩曲线桥研究对象, 先后通过子空间迭代法、反应谱分析法以及地震动时程分析法。研究了桥梁的自振特性和地震动内力与位移响应, 以期了解高烈度区高低墩曲线刚构桥的地震反应特性, 为结构有效抗震设计提供参考。

1 工程概况

云南省境内某公路3跨高低墩曲线刚构桥, 采用3 × 25 m连续箱梁, 设计平曲线半径70 m, 桥梁全长85.08 m。梁高1.8 m, 顶板宽度为8.7 m, 其厚度为0.25 m。底板宽4.6 m, 在跨中位置厚0.25 m, 在支点位置厚0.45 m。腹板在跨中位置的厚度为0.60 m, 在支点位置的厚度为0.80 m。挑臂长度为2.05 m, 挑臂根部厚度为0.40 m。1号高墩和2号低墩均采用板式墩, 壁厚1.2 m, 墩高分别为8.0、4.5 m, 基础采用2 m厚承台, 两墩与梁体固结, 连接全桥上下部结构整体, 桥梁总体布置图及箱梁截面图见图1、图2。

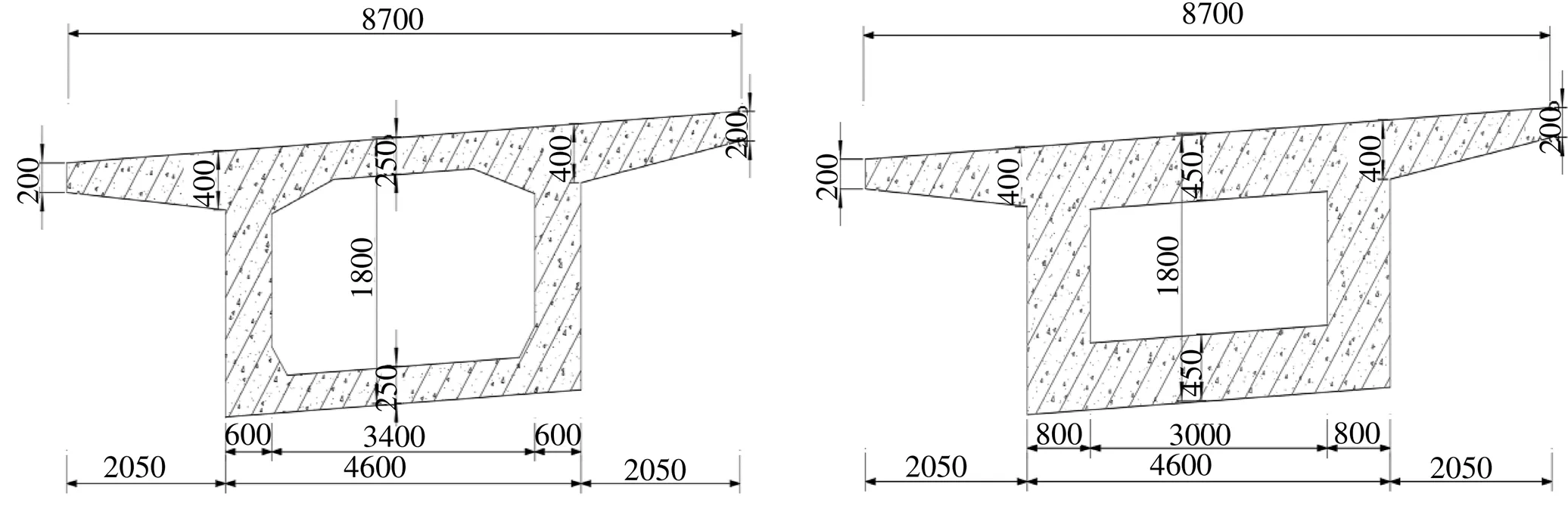
图2 箱梁截面图(单位: mm)

图3 混凝土本构模型

2 有限元计算模型

全桥建模时, 上部曲线箱梁结构利用以直代曲方法, 使用短距离、多频次划分单元的方式拟合曲线梁。桥墩与梁固结, 采用弹塑性纤维单元对其进行非线性动力弹塑性分析, 混凝土本构模型使用Kent Park模型[7](如图3所示)。建模时墩底与地面固结, 不考虑桩基作用, 并且作为中小跨径桥梁不考虑多点激励问题。分析对象的三维空间计算模型见图4。

图4 有限元计算模型

3 桥梁动力特性

为了得到桥梁的动力特性, 需要对结构进行特征值分析。特征值分析也称为自由振动分析, 结构的质量和刚度决定其振型形状、自振频率和固有周期等。本文通过子空间迭代法计算结构的动力特性, 得到的前10阶自振频率及振型以进行自振模态分析[8], 计算结果见表1, 前十阶振型图见图5。由表1和图5可知: 由于高低墩的刚度在顺桥桥向和横桥向有较大差异, 所以在顺桥向加载时, 高墩将发生较强的剪力、扭矩和弯矩, 以至于出现高墩纵弯曲; 在横向地震作用下, 低墩产生较强的剪力、扭矩和弯矩, 以至于出现低墩纵弯曲。

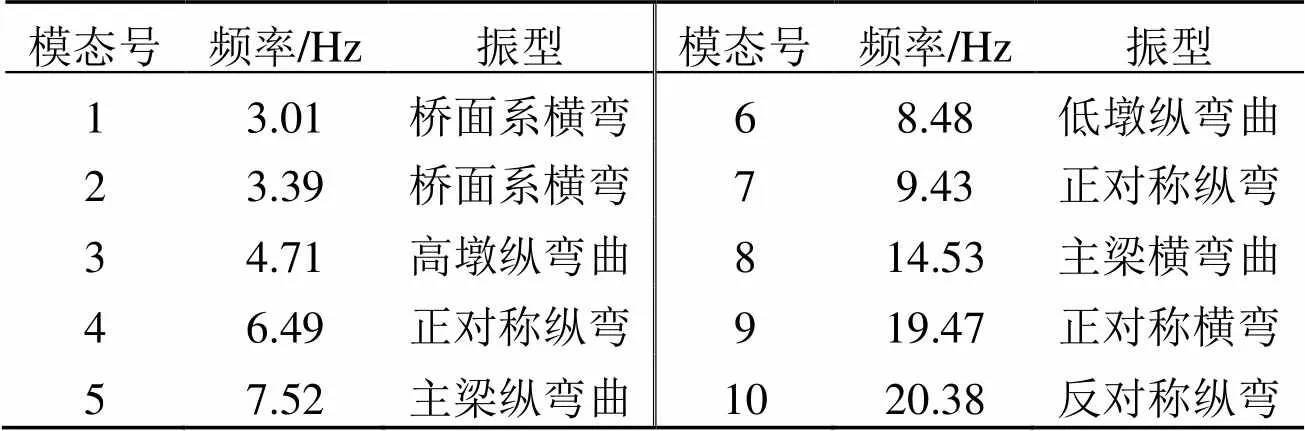
表1 桥梁前10阶频率及振型

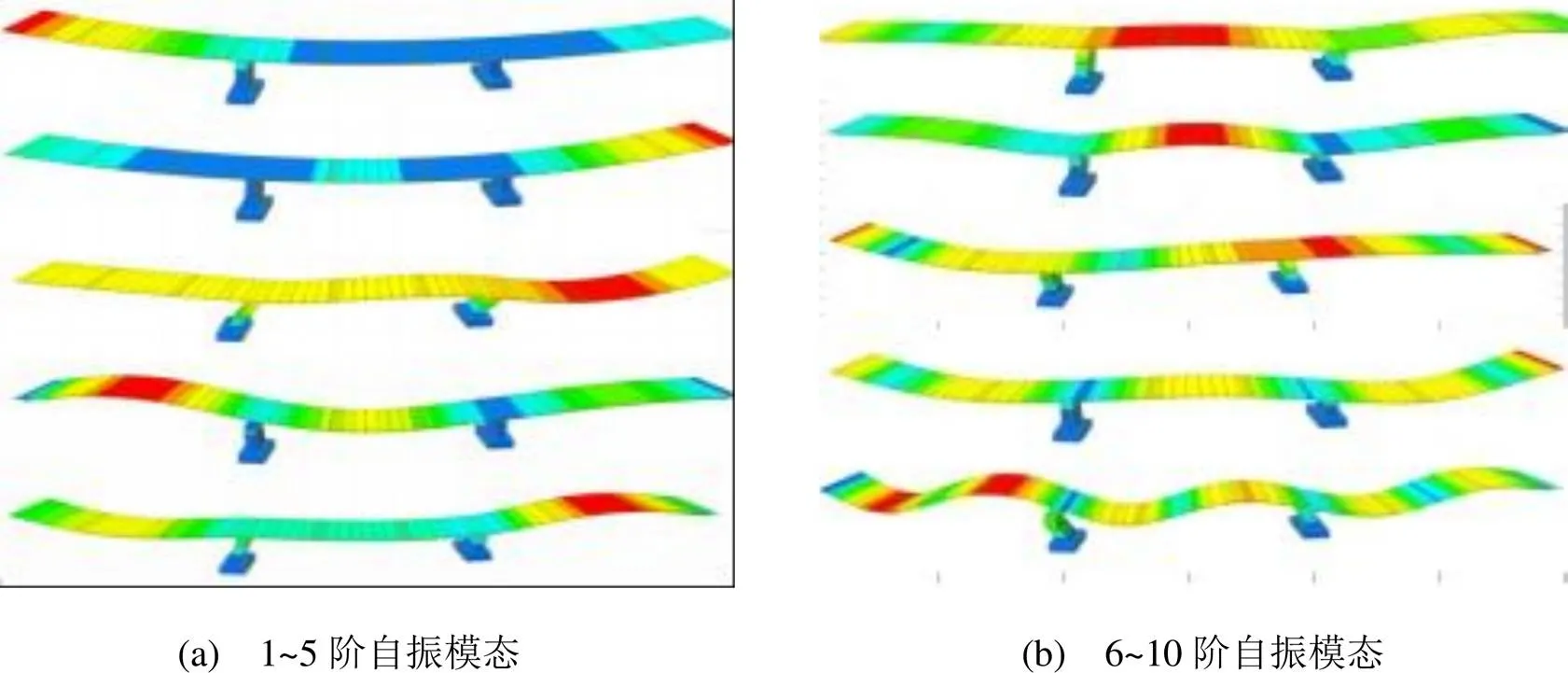
图5 前10阶振型图

4 反应谱分析

4.1 反应谱分析理论

反应谱分析是通过计算每个自由度系统的最大反应, 并将它们在一定程度上组合成最大反应的水平, 来形成多自由度系统最大地震反应的方法。以单自由度系统的最大反应为纵坐标, 自振周期为横坐标, 对不同周期的单自由度系统用同一地震波输入, 按照不同阻尼比计算, 可以得到一系列地震反应谱曲线[9]。

反应谱理论将结构动力学特性与地震特征的关系综合考虑, 又保持了静力理论形式。该桥场地特征周期为0.4 s, 抗震设防类别为D类, 地震基本烈度为8度。结合上述原理与桥梁抗震设计要求, 得到设计地震反应谱曲线如图6所示。

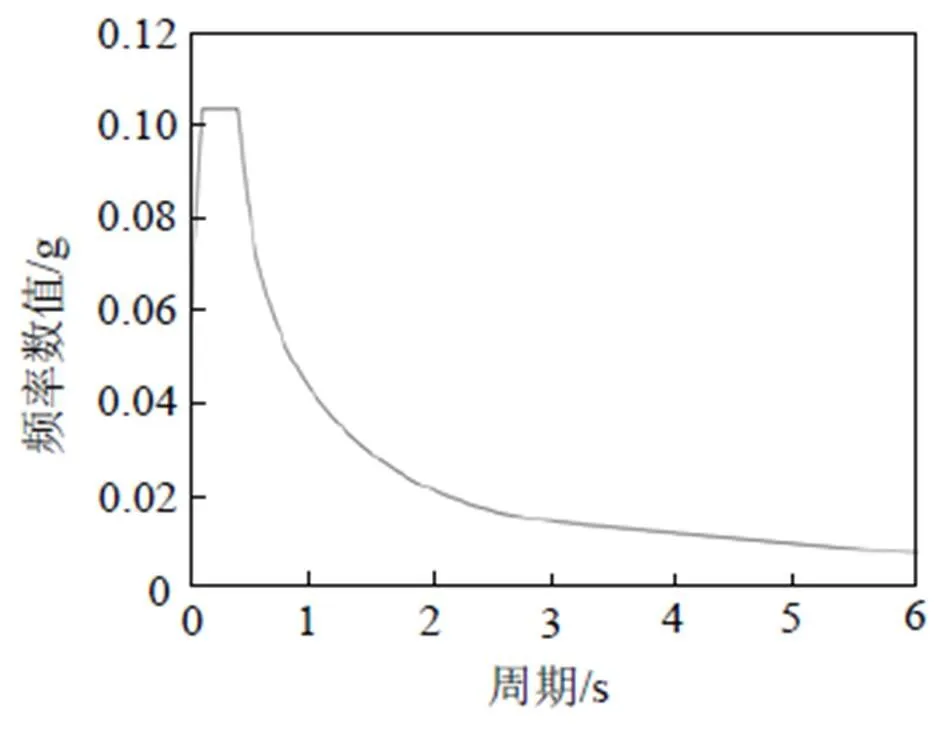
图6 反应谱曲线

4.2 反应谱地震响应

由图7可知, 最大应力位置出现在桥梁中跨和桥梁两墩墩底位置处; 最小应力位置出现在桥梁边跨。刚构体系桥, 桥梁中跨与两墩固结相连, 限制其水平位移。边跨一侧与桥墩固结, 另一侧位于支座之上, 只对竖向的位移进行约束, 因此桥梁中跨应力大于边跨应力。以桥墩为分析对象, 可以发现墩顶与墩底都会产生较大应力。建模时不考虑桩基作用, 墩底与地面固结, 导致墩底受约束应力比墩顶更大。当刚构体系桥受到地震动作用时, 桥墩是吸收地震能量抵抗结构倾覆的最不利位置, 所以对桥墩控制截面内力进行研究分析。

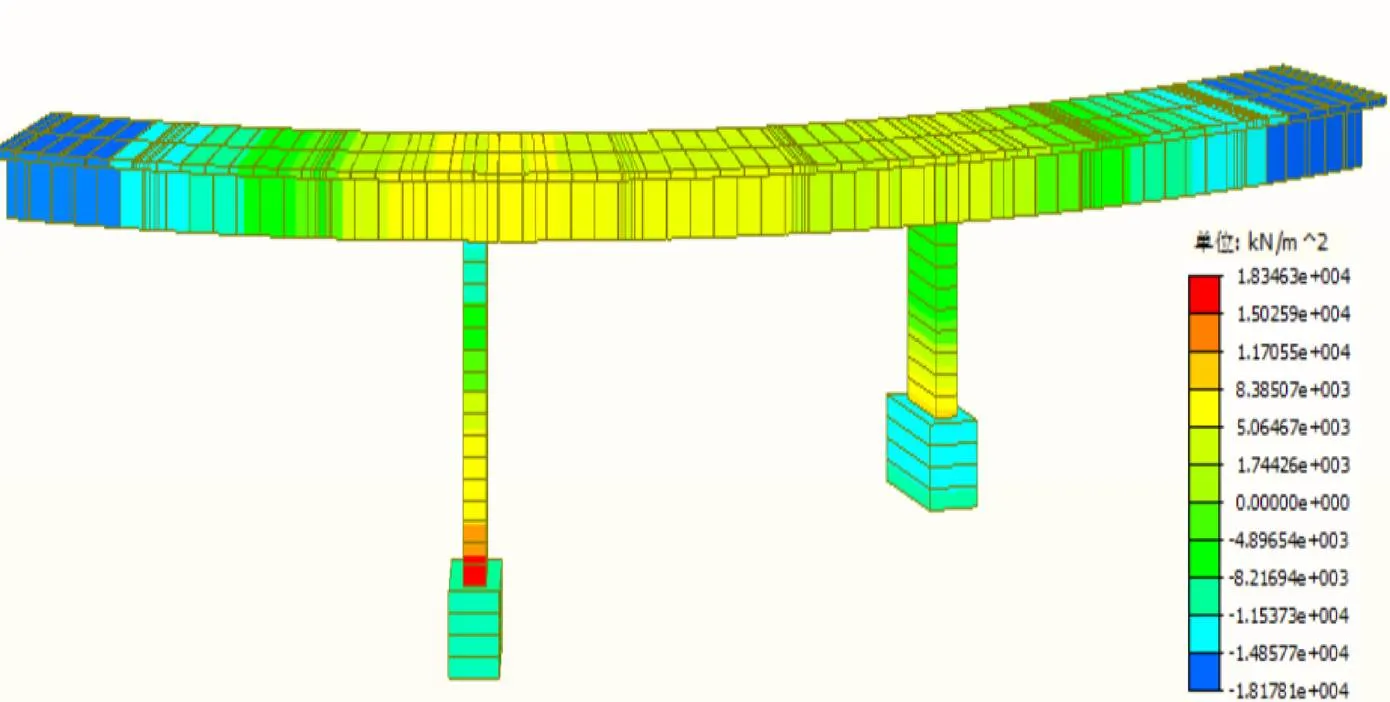
图7 全桥等效应力图

桥墩控制截面的内力最大值如表2、表3所示。墩底最大弯矩均发生在顺桥向地震加载情况下的截面顺桥向, 此时高墩底最大弯矩27 618 kN·m, 低墩顶最大弯矩为19 612 kN·m。对于高墩而言, 三向地震作用下, 截面顺桥向弯矩都显著超过横桥向弯矩。究其原因, 可能是在地震动激励下, 高墩出现了更为强烈的纵向弯曲, 这导致顺桥向承受内力更大。对于低墩而言, 墩底最大地震响应弯矩值均发生在横桥向地震动加载, 于低墩截面横桥向方向出现。此时低墩最大弯矩为7 907 kN·m, 而高墩最大弯矩为4 494 kN·m。说明低墩的抗弯能力在横桥向的地震响应中需要更高的需求。因此, 对高低墩曲线刚构桥的抗震分析必须考虑横桥向地震效应。

表2 各向地震动作用下墩底控制截面内力最大值 /(kN·m)

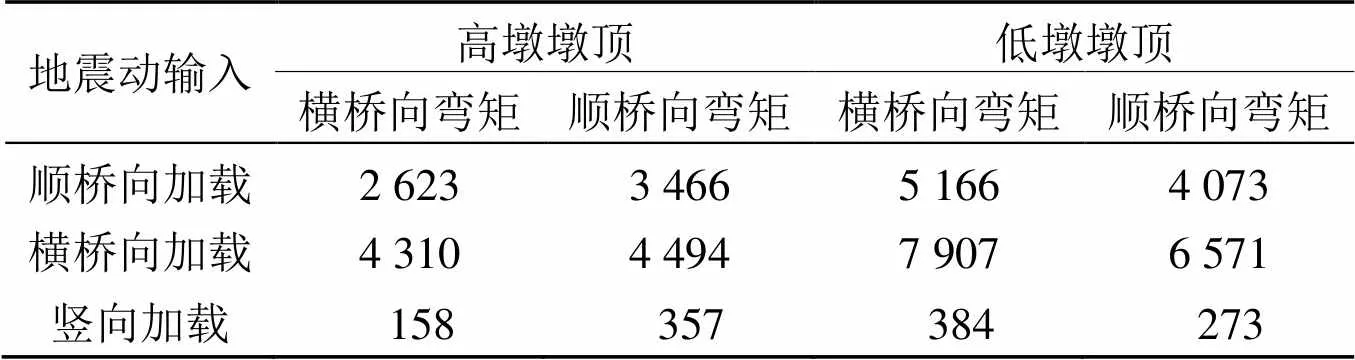
表3 各向地震动作用下墩顶控制截面内力最大值 /(kN·m)

5 地震动时程分析

5.1 动力分析原理

研究地震动作用下, 多自由度结构的动力学基本平衡方程[10]为: []{} + []{} +[]{} = [] []{′′}。式中:为质量矩阵;为阻尼矩阵;为刚度矩阵;为单位向量;为位移矢量;′′为地震波加速度。在时程分析中, 地震波的选择是影响结构反应特性的一个重要因素, 不同的地震波、不同方向的输入会导致结构地震反应存在明显差异, 对地震波加载持续时间的选取也非常重要。

本文根据《公路桥梁抗震设计细则》(JTG/T B02-01-2008)中规定, 采用3组罕遇地震时程曲线加载, 取3组计算结果中的最大值。地震加速度时程曲线如图8所示, 持续时间包含了时程加速度的最值, 通常为结构基本周期的5~10倍[11], 综合考虑持时定为10 s。

由上述反应谱结果可知曲线桥沿割线方向(顺桥向)地震响应最大, 在该桥中即采用沿前后端部支座中点连线方向。同时单薄壁墩抗弯能力的变化趋势对横桥向的地震响应十分敏感, 并且利用纤维有限元模型建模时, 竖向时程加载同样不能忽视。综合考虑, 对全桥分别采用“顺桥向加竖向”加载和“横桥向加竖向”加载。

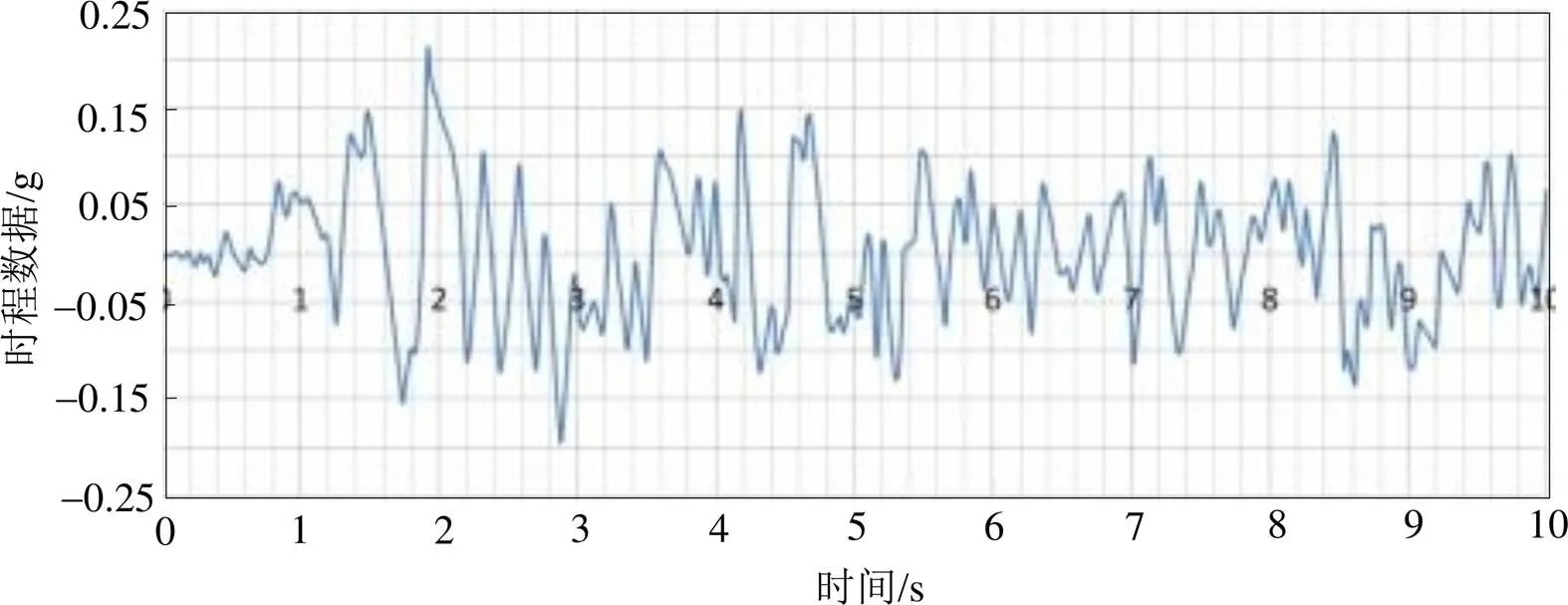
图8 地震加速度时程曲线

5.2 内力响应分析

表4为罕遇地震作用下桥墩底截面抗震验算数据。结果表明在罕遇地震作用下, 高、低桥墩关键截面弯矩均小于截面的等效屈服弯矩。满足罕遇地震作用下桥墩截面弯矩应小于截面等效抗弯屈服弯矩 M eq (考虑轴力)的性能要求。此时混凝土一般不会出现压溃现象, 可以确定该结构未完全丧失承载力, 即满足“桥梁大震不倒”设计要求。

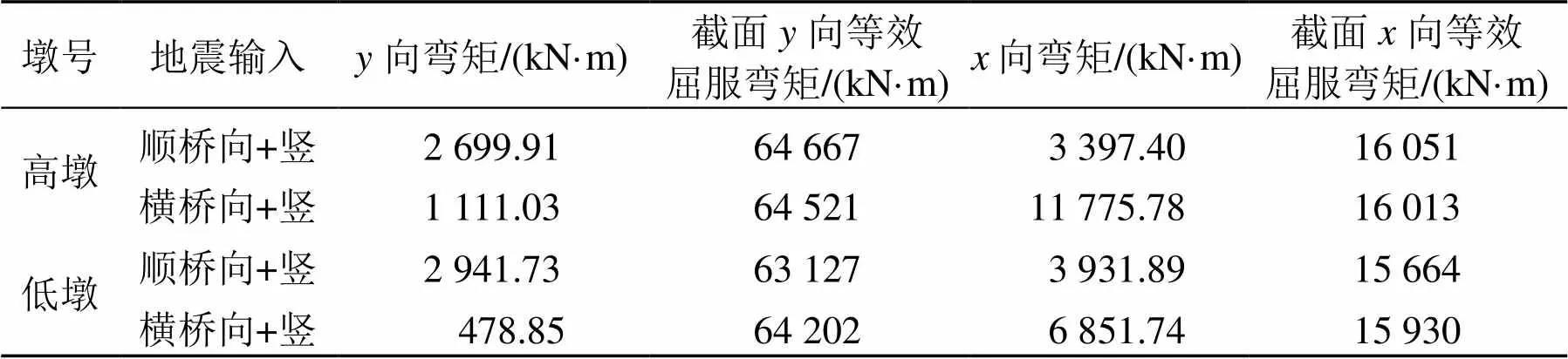
表4 罕遇地震作用下桥墩底截面抗震验算结果

5.3 位移响应分析

图9为墩顶位置沿纵桥向的位移时程图。由图可知该桥在纵向地震作用下, 墩顶的位移变化趋势基本一致。但是高墩的位移响应相较低墩更强, 其最大位移响应达到了14.12 mm。低墩的最大位移响应为10.63 mm, 比高墩小了24.7%。图10为墩顶沿横桥向的位移时程图, 由图可知横桥向方向虽然高墩位移响应仍强于低墩, 但是两墩位移方向正好相反。因为两桥墩的高度不同, 导致墩身横向刚度差异较大, 且上部结构横向约束较小, 使两墩位移方向和大小相去甚远。这会造成主梁产生扭转, 所以在抗震设计时, 必须结合横向稳定, 从而进一步提高该类桥梁的抗震性能。

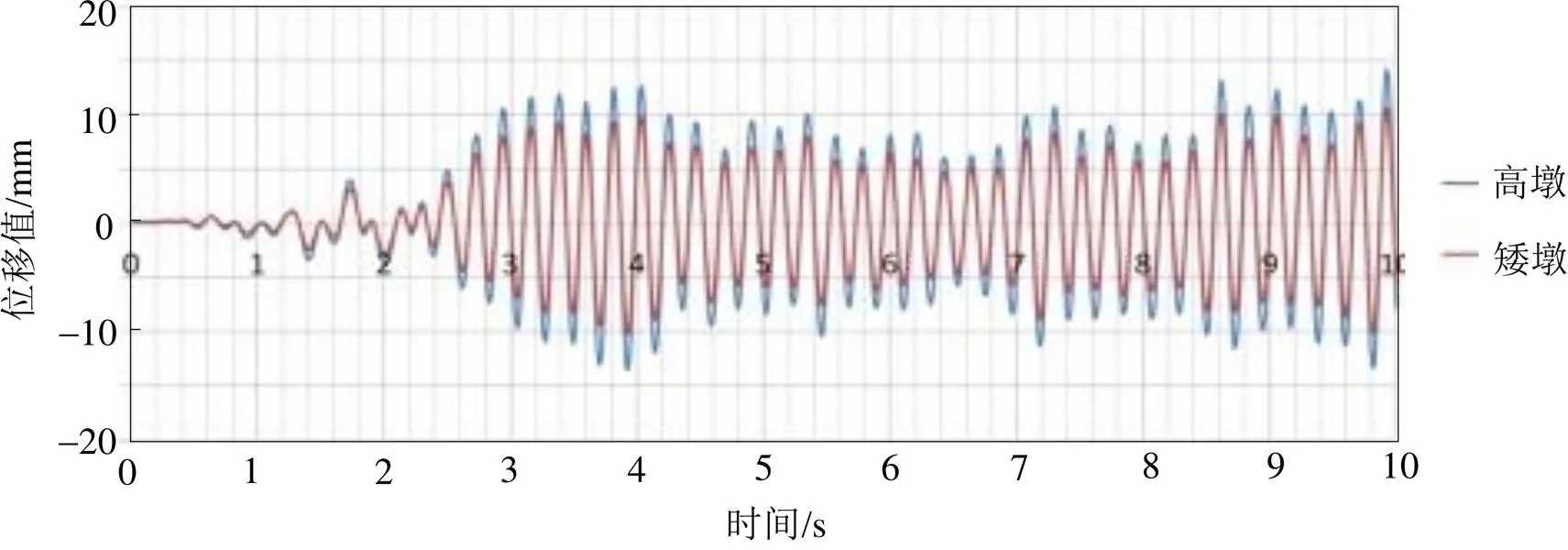
图9 顺桥向墩顶位移时程图

图10 横桥向墩顶位移时程图

6 结论

基于上述对高低墩曲线刚构桥的抗震性能的探讨, 得到以下结论:

(1) 通过该桥在反应谱分析下结构的应力分布图发现桥墩薄弱位置, 墩顶和墩底位置受力较大, 确定了高低墩曲线刚构桥的桥墩控制截面, 并对其内力进一步研究分析;

(2) 墩底最大地震响应弯矩值均发生在顺桥向地震动加载, 于高墩截面顺桥向方向出现, 明显大于横桥向响应弯矩值。但墩顶最大地震响应弯矩值均发生在横桥向地震动加载, 于低墩截面横桥向方向出现。低墩的抗弯能力在横桥向的地震响应中需要更高的需求, 因此对高低墩曲线刚构桥的抗震分析必须考虑横桥向地震效应;

(3) 高、低墩因为墩高的不同, 导致墩身横向刚度差异较大, 且上部结构横向约束较小, 使两墩位移方向和大小相去甚远。这会造成主梁产生扭转, 设计时应结合横向稳定, 提高该类桥梁的抗震性能;

(4) 关于对高低墩曲线刚构桥的力学性能研究较少, 本文基于三维空间有限元模型对该类桥型的地震动响应特性展开研究, 通过对各种地震反应分析计算结果的探讨, 为高低墩曲线刚构桥的抗震设计提供参考。

[1] 何贝贝, 冯仲仁, 陈百奔. 参数变化对高墩弯桥地震响应特性的影响[J]. 中外公路, 2017, 37(3): 164–167.

[2] 连梦磊, 杨德健, 王清龙. 多点激励下大跨高低墩连续拱桥地震响应分析[J]. 天津城建大学学报, 2018, 24(5): 346–350.

[3] 程志友, 钱骥, 陈鑫, 等. 高低墩连续刚构桥的动力特性与抗震分析[J]. 铁道建筑, 2018, 58(7): 18–21.

[4] 游惠敏, 冯仲仁, 陈百奔. 纵向横系梁对双薄壁高低墩连续刚构桥抗震性能影响分析[J]. 公路, 2018, 63(5): 101– 108.

[5] 沈治宇, 赵青. 不同薄壁墩间距的连续刚构桥动力响应分析[J]. 湖南文理学院学报(自然科学版), 2018, 30(1): 80– 84.

[6] 何伟, 刘鹏. 近断层高低墩连续刚构桥抗震分析[J]. 工程抗震与加固改造, 2018, 40(1): 72–75.

[7] 叶列平, 陆新征, 马千里, 等. 混凝土结构抗震非线性分析模型、方法及算例[J]. 工程力学, 2006(z2): 131–140.

[8] 葛俊颖. 桥梁工程软件Midas civil使用指南[M]. 北京: 人民交通出版社, 2013.

[9] 重庆交通科研设计院. 《公路桥梁抗震设计细则》(JTGT B02-01-2008)[S]. 人民交通出版社:82008-9-1: 15114122

[10] 朱慈勉. 结构力学(下册)[M]. 北京: 高等教育出版社, 2016: 8.

[11] 倪国葳, 刘倩, 韩冰, 等. 高墩大跨度刚构桥抗震加固有限元分析[J]. 世界地震工程, 2019, 35(2): 193–202.

Seismic analysis of high and low pier curved rigid frame bridge in high intensity area

Peng Wenyi, Tang Bo

(School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China)

In order to investigate the seismic response characteristics of high-low pier curved rigid-frame bridges in high-intensity areas, a high-low pier curved rigid-frame bridge in Yunnan is selected as the engineering background. The fiber element in the MIDAS software is used to conduct nonlinear dynamic elastoplastic analysis to obtain the bridge's dynamic characteristics and ground motion response. The results show that under the loading of the bridge, the strongest ground motion response appears at the control section of the pier bottom, and the high pier is more severe than the low pier; under the load of the horizontal bridge, the strongest ground motion response appears at the low pier section. The trend of the bending resistance is more sensitive. The lateral thrust stiffness of high and low pier piers is significantly different, and the main beam is twisted laterally during loading.

high intensity; curved rigid frame bridge with high and low piers; finite element; design earthquake; rare earthquake; nonlinear

U 442.5+5

A

1672–6146(2020)03–0070–06

10.3969/j.issn.1672–6146.2020.03.013

彭文毅, 582367673@qq.com。

2019–11–08

湖南省交通科技计划项目(201526)。

(责任编校: 刘刚毅)