机器人系统有限时间自适应迭代学习控制
管海娃
1.浙江工业大学 信息工程学院,杭州 310023
2.温州科技职业学院,浙江 温州 325006
1 引言
迭代学习控制技术适用于有限时间区间上重复作业的控制对象。这种控制技术利用前次或前几次运行结果来修正本次控制输入,只要足够多次的运行,可实现在整个作业区间上的完全跟踪。在实际应用场合,机器人系统经常需要执行重复性工作任务(例如执行搬运、装配等任务的工业机械臂),鉴于机器人运动的重复性特点和迭代学习控制的特性,自1984年提出以来,迭代学习控制技术已被广泛应用于机器人运动控制[1-5]。
近年来,类Lyapunov方法下迭代学习控制技术已经成为研究的热点[6-11]。目前的研究成果主要集中于不确定系统,包括参数化情形和非参数化情形的学习控制,非一致轨迹跟踪问题以及初值问题。文献[12]针对具有时变和时不变参数不确定系统,提出一种新的迭代学习控制方法,能有效地跟踪不同的期望轨迹。文献[13]提出的鲁棒自适应迭代学习控制方法能够处理离散非线性系统中的参数和非参数不确定。文献[14]通过迭代学习控制算法,解决了一类多输入多输出系统的非参数不确定性。文献[15]针对在任意初值和可变轨迹下,研究了一类离散不确定系统的自适应迭代学习控制方法。文献[16]利用障碍Lyapunov函数设计控制器,实现控制过程中的输出约束。文献[17]借助文献[16]的思想,构造二次分式型障碍Lyapunov函数函数,提出实现状态约束的迭代学习控制算法。文献[18]通过自适应迭代学习控制,处理高阶非线性多智能系统的一致跟踪问题。
初始定位是应用迭代学习控制技术的一个必要条件,它要求在每次迭代开始时系统的初值要和期望轨迹的初值一致。大量较早的文献研究机器人系统的迭代学习控制方法,往往假定系统初始误差为零[19-21]。但由于实际精度的限制,初始定位误差难以避免,上述假设很难满足。因此,研究在任意初态下的迭代学习控制算法具有重要的理论与实际意义。针对连续系统的Lyapunov方法,解决初值问题的方案有时变边界层、误差跟踪、有限时间吸引子和初始修正等。文献[22]基于Lyapunov方法研究了迭代学习控制中的五种不同初始条件。文献[23]在非零初始误差条件下,引入时变边界层,构造模糊自适应迭代学习控制器。文献[24]借助初始修正吸引子的概念,提出有限时间迭代学习控制方法,实现在预先指定的区间上零误差跟踪。文献[25]研究在任意初始条件下非线性系统的误差跟踪学习算法。近年来,人们提出重复学习控制方法处理机器人系统的初值问题,这种控制方法在实施时不需要进行定位操作,而以上一周期终点时刻系统状态信息作为下一周期系统的初值。文献[26]针对不确定机器人的轨迹跟踪问题,提出了一种自适应重复学习控制方法。文献[27]通过设计重复学习控制方案,处理时变机器人系统的定常和时变参数不确定性。文献[28]提出一种新的非线性分散重复学习控制,处理非线性机器人系统的轨迹跟踪问题,实现全局渐近收敛。文献[29]构造新型Barrier函数,实现机器人系统位置约束的重复学习控制算法。重复学习控制,回避了迭代学习控制的初始定位问题,但要求参考轨迹是光滑闭合的。针对非零初始误差,文献[30]通过修正参考轨迹,提出机器人系统变轨迹问题的迭代学习控制算法。这种方法,在每次实现时,需要设计起始段轨迹。本文借助初始吸引子概念。以回避这一问题。它在任意初态条件下,实现机器人系统在有限时间内对期望轨迹的完全跟踪问题。
本文通过构造一个含有初始修正项的误差变量,采用Lyapunov-like方法,设计迭代学习控制器处理系统中不确定性,并进行性能分析。所提的方法在任意初始条件下,实现跟踪误差在预先指定区间收敛于零。本文分别针对定常/时变机器人系统,采用未含/含限幅学习机制,保证闭环系统各变量的一致有界性。仿真实例中,以三自由度刨床机械臂系统和二自由度的时变机器人系统,来说明方法的有效性。本文主要由以下几个贡献点:(1)针对非零初始条件,将初始吸引子方法运用于定常/时变机器人系统,实现跟踪误差在预先指定区间收敛于零。(2)本文构造一个修正误差信号,并给出两种新的ζ(t)函数的构造方案,改进了现有的同类设计方案。文中所给出的修正误差构造方案,具有结构简单和实施便捷的特点。
2 问题的描述
2.1 定常机器人系统
考虑下述n自由度刚性定常机器人系统:

其中,q,q̇,q̈∈Rn分别是关节的位置、速度和加速度向量,τ∈Rn是输入力矩向量,D(q)∈Rn×n是惯性矩阵,C(q,q̇)是向心力和哥氏力矩阵,g(q)∈Rn是重力向量。
机器人系统(1)具有如下三个重要的性质:
性质1D(q)是对称正定的矩阵。
性质 2Ḋ(q)-2C(q,q̇)是反对称矩阵。
性质3动态方程(1)可线性参数化成如下形式:
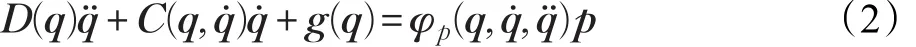
其中,p 是未知的定常参数向量,φp(q,q̇,q̈)是相应的回归矩阵。
2.2 时变机器人系统
在实际情况下,许多机器人系统的载荷会随时间变化,针对时变不确定性,考虑下述时变机器人系统:
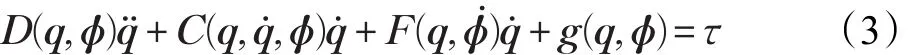
其中,ϕ∈Rϕ是参数向量,D(q,ϕ)∈Rn×n是惯性矩阵,C(q,q̇,ϕ)是向心力和哥氏力矩阵,g(q,ϕ)∈Rn是重力向量,F(q,ϕ)是由于引入时变参数ϕ而增加的相关项,其他量的定义同系统(1)。
时变机器人系统(3)同样具有三个重要的性质:
性质4D(q,ϕ)是对称正定的矩阵。
性质5Ḋ(q,ϕ)-2C(q,q̇,ϕ)-F(q,ϕ̇)是反对称矩阵。
性质6动态方程(3)可线性参数化成如下形式:
D(q,ϕ)q̈+C(q,q̇,ϕ)q̇+F(q,ϕ̇)q̇+g(q,ϕ)=
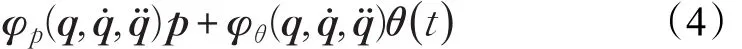
其中,ϕ=[p,θ(t)]T,p是未知的定常参数向量,θ(t)是未知的时变参数向量,φp(q,q̇,q̈)和 φθ(q,q̇,q̈)是相应的回归矩阵。
当系统在区间[ ]0,T 上重复执行任务时,下标k记重复运行次数。给定二阶连续可导的期望轨迹qd()t,定义跟踪误差ek=qd-qk。
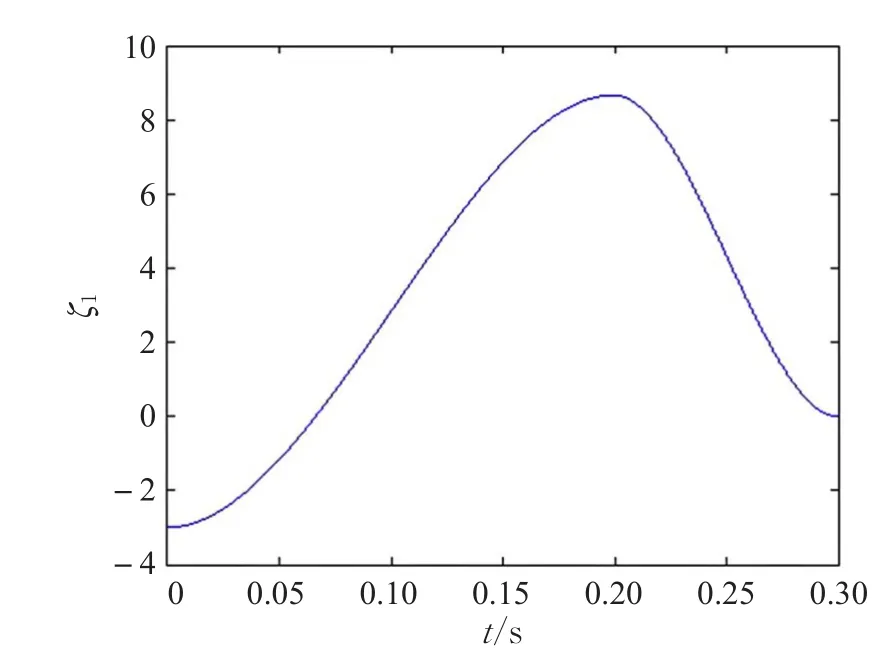
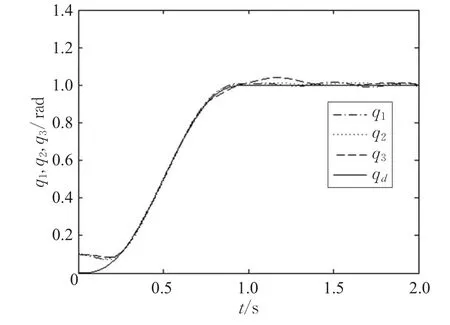
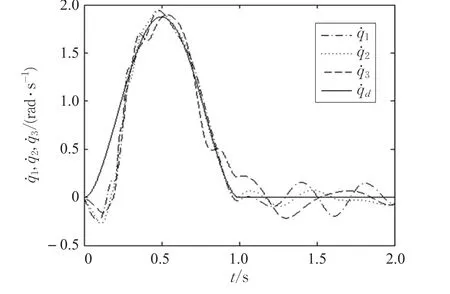
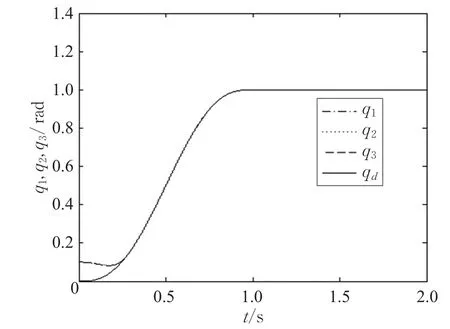
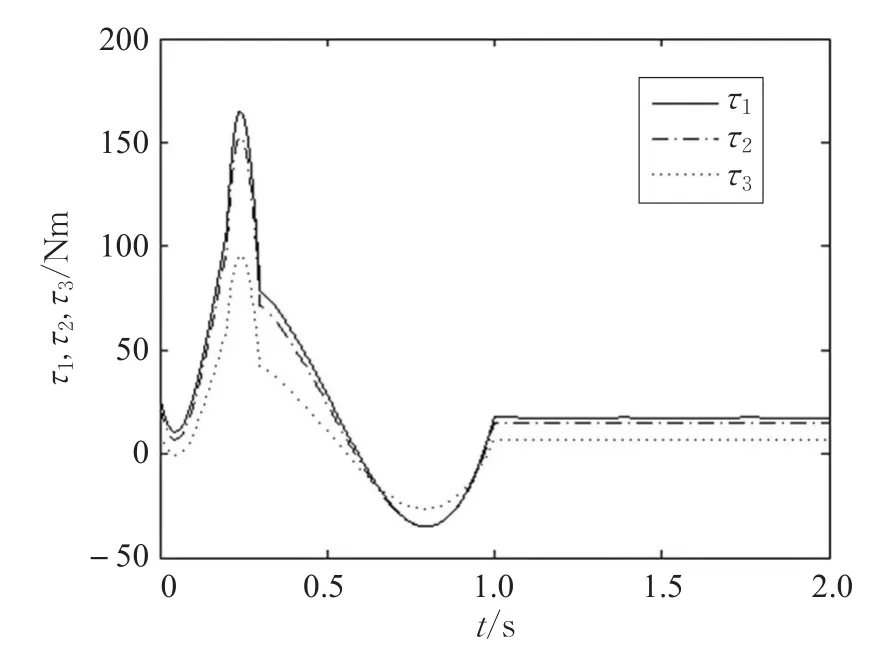
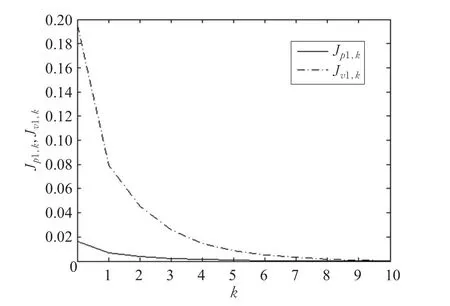
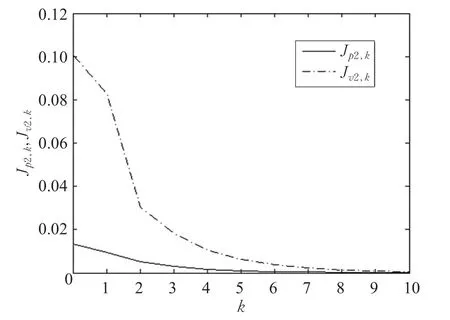
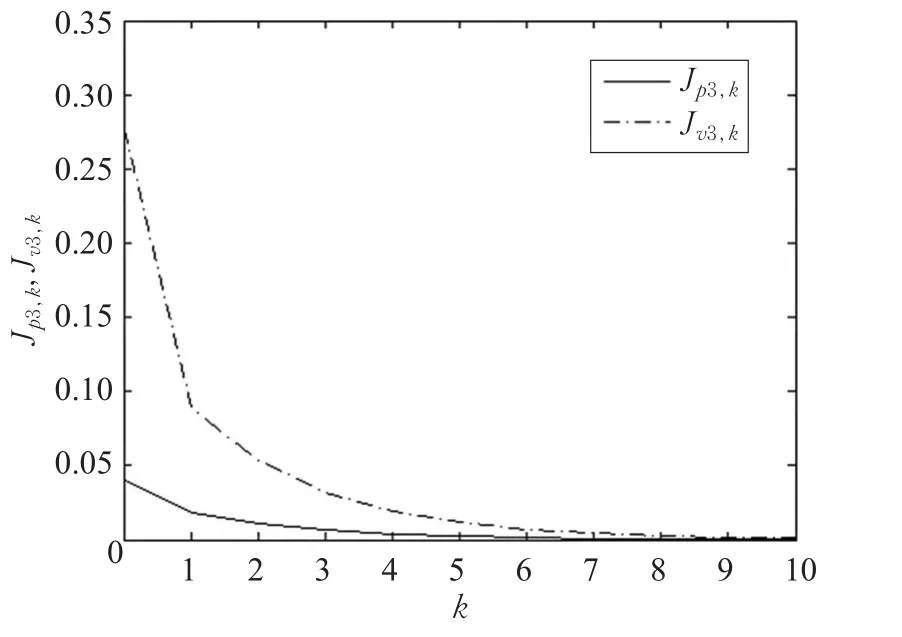
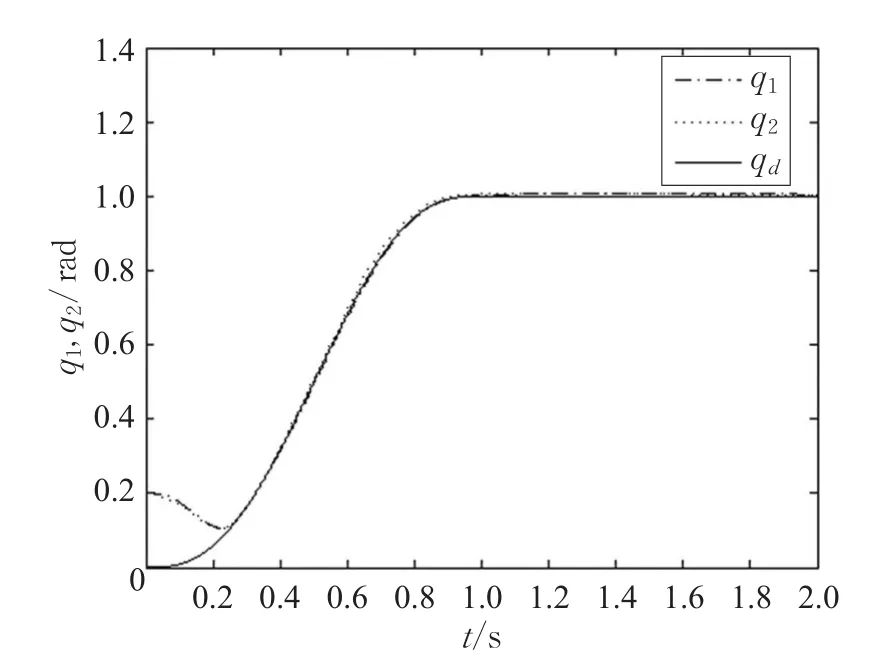
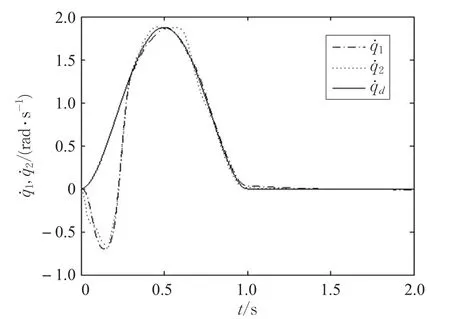
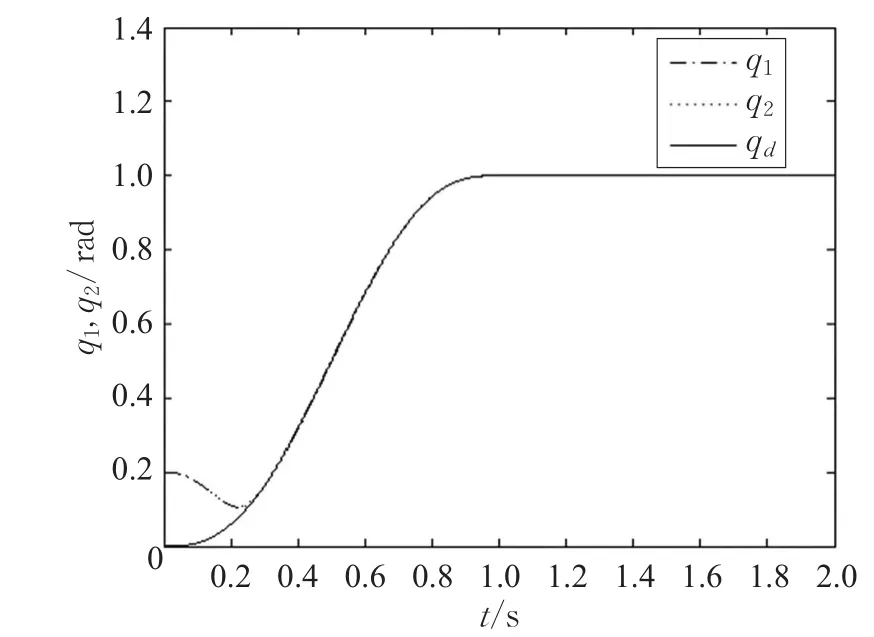
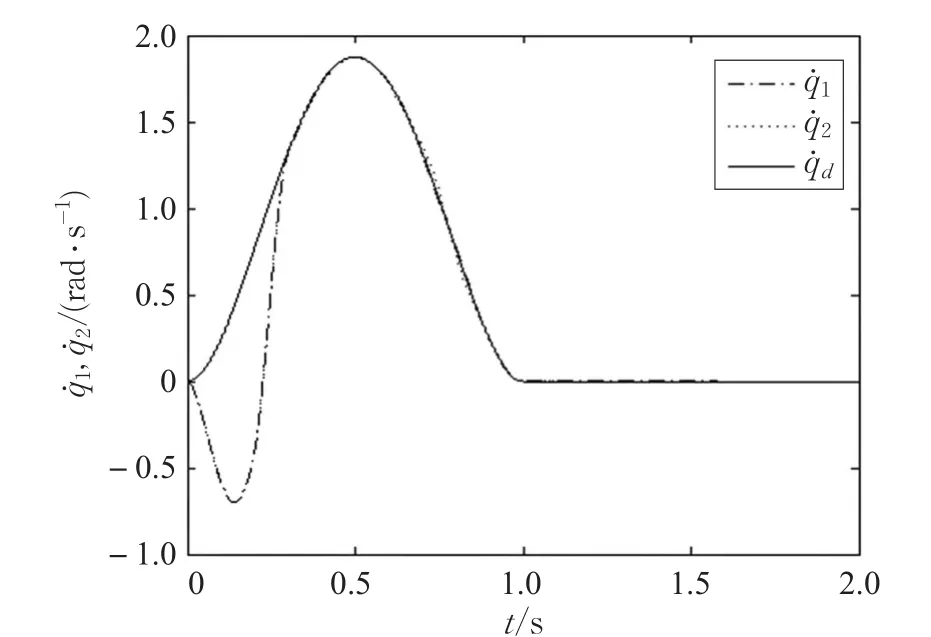
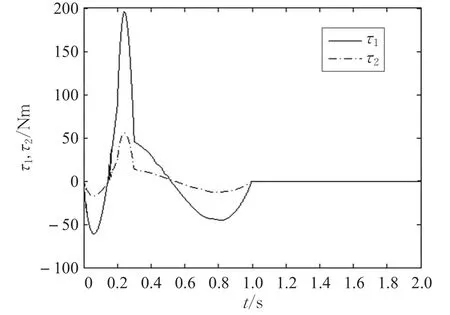
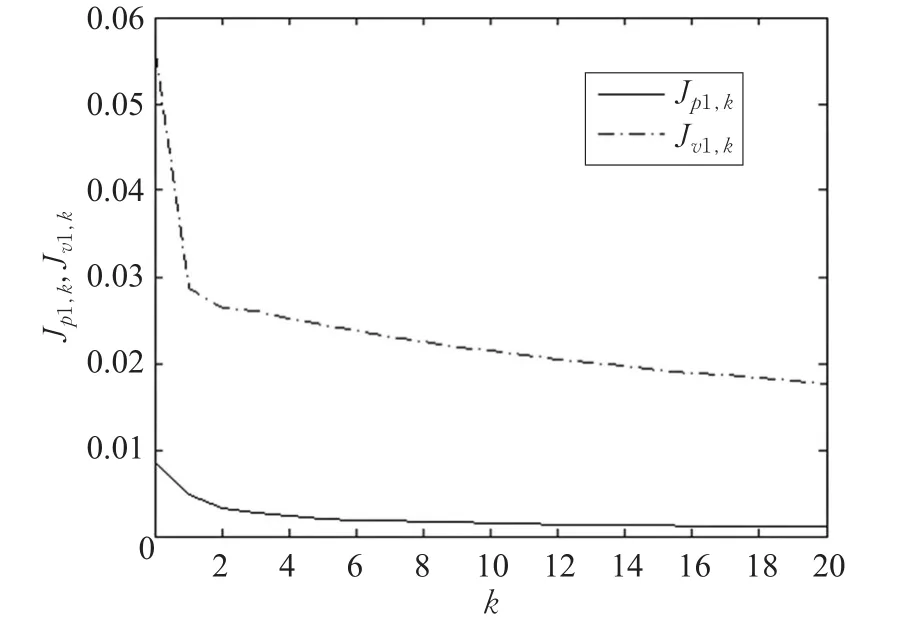
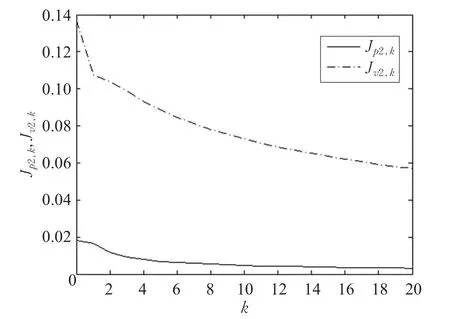
本文的控制任务是,在任意初态的情形下,即ek(0)≠0,分别针对定常/时变机器人系统设计迭代学习控制器τk,使得跟踪误差ek能够在预先设定的区间上实现完全跟踪(0<Δ 对于微分方程:其中,α>0,其解可表示为: 方程(5)有唯一的吸引子 χ=0。显然,对于非零χ0,这是无穷时间吸引子,当时间趋于无穷大时,χ收敛于该吸引子,即在迭代学习控制器的设计中,一种更诱人的控制性能是有限时间收敛性。 定义1[24]对于微分方程: 其中,α>0,如果存在初始修正作用r=r(χ0,t),使得对于给定的Δ>0,有: 那么,称 χ=0为 χ̇=-αχ-r的初始修正吸引子。 下面给出一种初始修正作用: 式中,ζ(t)是关于t的函数,满足: 由于引入初始修正作用(8),微分方程(7)的解为: 由上式可知,方程的解具有有限时间收敛性。对式(10)求导,可得: 由 ζ- 函数的定义可知,ζ(Δ)=0 ,可使得 χ̇(Δ)=0 ,因此,χ(t)在Δ时刻可光滑对接。 鉴于上述初始修正吸引子的概念,本文针对非零初始误差情形,为了实现有限时间完全跟踪性能,构造修正误差变量: 其中,c>0是可调整的参数,rk是为处理非零初态条件而引入的修正作用,其可表示为: 其中,ek(0)是初始误差。为了设计迭代学习控制器,选取的ζ(t)在满足式(9)的前提下,要使得下式恒成立: 注2本文系统初始误差ek(0)≠0,不满足常规迭代学习控制算法的要求。为了解决这个问题,构造修正误差变量σk(t),并要满足σk(0)=0。 当ėk(0)=0时,本文给出一种ζ(t)函数的构造方案: 其中,0 当c=3,d=0.2,Δ=0.3,ζ1(t)函数图像如图1。 图1 ζ1(t)函数 ζ(t)函数的构造方案有很多种,类似的,本文给出另一种ζ(t)函数:其中,0 注3现有的几种ζ(t)函数,在t=0,t=Δ处不连续,或在t=Δ处不可导。本文给出两种新的ζ(t)函数的构造方案,由式(15)、(16)可以看出,构造的两种 ζ(t)函数在(0 ,T ]上是连续可微的,相应的,rk在(0 ,T]上是连续可微的。由式(12)可知σk在[0 , T]上也是连续可微的。 若当σk(t)=0,t∈[0 , T ]成立,式(12)可写成: 由定义1可知,ek(t)=0,t∈[Δ ,T ],并且可得 ėk(t)=0,t∈[Δ ,T]。 由上面的分析可得,设计迭代学习控制器,经过足够多次迭代后,若能实现在整个作业区间[0 , T]上,σk(t)=0,即可实现在[Δ ,T ],ek(t)=0 和 ėk(t)=0 。这是下一章控制器设计的策略所在。 引入新的变量: 修正误差变量可转换为: 建立修正误差变量的动态方程: 将式(1)代入式(20),并利用性质3可得: 其中,Yp(qk,q̇k,q̇σ,k,q̈σ,k)是相应的相容矩阵,记为Yp,k。 为设计迭代学习控制器,考虑正定函数: 对Vk求导: 通过上面的推导,本文可采取如下控制器: 其中,p̂k是对 p的估计,p̂k的更新律由下式给出: 其中,Q,Γ是对角正定矩阵。应用力矩输入式(24),并结合性质2,式(23)可写成: 为分析闭环系统的收敛性和稳定性,考虑下述Lyapunov-like函数: 容易得到Vk()0=0。Lk在第k次的迭代差分为: 由分部积分,可得: 将式(26)、(29)代入式(28)得: 应用参数更新律(25),式(30)可写成: 由于: 那么: 由于 p̂k(0)=p̂k-1(T),再令 t=T ,得到: 依据式(34),容易证明下述定理。 定理1对于在任意初态情形下的机器人系统(1),采用力矩输入(24),以及参数更新律(25),可以保证: (1)闭环系统中的所有变量在[ ]0,T上一致有界。 (2)当k→∞时,跟踪误差在[ ]Δ,T 上一致收敛于零,即: 证明 首先对L0(t)求导: 因此,Lk(t)在上是有界的,由式(27)可知Vk(t),p̂k(t)和 σk(t)在上都是有界的。由σk的有界性可得 ek和 ėk在上是有界的。由qd,q̇d和rk的有界性,可得上也是有界的。进而,由 式(24),可知 τk(t)在上也是有界的。因此,闭环系统的所有信号都是有界的。 为证明误差σk(t)一致收敛,对式(34)进行累加: 由Lk(T)≥0和L0(T)的有界性,得到: 同上一章,引入变量 q̇σ,k,q̈σ,k,利用时变机器人系统的性质6,建立修正误差变量的动态方程: 给出如下控制器: 其中,p̂k和 θ̂k分别是对 p 和 θ 的估计,p̂k和 θ̂k的更新律由如下式子给出: 定理2对于在任意初态情形下的时变机器人系统(3),采用力矩输入(37)以及参数更新律(38)、(39),可以保证: 其中,Q,Γ1和Γ2是对角正定矩阵。sat为饱和函数,本文sat(⋅)定义为,对于a∈R: (2)有界性证明。首先对L0(t)求导: 由 θ 和 θˉ-1的有界性可知是有界的,类似于定理1的有界性证明过程,可是有界的,进而可得上是都是有界的。由式(37),可知τk(t)在[ ]0,T上是有界的,因此闭环系统的所有信号都是有界的。进一步可得上一致收敛于零。由前面的分析可知,上一致收敛于零。 例1考虑如下三自由度的机械臂系统[31],其模型为: 其中,D(q)=[Dij],C(q,q̇)=[Cij],g(q)=[gi],具体各值具体各值可参考文献[31],q1,q2,q3分别表示各关节的位置,q̇1,q̇2,q̇3分别表示各关节的速度,l1,l2,l3分别是各关节长度,m1,m2,m3分别是各关节的重量,i1,i2和i3是三个和惯性有关的定常参数,g表示重力加速度。对机械臂系统进行参数化,有p=[m1,m2,m3,i1,i2,i3]T,Yp是相应的相容矩阵,给定如下: 采用式(13)所示的初始修正作用,其中,ζ(t)选取为式(15)的形式,其中参数取值为:T=2 s,Δ=0.3 s,d=0.2 s,t1=1 s,c=2。 采用力矩输入式(24)以及参数更新律式(25)。参数取值为Q=diag[8 , 6,6],Γ=diag[17]。其他数值取为: 仿真结果由图2~图9所示。由图2~图5可看出,在非零初始误差下,引入初始修正作用,设计的迭代学习控制器,经过足够多次迭代,可实现关节的位置和速度轨迹在时间区间[0 . 3,2]上完全跟踪上相应的期望轨迹。图6给出了在k=10时的关节力矩输入。图7表示关节1的两个性能指标随迭代次数的变化情况,其定义为:分别表示在[Δ ,T ]上关节1的位置和速度误差绝对值的最大值。图8表示关节2的两个性能指标随迭代次数的变化情况,定义为:分别表示在 [Δ ,T ]上关节2的位置和速度误差绝对值的最大值。图9表示关节3的两个性能指标随迭代次数的变化情况,定义为分别表示在[Δ ,T]上关节3的位置和速度误差绝对值的最大值。 例2考虑二自由度的刚性机械臂系统[27],假设机械臂的载荷是时变的,其系统模型为: 图2 当k=0时,系统位置q和期望轨迹qd 图3 当k=0时,系统速度q̇和期望轨迹q̇d 图4 当k=10时,系统位置q和期望轨迹qd 图5 当k=10时,系统速度q̇和期望轨迹q̇d 图6 当k=10时,力矩输入τ 图7 指标Jp1,k和Jv1,k 图8 指标Jp2,k和Jv2,k 图9 指标Jp3,k和Jv3,k 期望轨迹设计同例1。采用式(13)所示的初始修正作用,其中,ζ(t)选取为式(15)的形式,其中参数取值为:T=2 s,Δ=0.3 s,d=0.2 s,c=2。采用力矩输入式(37)和参数更新律式(38)、(39)。参数取值为Q=diag[2 0,10],其他数值取为: 由图10和图11分别表示k=0时,机械臂关节1和关节2的位置和速度轨迹。迭代20次后,仿真结果由图12~16所示。由图12和图13可看出,经过足够多次迭代,关节的位置和速度轨迹在时间区间[ ]0.3,2上完全跟踪上相应的期望轨迹。关节力矩输入在第20次迭代期间的取值情况见图14。图15表示关节1的两个性能指标Jp1,k和Jv1,k随迭代次数的变化情况。图16表示关节2的两个性能指标Jp2,k和Jv2,k随迭代次数的变化情况。指标Jp1,k、Jv1,k、Jp2,k和Jv2,k的定义同例1。 图10 当k=0时,系统位置q和期望轨迹qd 图11 当k=0时,系统速度q̇和期望轨迹q̇d 图12 当k=20时,系统位置q和期望轨迹qd 图13 当k=20时,系统速度q̇和期望轨迹q̇d 图14 力矩输入τ 图15 指标Jp1,k和Jv1,k 图16 指标Jp2,k和Jv2,k 本文提出定常/时变机器人系统的有限时间迭代学习控制方法,解决在任意初态下的完全跟踪问题。通过构造修正误差变量,利用Lyapunov-like方法,分别设计迭代学习控制器处理系统中的不确定性,经过足够多次迭代后,修正误差变量在整个作业区间上一致收敛于零。借助初始修正作用,实现跟踪误差在预先指定区间上的完全跟踪。最后的仿真实验验证了这种学习控制方法的有效性。3 修正误差信号的构造


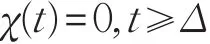


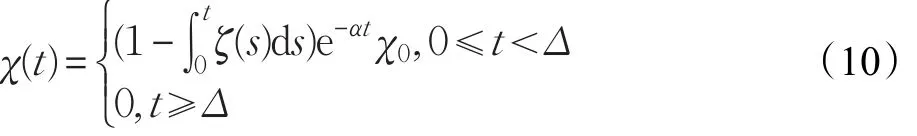
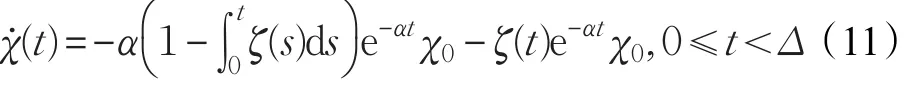



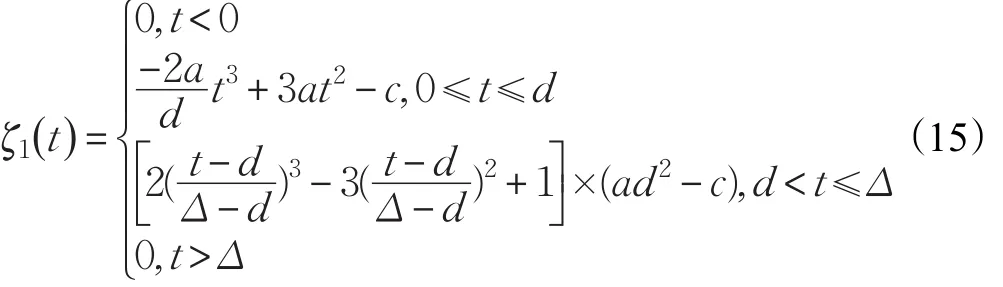

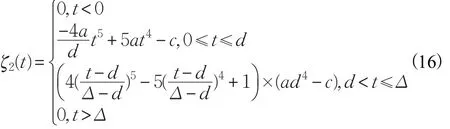
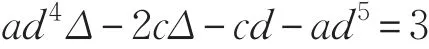

4 定常机器人系统的控制器设计与性能分析


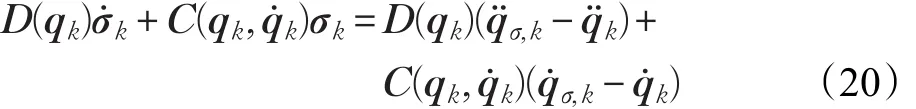
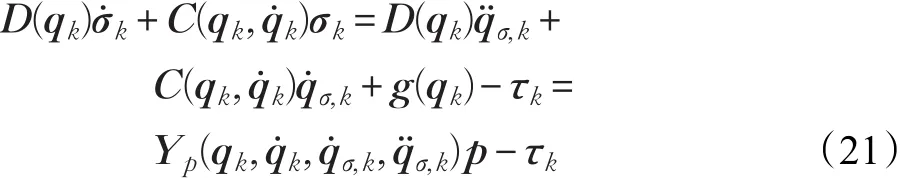

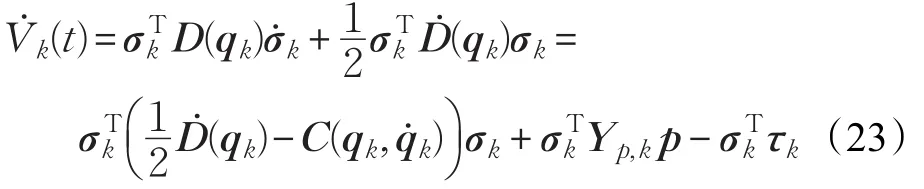

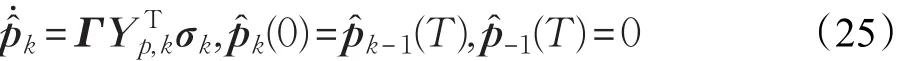

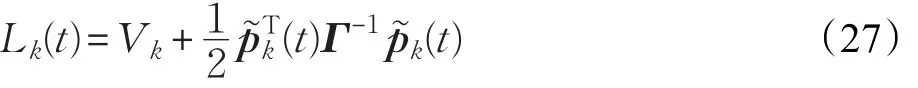
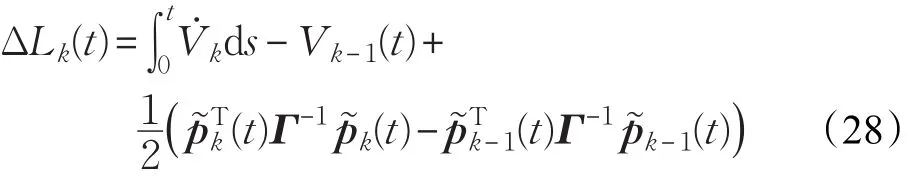
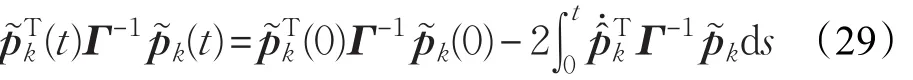
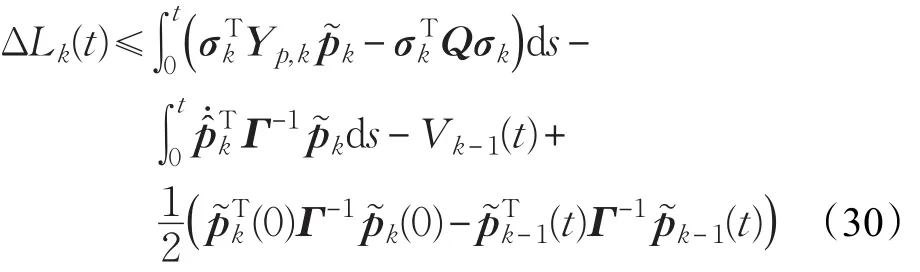
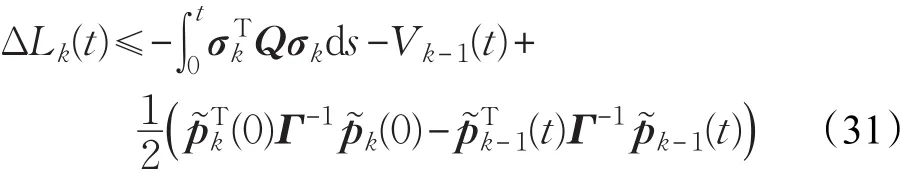
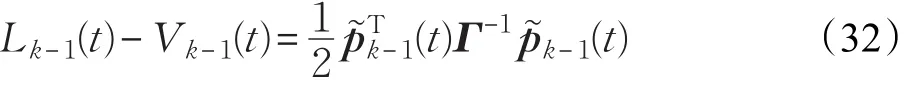
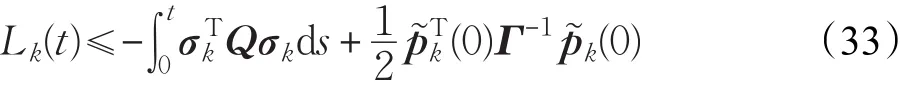

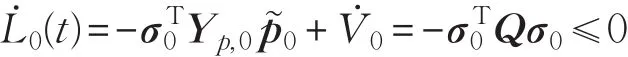
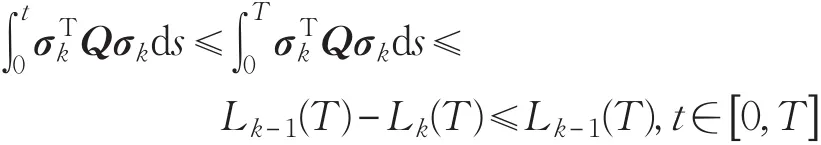
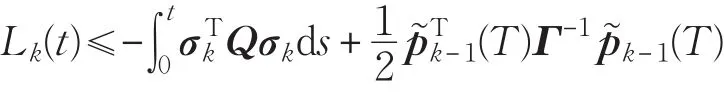
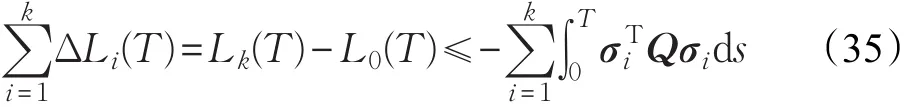
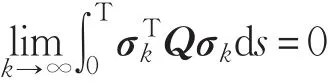
5 时变机器人系统的控制器设计与性能分析
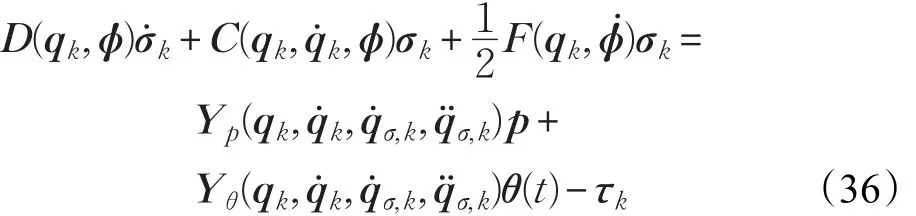
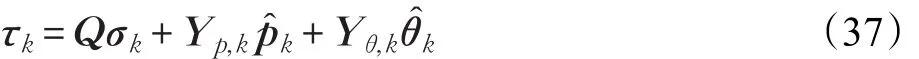
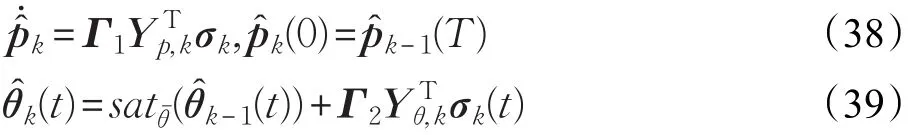
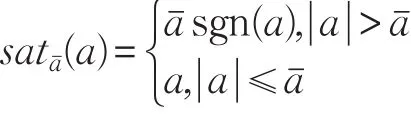


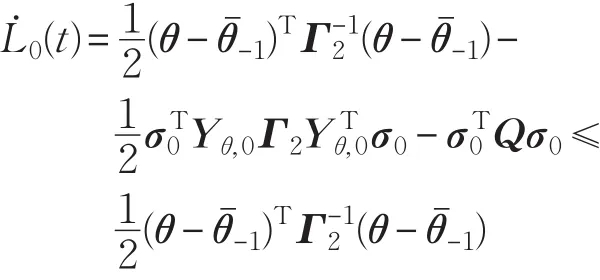
6 仿真算例

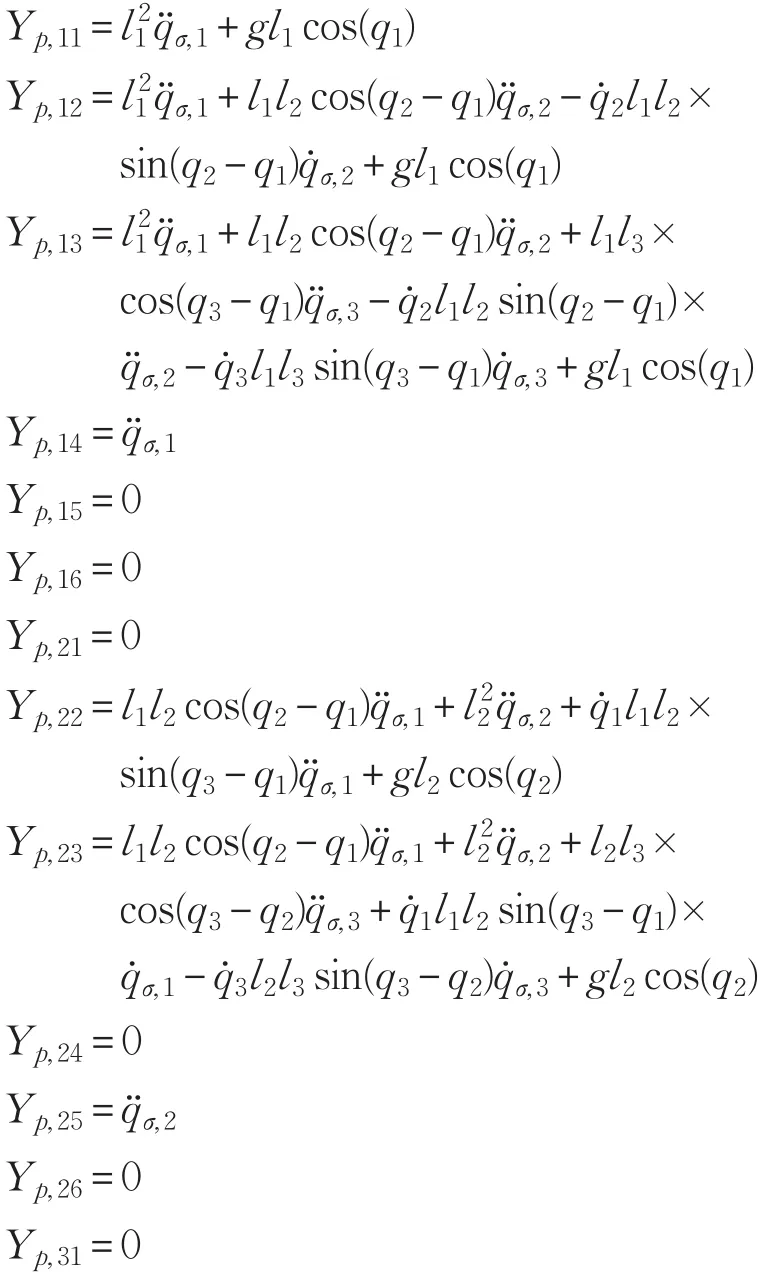
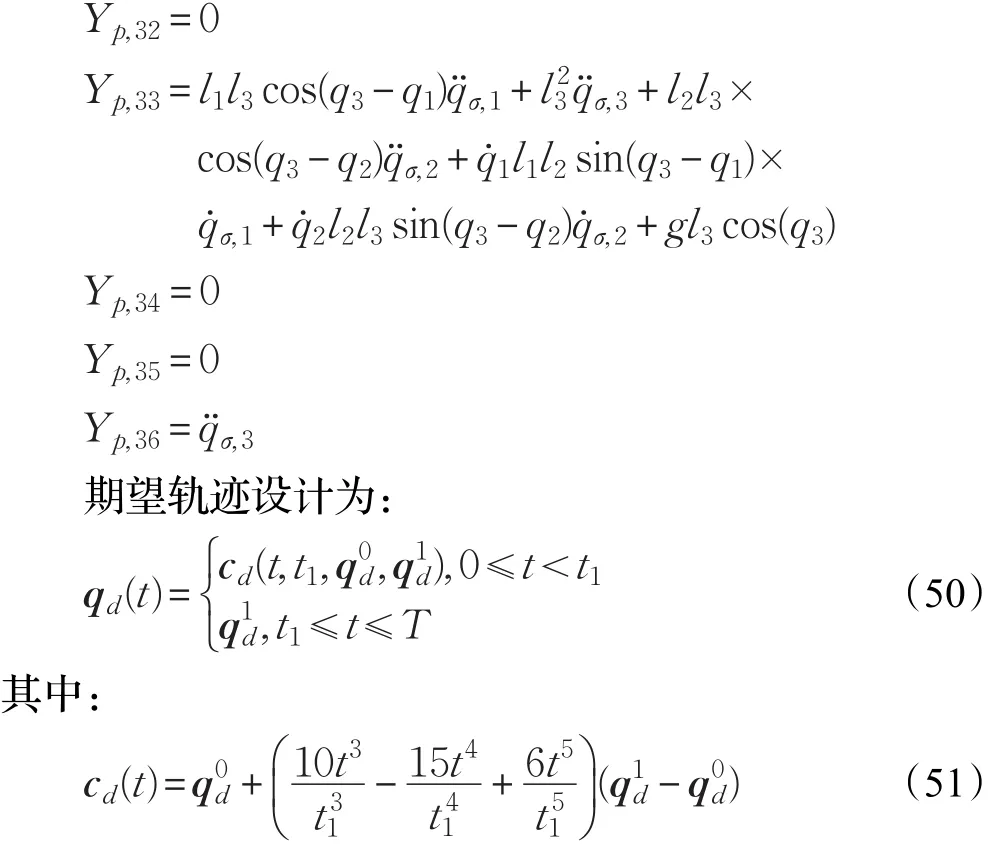
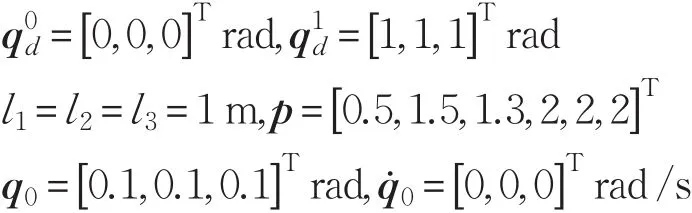
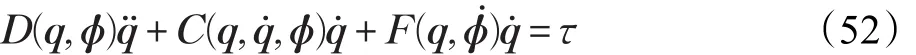

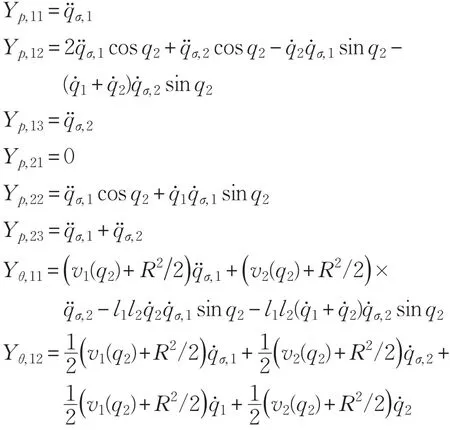
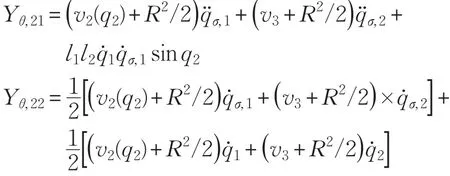
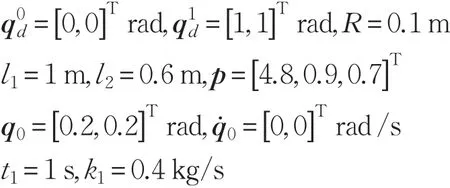
7 结束语

