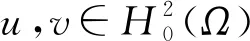具强阻尼项的四阶弱耦合双曲方程组解爆破时间的下界估计
陈洁姝, 金 鑫
(吉林大学 数学学院, 长春 130012)
0 引 言
对非线性双曲方程解的生命跨度分析研究目前已得到广泛关注. 对于二阶双曲方程, 曹春玲等[1]通过构造带阻尼项的控制函数, 得到了一类具超临界源的非线性黏弹性双曲方程解的爆破时间下界估计; 孙爱慧等[2]给出了具非线性阻尼项和源项的双曲方程解爆破时间的下界估计; 王雪等[3]通过构造具耗散项的新控制函数, 得到了具超临界源非线性双曲方程解爆破时间的下界估计. 对于四阶双曲方程组, 文献[4]利用能量估计和Sobolev嵌入定理讨论了一类四阶半线性波动方程初边值问题解发生爆破的充分条件和爆破时间的下界估计; 文献[5]将文献[1]的结果推广到了半线性双曲Petrovsky方程组; 文献[6-8]进一步研究了这类问题. 由于源项导致双曲方程解在有限时间内发生爆破, 而阻尼项导致双曲方程解趋于稳定. 因此, 对于方程组, 不仅要考虑阻尼项和源项的竞争影响, 而且还要考虑耦合项给这类问题带来的很多困难, 例如, 如何定义能量泛函、 如何克服耦合项带来的交叉影响等. 受上述工作的启发, 本文主要考虑如下四阶非线性双曲型方程组解的爆破行为:

(1)
其中:Ω是N(N≤3)中具有光滑边界的有界区域;p>2;bi(t)(i=1,2)是正的连续函数.
本文的目的是研究问题(1)爆破解的爆破时间t*的估计, 通过构造合适的控制函数, 运用能量估计和Sobolev嵌入不等式, 对控制函数建立一性微分不等式, 进而给出爆破时间t*的一个下界估计. 为方便叙述, 设
定义1如果

(2)
则称问题(1)的解在t*时刻爆破.
引理1[6]设Ω是N(N≤3)空间的有界区域, 2≤q<+∞, 则对任意的存在一个依赖q和Ω的常数C, 使得
‖ω‖q≤C‖Δω‖2.
(3)
引理2[4]设Ω是N(N=2或N=3)空间中边界光滑的有界区域,q>1为常数, 则有正常数
使得
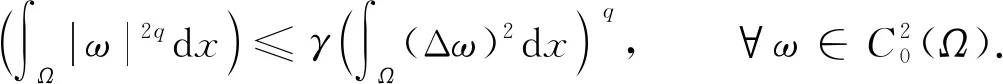
(4)
类似文献[6]中引理2.4的证明, 有:


(5)
1 主要结果
先对能量泛函E(t)建立一个微分不等式.
定理1设(u,v)是问题(1)的解, 则E(t)满足
E′(t)≤a(t)E(t)+b(t)Ep-1(t),
(6)
其中:a(t)=2+max{b1(t),b2(t)};b(t)=max{b1(t),b2(t)}C2(p-1),C为嵌入正常数.
证明: 证明可分如下三步完成.
1) 定义
则E(t)=E1(t)+E2(t). 进一步, 直接计算可得
2) 估计J1,J2,J3的值. 首先, 估计J1:
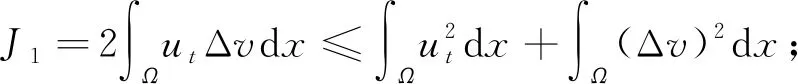
(8)
其次, 估计J2:
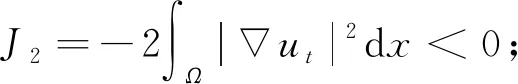
(9)
最后, 估计J3: 根据基本不等式和引理1, 可知
根据式(7)~(10), 可得

(11)
同理可证
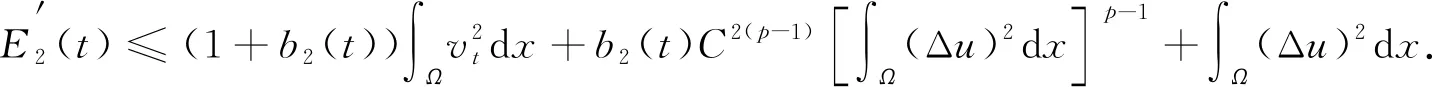
(12)
3) 对于i=1,2, 令g(t)=max{b1(t),b2(t)}, 代入式(11),(12), 有
其中:a(t)=2+g(t);b(t)=g(t)C2(p-1). 证毕.
下面给出爆破时间t*的下界估计.
定理2假设定理1的所有条件成立, 且式(2)成立, 则爆破时间t*满足

(14)
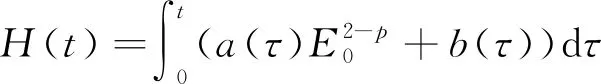
证明: 根据定理1和引理3, 得

令t→t*, 得式(14). 证毕.
推论1假设(u,v)是问题(1)的解, 且bi(t)为常数, 则

(15)
其中:a(t)=2+max{b1,b2};b(t)=max{b1,b2}C2(p-1).
证明: 由定理1得
E′(t)≤aE(t)+bEp-1(t),
则

(16)
将式(16)左右两端同时乘(2-p)ea(p-2)t得
(E2-p(t))′ea(p-2)t+a(p-2)ea(p-2)t≥b(2-p)ea(p-2)t,
(17)
对式(17)从0到t积分, 得
令t→t*, 得式(15).