测量误差分析及数据处理若干要点系列论文（三）——随机性分布统示法推荐应用

林洪桦

特约论文

测量误差分析及数据处理若干要点系列论文（三）——随机性分布统示法推荐应用

林洪桦

（北京理工大学，北京 100081）

阐述现代数据处理中随机性分布统示法应用，分析小样本数据处理难点与对策，详细描述分布统示法的矩估计方法、分布统示法的分位数估计方法、高斯混合模型用于粒子滤波等方法应有的观念、对策与基本方法、步骤及应予关注的问题等。

数据处理；数学模型；误差；统示法

在文献[1]中，笔者阐述了现代数据处理基本观念，包括数据处理目标、依据、实质、现实问题的性质和随机性分布，并根据数据处理对策，对现代数据处理归结出“实、佳、智、验”四字要诀。在文献[2]中，笔者阐述了现代数据处理中随机性分布统示法的必要性以及表示方法。数据处理实质在于按样本数据推测其待求总体信息，依据可靠先验信息十分必要，须辅以对先验信息的处理，其中重中之重在于处理现实的随机性分布问题。本文延续文献[2]，在非高斯性为常态观念下，论述运用随机性分布统示法处理概率分布模式的实用统计处理方法。

1 随机性分布统示法应用概述

传统的误差分析多基于误差呈正态分布的假定。实际上，这样的假定经常并不成立，有些起决定性因素的误差呈均匀分布、瑞利（Rayleigh）分布或反正弦分布等非正态分布，其与一些次要因素的误差合成后，经常表现为一种非典型的概率分布。如齿轮测量、雷达回波、水声信号，生物与医学、社会学与经济学中的测量数据等更常遇到非典型的概率分布，现统称为非高斯分布。实际上，以往并非不认为非高斯性误差为常态，但对其没有实用处理方法。当前已有非高斯性数据实用处理方法，且仍在不断发展完善中，可见分布统示法值得提倡应用，尤其有必要探讨分布形态覆盖面广，且简捷有效的小样本数据处理方法。

2 小样本数据处理难点与对策

文献[1]总结：大多数现实数据宜按小样本处理。小样本数据处理的特点：1）本质特征在于含有总体信息较少，同一总体的小样本分布并不相同，不同总体的小样本分布可能类同，难以推断其总体分布；2）小样本分布不对称，难以体现出其总体对称性；3）小样本特征量欠稳定，同一总体的小样本矩或分位数不尽相同，难以推断其总体特征量及待求的总体特性。

为得出实且准的待求总体特性处理结果，需拟定合适的小样本数据处理对策。文献[1]、文献[2]根据现代数据处理对策归结出四字要诀“实、佳、智、验”，且大体上对应4方面要素：模型、准则、算法、验证。现从其中归纳出如下具体对策：

总原则为从特殊到特殊的转导型推理原则，即按所掌握的有限信息直接估计、预测现实问题待求的结果；

1）在模型化上，在概率分布模式未掌握确切信息时运用统示法，并按分布统示法优先，需覆盖拖尾分布时用分布统示法，需覆盖多峰型分布时才选用混合分布统示法的次序建模策略；

2）以样本统计特征量（样本前四阶矩或分位数等）为主，且辅以可靠先验信息；

3）充分利用统示分布参数，如按样本前四阶矩估计统示分布参数，按样本分位数估计统示分布参数，进而确定待求总体特性，以往刻意地求出小样本所属的典型概率分布毫无实际意义；

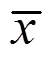
5）可用自助（Bootstrap）法扩展样本所含有总体信息，即运用统示法要求样本容量大才够准，采用自助法对原样本{x,= 1,…,}进行重新独立随机抽样，获得再生大量自助样本= [x],1,2,…,= 20，借其估计前四阶矩或分位数等可多含些总体信息，使估计的结果更准确可靠[3]。

在做数据处理对策之前，首先，进行一些必要的数据预处理：观察数据图（如坐标图、直方图等）、分析特征量、检验异常值、检验对称性、检验趋势性和周期性；然后，通过理论分析、实验结果、技术资料以及主观经验等搜集先验信息；最后，汇集便于初步拟定数据处理方案。

3 β分布统示法的矩估计方法

分布统示法已应用多年，详见文献[3]~文献[5]。由文献[2]表1可知：分布统示法优先应用，且宜运用矩估计。设样本数据为{x}，按上述小样本数据处理对策拟出分布统示法的矩估计方法如下：

2）检测、排除异常数据和显著系统误差，推荐采用文献[3]中式(7.5.3)或式(7.5.4)作为初判，若置信概率(+1)，样本容量≥ 20，则

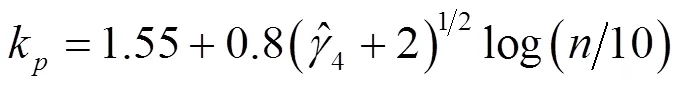
系统误差主要应排除变量系统误差，通过检验数据随机性（符号检验、游程检验、秩相关检验等）即可发现是否存在变量系统误差；排除变量系统误差主要依靠专业技术，可辅以回归分析；

*必要时，如< 20，可采用自助法借自助样本估计前四阶矩[3]：

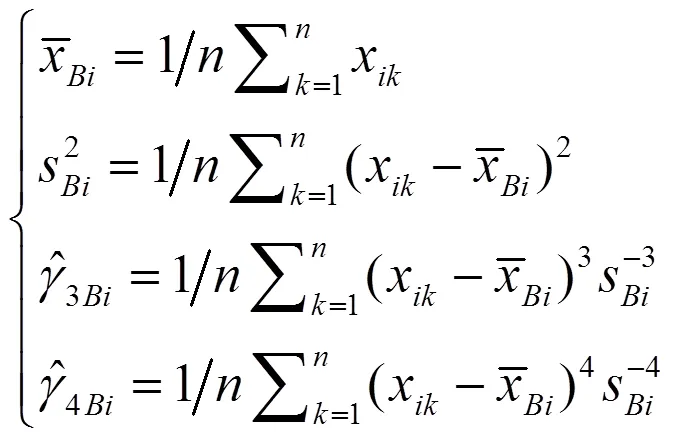
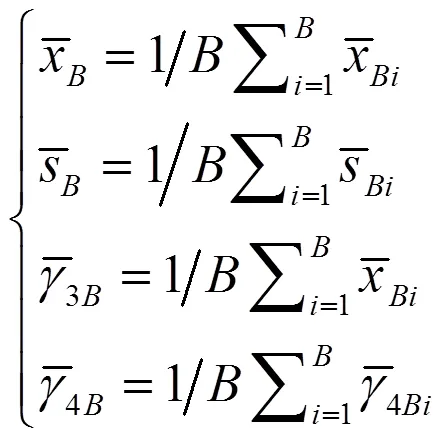
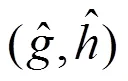
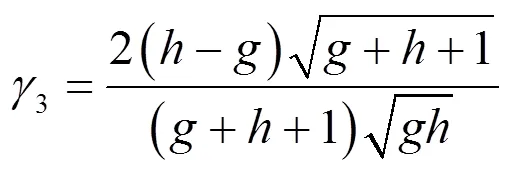
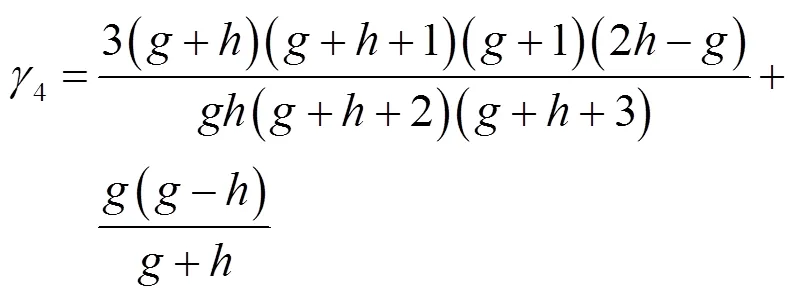
7）估计非对称分布界限，

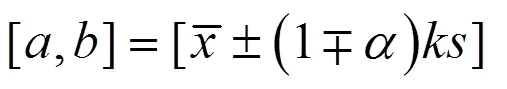
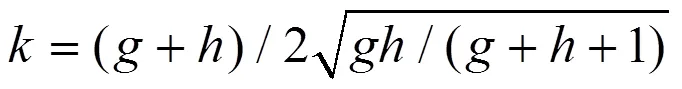
【示例1】测长仪重复20次实测数据为： 150.14, 150.04, 149.97, 150.08, 149.93, 149.99, 150.13, 150.09, 149.89, 150.01, 149.99, 150.04, 150.02, 149.94, 150.19, 149.93, 150.09, 149.83, 150.03, 150.07(mm)。

【示例2】原始数据(= 30)：4.4, 4.9, 4.5, 4.4, 4.6, 4.5, 4.6, 4.3, 4.2, 4.4, 4.3, 4.5, 4.6, 4.2, 4.3, 4.8, 4.8, 4.2, 4.2, 5.3, 4.6, 4.6, 4.5, 4.9, 4.1, 4.5, 4.4, 4.7, 4.2, 4.8 (μm)。

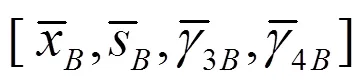
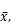
注：该例以往基于正态性数据处理结果，原始数据中5.3判为异常值而弃之。

4 λ分布统示法的分位数估计方法

由文献[2]可知：现实问题用到拖尾型概率分布时宜应用分布统示法，如寿命、磨损等专业领域。小样本下应用分布统示法，实际上就是按样本数据确定分布参数 (1,2,3,4)，因其更宜用分位数形式表述，且前四阶矩较分位数与 (1,2,3,4) 的关系更为复杂，故运用样本分位数估计统示分布参数的方法（尽管也能应用矩估计法）[7]。

以常量测量下按样本数据求其总体分布范围为例，可归纳出分布统示法具体数据处理方法及步骤。

1）预处理

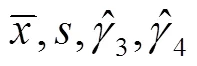
②检测异常数据：一般采用文献[3]中式(7.5.4)作为初判，即粗差e判别式为

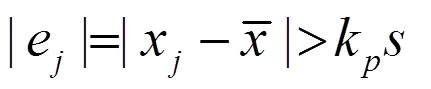
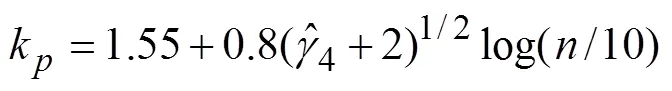
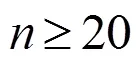
用样本分位数估计时，也可采用文献[3]中具有稳健性的式(7.5.16)作为初判，即异常数据判别式为

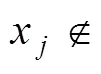
式中，1.5由正态性导出，可另用非高斯性范围。

③排除变量系统误差：如前述，通过检验数据随机性即可发现是否存在变量系统误差；排除变量系统误差主要依靠专业技术，可辅以回归分析。

2）原数据的分位数估计

对原数据统计其顺序统计量为(1),(2), …,(n)，则样本的分位数估计为

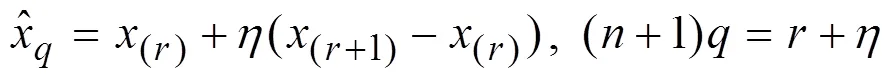
式中，为正整数；为余数。

按文献[2]中表2，分位数特征量的4式估计分别为

且取= (0.05, 0.10, 0.15, 0.20, 0.25, 0.50, 0.75, 0.80, 0.85, 0.90, 0.95)。

3）自助法估计分位数

对原数据生成自助样本x1,x2,…,x，1,2,…,，按式(2)同样方法估计自助样本分位数，即

1,2,…,

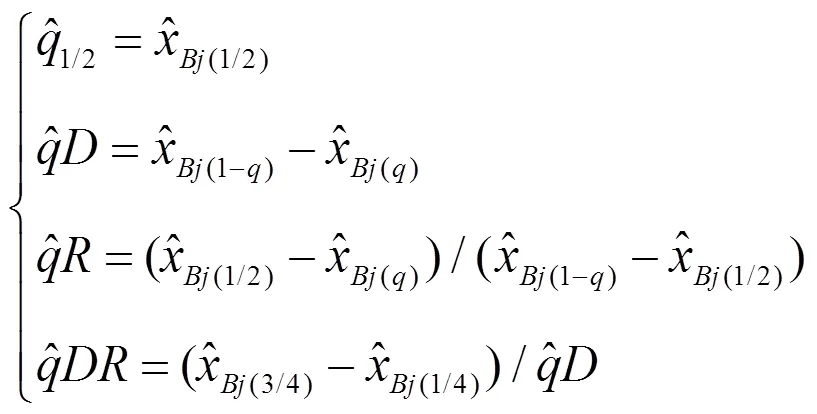
且取= (0.05, 0.10, 0.15, 0.20, 0.25, 0.50, 0.75, 0.80, 0.85, 0.90, 0.95)。

4）对称性处理优先

估计对称分布参数：

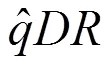
②估计(1,2)：同理利用文献[2]表2相应的分位数特征量公式，可得

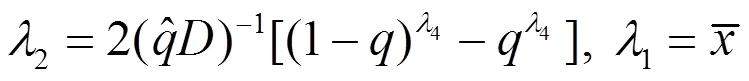
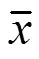
5）估计一般分布参数

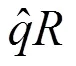
②估计(1,2)：按中位数和分位差公式，可得

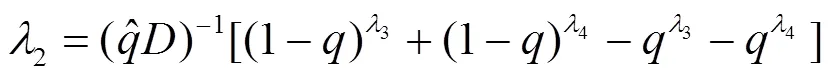
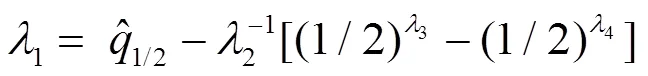
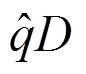
6）估计总体分布范围

估计(1,2,3,4)后，按文献[2]表2中分位数函数式，令= 0，= 1算出总体分布范围[,] = [(0),(1)]。

【示例3】：示例2的数据按上述分布统示法的数据处理方法及其步骤估计其总体分布范围，结果如下：

分位数关系：（中位数，10分位差，10分位比，10分位差比）=（4.5, 0.3, 2, 1)；

异常数据检测：若= 2.9449_4= 3.6512，则判定该样本不含有粗差，其中为标准化样本最大值；_4为粗差界限；

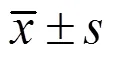
估计结果：原数据范围为[4.1, 5.3]，重复3次估计统示分布参数与总体分布范围的结果如下：

①分布参数：(1,2,3,4) = (4.51, 1.06141, 0.166337, 0.166337 )；

分布范围：[a, b] = [3.56786, 5.45214]；

②分布参数：(1,2,3,4) = (4.51, 0.737381, 0.110353, 0.110353 )

分布范围：[a, b] = [3.15385, 5.86615]；

③分布参数：(1,2,3,4) = (4.51, 1.18289, 0.18882, 0.18882)；

分布范围：[a, b] = [3.66461, 5.35539]。

该估计结果与示例2同样否定按正态性处理识别5.3为异常。

综上所述，在小样本下适于应用分布统示法，且宜按样本分位数估计（采取自助法及多点平均法）统示分布参数后求解待求现实问题，如总体分布范围[,]。显然，按样本分位数估计与按样本矩估计构成两类相辅相成基本方法。

5 高斯混合模型用于粒子滤波

现实的科技问题多具有三非性（非线性、非高斯、非平稳），导致当前不断研究适于求解三非性问题的数据处理方法，如粒子滤波（PF）方法。在现实问题随机性分布信息不足且分布较复杂时，可用适于对称性、非对称性、拖尾型、多峰型等覆盖面最大的高斯混合模型（GMM），以及其样本数据直接统示分布的马尔科夫链-蒙特卡罗（MC-MC）方法。

PF方法实质是以递归贝叶斯统计分析为理论基础的动态滤波方法。过程或系统模型化：

状态空间模型为

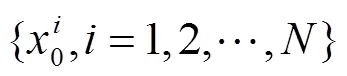
滤波过程的核心问题在于表述滤波过程的后验分布，其核心技术为序贯重要性分布重采样（SIR）。对后验分布作恒等变换

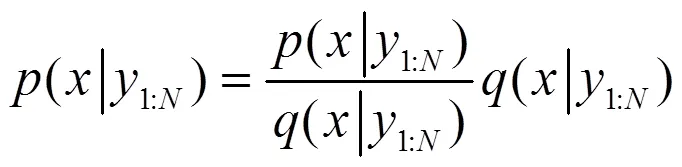
式中，重要性分布(*)可按需任选；(*)为权函数，即归一化加权值。

于是，一列不同的加权粒子样本可逼近不一样的后验分布。为避免粒子退化和样本枯竭而保持粒子集有效性和多样性，按该权值方差确定是否重采样阈值。最后做出任一后验分布期望估计。

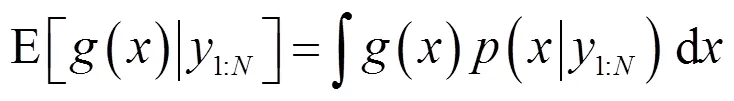
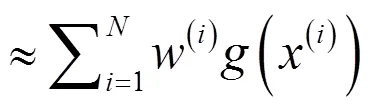
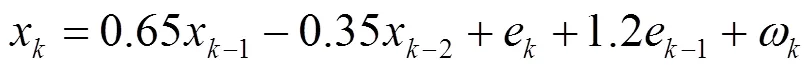
在文献[8]中运用如下方法：尽管其中后一ARMA模型阶数已定的参数估计部分欠妥，应当运用一般参数估计方法。在此仅作为PF算法示例（其中GMM-EM算法见文献[2]）。

---------------------------------------------------------------------

双重PF联合估计状态与参数方法：

For= 1:;

%估计状态

%估计参数

---------------------------------------------------------------------

仿真结果见文献[8]，表明其运行的均方差都较小。初步验证应用GMM-EM及MC-MC方法重采样的PF方法是可行、有效的。

6 结语

本文阐述了当前对小样本数据处理应有的观念、对策与基本方法，及对分布统示法推荐分布、分布及高斯混合分布等应用中应有的观念、对策与基本方法、步骤及应予关注的问题。对分布统示法推荐只是提示性应用，远未能达到解决实际问题程度。其中涉及自助法、异常数据检测、系统误差检测和排除、粒子滤波算法等具体问题和应用，均非一纸即可道明。

[1] 林洪桦.测量误差分析及数据处理若干要点系列论文（一）——现代数据处理基本观念与四字要诀[J].自动化与信息工程,2020,41(1):1-4,9.

[2] 林洪桦.测量误差分析及数据处理若干要点系列论文（二）——随机性分布统示法综论[J].自动化与信息工程,2020, 41(2):1-7.

[3] 林洪桦.测量误差与不确定度评估[M].北京:机械工业出版社,2010.

[4] 林洪桦,潘峰.重复测量数据分布的自助法估计[J].北京理工大学学报,2004(11):947-951.

[5] 林洪桦.再荐误差的分布统示法[J].中国计量学院学报，2004(2):96-101.

[6] 席同鑫,林洪桦,王中宇.误差分布对称性的识别方法研究[C]//第20届测控、计量、仪器仪表学术年会论文集.2010.

[7] 林洪桦,席同鑫,王中宇.分布统示法用于小样本数据处理的探讨[C],第十一次全国误差理论与不确定度学术与教学交流研讨会,海南三亚,2011.

[8] Li Shuhui, Feng Xiaoxue, Lin Honghua, et al. Joint State and Parameter Estimation of Stationary ARMA Model with Unknown Noise[Z]. CCC,Dalian, 2017.

[9] 林洪桦.探讨小样本下“三非”问题的分析与处理[C].第十四次全国误差理论与不确定度学术与教学交流研讨会,南京,2018.

Some Key Points of Measurement Error Analysis and Data Processing Series Papers (3)——Recommended Applications of Random Distribution Uniform Expression Method

Lin Honghua

(Beijing Institute of Technology, Beijing 10081, China)

This paper expounds the applications of random distribution uniform expression method in modern data processing, the difficulties and countermeasures of small sample data processing are analyzed. The moment estimation method ofdistribution uniform expression method, the quantile estimation method ofdistribution uniform expression method and Gaussian mixture models for particle filtering are described in detail, including concepts, countermeasures, basic methods, steps and issues that should be paid attention to.

data processing; mathematical model; error; uniform expression method

林洪桦，男，1932年生，教授，主要研究方向：测试误差分析及数据处理。

TP274

A

1674-2605(2020)03-0001-07

10.3969/j.issn.1674-2605.2020.03.001