渠道段糙率测试计算与分析

邸国平

(山西省水利水电科学研究院，山西 太原 030002)

糙率是反映渠道表面粗糙程度的重要水力要素，在水力学领域里也是最常见的基础参数之一。糙率匹配程度的好坏不仅反映出施工水平的高低，更可能对渠道的过流能力产生一定的影响，同时糙率又不能直接测得，只能借助测试其他水利要素计算所得。目前渠道糙率计算的方法有曼宁公式反求糙率法、能量方程法、二步计算法、流速垂线分布法等方法，本文依托三泉水库渠道段用前两种方法对糙率进行了计算，验证了两种计算方法对实际工程的适用性及其渠道的实际糙率。

1 概况

三泉水库位于山西省新绛县三泉镇，水库建成于20世纪60年代，大坝填筑为均质土坝，坝高13m，总库容690万m3，是一座小(1)型水库，禹门口提水东扩工程修建后，三泉水库成为该工程的一座调蓄水库。

禹门口提水工程主管线起点从位于新绛县的光马渡槽末端，终点到西梁水库，期间设置有许多供水支线。在新绛供水支线中由于三泉支口至三泉水库渠道段是新建渠道，长度为4.09km，光马渡槽至三泉支口(向三泉水库分水口)段渠道过水断面采用梯形断面，输水流量由原设计3.6m3/s加大到6.5m3/s，输水渠道三泉支口至三泉水库段根据需要沿线布置3座机耕桥，5座跌水，2座分水控制闸室[1]。由于没有安装流量监测设备，本次在渠道进出口附近设计安装2个薄壁梯形量水堰，来测量进入渠道及进入三泉水库的流量及水量，通过量测典型断面的水力要素来计算测试断面的糙率，验证其过流能力。

2 测试量水堰设计

根据SL 537—2011《水工建筑物与堰槽测流规范》相关条款规定，结合工程现场实际情况，为了确保本次渠道内设置的量水堰在过流时堰上水头出流为自由出流，本次设计的两个梯形薄壁量水堰布置在1#跌水(桩号SQ0+172.00)及5#跌水(桩号SQ3+158.66)处，上游顺直段及堰上水头量测位置均满足规范相关要求。

2.1 渠道设计过流能力计算

渠道过水断面为梯形断面形式，边坡坡度为0.8，渠底宽为1.1m，深为2.0m，采用混凝土预制板砌筑护面，根据规范要求，结合已建禹门口灌区工程经验，糙率暂取0.016，过流能力采用明渠均匀流公式计算[2]，设计过水流量为6.5m3/s，安装量水堰位置处渠道过流能力计算结果见表1。

式中，Q—流量；A—过水面积；R—水力半径；i—渠道纵向比降。

2.2 薄壁量水堰设计

根据SL 537—2011规范所规定的标准堰的尺寸要求及现场实际情况，1#跌水及5#跌水处梯形堰的设计参数见表2及如图1—2所示，堰板用12mm厚的钢板制作。

表1 渠道过流能力计算表

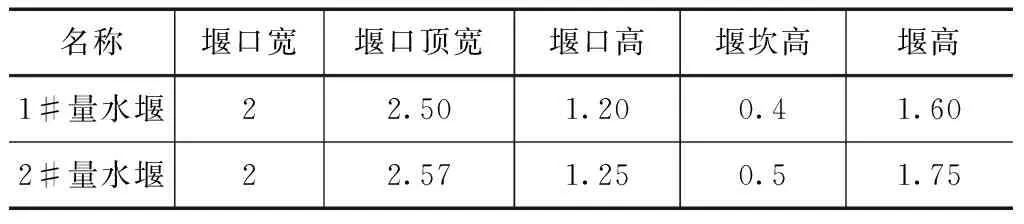
表2 梯形堰设计参数表 单位：m

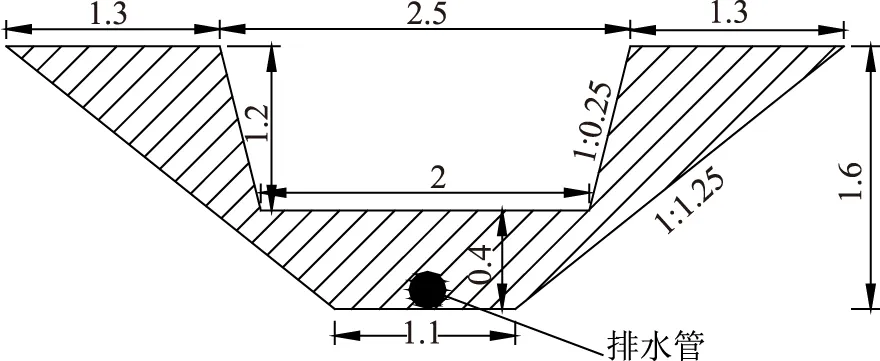
图1 1#量水堰设计尺寸图

图2 2#量水堰设计尺寸图

2.3 薄壁量水堰过流能力计算

根据堰槽测流规范规定，标准堰其断面边坡特定为1∶0.25，结合现场渠道实际情况，实际设计的量水堰部分尺寸超出规范标准堰尺寸，所以其流量系数暂采用1.86的常值[2]，1#及2#梯形量水堰流量计算成果见表3，由于流量的大小只与堰口宽度和堰上水头有关，1#和2#量水堰的堰口宽度相等，所以其流量计算成果两者一致，堰上水头与流量关系曲线如图3所示，流量计算采用如下公式：

Q=CDbh3/2

式中，Q—流量；b—堰口宽度；h—堰上水头；CD—流量系数。

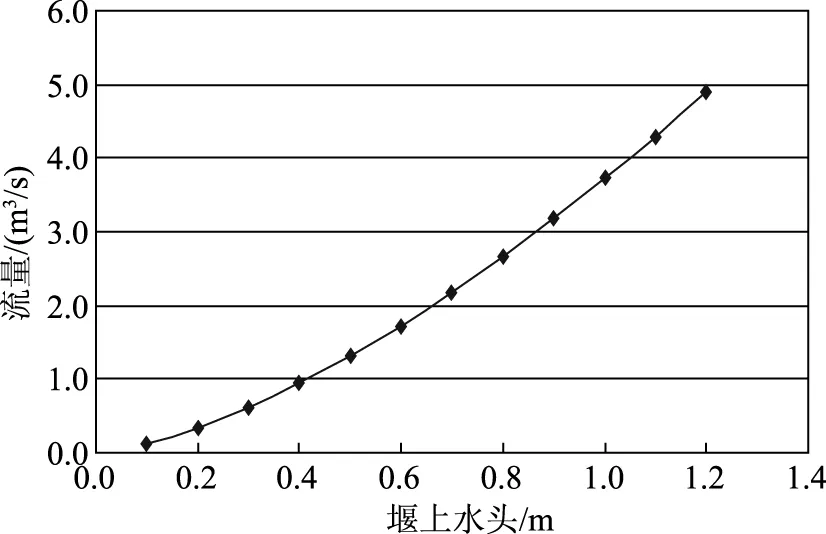
图3 1#、2#梯形堰堰上水头与流量关系曲线

3 渠道糙率计算

渠道表面的粗糙程度是通过糙率来反映的，进行水力计算时糙率也是最重要的参数之一，糙率也是反映施工质量水平的一项重要指标，同时也是影响渠道设计过流能力的重要因素[3- 4]；渠道两侧岸壁及底板的粗糙程度直接影响水流的能量损失，造

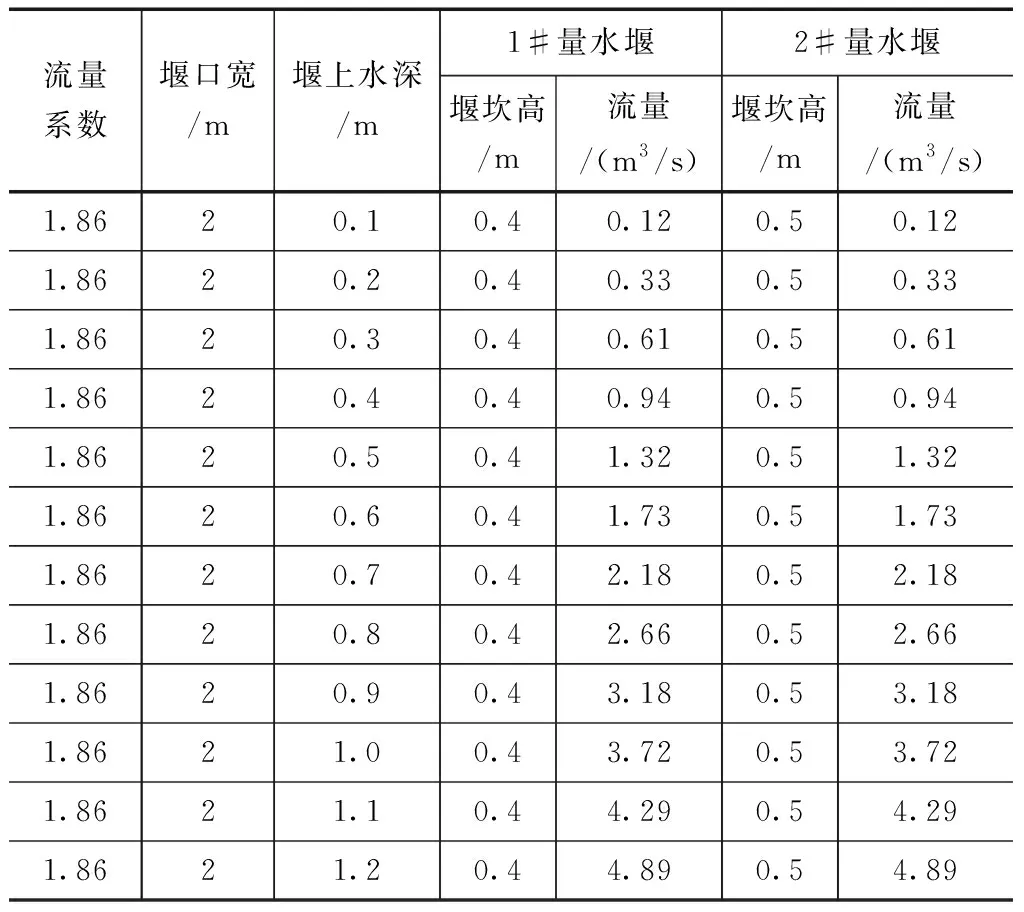
表3 1#及2#梯形量水堰流量计算表

成输水能力降低，水流在渠道中的运动形式多属于紊流运动[5- 7]，其能量损失分为沿程水头损失和局部水头损失，沿程水头损失的大小由渠道边界的粗糙程度决定，边界越粗糙沿程水头损失就越大。

目前研究渠道糙率的一些主要方法有能量方程法，曼宁公式法，二步计算法和流速垂线分布法等[8- 11]，根据现场渠道布置的实际情况、通水时的实测数据以及所应用公式的适用条件，选定桩号为1+653.76—2+429.00、2+790.00—3+123.00作为糙率测试段，下面分别用曼宁公式法和能量方程法进行糙率计算：

3.1 曼宁公式反求糙率(典型断面法)

当渠道内水流流态为恒定均匀流时，根据均匀流的特性，其水体深度、流速沿程不变，可根据实测资料运用曼宁公式反求糙率[9- 10]，曼宁公式为：

(1)

谢才公式为：

(2)

将式(1)代入式(2)得到：

(3)

由式(3)可得：

(4)

式中，n—糙率；Q—断面平均流量；i—比降；R—水力半径；A—过水断面面积。

用曼宁公式法所求4个断面。

3.2 能量方程法(渠段计算法)

用能量方程法来计算糙率[9- 10]，能量方程公式如下：

(5)

式中，Z1、Z2—上、下断面水位；v1、v2—上、下断面平均流速；g—重力加速度；hf、hj—沿程水头损失、局部水头损失；α1、α2—上、下断面动能校正系数。

在较均直的河段，取α2=α1=1，则式(5)移项得：

(6)

对于因过水断面沿程变化引起的局部损失，可由下式来计算：

(7)

式中，ξ—河段平均局部阻力系数。

沿程摩阻损失，可用下式计算：

(8)

式中，Q—流量；L—断面之间的距离；n—平均糙率。

(9)

式中，A1、R1、A2、R2—上、下断面过水面积、水力半径。

将hf、hj计算式代入式(8)整理得：

(10)

或

(11)

式中，Δz—为上游水位—下游水位；ζ—为局部阻力系数；χ1、χ2—为上、下游断面湿周。

所选两断面计算参数及成果见表5。

根据以上表中参数，断面1+653与断面2+429之间糙率计算所得n=0.01694；断面2+790与断面3+123之间糙率计算所得n=0.01484。

3.3 糙率比对

用曼宁公式法选取4个典型断面计算所得糙率分别为0.01687、0.01613、0.01597、0.01547，其平均糙率为0.01611。

用能量方程法选取两个渠道段计算所得糙率分别为0.01694、0.01484，其平均糙率为0.01589。

表4 曼宁公式法糙率计算成果表

表5 能量方程法糙率计算成果表

4 结论及分析

(1)通过实测资料计算结果分析可知，渠道过流能力满足设计要求。

(2)用曼宁公式法选取4个典型断面计算所得糙率分别为0.01687、0.01613、0.01597、0.01547，其平均糙率为0.01611；能量方程法选取2个渠道段计算所得糙率分别为0.01694、0.01484，其平均糙率为0.01589；两种方法计算所得渠道糙率基本一致，保留两位有效数字均为0.016，表明测试段计算所得糙率与原设计值一致。

(3)1#、2#量水堰为临时建筑物，根据量水堰设计布置，渠道过流流量最大不能超过4.8m3/s，在试通水结束后立即拆除，以免影响渠道正常过流能力。

(4)由于本次设计的两座量水堰的部分尺寸超出了规范规定的范围，流量系数采用的是标准堰推荐的1.86的常值，后续将对流量系数做室内模型试验的标定工作，使数据计算结果更加准确合理。