基于TELEMAC与SISYPHE耦合模型的围堰附近砂床局部冲刷的三维数值模拟

谭成宇

(东台市水利建设有限公司，江苏 盐城 224200)

围堰是指为执行水利工程而修建的临时性的围护水工建筑物。它可以防止水土流入工程区域，从而使得受保护区域在施工期内的工程建设得以正常运行[1]。但是，围堰的修建一般会缩小河道的断面尺寸，提高局部流速，从而增大河床剪切应力。当河床的剪切应力超过河床的临界切应力时，就会引发河床的局部冲刷，可能造成施工围堰乃至整个工程的破坏[2]。因此，分析与预测施工围堰造成的局部冲刷可以为围堰的优化设计与安全评价提供必要的信息[3]，具有非常重要的现实意义。河床冲刷的预测分析一般可以采用经验法、试验法和数值模拟法。经验法操作简单，但是精确度往往难以满足要求。试验法较为精确，是当前最可靠的方法，但是，大尺度的试验的时间与物力成本过高，而小尺度的物理模拟则可能会因为比例缩放问题而引发预测精确度的下降。随着近年来计算机技术与资源的不断发展，数值模拟法在水利工程领域得到了越来越广泛的应用[4- 6]。TELEMAC是由法国电力集团开发的一款计算流体力学平台[7]。它的一项重要优势是免费且开源，因此，采用它建立模型可以降低成本、掌握源代码以及为以后增减模型功能提供基础。但是，标准的TELEMAC无法进行泥沙冲刷淤积的模拟。因此，本文提出将SISYPHE泥沙冲刷淤积模块与TELEMAC进行耦合，并采用该耦合模块完成围堰周围河床冲刷淤积三维数值模拟的方法。据笔者所知，基于TELEMAC与SISYPHE的围堰局部冲刷三维数值模拟尚未被报道过，而其是否有能力准确模拟围堰的局部冲刷亟需验证。

因此，本文的主要目的是建立基于TELEMAC与SISYPHE耦合模型的围堰附近泥沙冲刷模型并对其进性能进行评价。首先，进行围堰局部冲刷的物理试验，得到围堰附近的冲刷实测数据，该数据不仅可用于本文数值模拟的验证中，也可以为其它模型的验证提供资料。其次，应用TELEMAC与SISYPHE耦合模型建立数值模型并根据试验工况条件进行模拟。最后，将模拟结果与试验值进行比较并对其精确度进行分析。结果表明，基于TELEMAC与SISYPHE耦合模型的围堰附近泥沙冲刷模拟结果接近实测值，满足工程要求，因此具有较好的推广价值。

1 方法

1.1 试验方法

不同的数值模型所得结果往往相差较大，因此，必须要对其进行验证。本文首先进行物理试验，以便于为数值模型的验证与评价提供实测数据。试验的基本设置如图1所示。试验水槽长度2.5m、宽度0.35m。围堰沿x轴方向的长度为5cm、沿y轴方向的长度为15cm。水槽利用水泵进行水流循环，上游(图1左侧)为水流入口，流量为0.005m3/s，下游(图1右侧)为水流自由出口。水槽铺有石英砂，其D50粒径为0.001m。试验主要关注超临界流的冲刷过程，因此，当水流达到出口后则停止水循环，之后采用高度测量仪测量砂床的冲刷情况。根据初步试验结果可知，本试验中的主要泥沙冲刷淤积位于距离围堰的y轴正方向边缘(以下简称为“前边缘”)约5cm的范围以内，其它区域的砂床高程变化几乎忽略不计，因此选取该范围为研究区域。因此，研究区域的x坐标介于-5～10cm之间，y坐标介于-7.5～5cm之间。测量点分布间距为1cm，因此在研究范围内共设置72个测量点，其分布如图1中圈状标记所示。

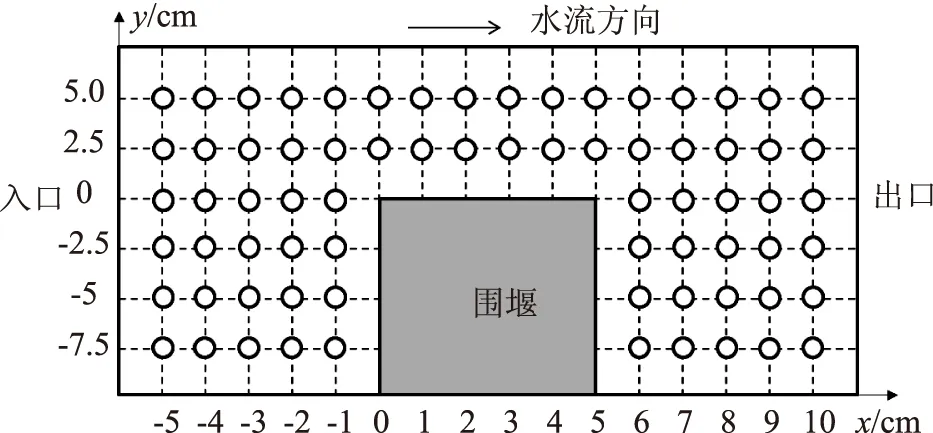
图1 试验设置与测量点分布图

1.2 模拟方法

数值模拟在开源平台TELEMAC中进行。将之与SISYPHE模块进行耦合，从而可以进行泥沙冲刷淤积的计算。

水动力模拟可采用标准的Navier-Stokes方程，其表达式为：

(1)

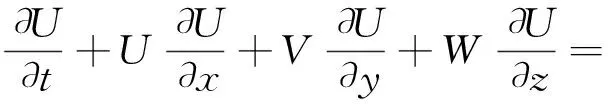
(2)

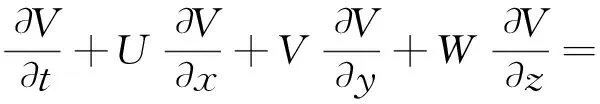
(3)

(4)

式中，x、y、z—顺水流方向、横向和纵向的坐标；U、V、W—在x，y和z这3个方向上的速度分量；p—压强；patm—大气压强；ν—黏性系数；ρ0—参考密度；Δρ—密度的变化值；Fx、Fy—其它的外力。

河床的高程变化、即泥沙的冲刷与淤积采用泥沙守恒公式[8- 9]，其表达式为：

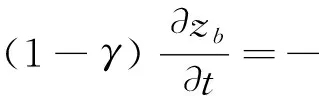
(5)

式中，γ—砂床的孔隙率；zb—砂床的高程；t—时间；qB—近底泥沙通量；D—沉降率；E—与夹带率。其中泥沙通量的计算采用经典的Van Rijn方程[10]计算。

水动力与泥沙冲刷淤积的耦合过程如图2所示。首先，读取初始的河床高程信息，并采用TELEMAC的标准水动力求解器计算流速、压强等水力参数。之后，将求得的水力参数提供给SISYPHE的泥沙冲刷淤积模块，该模块首先也是读取原始的河床信息，之后，求解泥沙守恒方程求得河床高程的变化。最后，新的河床高程信息被传送回水动力模块作为新的原始河床高程，并进行下一时间点的水动力模拟。

图2 数值模型流程示意图

2 结果与讨论

2.1 试验结果

本次试验的结果呈现于图3中，其中横轴为x坐标，纵轴为砂床高程的变化值。比较图3中各图的河床高程变化量级，沿y轴负方向观察，当断面距离围堰较远时(如y=5cm)，河床冲刷深度约为0.5cm，当较为接近时(如y=2.5cm和y=0时)，河床冲刷深度接近1.5cm，冲刷深度逐渐增加。当断面继续沿y轴负方向渐远时(如y=-2.5cm)，最大冲刷深度逐渐变小至1cm左右，当断面远离围堰前边缘时(如y=-2.5cm和y=-7.5cm时)，河床冲刷深度继续变小，最终接近于0。冲刷深度在x轴方向的冲刷深度分布可以通过观察各图中河床高程变化值随x值的变化情况进行分析，但y=-2.5cm和y=-7.5cm这两个断面的冲刷深度较小，且沿x轴的分布比较均匀，因此不作比较。对于其它各断面，泥沙的冲刷深度大体上呈现由x=-5cm至x=0逐渐增大的趋势。在x=5cm断面的冲刷深度一般大于x=0断面处的

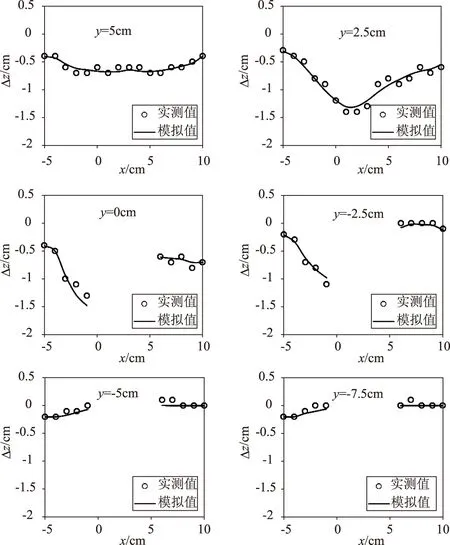
图3 实测与模拟河床高程变化值

深度。综合上述分析，在y方向上，泥沙冲刷在围堰前边缘较为严重；在x方向上，泥沙冲刷在围堰的上游边缘较为严重。因此，图1中横坐标为x=0、纵坐标为y=0的位置可能出现最大的冲刷深度、稳定风险最高，之后冲刷深度沿各个方向随距离的增大而逐渐变小。

2.2 模拟结果

图3中实线代表模拟结果。对模拟曲线进行观察可知，在x小于0的范围内(即围堰上游)，泥沙冲刷深度沿着横轴正方向而逐渐增大，在x大于5cm的范围内(即围堰下游)，泥沙冲刷深度沿着横轴正方向而逐渐减小。在y大于0的范围内(即围堰前边缘侧)，泥沙冲刷深度沿着y轴负方向而逐渐增大，在y小于0的范围内(即围堰后边缘侧)，泥沙冲刷深度沿着y轴负方向而逐渐减小。以上结论与实验结果基本一致，因此可以认为该数字模型可以非常准确地模拟出泥沙冲刷深度的分布规律。

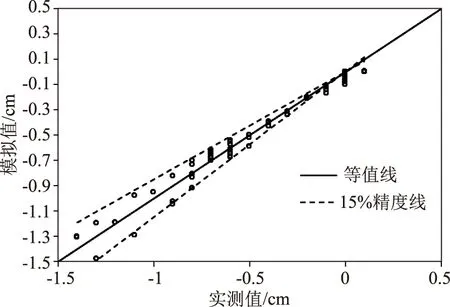
图4 实测值与模拟值的散点比较图

为进一步分析定量地判断数值模型的模拟性能，做散点图于图4中，其中横坐标代表试验值，而纵坐标代表数值模型所提供的结果。图中实线为等值线，当各散点距离其较远时，则认为模拟结果偏差较大，反之则较小。当各散点坐落于等值线的上部时，则认为模拟值偏向于高估了淤积值(即低估冲刷值)，反之则有低估了淤积值(即高估冲刷值)的趋势。根据图4发现，各散点非常接近于等值线，且较为均匀地分布于等值线的两侧，因此可以认为其可以非常准确地预测围堰的局部冲刷。图4种的虚线为15%精度线，大部分散点位于两条15%的范围以内，即大部分模拟值的精确度均保持在15%以内。个别散点超过15%的范围，但这几个散点较接近于0，即泥沙冲刷深度较小，因此，误差的绝对值也较小，而且，超出15%精度线的点主要分布于等值线下方，即高估了泥沙冲刷深度，偏向保守。因此，模拟结果证明该模型在施工围堰的局部冲刷模拟中效果良好，满足一般的工程要求。

2.3 误差分析

为进一步了解该模型的模拟性能，对数值模拟的结果进行量化的误差分析，所选用的指标包括平均绝对百分比误差(MAPE)、平均相对误差(MRE)、平均绝对误差(MAE)、均方根误差(RMSE)、决定系数(R2)，平均偏差(MBE)和标准化的均方根误差(NRMSE)。各误差指标的计算公式分别为：

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式中，xcalc—模拟值，；xobs—实测值。

结果汇总于表1中，在y=-2.5cm，y=-5cm，和y=-7.5cm断面均有冲刷深度值为0的数据，因此这几个界面的MAPE、MRE和NRMSE值无意义、不列于表1中。根据表1中的MBE和MRE值可知，各断面模拟值的平均偏差和平均相对误差非常接近于0，因此整体上不偏向于高估或者低估。在绝对误差方面，MAE和RMSE值的平均值为0.05cm和0.06cm，均较小，取其中较大值，可以认为该模拟的绝对误差为0.06cm。在相对误差方面，MAPE的平均值为7.34%，而NRMSE的平均值为0.1，即10%，均满足误差小于15%的一般工程要求，取其中较大值，可以认为该模拟的相对误差在10%以内。

3 结语

通过进行围堰附近局部河床冲刷的物理试验，得到围堰周边冲刷点的高程变化数据，该数据不仅可用于本文数值模拟的验证中，也可以为其它模型的验证提供资料。基于TELEMAC与SISYPHE的耦合模型对该试验进行了三维数值模拟，并且与试验结果进行对比。模拟结果与实测的砂床变化高程数据具有较好的吻合度，模拟所得的冲刷深度分布规律与试验基本一致，平均误差值约为0.06cm、相对误差约为10%。因此，证明了该方法在施工围堰局部冲刷计算中的有效性，为提高当前的围堰附近河床冲刷淤积的预测水平提供了有效的参考。本方法可以用于进行数值模拟试验以分析不同的影响因素对砂床冲刷的影响，从而有助于设计合理的围堰设计方案并进行有效的工程安全评，因此具有重要的现实意义。TELEMAC和SISYPHE均开源代码，因此，在未来可以继续对其进行改进，以进一步提高其模拟精确度。

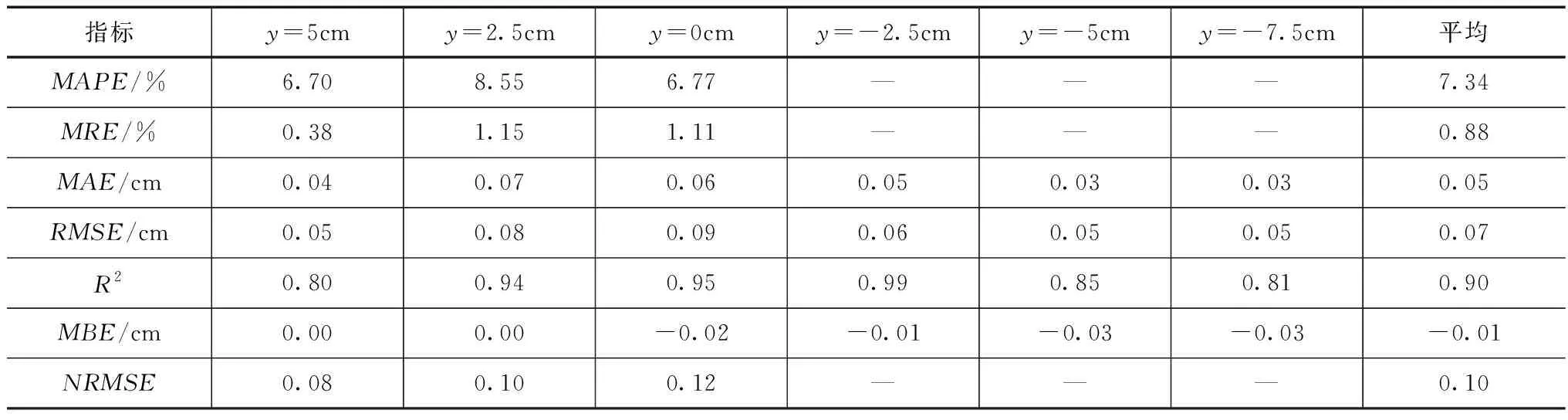
表1 数值模拟误差分析