具有速度、加速度约束的机器人编队避障控制
张志伟,滕英元,杨慧欣,倪智宇
(沈阳航空航天大学航空宇航学院,辽宁沈阳 110136)
1 引言
机器人技术是一项融合跨学科的高科技领域技术,机器人编队控制广泛应用于巡逻、搜救、侦察、空间探测等领域[1-6].机器人编队避障控制问题是一项基础且关键的重要问题,受到人们广泛的关注,已经成为科技研究的热点[7-9].最新文献表明,机器人可以作为一个工作组合作完成监视任务或者在敌对地区从事间谍工作[10-12].在民用应用中,需要系统来自动驾驶车辆.此外,在物联网中,需要机器人来合作运送物品.
目前比较流行的循环追踪(cyclic pursuit)控制思想实际上是从生物学的角度得来的,如蚁群算法[13]、飞行中的鸟群[14]等,可以分为线性循环追踪(linear cyclic pursuit,LCyP)和非线性循环追踪(nonlinear cyclic pursuit,NlCyP).研究表明[15-17],当人们用线性循环追踪的思想描述多个体系统达到平衡状态时,个体的运动轨迹在平衡点处稳定,而多个体的线性循环追踪将收敛到编队的初始中心[18-19].人们对于非线性模型下的循环追踪控制问题和稳定性进行了分析,研究表明[20-23],非线性的循环追踪编队形成稳定构形时,其编队中心也被初始位置固定.当LCyP与NlCyP应用于即时、在线控制时,可以收敛到期望的构形,且具有较好的稳定性与鲁棒性.稳定运行的编队,其中心位置与运动过程无关,始终保持在初始几何的中心,而且在编队达到稳定前,无法提前确定稳定构形的中心位置.从实际应用角度看,这就降低了其适用性,使得一些具有特征典型的任务设计无法实施.要改进编队中心可变的性质,就需要引入新的控制算法,如引入非成员的导引参考,用于保证固定信标周围机器人运动的全局渐近稳定性.Ceccarelli等在研究多个体系统(multi-agent system,MAS)的集体定位行为时,提出了引入虚拟参考航标作为运动导引的思想[24],对单个具有指定旋转方向的成员,设计了具有全局渐近稳定性的“航标”导引控制法则,较好地解决成员与指定点的相对位置问题.
同时,在编队运动过程中,对机器人速度和加速度大小没有限制.而在实际应用中,机器人本身对速度和加速度的大小有一定的限制,当速度和加速度大小超过机器人的截断速度时,机器人只会以自己允许的最大速度运行.Ren、张玉杰等[25-26]利用控制Lyapunov函数方法克服了输入约束对控制器设计带来的困难.Gu、顾万里等[27-28]提出了一种适用于速度受限移动机器人的跟踪控制器.该算法考虑了移动机器人的速度约束,对于移动机器人的执行器,无法跟踪加速度过大的速度命令.Chen X等[29]研究了单机避障问题,结果表明,在速度和加速度约束条件下,单机的避障识别和控制效果很好.Wang Zhiteng等[30]分析单机的避障控制原理,在不考虑最短路径时,避障控制效果显著.对多移动机器人避障问题的研究,以往人们常采用B rooks[31]提出的基于行为的反应式控制及宋梅萍等[32]提出的基于规则的控制策略等方法,这些方法适用于任务和环境很简单的情况.四叉树法[33]更适用于模型环境不发生动态变化的情况.张纯刚等[34]提出的基于局部感知的窗口滚动法,适用于未知环境,并给出了局部最优解.Giuseppe Franzè 和Walter Lucia[35]提出了滚动时域策略,用于解决动态环境中线性定常系统所描述的自主移动机器人的路径规划问题.
本文在前人工作的基础上,聚焦于避障识别的实域性,即避障的识别及算法的时效性,即收敛的效率.设置了不同的局部控制增益,考虑了速度和加速度约束,同时引入了惩罚因子.采用该优化算法,实现了以下3个功能:1)实现非失效机器人的降级重组,避免机器人之间发生碰撞;2)实现控制算法的稳定与收敛;3)解决了机器人编队构型稳定后向前行进过程中的避障问题.研究结果验证了所提控制方法的正确性和有效性.
2 多机器人的编队模型
机器人的位姿用[x y θ]T表示,(x,y)∈R2表示个体在平面内的位置,θ表示运动方向,(u,ω)∈R2表示切向速度和角速度控制输入.因此,机器人的运动方程为
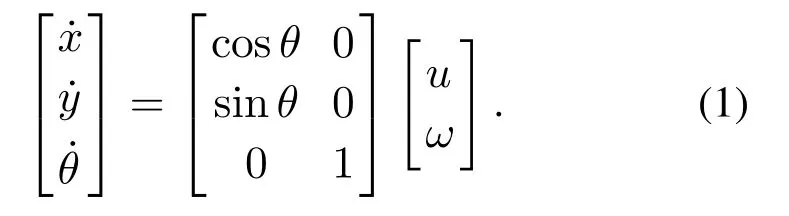
因此,动力学模型为
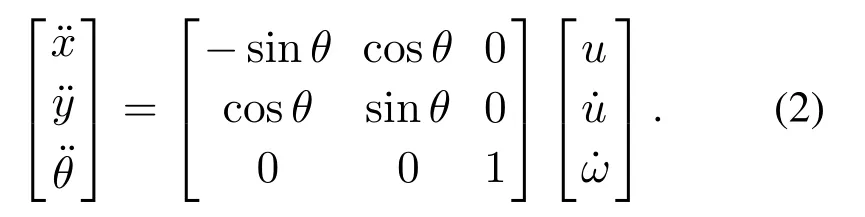
本文采用的多机器人编队方式如图1-2所示.
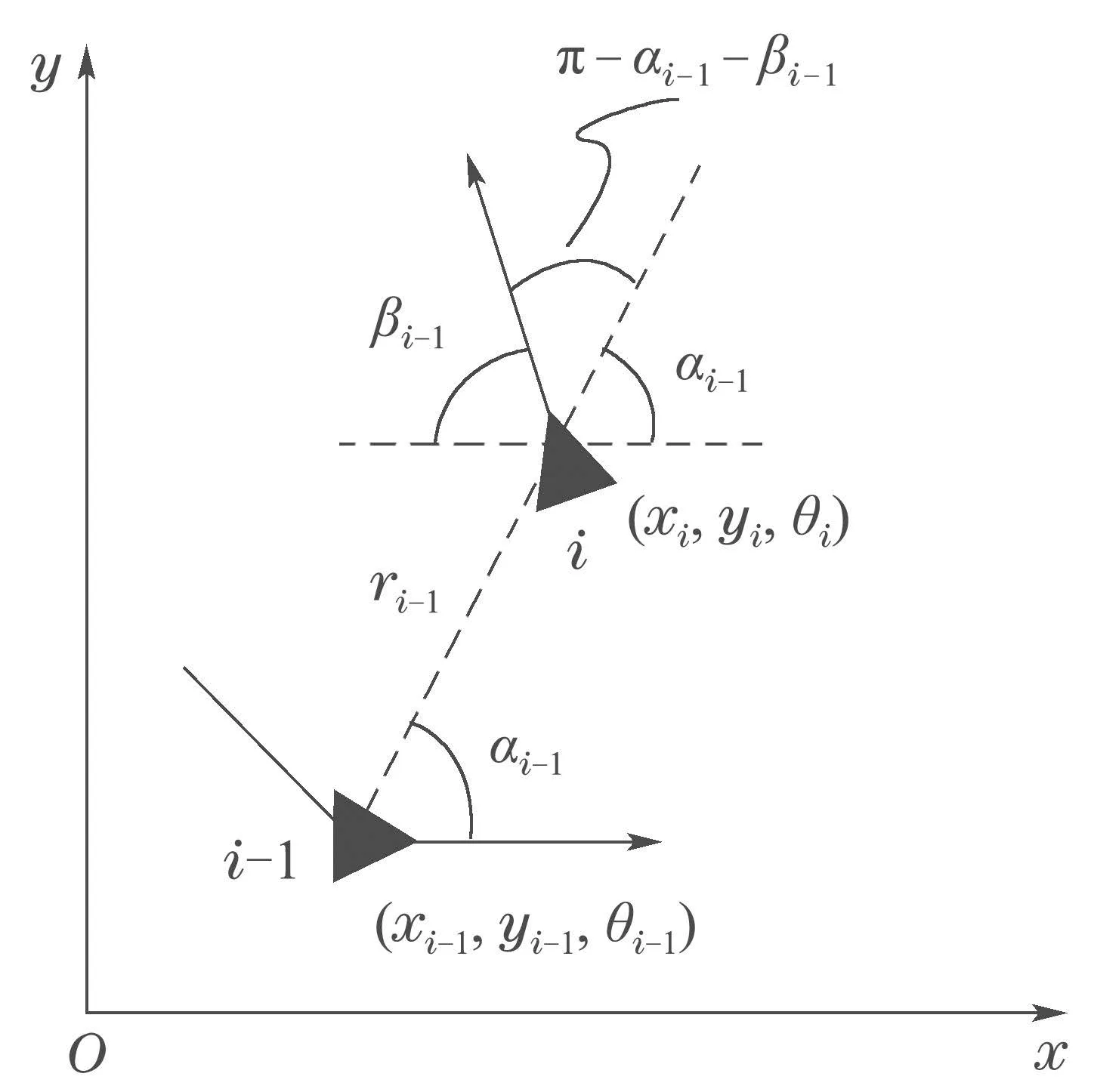
图1 循环追踪系统相对坐标Fig.1 Relative coordinates of cyclic pursuit system

图2 多机器人编队构型Fig.2 Multi-robot formation configuration
图中:(xi,yi,θi)表示前边第i个机器人的位置和导向角,(xi-1,yi-1,θi-1)表示跟随的第i-1个机器人的位置和方向.ri-1表示机器人i与i-1之间的距离,αi-1指从机器人i-1速度方向与机器人i连线方向的夹角,βi-1表示机器人i-1速度方向与机器人i速度方向夹角的补角.
因此,多移动机器人编队的运动方程为
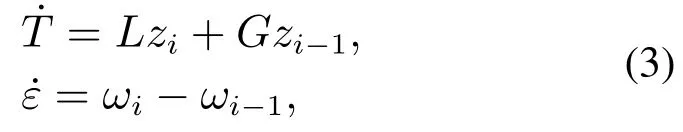
其中:T=[ri-1φ]T; φ=π-αi-1-βi-1; ε=θiθi-1是机器人i和机器人i-1的相对方位;zi和Zi-1分别是机器人i和机器人i-1的速度矢量.
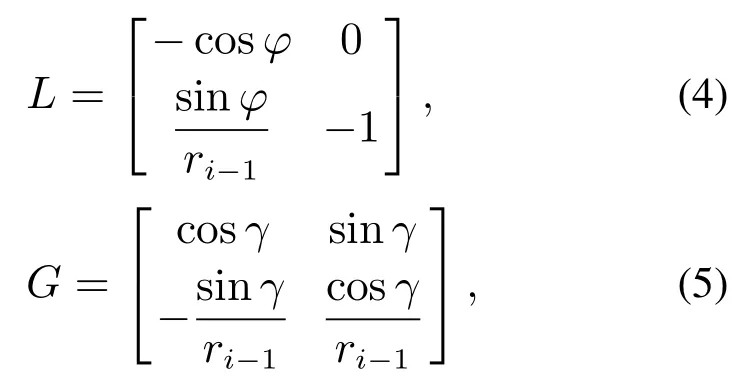
其中γ=φ+ε.值得注意的是T,γ和φ分别是T(t),γ(t)和φ(t)的瞬时值,所以T的值为
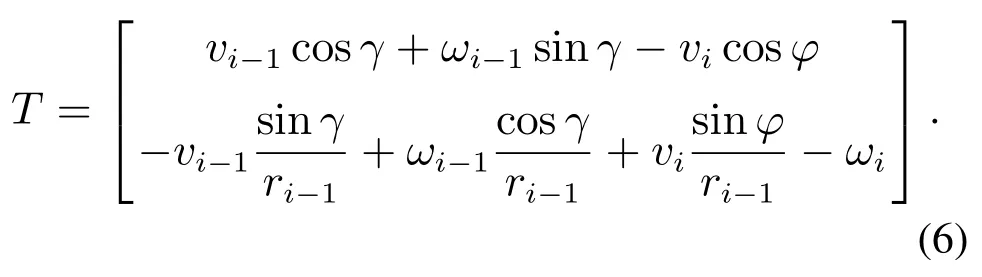
3 控制算法优化
对于NlCyP控制的机器人编队,在其期望的编队中心设置“航标”(navigation’s beacon,NB),引导机器人循环追踪完成均匀分布的同时,通过引入了非成员的参考功能解决其集体定位问题,使其能够收敛到相对“航标”的指定距离.“航标”示意图如图3所示.

图3 机器人相对航标示意图Fig.3 Diagram of robot relative navigation’s beacon
由于定速追踪的运动是变速追踪的稳定情况,所以,设机器人编队达到稳定速率vR前,速率按vi=krri变化,kr为常数.基于NB 控制律[24]对系统实行全员“航标”引导的非线性循环追踪控制编队时(nonlinear cyclic pursuit in navigation’s beacon to all agents,NlCyP&NB-a),运动学方程为

机器人组成的MAS编队,假设编队前机器人的初始坐标定义为[x,y].
3.1 降级重组
当编队过程中个别成员出现监测执行功能失效问题(但仍能运行)时,NlCyP&NB-a控制算法可实现对非失效机器人进行系统降级重组,其目的是实现正常运行的机器人仍保持均匀分布进行工作,同时也要保证控制过程中正常机器人与监测执行功能失效机器人不会发生碰撞.
如果失效机器人成为新的避障问题,本文从识别到避障会形成合理的闭路循环,新的避障会循环至初始,形成新的识别和新的避障.可以实现对失效机器人的处理,从而实现多移动机器人的编队避障.
NlCyP&NB-a控制下的相位调整,其关键是机器人的速率、控制增益kα与期望状态的匹配.若各机器人稳定速率相同,则通过调整局部控制增益kα值来达到目的效果.改变ui,通过分别设定不同的控制增益值kα1,kα2,kα3,kα4来实现降级重组.

3.2 引入速度、加速度约束
考虑到一些轮式移动机器人只提供速度控制接口,而机器人电机不能跟踪加速度过大的速度指令,对于不考虑约束的机器人,当控制量超过约束界限时,应用于物理机器人系统的控制输入会截断,截断控制输入会降低控制器的性能,甚至使被控系统失稳.因此引入了速度和加速度约束.
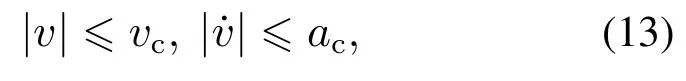
其中vc和ac是常数.机器人速度和加速度约束大小约为vc=0.6 m/s,ac=1.12 m/s2.当速度超过速度束时,系统会做出截断,截断的响应时间为t=100 s,因此在此期间内系统会增大控制增益kα和kb使之迅速达到要求.
当vi>vc时,则
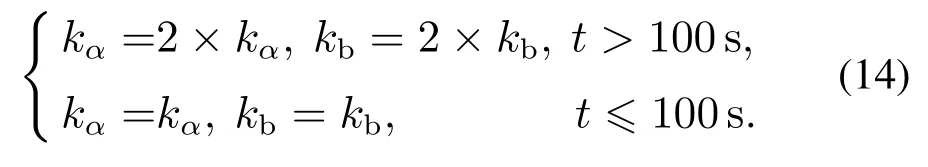
3.3 路径规划、避障控制
为了避免机器人在编队形成稳定的构型后,向前行进过程中与障碍物发生碰撞的危险,提出了引入惩罚因子的概念以淘汰不安全路径.本文主要研究编队中心到目标点的最短路径规划.惩罚因子是一个施加在路径长度的系数,见式(15):
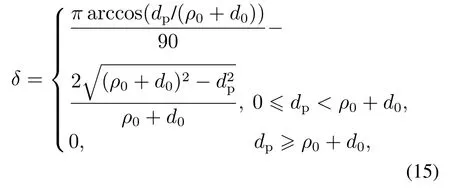
式中:δ代表惩罚因子,d0为单个机器人与障碍物之间的安全距离,dp表示选择的路径和障碍物之间的最短距离.
假设最短路径长度为lk,综合考虑路径中的障碍,得到安全最短路径长度Lk:
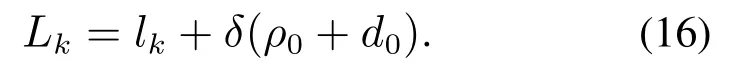
由式(15)-(16)可知,当0≤dp<ρ0+d0时,说明路径和障碍物之间的距离过近,机器人选择的路径为不安全路径,惩罚因子δ变大,得到的安全最短路径长度Lk也相应变大;当dp≥ρ0+d0时,说明路径和障碍物之间为安全距离,机器人选择的路径为安全路径,惩罚因子δ值为0,安全最短路径长度Lk与lk等长.
证定义编队中心初始位置为(x1,y1),运动目标位置为(x2,y2),如图4-5所示,其中M1-M4分别代表不同的机器人.

图4 机器人编队安全边界Fig.4 Safety boundary of robot formation

图5 机器人编队中心运动轨迹Fig.5 Trajectory of robot formation center
x2>x1,障碍物的位置坐标为(a,b),且0≤dp<ρ0+d0,所以最短路径为
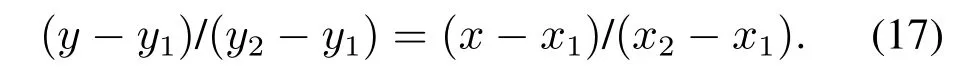
最短路径长度lk为
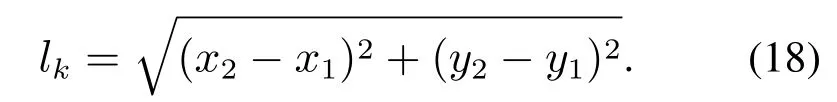
由于编队为圆形,所以考虑每个机器人与障碍物的安全距离时,可直接转化为编队中心与障碍物的安全距离为(ρ0+d0),因此在障碍物周边的最短安全路径为

同时联立式(17)(19)即可求出交点坐标分别为A(m1,n1),B(m2,n2),其中m2>m1.
所以整个机器人编队到达目标点的安全的最短路径为

所以,此时安全的最短安全路径长度Lk为

此时可得惩罚因子为
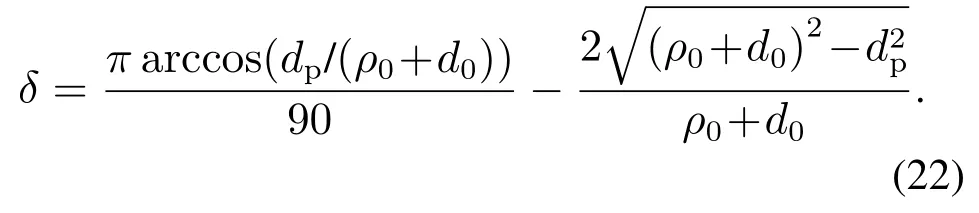
证毕.
4 仿真结果
此时,假设由三机器人组成的MAS编队(M1,M2,M3),初始坐标分别为M1[0.496,-99.999],M2[86.849,-49.57],M3[-86.354,-50.429].当改进ui中的kα都为统一值kα=时,对系统实行NlCyP控制,稳定时编队中心与初始几何中心(原点)不重合,如图6所示.此时若设kb=0.01,cb=2,其余参数保持不变,对系统实行航标在原点的NlCyP&NB-a控制时,编队中心在原点附近稳定,运行结果如图7所示.以下所有图中彩色图形代表了不同机器人的初始位置,黑色图形代表了不同机器人的最终位置.
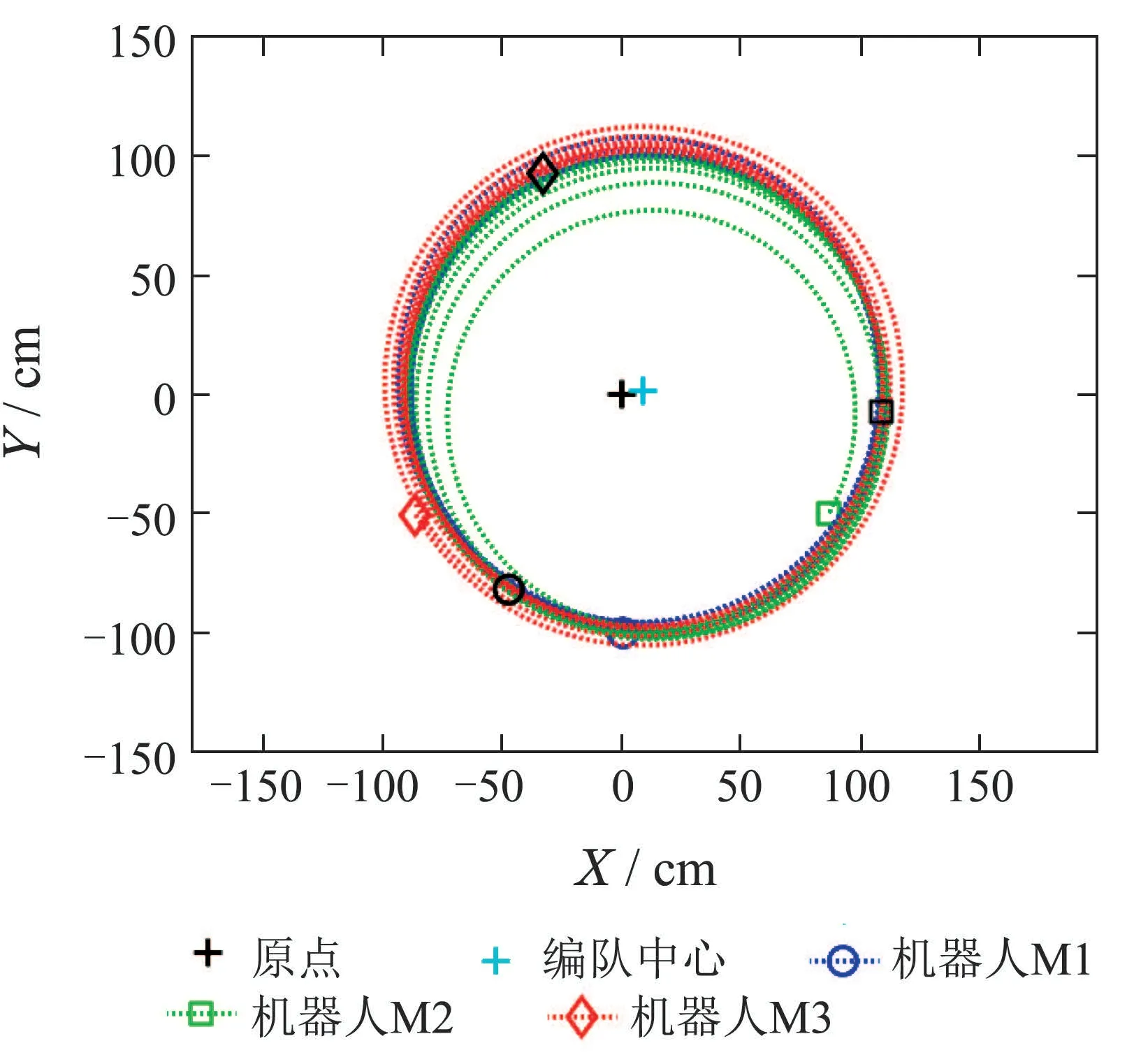
图6 NlCyP控制编队运行轨迹Fig.6 NlCyP control formation trajectory
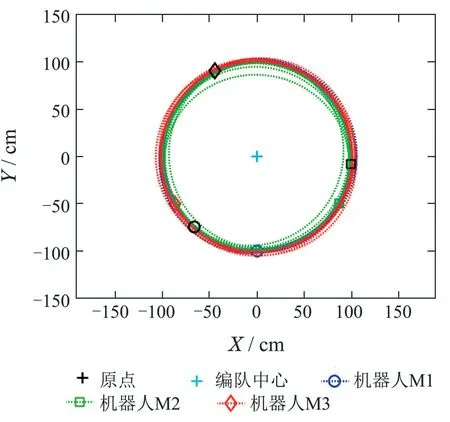
图7 NlCyP&NB-a控制编队运行轨迹Fig.7 NlCyP&NB-a control formation trajectory
相比于以往控制方法,NlCyP&NB-a控制可以实现“航标”为原点进行{n/1}追踪运动,编队中心可变,整个编队在收敛到稳定构形的同时,其编队中心也将向“航标”收敛,当速率均稳定在vR,则该系统将进化为以原点为中心的广义正多边形.
与文献[23]的经典算法进行比较(取稳定值浮动1%时的计算步step作为对比)见表1.

表1 算法对比Table 1 Algorithm comparison
由此可见,本文所采用的算法在效率、稳定性、收敛速度具有较好的效果.
4.1 降级重组
编队成员为4 个机器人(M1,M2,M3,M4),假定M3机器人失效,即期望正常机器人均布,失效机器人M3位于M2与M4中间.其他的初始参数设置见表2,ψ为4个机器人的初始相位角,U为控制输入电压,单个步长step为100 s.

表2 初始参数值Table 2 Value of initial parameters
于是,得到的仿真结果如图8-9所示.图8中彩色图形代表了机器人的初始位置,黑色图形代表了最终位置.可以看出,编队的半径为1 m,失效机器人M3位于M2,M4之间,所有的机器人达到了稳定的状态,正常机器人实现了均匀分布状态,编队中心坐标稳定在原点.仿真达到400步时,机器人相对参考中心距离趋向稳定.

图8 四机器人NlCyP&NB-a控制轨迹Fig.8 NlCyP&NB-a control trajectory of four robots

图9 四机器人相对航标距离Fig.9 Distance of four robots relative to navigation’s beacon
正常机器人相对距离与正常机器人相对监测执行功能失效机器人距离分别如图10-11所示.可以看出,正常机器人之间相对距离约为1.75 m,失效机器人M3与正常机器人M2,M4之间距离约为1 m,与正常机器人M1的距离约为2 m.

图10 正常机器人(M1,M2,M4)相对距离Fig.10 Relative distance of normal robot(M1,M2,M4)
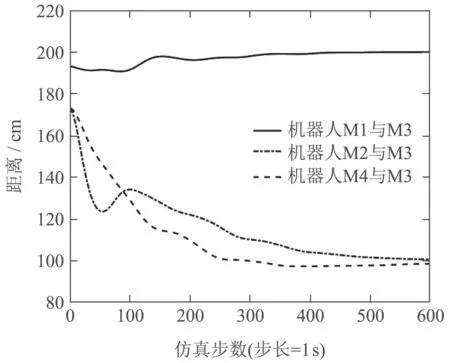
图11 正常机器人(M1,M2,M4)与失效机器人(M3)距离Fig.11 Distance between normal robot(M1,M2,M4)and failure robot(M3)
因此,在个别成员出现监测执行功能失效的情况下,只要参数匹配,编队仍能达到循环追踪的理想构形,为多机器人的编队增强了鲁棒性,防干扰和编队继续执行任务的恢复能力.
4.2 引入速度、加速度约束
从图12-13中可以看出,机器人的速度和加速度最终都趋向稳定,速度约为0.313 m/s,最大约为0.323 m/s,加速度最大约为8.2×10-4m/s2,最终加速度趋向于0.
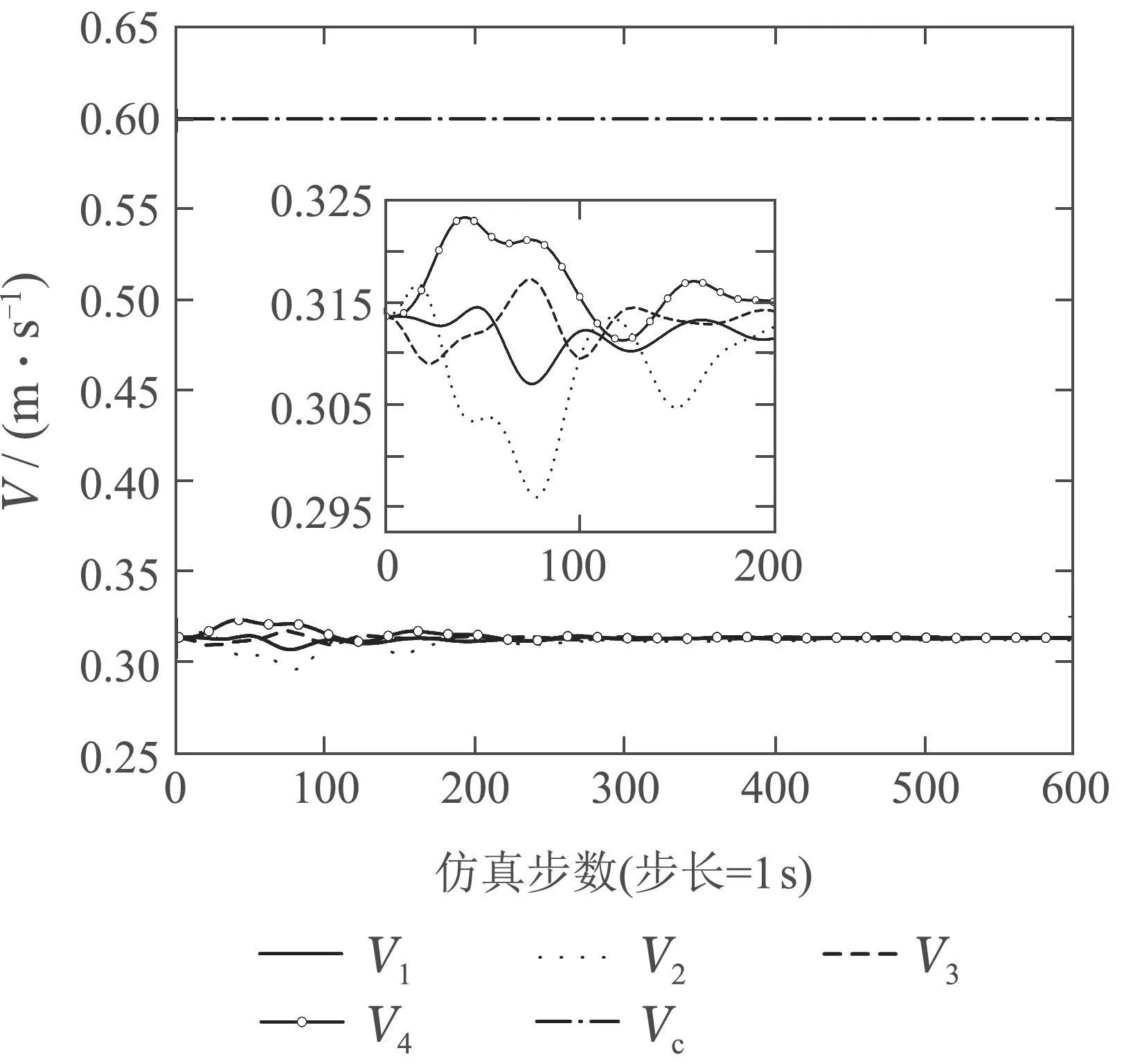
图12 速度图像Fig.12 Velocity diagram

图13 加速度图像Fig.13 Acceleration diagram
当速度超过0.6 m/s的速度约束时(见图14),控制增益变大,此时,

机器人在100 s内迅速降低到约束值以下,而不被截断,继续执行任务,见图15.
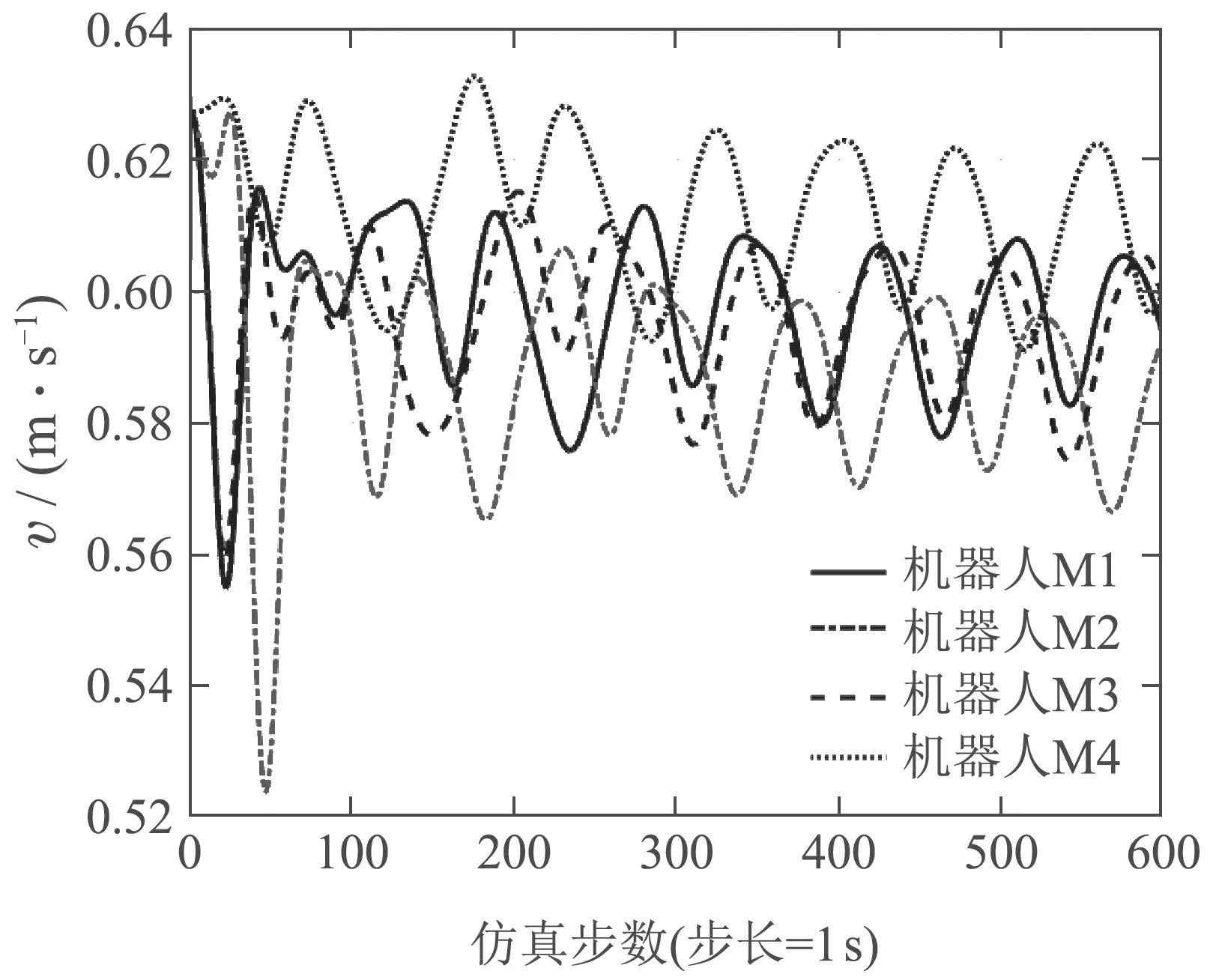
图14 机器人速度超过约束Fig.14 Robot speed exceeds constraint
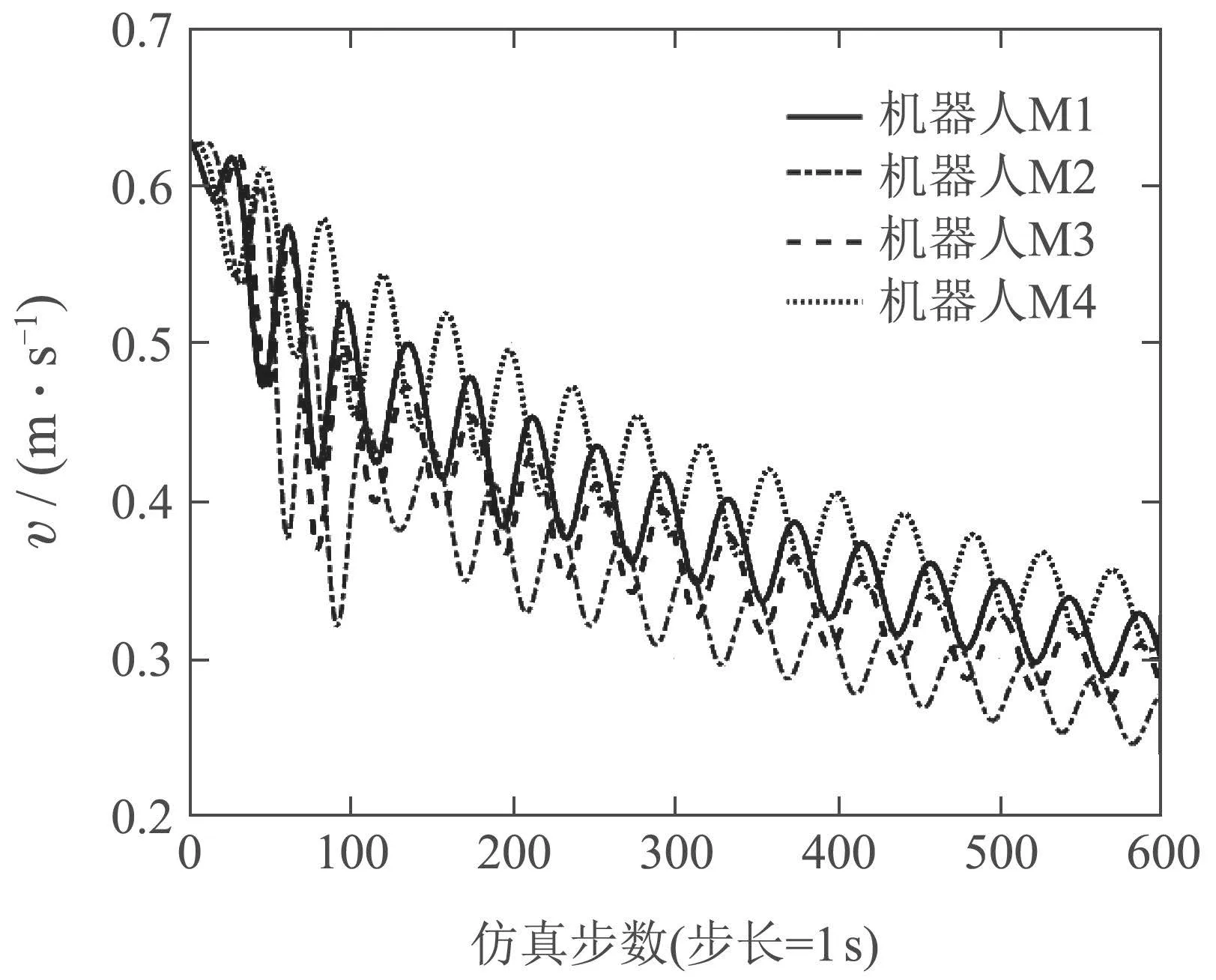
图15 增大kα,kb后速度Fig.15 Speed after increasing kα,kb
由此可见,在一定范围内调整kα,kb以满足速度变化的要求,机器人编队调整应使相位、速率与控制增益kα,kb匹配.控制增益参数kα与kb二者要平衡,以保证匹配的预期.当较多成员分担的NB控制时,kb取值也相应减小.控制增益具体参数的选取,以参考文献[18,24,36]得到大致范围为初始参数,通过多次反复调试,最终得到识别和收敛效率最好的优化参数组合.
4.3 路径规划、避障控制
具体参数设置见表3,其余参数与前边得到的数据相同.

表3 初始参数值Table 3 Value of initial parameters
表3中λ为编队完成后4个机器人的相位角.
图16-18分别表示障碍物位置对降级重组后4个机器人的影响.图16为障碍物远离机器人编队,图17表示障碍物处于起止点连线下方,图18表示障碍物处于起止点连线上方,因此图16的障碍物对机器人编队基本没有影响,图17-18只是有影响,只是因为障碍物位置不同,运动轨迹不一样.

图16 无障碍运动轨迹Fig.16 Obstacle-free trajectories of motion

图17 有障碍运动轨迹Fig.17 Motion trajectories with obstacles

图18 有障碍运动轨迹Fig.18 Motion trajectories with obstacles
此惩罚因子引入的优点是:无论障碍物多少或处于什么位置,编队规划的路径始终为最短路径,这样大大节省了机器人编队运行时间.
5 结论
为了实现多机器人复杂情况的编队避障控制,本文研究了具有速度、加速度约束的改进的控制算法,并且引入惩罚因子的不同控制增益的NlCyP&NB-a控制方案.该方法关键特征是全局稳定性和鲁棒性,提高了抗干扰及规避障碍的能力,实现了只有局部控制信息的多机器人编队.
1) 不同的局部控制增益,可实现非失效机器人的降级重组,避免机器人之间发生碰撞;
2) 速度和加速度约束的引入,更符合实际情况参数更简单,且实现了控制算法的稳定与收敛;
3) 通过引入惩罚因子,使多机器人成功规避障碍,保持编队的同时搜寻出到达目标位置的最短路径,节省了运行时间.

