基于d-q变换的网侧双闭环谐波电流检测研究

陈泽华 马立新 李明江

摘要：有源电力滤波器大多采用基于瞬时无功功率理论的谐波检测算法。在运用该理论下的d-q算法时，由于使用到低通滤波器，使得谐波的实时提取精度较低并产生相移现象，当补偿低频次不平衡电流时难以控制输出的补偿电流分量。为了避免以上情况，提出了一种基于d-q变换的网侧电流双闭环控制谐波电流检测算法。以系统负载电流为干扰变量，网侧电流为状态变量，运用等式互消法建立以d-q坐标系为基础的网侧谐波检测模型。设计相应的电流、电压闭环控制器，避免因使用低通滤波器造成的补偿误差。仿真结果显示，新方法下的总谐波失真率比d-q变换减少了8.45%，低次谐波含量得到有效抑制。

关键词：APF;谐波检测;d-q变换;网侧电流;闭环控制

DOI： 10. 11907/rjdk.191389

开放科学（资源服务）标识码（OSID）：

中图分类号：TP319

文献标识码：A

文章编号：1672-7800（2020）001-0152-04

0 引言

新能源发展使得电力系统的电能质量问题变得越来越严峻[1]。与传统的无源滤波器相比，有源电力滤波器（ Active Power Filters，APF）拥有良好的隔离性能，能对不同大小和频率的谐波进行跟踪补偿，逐渐成为研究热点[2]，而APF需要产生频率较为丰富的高频正弦补偿电流。由于电网侧谐波电流的时变特性，故其补偿效果很大程度上取决于谐波电流的检测精度[3]。

目前，APF谐波电流检测技术主要采用日本学者Aka-gi提出的瞬时无功功率理论，以及由该理论所衍生出的p-q算法、ip-1q算法以及d-q算法等[4]。文献[5]在瞬时无功功率理论基础上增加了瞬时检测法，但计算量繁重且冗余度较大;文献[6]在ip-1q检测算法上结合了最小二乘系数，虽使谐波检测计算得到简化，但在电网电压波形发生畸变情况下，系统无法进行完整补偿;文献[7]将瞬时无功功率理论拓展到三相四线制上，但由于该方法中的功率以平均功率为准，检测电路比较复杂，不能满足谐波补偿的实时性要求。本文提出的网侧电流双闭环检测是在d-q变换基础之上的改进，实现d-q变换与闭环控制的优势互补，提高了APF的谐波补偿效果，缩短了响应时间。

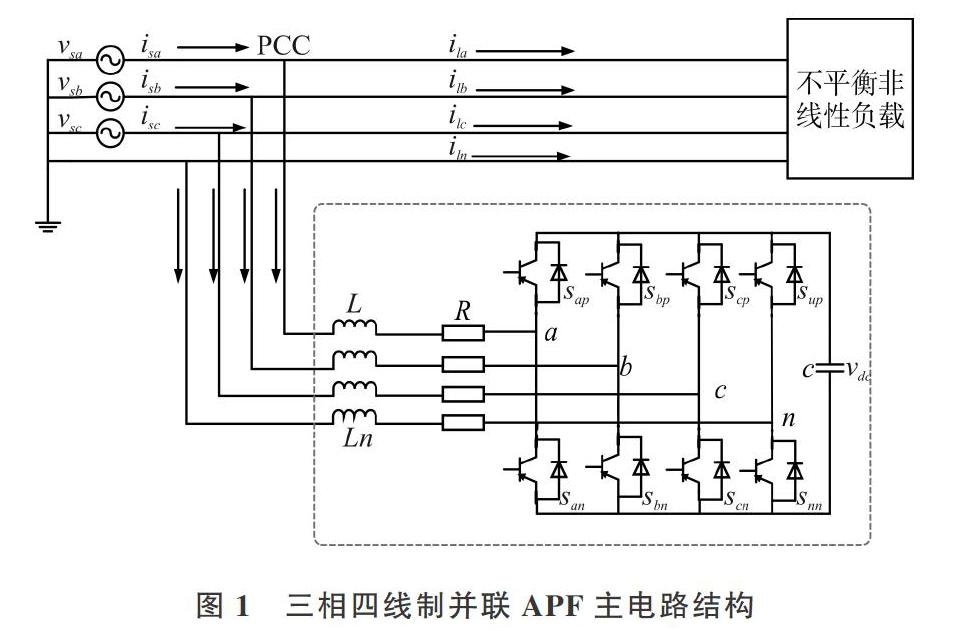
1 并联型APF系统结构

图1显示的是三相四线制并联APF主电路结构，其第4桥臂的作用是抑制配电网中的中性线电流[8]。R代表APF交流侧的等效电阻，L为等效电感，C代表APF直流侧的电容大小，Vdc是电容电压值。

在主电路结构基础上，APF在静止坐标系下的数学模型如下：

2 谐波电流检测方法

2.1 d-q变换谐波检测法

d-q谐波电流检测技术又称基于同步旋转坐标法[9]，其中的谐波检测单元负责检测出负载电流中的谐波电流大小，而APF据此参考电流生成与之大小相等的补偿电流，并反向输入到电网中。检测单元原理如图2所示，该单元检测出的负载电流从三相静止坐标系转换到dq0坐标系，再通过锁相环处理获得三相电源的相位信息，并当作旋转坐标转换的参考信号[10]。经过转换之后，负载电流中的基波正序有功电流变成d轴直流分量，基波正序无功电流就成了q轴直流分量，而其余次谐波电流在dq0坐标系上都变为波动分量[11]。当d轴直流分量通过低通滤波器（IPF）后，便得到基波有功电流，将它输入到三相负载电流中，两者相减就可获得最终所需要的补偿电流以及基波无功分量、谐波电流分量[12]。

但是在谐波检测单元中，LPF的滤波效果和响应速度往往互不相容[13]。当其降低截止频率提高滤波精度时，会延长APF的响应时间;相反，若要缩短响应时间，则又会恶化滤波效果[14]。除此之外，当APF采用d-q变换进行谐波电流检测时，产生的补偿电流由不同频率的正弦量合成。由于正弦电流随时间变化，在投射至dq0坐标系上时，系统的三相補偿电流便会失去原有的直流分量，使系统运行时缺乏鲁棒性[15]。

2.2基于d-q变换的网侧双闭环谐波检测法

为了解决以上弊端，本文对模型做出调整。主要以系统负载电流为干扰变量，网侧电流为状态变量，运用等式互消建立网侧谐波电流检测模型，并在此基础上设计出相应的电流、电压闭环控制器，构成以d-q变换为基础的网侧电流双闭环控制谐波检测体系。在系统的公共节点处，电流的相应方程如下：

图4中，网侧电流通过电流环控制器测量后，可得到谐波电流的参考信号，APF控制输出补偿电流使其跟踪此参考电流，并反向输入到系统负载电流中，从而达到抑制电网谐波电流，确保电流正弦化的目的[18]。与瞬时无功功率理论下的d-q变换相比，因检测系统中包含了电压、电流闭环控制器，故称为基于d-q变换的网侧电流双闭环谐波检测算法。

而从控制原理角度出发，d-q变换以负载电流作为控制变量并直接进行运算的方式属于开环控制法[19]。系统中的LPF会影响谐波电流的提取精度及稳定性，尤其当补偿低频次不平衡电流时会增加谐波检测单元的检测难度[20]。而以系统网侧电流作为控制变量，并通过电压、电流控制器直接计算的系统属于双闭环控制，其在进行谐波检测时，可以避免因使用LPF所带来的补偿效果差及相移等影响，在补偿低频次不平衡电流时，通过系统中电压控制器和电流控制器的相互组合，可以使系统稳定性更高，补偿效果更理想。

3 仿真验证

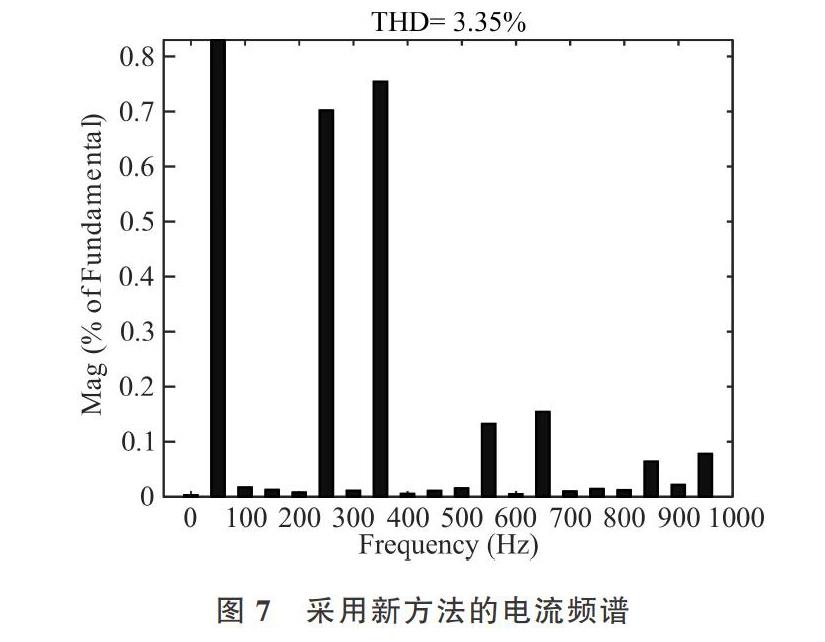
为验证新型检测算法的时效性，通过MATLAB仿真平台搭建相应模型并对该算法进行对比分析。图5是系统的三相负载电流波形，图6是采用d-q算法进行谐波检测后的频谱图。由图6（b）及图6（c）的电流频谱图可以看出，基于d-q算法进行谐波电流检测的APF在投入运行后，虽然谐波幅值得到显著降低，系统电流总谐波失真（THD）由原来的26.72%下降到11.8%，但补偿后系统中仍含有3次、5次、7次等大量其余次谐波。