从一类数学应用题的调查反思数学教育

刘宪升

摘 要 通过对物资调运类问题调查呈现出的事实，指出数学教育中大量的解题训练有可能使人的本能消失、思维受到严重束缚，失去其训练思维和应用的价值.

关键词 调查 解题训练 思维 应用

中图分类号：G424                                   文献标识码：A    DOI：10.16400/j.cnki.kjdkz.2020.05.068

Abstract From the facts revealed through investigations on material transportation issues， we point out that a huge number of problem-solving training in mathematical education may make people's instincts disappear， make their thinking be seriously restricted， and even make them lose their training thinking and applied value.

Keywords investigation; problem-solving training; thinking; application

作為普通高校的一名数学教师，我一直关注着中小学数学教育，从1997年起就对数学教育的一些问题坚持调查至今。目的是考察数学教育对学生思维的训练价值，及数学的应用价值和教育成效。下面，我们从一类数学应用题的调查谈起，然后做一些分析与反思。

1 物资调运类数学应用问题的调查

为了体现数学与生活的联系及应用，初中生学了一次函数后，关于物资调运省运费的问题便常以求最值的形式出现在课本、平时和中考试卷中。为方便讨论，我们先给出一道简单题目及其解法。

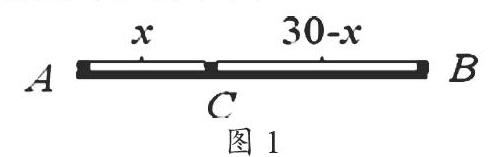
例1 某市、B两地相距30千米，每年各有3万吨、5万吨的物资需要销往外地。市政府计划在图1所示两地沿线上建一车站，使两地物资运往车站的总运费最省。问车站应建于何处？（运费单价：10元/吨、千米）

图1

解法一：设总运费为元。假设车站建在沿线上的地，离地千米（），则离地30-千米。由题意得：

∴

∵

所以，当时，取得最小值，总运费最小值是9000000元。

答：车站应建在离地30千米处。

可以说，与例1类似的题目，是应用一次函数解决的物资调运类问题中最简单的应用题，大多数学生用5～6分钟的时间就能求解出来。然而，这种机械的解法掩盖了问题是把一小、一大两堆东西堆到一起的实质。下面介绍该类问题的调查结果。

调查（一）——对不识字老人的调查。回农村老家时，我以场里有一小一大两堆麦子堆成一堆比较省劲的问题，询问过几十个没上过一天学的老人。他们都不假思索的说：“小堆往大堆堆啊！”有人还说：“从小就是这么干的，谁都这么干，你怎么问这样的问题？”言外之意说我读书读傻了。事实上，例1的结果就是把少的物资运往多的地方。

调查（二）——对民工的调查。有时走到一些工地上，我就对用小车推砂子（砖）的20岁左右的小伙子（至少有上百人），以一小一大两堆砂子堆到一起的问题调查，他们也是张口就说：“小堆往大堆推啊！”我说：“你们怎么不用初中一次函数求解出堆到哪里最省劲呢？”有的人说：“这问题一看就知道答案，用函数干嘛？”我说：“当时没把你的想法告诉老师吗？”他说：“我学习不好，不敢说，也怀疑自己的想法。”我说：“你的想法是对的，以后多点自信把本能发挥出来。”

调查（三）——对幼儿园大班孩子的调查。借与朋友相聚的机会，我调查过三十多个五六岁的孩子。考虑到他们的理解力，就在桌子上摆上明显大小不同的两堆瓜子或糖块，让他们用最省劲的办法把这两堆堆成一堆，做对了就送给他们吃。结果，孩子们的小手嗖的一声就把小堆推到了大堆上。

调查（四）——对中小学生的调查。利用带学生实习的机会，我拿此类问题调查过起码有几百个中小学生。结果，没学过一次函数的小学、初中学生都很快的解决了问题;而学过的初高中生都是用一次函数来求解，且不给出两地之间的路程和运费单价就说少条件，求不出具体地点来。

调查（五）——对大学生的调查。利用给学生上课的机会，我拿此类问题调查了不说上万也有几千个大学生。其中，数学专业的学生每级每个班都调查过（我都上过课）;公选课上几乎调查了我校各个专业的学生。拿例1来说，当不给出两地间的路程和运费单价时，学生都说少条件。当补上路程和运费单价时，他们说用一次函数就可求解。我说假设建在离地（少的地方）的路程是千米，列出函数关系式并求出结果告诉我具体地点，结果都说建在离地30千米的地方，就是不说建在物资多的地。

另外，我还借与不少中小学及大学老师交流的机会，简单的询问过这类问题。结果也是说用一次函数求解。这从老师们布置的练习题，课本及考试题中常有类似题目可佐证调查结果是符合实际的。

其实，在例1中我们用一次函数给出的解法，无非是证明了人们本能的做法是对的、是科学的。另外，若能引导学生动脑思考，亦可简单的给出其解法。

解法二：因不管车站建在间沿线上的那一个地方（含），将两地物资运到车站的总路程都是30千米，故运的物资越少越省钱，所以把处的物资运到处，车站应建在地。最少运费为：30000？0？0=9000000（元）。

有人可能说这个问题太简单，难一点的行吗？其实，为了充分体现一次函数的应用，增加难度，课本和中考题中就出现了很多两地往两地调运物资的问题。我们以人教版课本[1]上的复习题为例进行说明。

例2 城有肥料200t，城有肥料300t。现要把这些肥料运往两乡。从城往乡运肥料的费用分别为20元/t和25元/t;从城往乡运肥料的费用分別为15元/t和24元/t。现在乡需要肥料240t，乡需要肥料260t。怎样调运才能使总运费最省？（配图略）

分析：因从两城运往乡的费用分别是20元/t和15元/t（最低），每吨差5元;运往乡的费用分别是25元/t（最高）和24元/t，每吨差1元。故应将城肥料尽量多（城尽量少）的运往乡，不够的再从城运;若城肥料多于乡需要，多出来的就运往乡。

解：调运方案为：从城运往乡240t，运往乡60t;城运往乡0t，运往乡200t。此时总运费最省，最少运费为：240？5+60？4+200？5=10040（元）。

此题若用一次函数求解（略）得十几分钟，可略一动脑就能简单的解决。可见，凭本能或略加思考就可解决的问题，得到上述调查结果令人痛心。

2 分析与反思

2.1 要实现数学训练学生思维的教育价值仍有待研究与努力

（1）大量的解题训练有可能致使人的本能消失。对于该类问题，若说老人由于生活经验的积累悟出了道理，可幼儿、小学低年级的学生的做法除了人都具有解决这一类问题的本能外，我想不出其他解释。可学过的人，尤其是学得“好”的人，为什么不知道小堆往大堆堆呢？个中原因除了大量的解题训练有可能致使人的本能消失，还有其他原因吗？

（2）大量的解题训练严重束缚学生的思维。按说学习好的人解了大量的这类问题，理应能认识其实质，可为什么认识不到呢？这是因为，学生学习数学大都靠大量的解题训练和机械的套模式来提高成绩，甚至连“答”都是机械式的。这导致了学生解题后不进行比较与思考，更甭说质疑，失去了认识实质的机会。甚至严重束缚与禁锢了他们的思维，且束缚可伴随人几十年或终生，成了戴在头上的“紧箍咒”。

众所周知，数学享有思维体操的美誉，具有训练思维、开发智力的教育价值。由上可见，这种价值要实现还是有待数学教育工作者的研究与努力。

2.2 要实现数学的应用价值仍有难度

这些年来，虽然课本编写及老师的教学都注重了数学与生活的联系和应用，但由上可见，不仅解法有玩数学游戏的感觉，问题本身也有游戏性质。如在例2课本上的配图中，城比城离乡近，但运费单价却每吨多5元;城离乡比乡远，可运费单价却每吨少9元。这不违背常理吗？若把这问题搬到生活中去岂不闹出天大的笑话。事实上，类似这样严重脱离实际的应用题屡见不鲜，问题本身不符合实际怎能让学生体会数学的应用，通过这样的问题讲应用很难现数学的应用价值。

综上所述，数学教育的价值重在训练思维和实际应用，但靠“题海战术”，多讲多练，要达成目的是有困难的，会使数学的教育价值大大折扣，甚至可能影响学生的发展。因此，作为数学教育工作者应在反思的基础上好好研究一番，为祖国的后代开启一片光明未来。

参考文献

[1] 人民教育出版社，课程教材研究所.义务教育教科书·数学（八年级下册）[M].北京：人民教育出版社，2013：109.