互联网背景下外卖配送保险定价理赔模型的构建

邓芷珊 王陈丽

摘 要：外卖业在近年蓬勃发展，但外卖丢失事件的发生给配送员带来了巨大的财产损失，而我国保险业在该领域尚为空白。本文基于成本等于收益原则，结合二叉树模型，制定了互联网背景下外卖丢失损毁险的算法框架，分析费率因子及其权重，对骑手的丢单风险进行评分，确定不同风险类别下的骑手理赔策略。最后利用状态转移矩阵给出了理想假定下的保费算法优化方案。本模型弥补了外卖配送保险领域的空白，对促进外卖送餐行业可持续发展具有重要意义。

关键词：外卖配送保险  风险评分  状态转移矩阵

1 问题背景

自1980年我国恢复国内保险业务以来，财产保险业迅速发展。经过“十一五”时期的发展，我国财产保险业整体实力明显提升，行业风险得到有效防范，服务经济社会的能力进一步增加。经过几年来的治理，财产保险市场秩序也有了明显好转。但是，在外卖送餐过程中发生的大量外卖损毁被盗等意外事件说明，外卖服务行业仍存在有待开发的财产保险的市场空白;同时，目前小额财产保险处于需要进一步探索和拓展的阶段。

由于外卖订单金额与配送员每单提成间存在巨大的差距，外卖一旦丢失损毁，配送员将承担巨大损失。此外，调查显示，67%以上的受访者曾经历或听闻外卖丢失事件，80%以上的受访者认为配送员对该类保险存在一定需求。根据数据显示，中国有8.29亿互联网用户，其中使用外卖服务的用户高达4.21亿，所以依托外卖服务所形成的庞大立体的本地即时配送网络的发展完善十分重要。因此本文将探索小额财产保险的新型领域，以外卖丢失损毁险填补外卖险种的空白。

外卖配送保险是针对外卖配送员推出的一款保险产品，旨在通过对保险金额补偿为外卖送餐者提供更多的财产保障，减少他们因外卖被盗而产生的损失。通过对外卖配送员每日送餐单数、外卖送餐每单金额、外卖配送区域集中程度等客观影响因素，以及外卖配送员好评率等主观影响因素的调查分析，利用二叉树定价模型、泊松模型等数学工具计算保险费用、赔偿金额，为“外卖配送保险”作出科学定价。以外卖平台为媒介，既保障了外卖配送员的利益，也优化了外卖平台的配送流程，实现双赢。“外卖配送保险”在一定程度上填补了外卖配送服务领域中的空白，并且能够达到为送餐从业者提供更多财产保障的目的。这将有效地促进外卖送餐行业的发展，让更多的从业者在送餐过程中得到保障、减少损失，留存和吸引更多的人从事这一行业。总的来说，“外卖配送保险”对促进外卖送餐行业积极可持续发展具有重要意义。

2 模型构建

2.1 定价基本原则

首先假定外卖配送保险的有效期为一年，时间较短，因此不将利率因素纳入考虑范围。定价模型应符合收入不小于支出的原则，即所有配送员所交保费之和大于等于保险公司赔付总金额与公司运营该保险成本之和。可以得到以下不等式：

由于财产保险和期权本质上都是一种避险工具，在很多方面具有相似性，因此本文将二叉树模型运用到外卖现保费定价中。表示股票价格上涨时投资者拥有的资金总量，表示股票价格下跌时投资者拥有的资金总量，股票的初始价格，表示股票的初始价格，代表1时刻的股票价格，表示所购买的股票份数，r表示无风险货币市场的利率。根据二叉树模型的公式如下：

这里，令外卖的平均价格为，完好送达购买者处时价格為。如果外卖完好地送达购买者，则有;如果外卖被偷或损坏（损坏已导致外卖无法正常食用），则有，即

假设外卖险提供的赔付金额为，在出现赔付的情况下配送员所得价值为。根据二叉树模型和无套利平衡的原则可得，保费价格为。由于，从而得到，其中表示丢单量与外卖总量的比值。因此，我们提出的定价模型基本原则得到论证。在本文对定价模型的讨论中，假设当支出达到最大值时该不等式取等，并以此作为讨论对象，即

2.2 定价模型构建

2.2.1 风险评分

假设经考察，确定影响配送员外卖丢单量的三个主要因素为：配送员接单量、配送员的配送区域、配送员好评率。因此，可以进一步将这三个主要因素作为对配送员丢单风险评分的三个指标，将指标进行标准化消除量纲对评分的影响后，分别记为。在此基础上构造多元总体线性回归函数为：

而外卖丢单量与配送员的接单量、配送区域呈正相关关系，与配送员的好评率呈负相关关系，可知。于是配送员丢单的风险与其风险评分成正相关关系，即丢单风险越大，值也就越大。

2.2.2 聚类分析与泊松过程

在所有参保配送员中进行随机抽样，得到一个容量为（）的样本。确定将该样本分为9类，根据风险评分指标采用K均值法进行聚类分析，得到分为9类的聚类结果。

泊松分布适合于描述单位时间（或空间）内随机事件发生的次数，因此不妨假设每个配送员在一年中的索赔次数服从泊松分布且独立同分布。对于聚类结果的第类，类中每个配送员的平均年丢单量为：

其中，表示第类所有配送员的丢单总量，表示属于第类的配送员人数。而泊松分布的数学期望等于其参数，可进一步假设第类中每个配送员的年丢单量服从参数。

2.2.3 指标修正

记录样本中所有配送员第一年的索赔次数，记第类中的第个配送员在第年为，即其在第一年中的索赔次数为，则该配送员第二年索赔次数的期望为：

根据该配送员第二年索赔次数的期望，对该配送员的三个风险评分指标进行修正，即

并由此得到修正后的风险评分值

于是，在第二年年初根据每个配送员修正后的风险评分指标采用K均值法重新进行聚类，并分为9类。此后每一年都重复上述的计算，反复修正风险评分指标和风险评分值，并以此为根据重新聚类。对于新加入保险的投保人，在首次得到其风险评分指标值后同样通过聚类的方式将其进行分类，此后按照上述流程进行处理。

2.2.4 计算投保费用

根据定价基本原则，即

在已知每年赔付总金额与公司运营该保险成本之和的最大值的情况下，得到外卖险需要收取的总投保费用。再由每位投保人（配送员）的风险评分值为系数，按比例计算得出应向该配送员收取的投保费用。

3 理想假定下的保费算法优化——基于DTMC模型的实例探讨

在原始模型中，我们对于不同风险等级的配送员进行不同赔率的赔付，而所有的配送员收取相同的保费;在修正后的模型中，我们对不同等级的配送员进行不同的保费收取，而进行相同的赔率赔付。这一修改的优势在于，减少了方程中的未知数个数，便于保费的计算。

定义配送员所处的类型为配送员的状态，在参保者不发生变化的情况下，配送员状态的转移过程具有马尔可夫性，可使用DTMC模型。即在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的。换言之，配送员去年的丢单量影响今年所处的状态，今年的状态反映了上一年的丢单量。并且，配送员在不同状态之间的转移是存在一定概率的，用状态转移概率矩阵进行刻画：

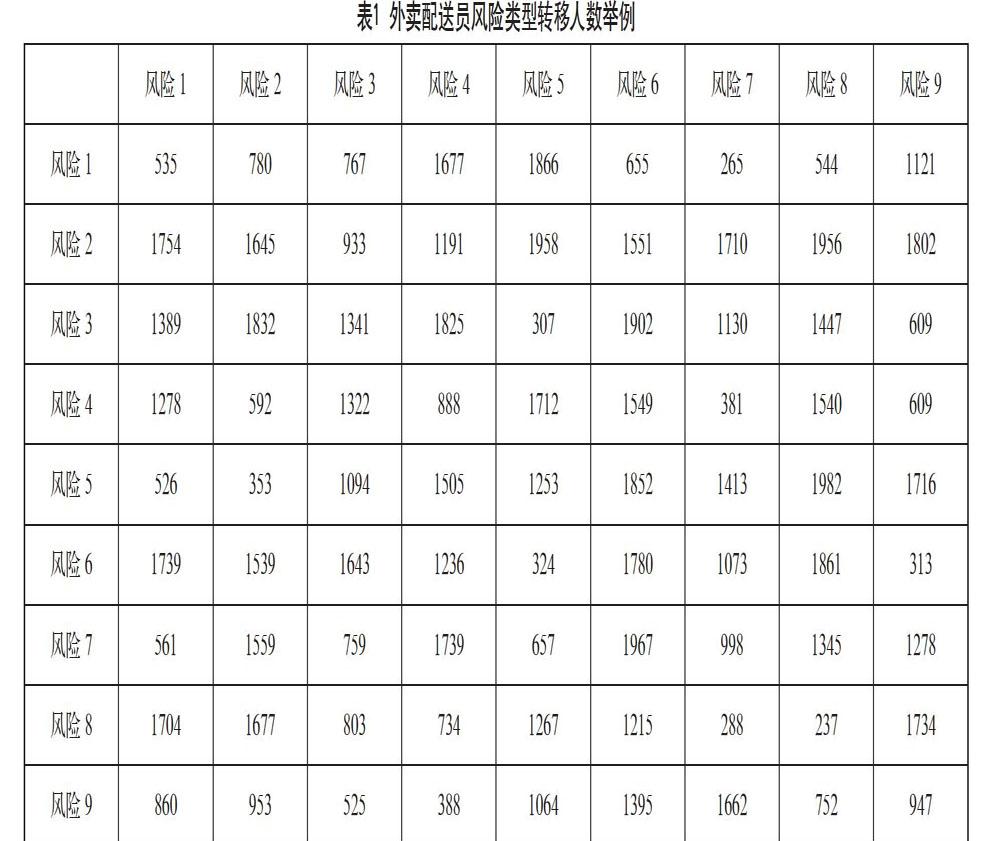
其中， Pij表示从i状态转移到j状态的概率，以P11为例，通过调查连续两年都处于1状态的配送员数量，计算其占所有配送员的比例，得到P11。例如，表1列举了一种从某一风险到另一风险类型转移的配送员数量，其中风险1表示风险最低状态而风险9表示风险最高状态。

假定各年的状态转移情况在数据量足够大的情况下相同，则所得到的状态转移概率矩阵可以直接用于计算下一年处于各状态的配送员数量，从而利用收益最大成本等式计算每类配送员的保费。该方法的优势在于避免了每年记录配送员的费率因子参数值和聚类分析，大大减少了计算量。当然，实际中各年的状态转移情况可能不同，参保者也可能发生变化，本方法可能并不适用，但确实为该问题的解决从理论层面上提供了思路。

4 结语

外卖业飞速发展，而外卖丢失事件却层出不穷，这为本文探讨外卖配送险提供了理论基础与现实意义。本文选定配送员接单量、配送员的配送区域、配送员好评率作为风险因子，衡量配送员丢单风险，利用多元线性模型制定了配送险保费算法基本框架。在互联网背景下，容易得到各配送员的风险因子取值，从而计算丢单风险评分，确定保费。本文提出的算法模型在一定程度上可弥补该领域的保险空白，对分散配送员风险，促进外卖送餐业健康持续发展具有一定意义。

参考文献

王世琼，张文姣.大学生外卖存取情况调查研究[J].现代商业，2019（30）.

朱良成.简评期权定价思维和保险精算思维的相互关系[J].新经济，2014（Z1）.

連锦泉.财险公司产品市场定价模型研究[D].厦门：厦门大学，2004.

李亚.非寿险精算的数理统计应用[D].武汉：华中师范大学，2015.