基于TMD的大跨连续钢箱梁人致振动分析研究
蒋星宇,卢江波,周旺保
(1.湖南省交通规划勘察设计院有限公司,湖南 长沙 410219; 2.中南大学 土木工程学院,湖南 长沙 410075)
0 引言
与常规的混凝土结构相比,钢结构具有质量轻、强度高的优越性能,同时,钢材能够进行工业化批量生产、施工快捷高效且质量高,在经过合理的表面防腐后,钢结构的耐久性能明显高于混凝土结构,因此,在桥梁跨径大、桥型复杂以及对景观有较高要求时,钢结构桥梁可作为一种选择方案[1]。国内已有不少景观人行桥选择钢结构作为最终设计方案,但当人行桥的跨径较大时,钢结构存在结构刚度较小的问题,有时可能不满足《城市人行天桥与人行地道技术规范》(CJJ69-95)(以下简称规范)第2.5.4条的要求[2],即结构的竖向自振频率不应小于3 Hz。《规范》2.5.4条是从减小行人的不安全感出发而作此规定,事实上,行人的不安全感或不舒适感与结构在人群动荷载作用下结构最大加速度响应幅值相关,只要加速度最大响应幅值在一定范围内,不安全感或不舒适感都可接受,德国的人行桥设计指南(EN03-2008)[3](以下简称设计指南),即以加速度峰值作为设计控制指标; 另一方面,对于现代大跨轻型人行桥,受设计合理性与有效性限制,很难做到结构竖向自振频率不小于3 Hz[4-5],因此《规范》2.5.4条存在不合理性。目前对于与《规范》2.5.4条相冲突的钢结构人行桥,一般采取添加调质阻尼器(TMD)来控制结构在人行荷载作用下的加速度响应,以便满足行人的安全感和舒适感。本文将对一座大跨变截面连续钢箱梁人行桥(跨径组合58.6 m+110 m+58.6 m)进行人致振动分析,并提出优化的TMD设计方案,确定合理的减振控制方案。研究结果可为我国有关规范的制定及类似大跨连续钢箱梁的减振控制分析提供重要参考。
1 人致振动控制基本原理
控制人致振动主要有2种方法,一种方法为调整结构的刚度和质量,使其结构自振频率不在人群动荷载典型频率范围内,避免共振;一种方法为提高结构的整体阻尼以减小结构在人行荷载下的共振响应。增加阻尼的方法有多种,其中最经济有效的方法为安装阻尼系统,常用的有粘滞阻尼器和调质阻尼器(TMD),前者能够提高多阶模态的阻尼,但是阻尼器两端会有较大的相对位移,后者能够显著地提高相关模态的阻尼比,应用较为广泛[6-10],本文即采用TMD来进行人振振动控制。
TMD系统由质量块、弹簧和阻尼器组成,通过调整质量块的大小以及刚度可使TMD系统的固有频率接近主结构的某阶自振频率,当主结构受到振动时,TMD系统就会产生一个与主结构振动方向相反的惯性力作用在主结构上,使结构的振动减弱。单自由度结构添加TMD系统的模型如图1所示,其运动方程如式(1)所示。
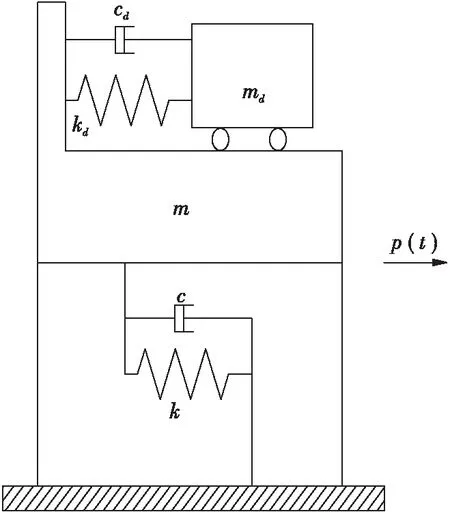
图1 结构-TMD耦合系统模型

(1)
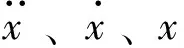
TMD 的最优参数设计因控制目标不同而不同,在人行桥领域,结构的加速度响应是控制目标,因此采用最大加速度最小化作为控制目标。通过优化设计,可得TMD的最优频率和最优阻尼比为[6]:
(2)
式中:βopt=fd/fs为TMD系统的固有频率fd与结构的频率fs的比值;μ=md/m为TMD 系统的质量与结构的质量之比;ξopt为TMD系统的最优阻尼比。
2 大跨变截面连续钢箱梁动力特性分析及其人致振动舒适性评价
2.1 工程概况及计算模型
本文背景工程为一座主跨110 m的变截面连续钢箱梁人行桥,跨径组合(58.6+110+58.6)m,截面为单箱单室,如图2所示,中支点、边支点以及第2跨跨中梁高分别为5.3、2.4、2.8 m,采用2次抛物线过渡,箱梁顶面总宽9.6 m,主梁采用Q345qC。
采用MIDAS2019建立变截面连续钢箱梁模型,截面采用钢梁截面,纵向加劲肋直接在截面中考虑,横向加劲肋以荷载形式考虑,2期恒载以荷载形式添加,并将恒载转换为质量进行分析,有限元模型如图3(a)所示,全桥共167个节点,157个单元,一般支座约束横向和竖向以及绕桥纵向的扭转,左起第2个支座增加纵向约束和绕桥竖向转动,如图3(b)所示。
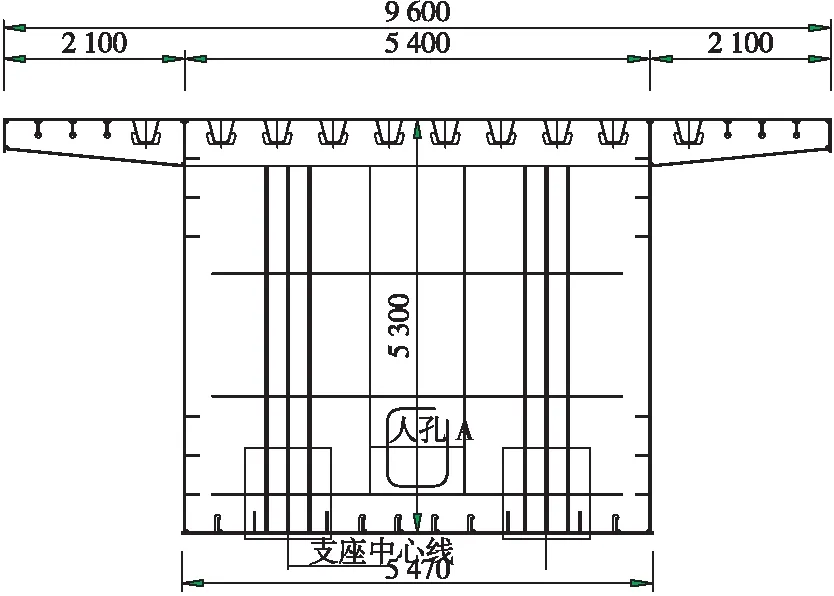
(a)中支点截面

(a)有限元模型
2.2 结构动力特性
通过模态分析,人行桥的前10阶模态,其振型频率和主要振型描述如表1所示。根据设计指南中考虑步行频率的等效荷载折减系数规定,如图4所示,选取第1~第5阶模态按设计指南给出的计算方法分析主梁的竖向和横向加速度响应,并进行舒适性评价,第1~第5阶的振动模态如图5所示。

表1 人行桥前十阶模态的振型描述Table1 Modeshapedescriptionofthefirsttenmodesofthefootbridge模态号频率/Hz主要振型描述11.114一阶竖弯(正对称)22.266一阶侧弯32.388二阶竖弯(反对称)43.201三阶竖弯(正对称)54.244四阶竖弯(反对称)64.862二阶侧弯75.393五阶竖弯+纵漂86.123三阶侧弯96.517四阶侧弯106.808六阶竖弯(正对称)

图4 考虑步行频率的等效荷载折减系数
2.3 舒适度评价
从表1和图4可以看出,人行桥第1阶频率1.114接近敏感频率1.25,第3阶频率2.388接近2.3,偏安全的,本次分析考虑第1阶频率和第3阶频率的影响,其折减系数均取1,第4阶和第5阶模态取0.25,其余取0,侧弯模态(第2、6、8、9阶)频率都不在敏感频率0.5~1.2 Hz范围内,折减系数为0,不考虑。设计指南规定的等效人群荷载如式(3)所示,单位为N/m。

(a)一阶竖弯(正对称)
Pr(t)=P0×cos(2πfr×t)×d′×Ψ
(3)
式中:P0为步行力峰值,竖向、纵向和侧向步行力峰值分别为 280、140、35 N;fr为第r阶模态频率;Ψ为折减系数,其值反应了行人步频同步的可能性,其值大小与步行频率相关,范围为 0~1,折减系数取值如图4所示;d′为等效人群密度,取值如下所示:
当人群密度d<1.0人/m2时,
(4)
当人群密度d≥1.0人/m2时,
(5)
式中:S为人行桥人行道面积,S=B(人行道宽)×L(人行道长);n为设计人群总数,n=d×S,人群密度本文取0.5人/m2;ξ为阻尼比,对于本文中的钢结构人行桥取0.5%。
按式(3)计算得各模态下的等效人群荷载按振型施加于模型上,加载时,步行力荷载按增大振幅的方向加载,如图6所示,根据在人行荷载作用下的振动加速度响应,进一步按设计指南对人行桥的加速度和舒适性进行评价,评价结果如表2所示。从表2可以看出,人行桥第1阶及第3阶频率的的竖向最大加速度幅值大于0.5 m/s2,不满足设计指南中规定的最舒适性要求,需要采用有效的减振措施。
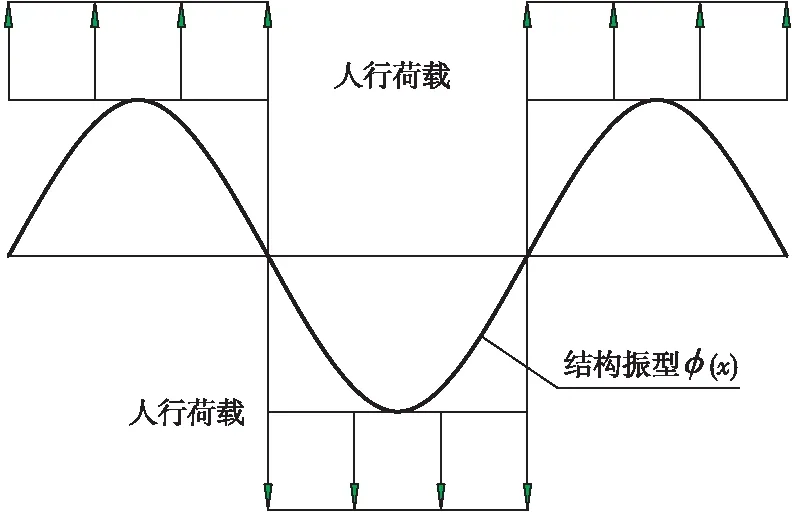
图6 步行荷载根据振型φ(x)加载

表2 人行桥相关模态下的最大竖向加速度和舒适性评价Table2 Maximumverticalaccelerationandcomfortevaluation模态号频率/Hz最大竖向加速度/(m·s-2)舒适性评价11.1140.638中等32.3880.546中等43.2010.166最好54.2440.145最好
3 基于TMD的振动控制及参数分析
3.1 TMD参数分析
根据TMD的最优频率和最优阻尼比公式,首先需确定合适的质量比,然后才能确定TMD系统所需其它参数。下面以第一阶模态为例,质量比μ取0.1%~1%,该阶模态的模态质量为420 966 kg,固有频率为1.114 Hz,不同质量比TMD系统的相关参数如表3所示,其中TMD系统仅布置中跨跨中位置,该位置振型位移最大,布置在该位置,减振效果最好。
结构最大加速度及减振率随质量比变化的规律如图7、图8所示,从图7可以看出,结构的最大加速度随着质量比的增大先急速下降,随后趋于平缓。图8的减振率变化规律显示,质量比为0.1%时,结构最大加速度的减振率即接近75%,与图7显示规律一致,随着质量比的增大,减振率越来越平缓。综合考虑经济性、舒适性以及TMD系统制作标准化(本桥单个TMD装置的有效运动质量均设为1 000 kg),第一阶模态的质量比取0.475%,质量为2 000 kg,此时结构最大加速度为0.086 m/s2(减振率达86.5%),满足设计指南中规定的最舒适性要求。

表3 第1阶模态TMD系统最优参数表Table3 OptimalparametersofTMDsystemforthefirst-or-dermodal质量比μ频率比βopt阻尼比ξopt质量/kg弹簧刚度/(N·m)阻尼系数/(N·S·m-1)0.10%0.99950.0194421206011140.20%0.99900.0274842411603220.30%0.99850.03351263616795920.40%0.99800.03871684821579100.50%0.99750.0432210510259412710.60%0.99700.0474252612299016700.70%0.99650.0511294714334621020.80%0.99600.0547336816366225670.90%0.99550.0580378918393730601.00%0.99500.061142102041723582

图7 结构最大加速度与质量比的关系
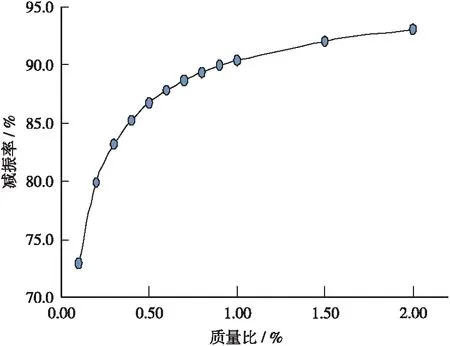
图8 结构最大加速度减振率与质量比的关系
3.2 TMD设置方案
第1阶模态的TMD布置在第2跨跨中位置,TMD有效质量与第1阶模态质量的比值为0.475%(TMD重2 000 kg),第3阶模态TMD布置在第1跨跨中、第2跨1/4跨、第2跨3/4跨以及第3跨1/4跨位置,其总的质量比为0.620%(TMD重4 000 kg),所有TMD系统布置如图9所示。人行桥加TMD前后,第1阶模态和第3阶模态的最大加速度时程如图10所示,可以看出,加TMD后,结构的最大加速度减小非常显著,第1阶减至0.086 m/s2(减振率86.5%),第3阶减至0.075 m/s2(减振率86.3%),加速度峰值均满足设计指南中规定的最舒适性要求。
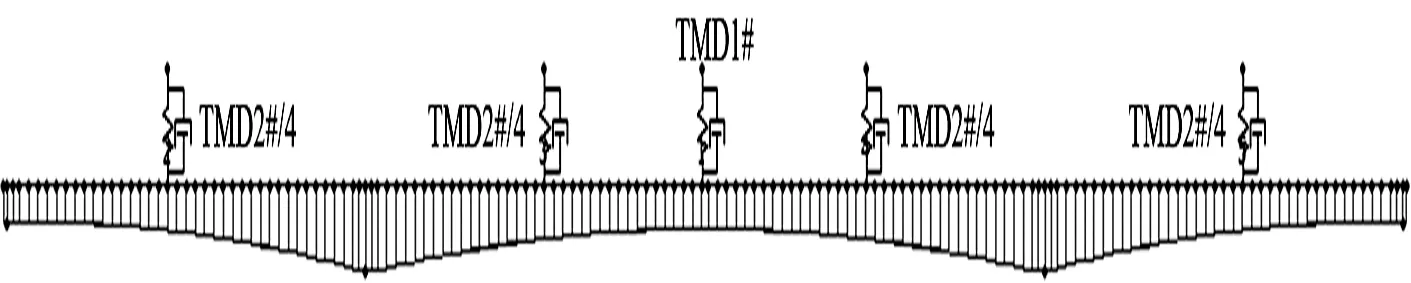
图9 人行桥TMD布置
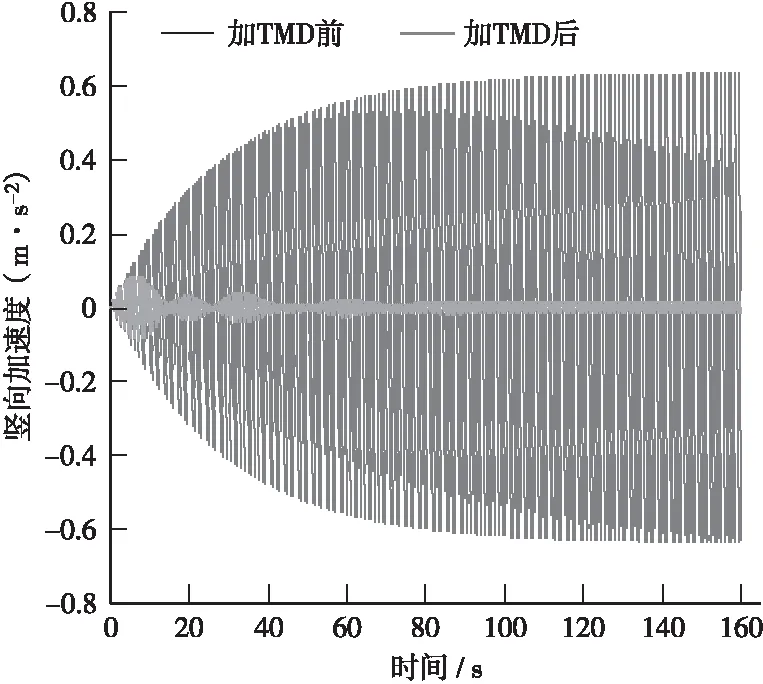
(a)1阶模态中跨跨中加速度时程
4 总结
a.我国规范对人行桥竖向自振频率的要求过于严苛(不应小于3 Hz),目前大跨变截面连续钢箱梁人行桥难以满足,若强行满足则设计会不合理,设计指南以结构在人行荷载下的加速度幅值为指标评价对结构的人致振动舒适性进行评价,指标明确合理,具有很强的可操作性,可做为大跨变截面连续钢箱梁人行桥的动力设计的重要参考。
b.采用TMD能够有效地控制结构的人致振动响应,如对本文人行桥第1阶模态人致振动响应的抑制,TMD有效质量与第1阶模态质量的比值为0.1%时,结构竖向加速度减振率即接近75%,但是,随着这一比值的增加,减振率越于平缓,减振效果越来越不明显,同时,当TMD系统质量较大时,安装不便,对原结构的受力性能亦有影响,因此需要综合各方面因素,确定合适的质量比。
c.对于本桥,通过在各阶模态的最大振型位移处布置总重为6 000 kg的TMD系统,即满足了设计指南所规定的最舒适性要求,减振率在86.3%以上,同时也不会对原结构有较大影响。

