基于MATLAB的胶囊内窥镜驱动机器人的运动学分析及仿真
陈 曦,俞经虎,钱善华,曹 澍,胡雨农
(1.江南大学机械工程学院,江苏 无锡 214122)(2.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
传统的消化道类疾病的诊疗方法多为机械侵入式,例如肠镜、胃镜等,这种方式会给患者带来不适感,使患者产生抵触情绪逃避检查,并且有可能造成新的损伤。近年来,随着科技水平的不断提高,特别是MEMS(微机电系统)技术的发展,使得无创手术与传统手术相比有着更明显的优势。胶囊内窥镜作为胃肠道疾病的新型检查方式,逐渐取代了传统的插入式胃肠镜诊疗方式,这种无创检查方式大大减轻了患者的不适感。
2010年,意大利Gastone Ciuti等[1]针对优化结构、精确和可靠性等目标完成了一个更紧凑的设计,使用6自由度串联机械手来支持永磁体实时控制胶囊内窥镜;2015年,意大利Gioia Lucarini等[2]提出用一种新型的环形电磁铁作为控制和驱动系统,该系统结合了电磁铁的优点及机器人操纵的灵活性。2010年,华中科技大学的高鸣源[3]提出了一种新型磁控导航系统,该系统共有5个联动轴,可以实现胶囊在肠道内的快速运动、缓慢运动和局部定位等;2016年,上海安翰医疗技术有限公司[4]研发出NavicamTM胶囊内窥镜机器人系统。
医疗器械的快速发展对空间技术的要求进一步提高。本文提出了一种结构为三移两转的串联机器人来实现胶囊内窥镜对人体的诊疗。诊疗过程中,串联机器人执行末端带动磁球移动,实现胶囊内窥镜的转动、前进与转动前进复合运动,医生通过控制驱动机器人,可以实时观察胶囊内窥镜传回的图像,对病变部位进行靶向定位施药,甚至可以完成手术操作等等。驱动机器人可以在一定程度上让胶囊内窥镜的驱动方式更加高效、精准。
1 驱动机器人的总体设计
1.1 驱动机器人结构
在诊疗过程中,该机器人通过3个移动自由度和2个转动自由度实现对磁球的控制,进而达到对人体内具有磁性的胶囊的定位和姿态控制,完成胶囊转动、前进与转动前进复合运动等一系列运动。胶囊驱动机器人的结构如图1所示。
图2为驱动机器人的结构示意图,由图可见驱动机器人固定在底座上,由移动副和转动副共同组成。该驱动机器人为实现控制磁球运动的串联驱动结构,其中移动运动分别由各方向的伺服电机带动丝杠沿各自导轨滑动,实现沿X,Y,Z方向的线性传动,转动运动分别通过伺服电机控制实现绕Z轴方向的旋转(θ4)和绕磁球围架轴线的旋转(θ5)。
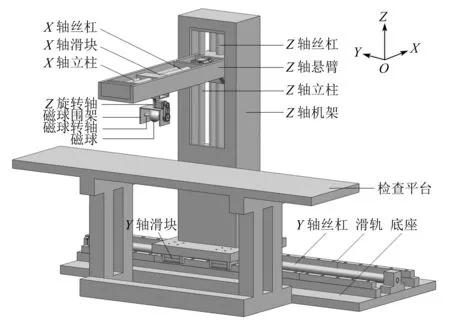
图1 驱动机器人三维模型
1.2 机械手位姿描述
描述驱动机器人的位置和姿态是对其进行运动学分析的基础,在传统的笛卡尔坐标系中D-H矩阵可以精准快速地建立串联机构的坐标模型,因此本文采用改进后的D-H法[5]确定各部分的位姿和相对运动关系。图3中移动副互相垂直,运动范围分别是d1,d2,d3。转动副的轴线互相垂直,旋转范围分别为θ4和θ5,点O5为末端运动点。简化后各连杆坐标系如图3所示,相应结构参数见表1。
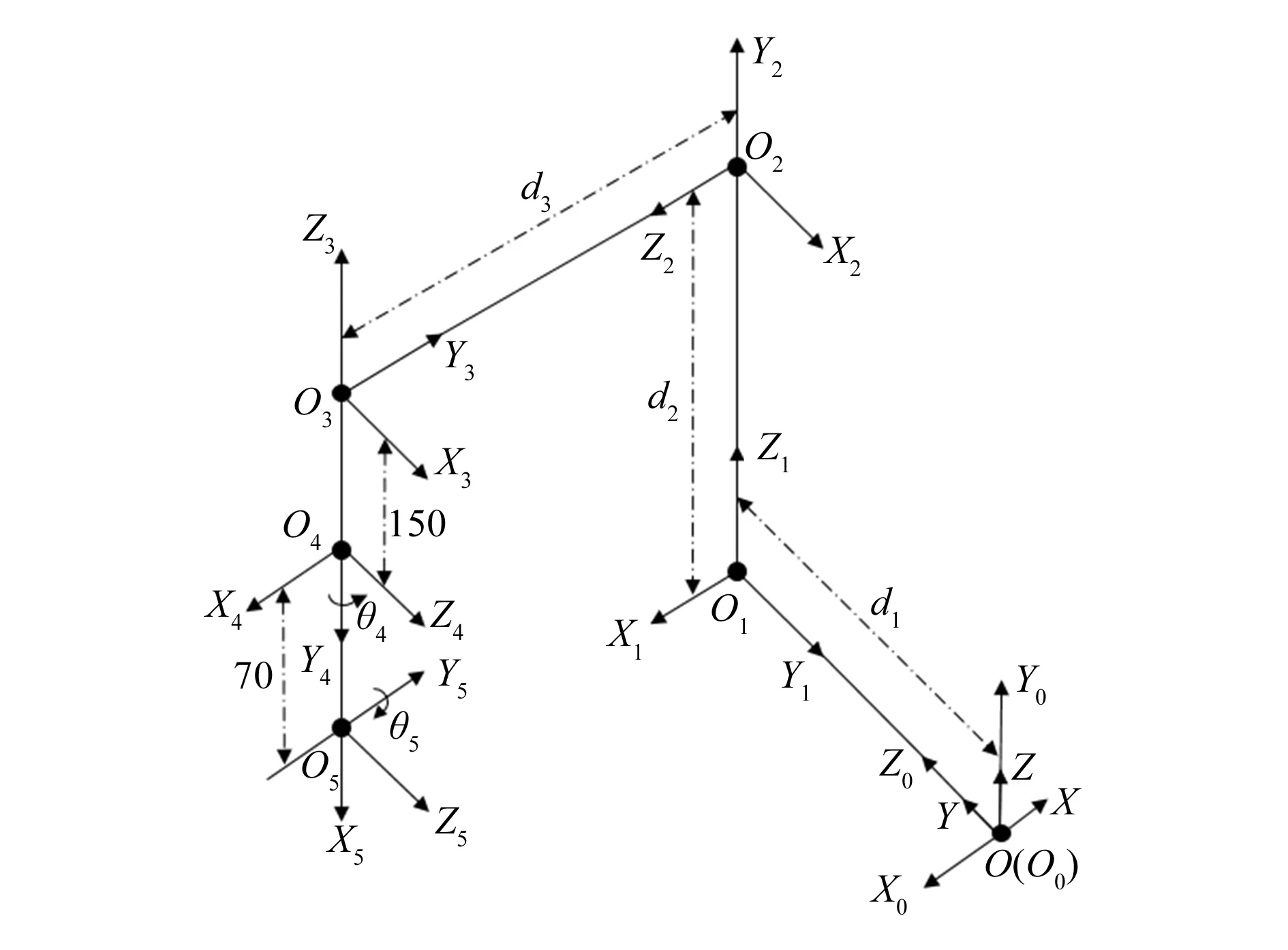
图3 驱动机器人D-H坐标系

表1 驱动机器人的D-H参数表
表中,θi为Xi-1到Xi绕Zi-1旋转的角度;di为沿Zi-1方向Xi-1到Xi的距离;ai-1为沿Xi-1方向Zi-1到Zi的距离;αi-1为Zi-1到Zi绕Xi-1旋转的角度。为了使计算结果清晰明了,建立基坐标系O-XYZ和机架坐标系O0-X0Y0Z0,以导出相关运动学方程。
2 驱动机器人的运动学分析
运动学分析在机器人的研究过程中有着举足轻重的作用,可以确定机器人手臂位置、姿态以及各相邻关节位置的对应关系[6]。运动学分析包括两类:一是正运动学分析,给定各个连杆关节变量,求解相邻连杆之间以及机械手末端位姿;二是逆运动学分析,给定机械手末端位姿,求解各个连杆关节的变量值。
2.1 正运动学分析
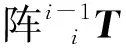
(1)
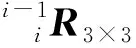
(2)
式中:n,o,a均为旋转矢量;p为平移矢量。
将表1中的D-H参数代入式(1),可得
(3)
将式(3)代入式(2)得:
(4)
式(4)中,c4表示cosθ4,s5表示sinθ5,以此类推。将各关节已知变量代入驱动机器人的运动学方程式(2)中,便可得到驱动机器人末端坐标系O5-X5Y5Z5相对于基坐标系O-XYZ唯一的准确位姿矩阵。
2.2 逆运动学分析
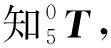
(5)
由式(5)可以求得:
(6)
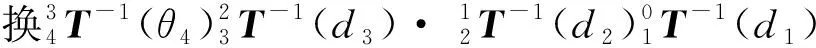
(7)
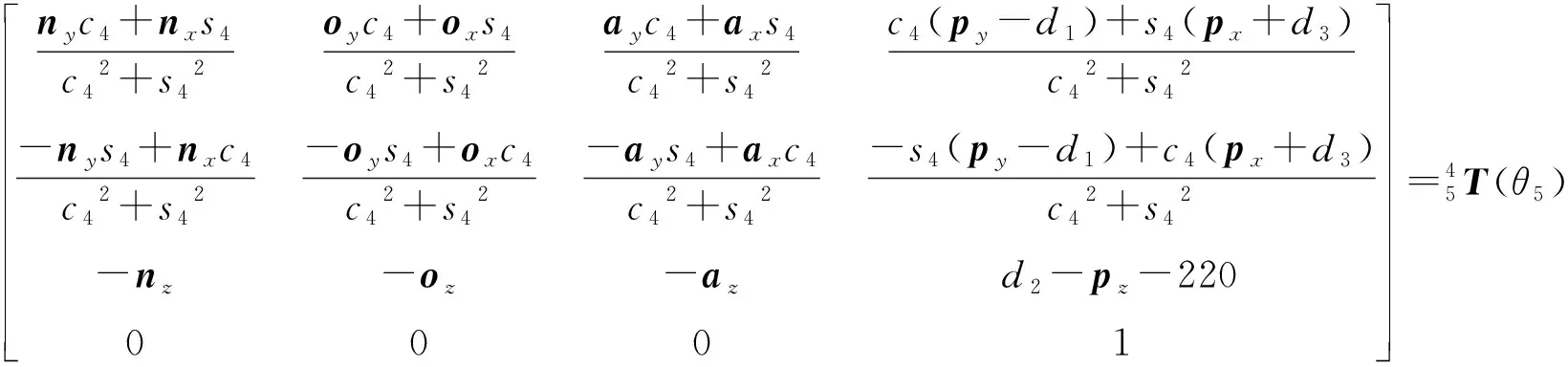
(8)
令矩阵方程(8)两端的元素(2,3)对应相等,可得axc4-ays4=0,从而可求出
(9)
由式(5)得:
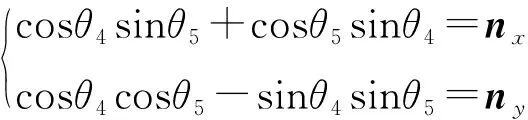
(10)
从而可求出
(11)
3 驱动机器人的工作空间分析及仿真验证
工作空间指的是末端执行机构上参考点在空间中可以达到的所有点的集合[7],本文驱动机器人的参考点定为磁球的质心。分析驱动机器人的工作空间可以避免逆运动学计算过程中机器人末端运动轨迹不在最大工作空间内,从而确保逆解的存在。
3.1 建立运动学仿真模型
利用MATLAB软件高效的数值计算、数据分析、数据可视化等特点,运用机器人工具箱(robotics toolbox)建立驱动机器人的仿真模型,并编写相应的简单算法,不但可以完成驱动机器人的运动学仿真,还能验证其正、逆解运动学的正确性。因此,根据D-H参数的范围,利用MATLAB工具箱中的link等函数输入以下代码并运行,便可建立驱动机器人的运动学模型,如图4所示。
L0=Link(′theta′,pi,′a′,0,′alpha′,pi/2);
L1=Link(′ theta′,0,′a′,0,′alpha′,-pi/2);
L2=Link(′ theta′,pi/2,′a′,0,′alpha′,pi/2);
L3=Link(′ theta′,0,′a′,0,′alpha′,-pi/2);
L4=Link(′d′,-150,′a′,0,′alpha′,-pi/2);
L5=Link(′d′,0,′a′,70,′alpha′,0);
bot=SerialLink([L0,L1 L2 L3 L4 L5],′name′,′Magnetic Drive Robot′)
teach (Robot)

图4 运动学仿真模型
图4显示的位置姿态信息与图3相同,因此验证了驱动机器人的运动学仿真模型的正确性。
3.2 工作空间的计算求解
本文机器人末端工作空间的求解采用蒙特卡洛法(Monte Carlo method)[8],该方法是一种通过随机概率来解决问题的数值方法,可以实现运动空间的可视化,能够快速计算得到可行点,适用于多关节型机械手臂的工作空间求解。
驱动机器人的工作空间求解方法如下:
1) 根据驱动机器人的结构参数大概算出其工作空间范围。
2)通过MATLAB软件中的Rand函数,随机产生大量0~1间的数值,将这些随机数值定为随机步长变量,从而得到各关节的伪随机值θi:
θi=θimin+(θimax-θimin)×Rand(N,1)
(12)
式中:θimin为关节变量的最小值;θimax为关节变量的最大值;N为 0,1 之间随机数值的个数;i为关节变量的数目。
3)将2)产生的随机值代入驱动机器人的正运动学方程,计算出驱动机器人末端的位置。求出的末端坐标点数目越多,得到的驱动机器人实际工作空间就越精确。
4)利用MATLAB软件画出驱动机器人的工作空间,便能获得驱动机器人末端的工作空间点云图,也就是蒙特卡洛工作空间。
运用蒙特卡洛法在MATLAB软件上进行简单编程,计算得出驱动机器人的工作空间。设置随机坐标点的数量为N=15 000,得到驱动机器人的工作空间如图5所示。
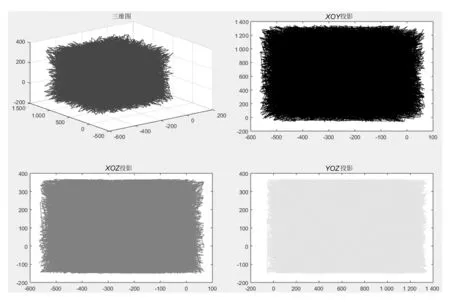
图5 驱动机器人的工作空间
从图5可以得到驱动机器人的工作空间为:x∈[-548,50]mm,y∈[0,1 280] mm,z∈[-150,368] mm,驱动机器人的工作空间接近于一个长方体。MATLAB软件模拟出的工作空间与各个关节的真实工作空间相符,空间尺寸与驱动机器人结构设计的尺寸一致,从三维图及各方向投影图上可以看出,坐标点分布均匀并且无明显空洞,工作空间非常紧凑,因此验证了蒙特卡洛法求解驱动机器人工作空间的正确性。
4 结束语
本文建立了胶囊内窥镜驱动机器人的三维模型,对驱动机器人进行了正、逆运动学求解,获得驱动机器人的运动学方程和执行末端位姿矩阵,通过MATLAB仿真验证了驱动机器人运动学模型的正确性;蒙特卡洛法计算得到的驱动机器人工作空间与各个关节的真实工作空间相符,空间尺寸与驱动机器人结构设计的尺寸一致。本文的分析为后续的动力学、多物理场仿真分析、联合控制仿真奠定了理论基础,也为类似的驱动机器人动力学仿真分析提供了有益的借鉴。

