基于路径灵活性的两阶段开放式低碳选址-路径问题

刘成清，胡大伟，黄 榕

(长安大学汽车学院，西安710064)

随着经济发展与城镇化进程的加快，城市人口与汽车保有量快速增长，导致城市物流配送需求快速上升，交通拥堵问题日益严重。城市交通拥堵导致运输车辆配送效率降低，CO2排放增加，这与巨大的城市物流配送需求及节能减排的物流产业发展理念相矛盾。在短时间内，城市交通拥堵问题无法彻底解决，因此，节能、环保、高效的城市配送规划方案成为缓解当前矛盾的有效措施。近年来，如何减少运输过程中的CO2排放和燃油消耗成为众多学者研究的热点。Bektas等[1]在传统车辆路径问题中考虑CO2排放，基于综合排放模型，提出了燃油车的污染-路径问题(polluted routing problem,PRP)，并针对该问题的特点，建立准确的模型；Demir等[2]基于总成本与时间的背反原理，构建双目标的PRP模型，并提出了算法解决100个节点内的PRP问题；Koc等[3]以最小化排放为目标，建立异质车队的选址-路径问题模型，并提出一种自适应大邻域搜索的元启发式算法求解该问题。Ehmke等[4]考虑不同时段路网的交通情况，提出基于时间的最小化燃油消耗的车辆路径问题，以决策在城市配送区域进行配送活动时的车辆路径和出发时间。考虑城市交通存在路径可替代性强、拥堵空间分布不均等特点，Huang等[5]基于PRP问题，明确提出“路径灵活性”概念，建立确定和随机交通情形下，基于路径灵活性和时间依赖性的车辆路径问题模型，并以北京为例，测试模型和算法的有效性和实用性。Fabian等[6]在经典车辆路径问题(vehicle routing problem,VRP)中考虑路径灵活性，分别以最小化总成本、燃油消耗/排放量、距离和旅行时间为目标建立模型，并对比分析其差异。大量研究表明，在运输配送规划中，考虑城市路网的路径灵活性有助于减少能量消耗及CO2排放。

与PRP问题相比，选址-路径问题(location routing problem,LRP)的研究起步较早，目前已取得丰富的成果，但仍存在许多有待发掘的领域[7-11]。胡大伟[12]运用系统分析的思想和方法研究了物流系统中的LRP问题，并提出了多种启发式算法，对LRP数学模型进行优化求解；Contardo等[13]建立了带容量限制的两阶段选址-路径问题(2E-LRP)模型，并提出一种分支切割精确算法和自适应大邻域搜索元启发式算法；Vidovic等[14]建立了非危险、可回收物品的2E-LRP数学模型，并提出一种两阶段贪婪启发式算法；Pichka等[15]基于2E-LRP问题，分析城市中开放式路径的可能性，提出两阶段开放式选址-路径问题(2E-OLRP)，针对该问题建立了3种数学模型，并提出一种改进的模拟退火算法。

研究发现，针对LRP或2E-LRP问题的相关研究中，未考虑实际路网情况，且仅根据距离计算运输成本，与实际运输过程存在较大差异；大部分PRP问题和考虑路径灵活性问题的研究都仅针对单一路径问题，而将选址与路径问题进行整体研究，比考虑其单一因素更能节约总成本，且2E-LRP模型有利于优化整体运输配送网络，进一步降低总成本。此外，城市配送网络中客户点多、分布广，且城市路网存在路径可替代性强、交通拥堵空间分布不均等特点。因此，基于2E-OLRP模型，在总成本中考虑燃油消耗和CO2排放成本，在路径规划中考虑路径灵活性，构建2E-OLCLRP-WF模型，研究路径灵活性对总成本和CO2排放的影响，为物流企业规划节能、环保、高效的城市物流配送方案提供理论支撑和决策参考。

1 模型建立

1.1 问题描述

假设有一个仓库V0，Ns个配送中心，Nc个客户点，Nm个交叉口。所有的客户点都必须被服务，且只能被访问一次；交叉口可被多次访问，也可不被访问；每辆车的装载量不超过最大车容量；任意配送中心服务的客户总需求不超过该配送中心的最大容量；客户点只能由配送中心服务；最后，以最小化总成本为目标，在第一阶段中，确定分配给每个配送中心的客户以及第一层车辆的路径，在第二阶段中，确定第二层车辆的路径。

图1所示为2E-OLCLRP-WF模式的示意图。第一层的车辆从仓库出发，服务配送中心后，终止于该路径上的最后一个配送中心，第一层车辆的路径由实线箭头表示，其中，第一层的车辆只能经过仓库、配送中心和交叉口，不能经过客户点；第二层的车辆从配送中心出发，服务客户后，终止于该路径上的最后一个客户，第二层车辆的路径由虚线箭头表示，其中，第二层的车辆只能经过配送中心、客户点和交叉口，不能经过仓库。两点之间能否直接到达取决于实际的路网情况。

路径灵活性示意图如图2所示。图中1和2分别表示两个客户点，从客户点1到客户点2存在3条不同的路径。路径灵活性是指两点之间存在多条可供选择的路径，根据不同的车辆装载量及各弧上的速度选择的最优路径可能存在较大差异，因此，3条路径均可能是客户点1到客户点2的最优路径。

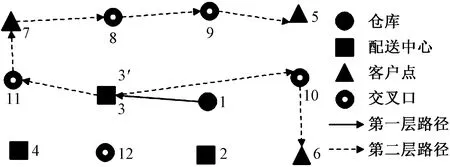
图1 2E-OLCLRP-WF问题示意图Fig.1 The sketch of 2E-OLCLRP-WF problem

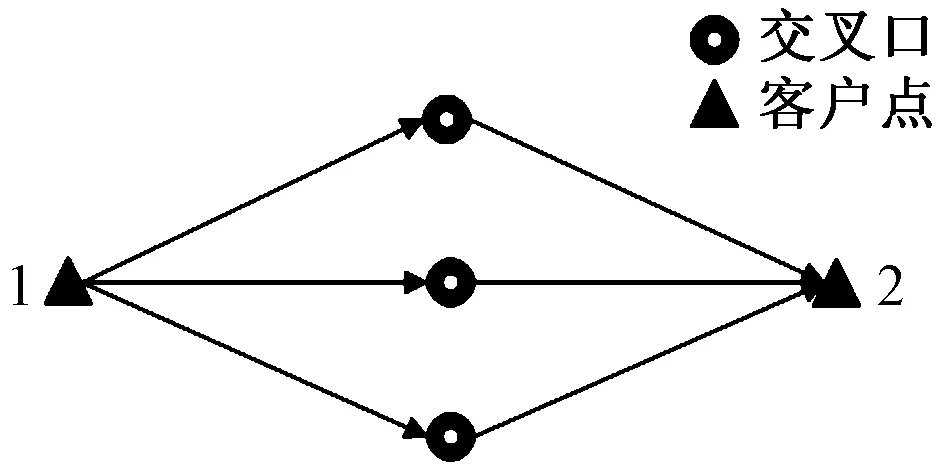
图2 路径灵活性示意图Fig.2 The sketch of path flexibility

1.2 参数定义与模型假设

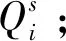
假设1：在1 d的时间段内进行配送规划。

假设2：仓库、配送中心处的车辆数无限制。

1.3 运输成本计算

2E-OLCLRP-WF问题中运输成本由燃油消耗成本和CO2排放成本组成，根据Barth等[16]、Scora等[17]所提出的综合排放模型，燃油消耗率可由式(1)计算。

FR=ξ(sNV+P/η)/κ

(1)

式(1)中：ξ为空燃比；s为发动机的摩擦系数，kJ/(rad·L)；N为发动机转速，rad/s；V为发动机排量，L；η和κ为常数；P为发动机输出的功率，kW，可由式(2)计算。

P=Ptract/ηtf

(2)

式(2)中：ηtf为车辆传动系统的传动效率；Ptract为作用在车轮上的总驱动力，N。

Ptract=(Mτ+Mgsinθ+0.5CdρAv2+MgCrcosθ)v/1 000

(3)

式(3)中：M为车辆的总质量，kg；M=w+f，w为车辆整备质量，kg；f为车辆负载，kg；v为车速，m/s；τ为加速度，m/s2；θ为道路坡度，(°)；g为重力常数，m/s2；Cd为空气阻力系数；Cr为滚动阻力系数；ρ为空气密度，kg/m3；A为车辆迎风面积，m2。

令弧(i,j)的长度为d，车辆在该弧上的速度为v，λ=ξ/κφ，γ=(1/1 000)ηtfη。其中，φ为燃油消耗率单位转换系数；α=τ+gsinθ+gCrcosθ为车辆-路径的固定常数；β=0.5CdρA为车辆的固定常数。则弧(i,j)上，车辆的燃油消耗量可表示为车速v和负载f的函数，如式(4)所示。

F(v,M)=λ(sNV+wγαv+γαfv+βγv3)d/v

(4)

车辆的运输成本与燃油消耗量成正比，比例系数为单位燃油与CO2排放量的成本。

1.4 CO2排放量计算

根据联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)碳排放计算指南[18]推荐的燃油碳排放因子及参数值，采用式(5)计算每升柴油、汽油的CO2排放量V(CO2)，kg/L。

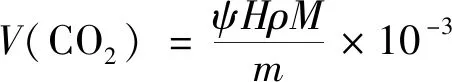
(5)

式(5)中：ψ为柴油/汽油的碳排放因子，由IPCC指南查得分别为20.2 kg/GJ、18.9 kg/GJ；H为柴油/汽油的热值，kJ/g；ρ为柴油/汽油的密度，g/mL；M为CO2的摩尔质量，取44；m为CO2中碳元素的摩尔质量，取12。

经计算，每升柴油、汽油的CO2排放量分别为2.74 kg/L、2.47 kg/L。

1.5 建立模型

建立2E-OLCLRP-WF模型如下：

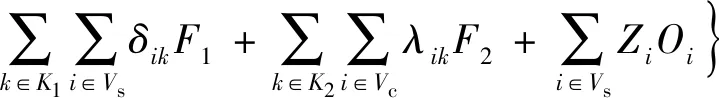
(6)

式(6)表示最小化第一层和第二层的运输成本、第一层和第二层车辆固定成本以及配送中心开放成本之和。

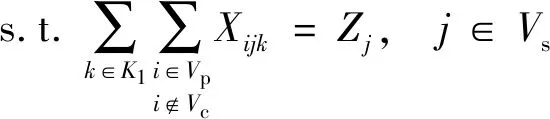
(7)

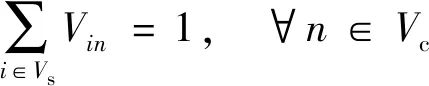
(8)

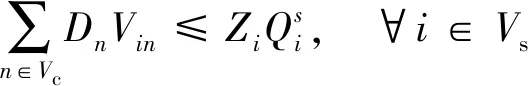
(9)

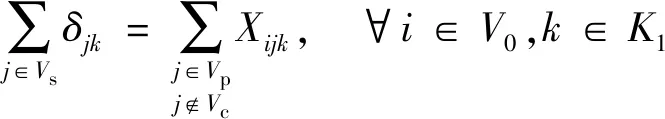
(10)

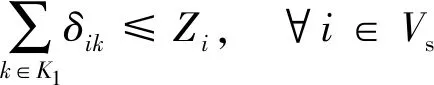
(11)

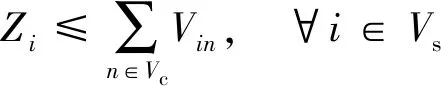
(12)

Uijk≤Q1Xijk, ∀i∈Vp,j∈Vp,k∈K1,i≠j

(13)

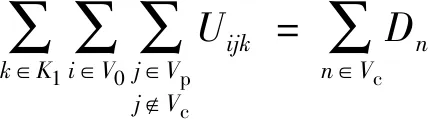
(14)

(15)

(16)

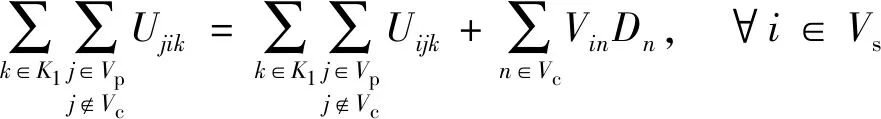
(17)

(18)

Xijk≤Rij, ∀i,j∈Vp,k∈K1

(19)

约束(7)～约束(19)与第一阶段相关。约束(7)表示开放的配送中心由一辆第一层的车辆服务，未开放的配送中心无车辆服务。约束(8)表示每个客户均只由一个配送中心服务。约束(9)表示分配给开放的配送中心的客户总需求不超过该配送中心的最大容量。约束(10)表示从仓库出发的第一层车辆全部终止于配送中心，而不回到仓库。约束(11)表示开放的配送中心至多是一辆第一层车辆的终点配送中心，未开放的配送中心不能作为终点配送中心。约束(12)表示开放的配送中心至少服务一个客户点。约束(13)为第一层的车容量约束。约束(14)表示从仓库运出的总货物量等于客户的总需求。约束(15)和约束(16)为第一层的车流量平衡约束。约束(17)和约束(18)为第一层的货流量平衡约束。约束(19)表示两点间存在直达道路，车辆才能直接到达；若不存在直达道路，则需要经过交叉口。

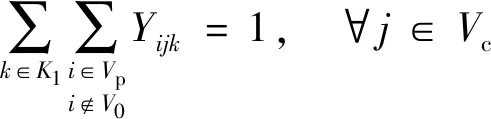
(20)

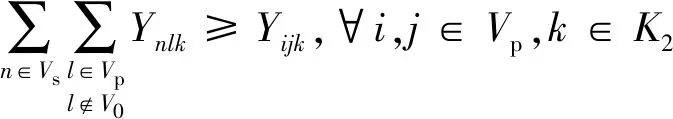
(21)

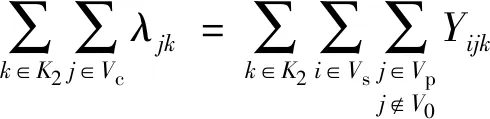
(22)

(23)

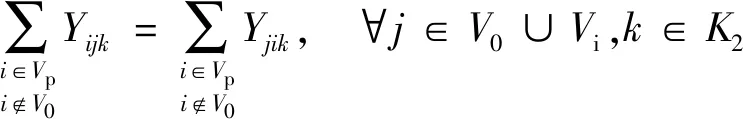
(24)

Lijk≤Q2Yijk, ∀i,j∈Vp,i≠j,k∈K2

(25)

(26)

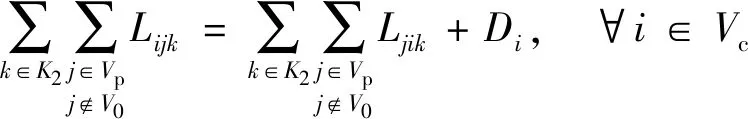
(27)

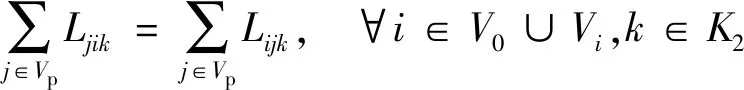
(28)

Yijk≤Rij, ∀i,j∈Vp,k∈K2

(29)

约束(20)～约束(29)与第二阶段相关。约束(20)表示每个客户点有且仅有一辆第二层的车辆到达。约束(21)表示第二层车辆的起点必须是配送中心。约束(22)表示被使用的第二层的车辆全部终止于客户点。约束(23)和(24)为第二层的车流量平衡约束。约束(25)为第二层的车容量约束。约束(26)表示从某一配送中心配送的货物总量等于该配送中心服务的客户的总需求量。约束(27)和(28)是第二层的货流量平衡约束。约束(29)表示两点间存在直达道路，车辆才能直接到达；若不存在直达道路，则需要经过交叉口。

vmax≤vij≤vmin, ∀i,j∈Vp

(30)

约束(30)表示两层车辆的速度均不超过最高速度，且不低于最低速度。

为进行对比，以验证2E-OLCLRP-WF模型的优越性，在文献[15]中，2E-OLRP模型的总成本中考虑燃油消耗和CO2排放成本，建立2E-OLCLRP模型，其总成本(目标)函数见式(31)。式(31)表示最小化第一层、第二层的运输成本和车辆固定成本，以及配送中心开放成本之和。该模型的约束与文献[15]中约束相同。

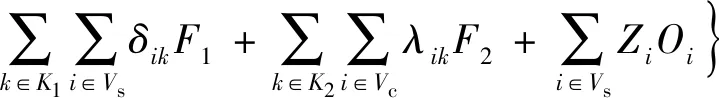
(31)

2 案例计算

采用某市部分路网作为案例，该路网及仓库、配送中心、客户点和交叉口位置如图3所示。其中包括：一个仓库(1)、3个配送中心(2～4)、6个客户点(5～10)和29个交叉口(11～39)，各点的相关参数如表1所示。通过谷歌地图获得各点间距离及速度，其中速度为一天时间段内的平均速度。

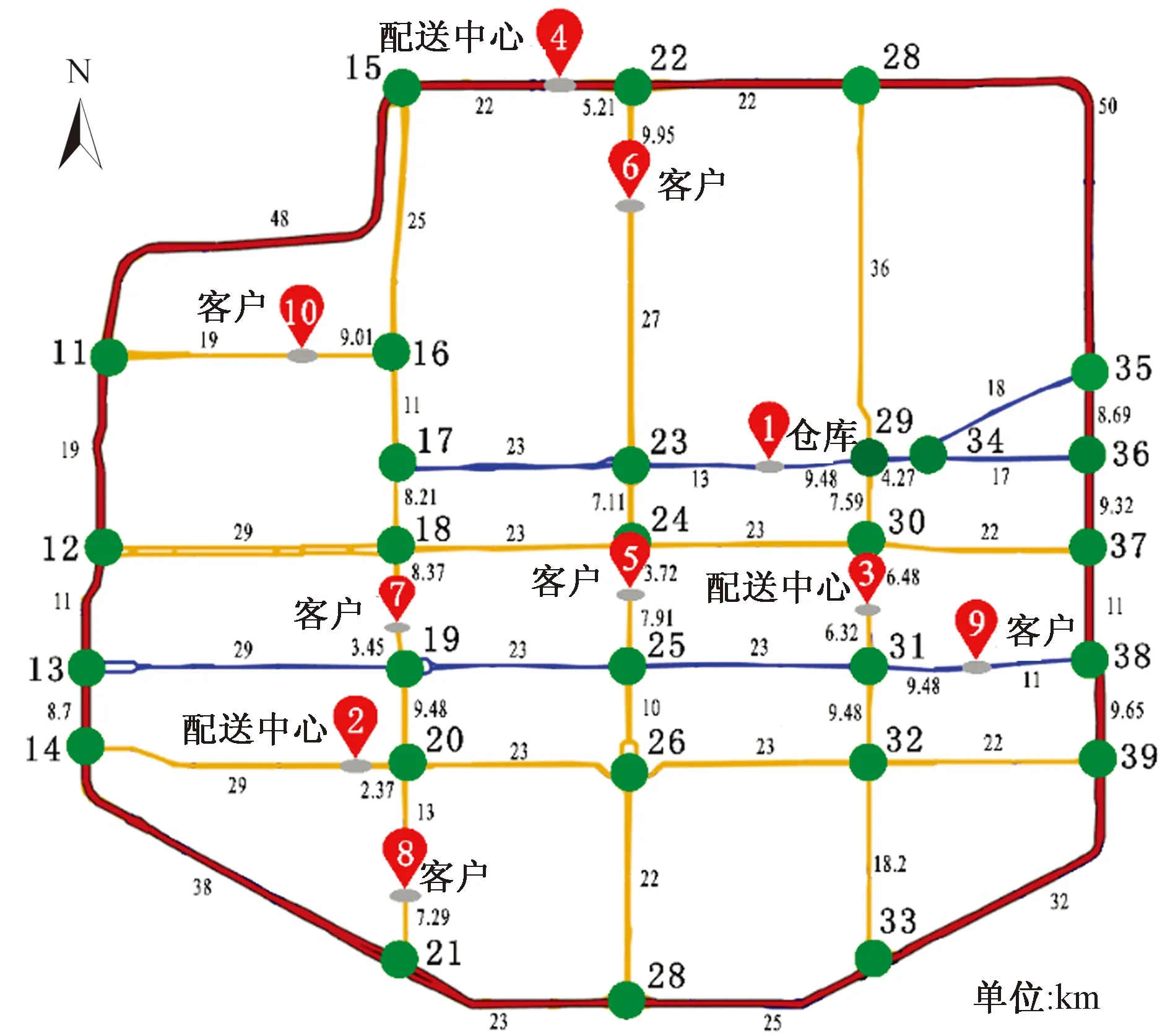
图3 城市交通网络图Fig.3 The city traffic network in case

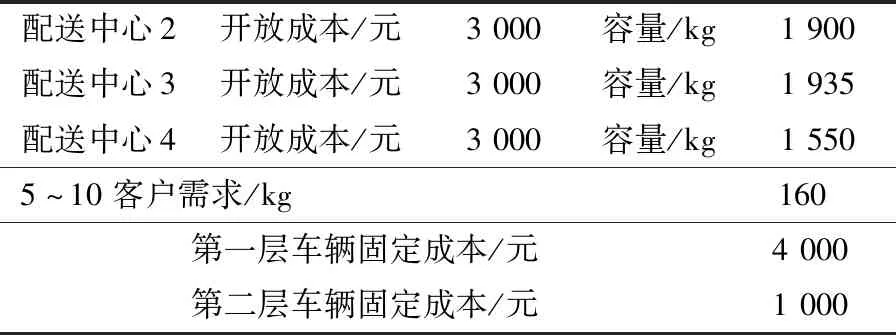
表1 实例参数Table 1 The case parameters

与燃油消耗和CO2排放相关的车辆参数取值如表2所示。参考城市实际物流配送车型，第一层车辆选用柴油车，第二层车辆选用汽油车。

为得到2E-OLCLRP模型中仓库、配送中心和客户各点间的最短路径及其距离，根据表1数据与图3，利用Dijkstra算法编程求解，所得最短路径(距离)如表3所示。

表3中第一行(列)表示仓库(1)、配送中心(2～4)和客户点(5～10)。例如：第二行、第三列表示点1到点2的最短路径为：1-23-24-5-25-19-20-2，括号内的数值表示最短距离为66 600 m。仓库、配送中心、客户点各点间的速度为两点间最短路径上的平均速度。

3 结果分析

将2E-OLCLRP-WF模型利用精确求解器CPLEX对算例进行求解，得到总成本为9 298.25元，其中运输成本298.25元；编程求得CO2排放量为63.04 kg。求解信息如表4和图4所示。最优路径如图5所示，第一层的车辆路径由实线箭头表示，由一辆第一层的车辆完成运输任务；第二层的车辆路径由虚线箭头表示，其运输任务由两辆第二层的车辆完成。

为求解2E-OLCLRP模型，将本文案例当作1个仓库、3个配送中心和6个客户点的配送网络。根据表3中各点间的最短路径，利用燃油消耗函数式(4)计算各点间的运输成本(燃油消耗量×单位燃油及其CO2排放成本)，并以式(31)为目标函数求解2E-OLRP模型，所得2E-OLCLRP问题模型的最优路径如图6所示。图6配送方案的总成本为9 316.81元，其中运输成本为316.81元，CO2排放量为67.05 kg。

求解结果表明，与2E-OLCLRP问题模型相比，2E-OLCLRP-WF模型总成本节约0.20%，其中，节约运输成本5.86%，减少CO2排放5.98%。证明了本文所提出的模型在节能减排方面的优越性。

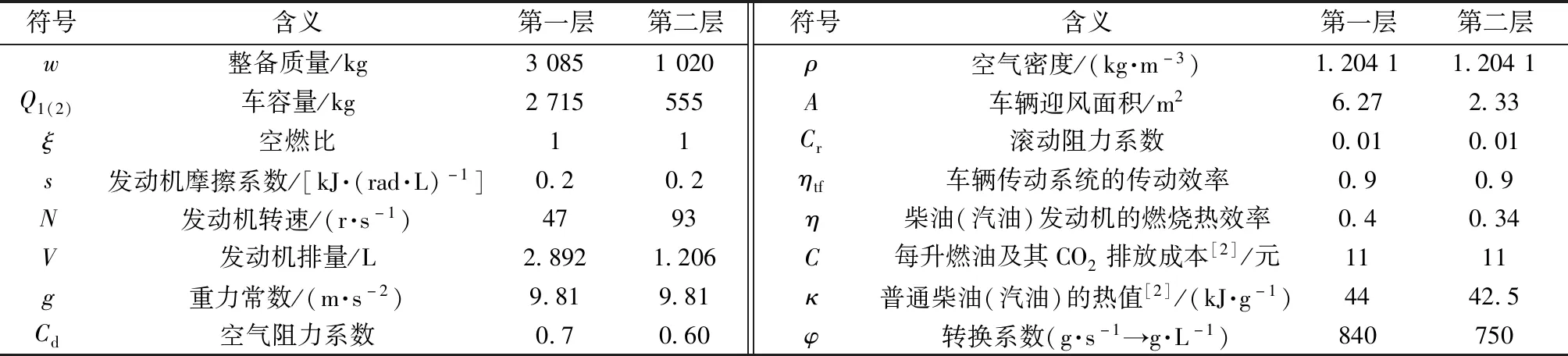
表2 车辆相关参数Table 2 Parameters and values relating to vehicle

表3 最短路径(距离)Table 3 The shortest path (distance)

表4 CPLEX求解信息Table 4 The solving information of CPLEX

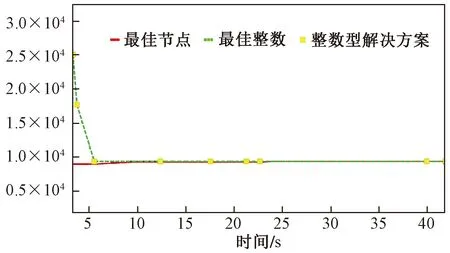
图4 CPLEX求解时间Fig.4 The solving time of CPLEX

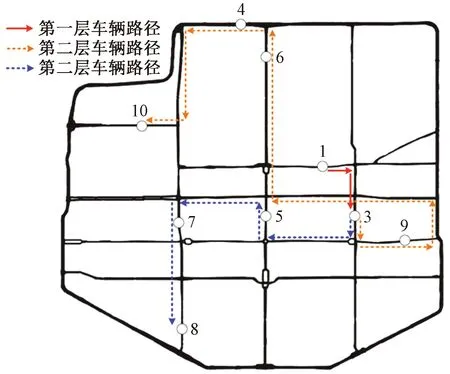
图5 2E-OLCLRP-WF模型的最优路径Fig.5 Optimal paths of 2E-OLCLRP-WF model

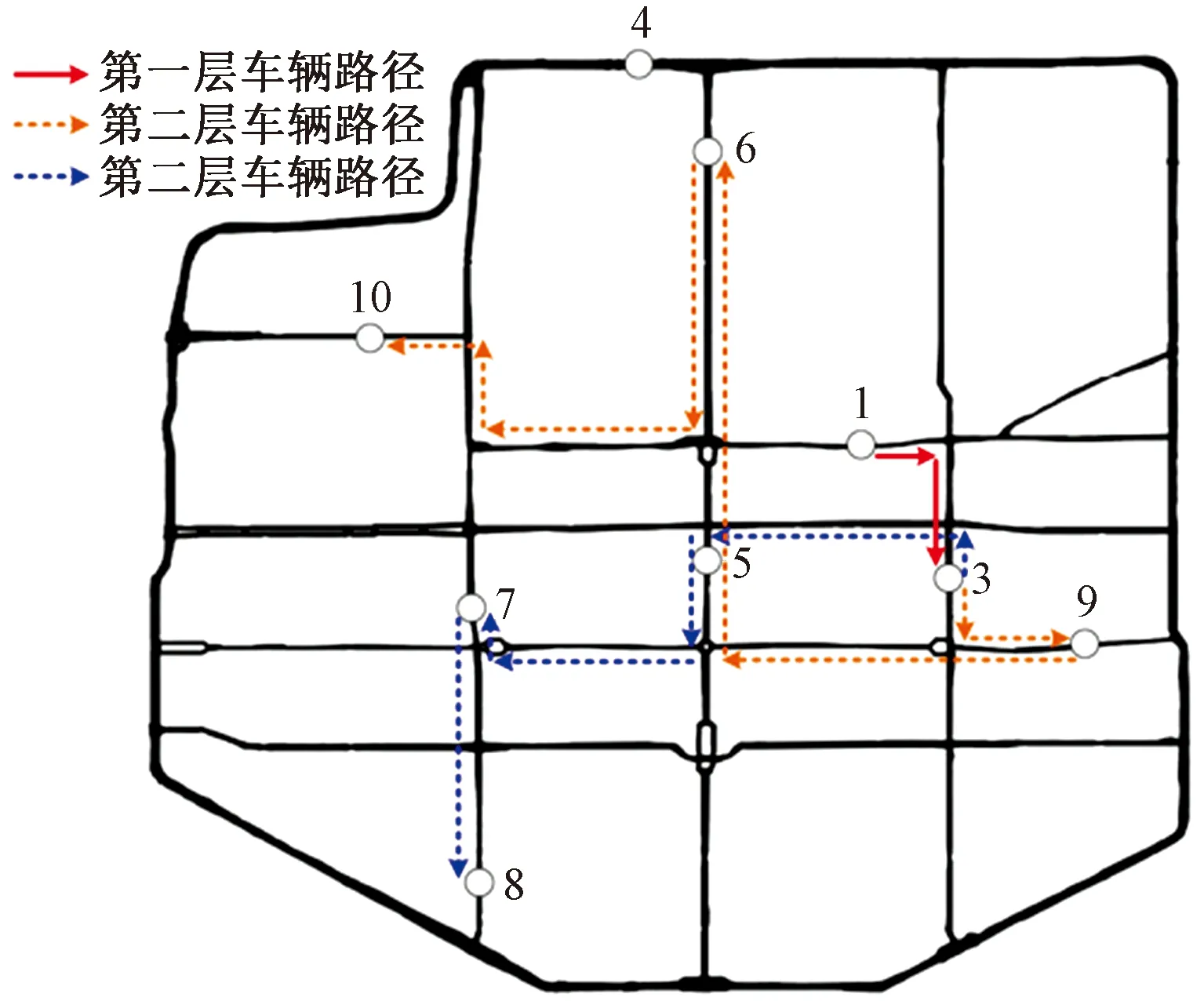
图6 2E-OLCLRP模型最优路径Fig.6 Optimal paths of 2E-OLCLRP model

由图6可知，与图5中的最优路径相比，图6中第二层车辆的路径发生了较大变化，但选择开放的配送中心未发生变化，这主要是由于本文案例中客户点的规模较小，而配送中心的开放成本较大，各点间路径的灵活选择所导致的总成本的变化较小，不足以影响开放配送中心的决策。

4 结论

针对城市配送客户多、范围广、路径可替代性强等特点，考虑路径灵活性，同时考虑燃油消耗和CO2排放成本，建立以最小化总成本为目标的城市网络配送模型。为验证模型的优越性，基于城市路网图，利用精确求解器CPLEX对所建立的2E-OLCLRP-WF模型和2E-OLCLRP模型进行求解，并将两种模型的最优路径进行对比分析。结果表明：①城市交通网络运输配送的路径决策具有较高的灵活性；②与2E-OLCLRP模型相比，2E-OLCLRP-WF模型能节约运输成本并减少CO2排放；③在小规模数据下，考虑路径灵活性对总成本影响较小，但在节能减排方面仍具有较大的优越性。研究结果可为城市网络中物流配送的路径规划提供理论支持。

未来的研究可以从以下几个方面入手：①开发启发式算法求解大规模的2E-OLCLRP-WF问题；②考虑更接近实际配送情形的因素，如时间窗约束等；③考虑顾客需求不确定性等因素。