基于数据挖掘的水库最优分水比计算方法研究

刘鑫, 韩宇平

(华北水利水电大学 水利学院,河南 郑州 450046)

我国水资源优化配置方面的研究最初是以水库优化调度为先导。20世纪80年代初,以华士乾教授为首的项目组对北京地区的水资源系统进行了研究,该项研究成为水资源系统中水量合理分配的雏形[1]。流域水资源规划涉及到中央、地方多个决策层次,部门、地区多个决策主体,属于群决策问题;涉及到近期、远期多个决策时段,是多时段决策问题;具有社会、经济和生态环境等方面的多个决策目标,是典型的多目标决策问题[2]。在水资源的合理配置中,要解决水资源供需矛盾与各类用水竞争等一系列复杂关系,就要找到最合理的配置方案,该方案可能不能让每个用水单元的效益都达到最好,但对整个水资源分配体系来说,其总体效益是最好的。

目前，有关水资源配置方面的研究成果有很多。如钟鸣等[3]将改进的粒子群优化算法运用到水资源配置中。郭旭宁等[4]建立了基于0-1规划方法的水库群最优化调度模型。吴云等[5]提出了一种改进多目标猫群算法求解模型。彭少明等[6]建立了泛流域多维尺度优化模型,采用大系统协调技术和嵌套遗传算法动态调节机制对模型进行求解。陈晨等[7]提出了基于综合集成平台的水资源动态配置新模式。李丽琴等[8]以可持续发展为依据进行水资源配置的评价。游进军等[9-11]采用基于规则的全模拟技术建立了水资源系统分析模型。

但是,关于水库最优分水比计算的研究还不够深入。随着用水单元的增多,分水比的计算时间呈几何增长。而在基于规则的水资源合理配置模型计算中,水库分水比问题直接影响到水资源合理配置方案的形成。在水资源量一定的前提下,要找到最合理的配置方案,计算水库的最优分水比是重要的途径。在大数据时代,先进的大数据技术具有自动预测以及趋势分析的重要功能。通过挖掘数据隐藏的规律,融合大数据技术,能够从根本上突破传统的“定性—定量—再定性”的统计分析过程,打破复杂规则下海量数据无法计算的僵局,将分析过程简化为“定量—定性”,发现规律可以不受任何假设的限制,分析思路可以概括为“发现—总结”。这样就能够全方位解决高精度分水比的计算问题,给水资源合理配置补短板提供了技术保障。

基于上述思想,本文在基于规则和一定空间复杂度的情况下,分析了不同步长最优分水比的计算时间,从海量数据中通过算法挖掘数据隐藏的规律,提出了分布式算法且进行了有效分析,并最终计算出步长为0.001的最优分水比。

1 研究区资料与水资源合理配置的规则

1.1 研究区资料

研究区位于湖北省中部,区域内包括漳河水库流域和灌区两部分。其中漳河水库流域是指漳河水库坝址以上的汇水区域,面积为2 212 km2,平均高程400 m左右。漳河水库灌区面积5 543.93 km2。漳河流域的水资源分布情况如图1所示。

图1 湖北省漳河流域水资源分布图

本文主要研究的是漳河水库最优分水比的计算问题,因此选取漳河水库灌区的6个用水单元为代表,分别是东宝区、掇刀区、沙洋县、钟祥市、荆州区和当阳市,以过去43 a逐年逐月的统计数据计算漳河水库43 a的总缺水量最小且兼顾时间效益的最优分水比。数据主要来源于荆门市统计年鉴和其他县市的统计年鉴、水资源管理委员会办公室调查统计的社会经济和土地利用资料以及各地的农业统计年报等；水库用水量采用水库水量平衡计算的数据；降雨蒸发资料来源于研究区8个水文站和气象站及18个雨量站,对于个别缺测的月份,通过建立缺测站与参证站同步系列相关曲线来插补缺测站的资料。表1为研究区大中型水库的特征参数。

表1 大中型水库的特征参数

1.2 水资源合理配置的规则

现实中大型水库对各地区的供水已经有一定的约定或者分水协议,供水调度必须遵守。否则,单纯地从优化目标进行供水优化分配可能会导致地区之间的用水矛盾。因此,对于这样的水库,当进行供水调度计算时,水库对下游单元的供水量应按确定的分水比进行分配,计算公式如下[12]:

(1)

式中:αi为水库给第i下游单元供水的分水比；Qi为水库对第i下游单元的供水量，万m3;Qtotal为水库的可供水总量,万m3。

在湖北漳河水库灌区供水体系中,漳河水库是最重要的一个供水源。在供需平衡计算中,塘堰、小型水库首先进行供水,在上述水源供水不足的情况下再由中型水库按照既定的供水比例供水,然后是河坝引水、泵站提水,最后由漳河水库对各单元进行供水。漳河水库给各用水单元的分水比例会在很大程度上影响到所有供水区的水资源满足程度和总缺水量情况。

水资源合理配置的规则如下:①供水顺序为塘堰、小型水库、中型水库、河坝引水、泵站提水及漳河水库。②从数据库中读取城镇生活、农村生活、二三产业和农业的需水量及退水系数,读取大中型水库的入流系列及水库特征参数、调度规则、调度线、各用水单元的当地径流系列、各用水单元的降雨量及水面蒸发系列、各类工程渠系水利用系数与漳河水库的分水比；然后嵌套循环,逐年逐月逐用水单元按照水资源合理配置的规则,计算城镇生活、农村生活、二三产业、农业及河道内生态的供水量与缺水量、水库的时段库容与蒸发量,及6个用水单元与各单元各需水类别的年缺水量、总缺水量等。水资源合理配置规则的流程图如图2所示。

图2 水资源合理配置规则的流程图

水库的供水关系如图3所示。

图3 研究区大中型水库的供水关系

2 问题描述

研究区内包含6个用水单元,为了求得漳河水库对各用水单元的最优分水比,首先设置初始步长,得到每个单元的有效取值集合,利用公式(1)计算得到满足条件的分水比候选集合,最后根据规则计算候选集合中的每一组分水比,找出最优的那组。

如果设定步长为0.001,那么根据公式(1),可以得到每个单元分水比的取值集合为{0.001,0.002,…,0.995},集合内共有995个值。计算候选集合时,需要循环遍历6个用水单元的取值集合,找到满足公式(1)的分水比加入到候选集合中,遍历结束就可以得到分水比候选集合。在没有先验经验的地区,计算候选集合需要进行9956次运算。在计算最优分水比时,一般考虑选取缺水量最大的年份或几个典型年份进行计算。由于不同年的数据差别较大,计算出某些年份缺水量为零的分水比组合较多,而这些分水比组合用于计算其他年份的缺水量时会出现翻倍的情况且波动较大。此外,43 a的年均缺水量数值差别不明显,不利于寻找规律。因此,本文求43 a总缺水量最小时的分水比。根据研究区的配水规则,使用配置了酷睿i7 CPU的计算机计算一组分水比下43 a供水的总缺水量耗时约1.6 s。因此,步长设置为0.001时,最优分水比计算时间趋于无穷大。不同步长的取值集合、取值个数、求解候选集合运算次数和最优分水比计算时间详见表2。

表2 不同步长的取值集合、取值个数、求解候选集合运算次数和最优分水比计算时间

通过分别计算发现,步长为0.03、0.06、0.07及0.09的候选集合取值个数较少,总缺水量的计算结果都较大。另外,0.08是0.04的倍数,0.04的取值集合已经包含了0.08的取值集合。因此,这些步长不予考虑。由表2中数据可见,当步长逐渐缩短时,求解候选集合的运算次数呈几何增长,从而导致计算时间大幅度增加,求解步长0.01的候选集合已经很难实现,导致无法计算最优分水比。本文利用数据挖掘的方法,从“定量的回应”中搜索隐藏于其中有价值的信息,提出了分布式算法,并最终计算出步长为0.001的分水比。

3 分布式算法的提出与计算分析

3.1 分布式算法

由公式(1)可知,各分水比之和等于1,意味着一个单元分水比的增大通常以减小另一个单元的分水比为代价。对于任何一个研究区,总有一个分水比的大小关系存在。对于本文的研究区,通过研究发现,6个用水单元中沙洋县和荆州区的分水比越大,或东宝区和掇刀区分水比越小,则总缺水量越小。由此,本文采用一种固定的算法求分水比的候选集合,然后再计算最优分水比。当运算到一定程度时,不同步长计算结果的变化曲线在水平方向的趋势呈现周期性变化,竖直方向有一定程度的拉伸。计算流程如下:

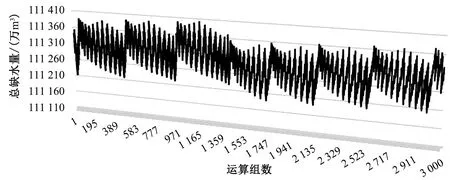
输入漳河水库6个用水单元(东宝区、掇刀区、钟祥市、当阳市、沙洋县、荆州区)的分水比初始集合，分别为S1、S2、S3、S4、S5、S6。将集合中的元素按从小到大排序,则有S1=S2=S3=S4=S5=S6={s1,s2,…,sn},s1

设置6层递归关系,S1作为最外层,S6作为最内层。计算候选集合的时候,S1优先取值,且取值满足从集合内最小值开始递增,S2优先级次之,取值也是从集合内最小值开始递增,但是取值速率要大于S1。内层的S6优先级最低,取值满足从集合内最大值开始递减(因为前5个集合都是从最小值开始取)。S5虽然是从集合内最小值开始取值,但是由于S5处于次内层,所以取值递增的速率快,这样就满足了上述先验经验。

步骤1:鉴于各分水比集合均采用队列结构存储,判断S1是否为空,如果为空,即得到最终候选集合C;否则,从S1中抽取集合的第1个值,即最小值,跳转至步骤2。

步骤2:判断S2是否为空,如果不空,从S2中抽取集合的第1个值,即最小值,跳转至步骤3;否则,跳转至步骤1。

步骤3:判断S3是否为空,如果不空,从S3中抽取集合的第1个值,即最小值,跳转至步骤4;否则,跳转至步骤2。

步骤4:判断S4是否为空,如果不空,从S4中抽取集合的第1个值,即最小值,跳转至步骤5;否则,跳转至步骤3。

步骤5:判断S5是否为空,如果不空,从S5中抽取集合的第1个值,即最小值,跳转至步骤6;否则,跳转至步骤4。

步骤6:判断S6是否为空,如果不空,从S6中抽取集合的第1个值,即最小值,跳转至步骤7;否则,跳转至步骤5。

步骤7:对于取满6个值的一组数Ci=(c1,c2,c3,c4,c5,c6),如果c1+c2+c3+c4+c5+c6=1,则将Ci添加到最终候选集合C中;否则丢弃。跳转至步骤6。

选取步长0.04,采用上述算法计算分水比候选集合,然后再计算最优分水比。从中取5 000组运算数据进行展示,图4即为步长为0.04时总缺水量的运算趋势图。

图4 步长为0.04时总缺水量的变化趋势(5 000组运算数据)

由图4可以发现,在一定的范围内,随着运算组数的增加,总缺水量呈现周期性递减趋势。在达到一定运算组数时,总缺水量立即回弹至极大值后,继续在一定范围内周期性变化。此外,不同周期内的最小值差在50万m3以内,且趋于一个极小值。由此推测,不同步长的分水比计算过程中,也会呈现出此种周期性变化的规律。鉴于此,选取步长0.02、0.04、0.05分别进行计算,为了更加清晰地显示数据的变化趋势,从步长0.04和0.05的运算数据中取2 700组运算数据进行展示,从步长0.02的运算数据中则取6 000组数据进行展示,如图5所示。

图5 3种步长时总缺水量的变化趋势

由图5可以发现,3种步长对应的总缺水量变化周期(P)的关系为:P0.05Q0.04>Q0.02。综上,3种不同步长的总缺水量呈现相似的变化趋势,且随着步长的减小,对应的变化周期变长,但该步长对应周期内总缺水量的最小值更小,步长0.02在不同周期内最小值的差在20万m3以内。证明前面的推测是合理的。

因此,本文总结上述规律得出结论,采用固定算法求候选集合,在计算分水比的过程中,当运算到一定程度时,随着运算组数的增加,总缺水量呈现周期性变化的规律；且步长越小,周期的长度越长,但周期内总缺水量的最小值越小,不同周期内总缺水量最小值的差在一个固定范围内。由此,本文提出了分布式算法来求0.01的分水比。首先计算步长0.02的不同周期内总缺水量的最小值,选择步长0.02总缺水量最小的分水比作为起点,将步长设置为0.01继续向后计算,在一个周期结束的时候,即可得出本周期内的最小值。

3.2 计算分析

基于以上结论,步长为0.01时总缺水量的变化周期要长于步长为0.02时的周期,周期内步长0.01对应的总缺水量的最小值要更小,且周期内曲线的下降速率更小。而不同周期内总缺水量最小值的差值要小于20万m3。所以,当计算到第2个周期时,一次计算的结果与总缺水量最小值的差大于20万m3,则该结果一定不是此周期内的总缺水量最小值,且周期内步长0.01的曲线下降速率更小。因此,如果差值大于100万m3,直接跳过500组候选集合中的数据;依次递减,如果差值大于60万m3,则跳过100组数据;差值大于50万m3,则跳过10组数据,以便简化计算。经过计算,可得步长为0.01时的总缺水量极小值为111 255.42万m3,不同周期内最小值的差小于10万m3。取1 400余组运算数据进行展示,如图6所示。

图6 步长为0.01的总缺水量变化趋势(1 400余组运算数据)

采用同样的方法嵌套计算,即可求出步长0.001时的最优分水比。考虑时间效益最大和缺水量最小,记录下第2个周期内跳过的数据组数;当开始计算第3个周期时,直接跳过相应组数以简化计算;当连续3个周期内缺水量最小值的差在3万m3时,就不再继续计算,取计算结果的最小值对应的分水比为最优分水比,最终只需要进行约105次计算。这样,就得到步长0.001的总缺水量极小值为111 129.65万m3,东宝区、掇刀区、沙洋县、钟祥市、荆州区、当阳市对应的分水比分别为0.013、0.047、0.506、0.007、0.399、0.028。取3 000余组运算数据进行展示,如图7所示。

图7 步长为0.001的总缺水量变化趋势(3 000余组运算数据)

按文中所得的分水比,可计算出过去43 a的供水情况,并与实际供水情况对比,如图8所示。

图8 43 a的年缺水量对比

由图8可以发现：使用本文计算的分水比供水,年缺水量大于过去值的,只有4 a;年缺水量与过去值相等且保持为零的,有3 a;年缺水量小于过去值的,有36 a,年缺水量减小的范围为126.31～5 099.54万m3;年缺水量为零的年份较多,共29 a;43 a的总缺水量比过去的179 788.07万m3减少了68 658.43万m3,符合整个水资源分配体系总体效益最好的原则。

最终,可计算出漳河水库连续供水43 a的时段库容变化规律,如图9所示。通过观察图9可以发现,漳河水库时段库容变化曲线整体呈现周期性变化规律。掌握漳河水库的库容规律,可给未来保证水资源的供需平衡、制定供水策略和节水规划等提供有力的依据。尤其在供水时,在漳河水库时段库容较大的月份,可以适当减少前置水源的供水量,增加前置水源的可利用量,让漳河水库适当多供水,减少弃水;当漳河水库时段库容即将达到死库容的月份,让前置水源全力供水,前置水源供量不够的由漳河水库供水,以实现减少缺水量的目的。

图9 漳河水库时段库容随供水月数变化曲线

4 结语

为了解决基于规则的水资源合理配置水库最优分水比的计算问题,本文利用数据挖掘的思想,融合大数据技术,通过挖掘数据隐藏的规律,从中找出数量特征和数量关系,提出了分布式算法并验证了其有效性。该算法可以有效减少数据的运算次数,将分水比的计算分步进行,且在后续计算中,依靠先验经验,根据一次计算结果与周期内最小值的差大于一个阈值,跳过一定数量的候选数据,以便简化计算,从而切实有效地计算出步长为0.001的最优分水比。分布式算法的提出,给规则较为复杂、多供水源、多用水单元,且存在一定空间复杂度的水资源配置过程的水库最优分水比的计算找准了方向,也为其他地区的水库分水比计算提供了参考。