供水管网爆管率预测与影响因子分析
戴雄奇,王博彦,林 峰,常 田
(1.深圳市水务(集团)有限公司,广东深圳518031;2.中国石油化工股份有限公司北京化工研究院,北京100013)
供水管网是城市不可或缺的基础设施,具有隐蔽性、变化性大、复杂度高、材质多样性等特性。爆管事件的频发,对人民生活、工业生产、城市供水安全等带来较大危害。城市供水管网存在例如管线老化严重、管理水平落后等问题,严重影响供水系统的安全运行。爆管事故不仅增加了企业的供水成本,还会损坏公共设施,妨碍交通,影响生活和生产秩序[1]。
管网发生爆管事故通常是内外因综合作用的结果,影响因素众多且复杂,大体上可分为物理因素(例如管径、管材、管长、建设时间等)、环境因素(例如路面状况、覆盖面土质等)和运行状况(例如水压、维修记录等)三大类[1-2]。通过整合供水管网基础数据和运营数据,构建供水管网数据库,以大数据分析算法为基础建立爆管预测模型,从而对供水管网爆管率进行预测,并形成完善的供水管网资产优化管理体系,有助于为供水管网的更新和改造提供决策依据[2-3]。
1 模型算法的原理
目前,现有的管线评价多采用模糊理论、多元线性回归、层次分析法等方法建立模型,存在主观性较强、对数据质量要求高、适用于特定管网等不足。考虑到多数供水企业信息化程度较低,存在历史数据记录不完整、数据准确率不高、缺乏统一标准等问题[4],这些方法并不适合供水管网爆管模型分析[5-6]。
为了建立一个对数据质量要求低、适用范围广、准确性较高的供水管网爆管率预测模型[7],笔者采用机器学习方法,利用随机森林算法建立模型,对城市供水管网爆管率进行预测。随机森林是一种使用自助抽样方式,随机特征子集和采用投票进行预测,由多棵无关联决策树构成的模型系统。决策树是根据数据的特征构造的树状结构,当输入新的特征时,可以根据其构造好的结构做出一步步判断,最后得到分类结果[7-8]。
2 模型的建立
2.1 建模技术路线
模型建立的技术路线和流程见图1。
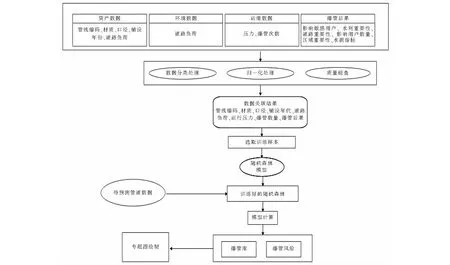
图1 建模路线Fig.1 Modeling routing
2.2 数据准备
从供水管网的基础数据库中提取管线的基础信息,包括管材、管线编号、管长、管径、建设年份、运行压力、地理位置、道路负荷、杂散电流、土壤腐蚀等;从城市供水管网的爆管数据库中,提取爆管管线编号、爆管时间、爆管原因、爆管类型、爆管点坐标等信息。对获取的数据依据以下原则进行预处理。
2.2.1 数据筛选
剔除非自然因素(第三方、人为)导致事故的爆管记录,修正录入错误,剔除明显异常数据。
2.2.2 数据库关联
将供水管网的基础数据库和爆管数据库按照管线编号或者空间位置进行关联,匹配获得每根管线的历史爆管信息。
2.2.3 确定影响因子
为保证数据的准确性及完备性,选择管龄、运行压力、管径、杂散电流、管材、道路负荷这6个基础属性作为发生爆管状况的影响因子。
2.2.4 数字编码
如表1所示,按照因子的数据属性将其划分为分类变量、连续变量两类,将分类变量数字化编码以便于代入模型运算,不同数字代表不同的数据类别。对于管线的历史爆管信息,用0表示管线未发生过爆管,用1表示管线发生爆管。
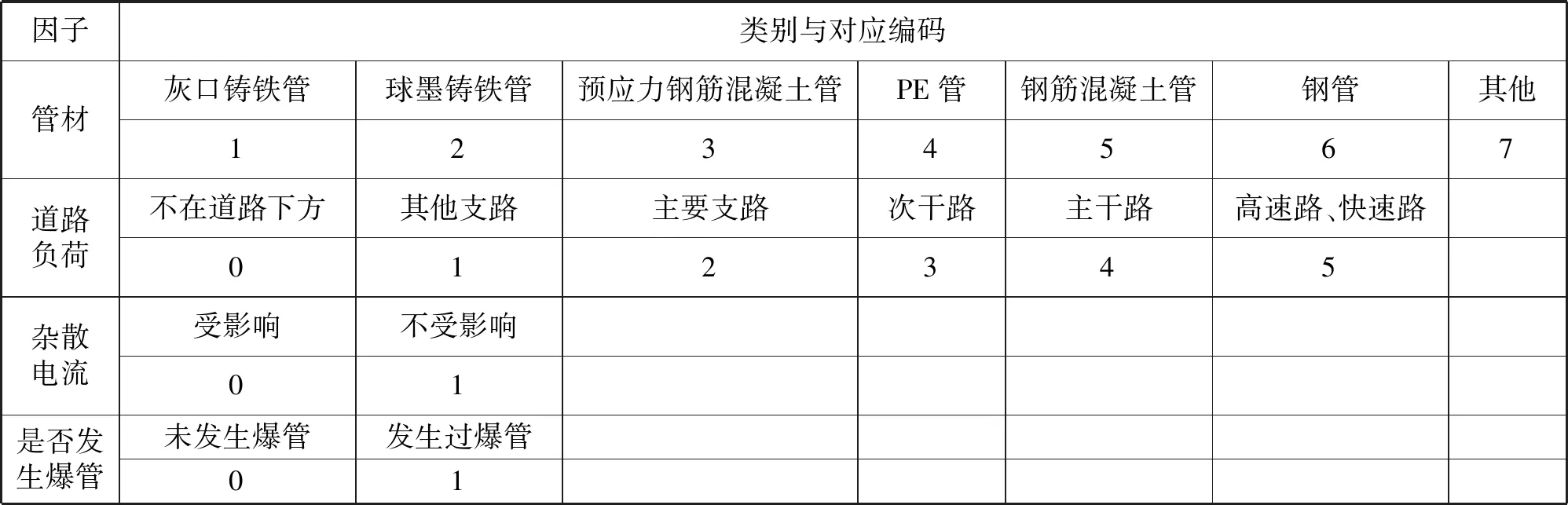
表1 分类变量数字编码对照Tab.1 Comparison of numeric encoding of classification variables
表1中,道路负荷依据属性划分为分类变量,将其数字化编码代入模型运算。道路负荷是基于该地区综合交通图来定义每条路段的负荷,若在某路段下方铺设管道,则把道路类型值赋给该管线;设铁路、地铁10 m范围内为杂散电流的影响区域,若管线安装在该区域内,则认为该管道可能会受到杂散电流的影响。预处理后的数据集示例如表2所示。
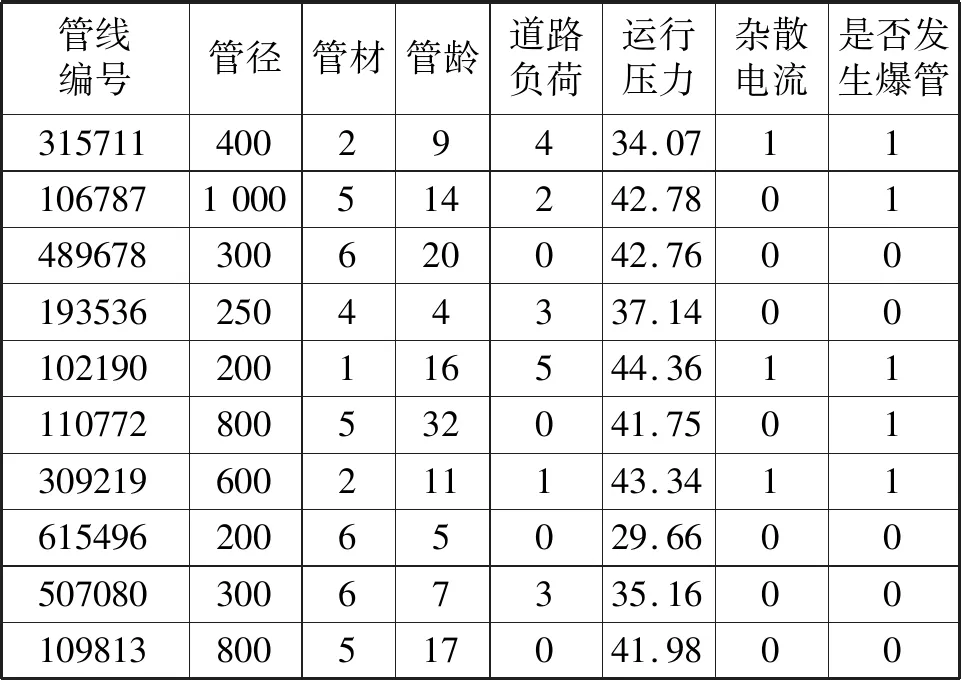
表2 管线数据集示例Tab.2 Sample pipeline data sets
2.3 模型建立
应用R软件建立模型,采用其中的Random Forest功能包。采用正、负样本两种方式选取样本,样本量比例为1 ∶1,即随机选取1000个爆管数据(正样本)和等量的未发生爆管的管线数据(负样本)。在模型训练使用的输入参数中,将管龄、运行压力、管径、杂散电流、管材、道路负荷6个影响因子定为自变量,管线是否发生爆管设为因变量。模型的输出结果为管线发生爆管的概率,是介于[0,1]之间的数值。
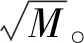
2.4 模型效果
在校验模型精度时,通常采用接收灵敏度曲线(receiver-operating characteristic,ROC)和曲线下面积(area under curve,AUC)来表示。AUC值越趋近于1,模型效果越好。当AUC值在0.5~0.7时,准确度较低;当AUC值在0.7~0.9时,准确性较好;当AUC>0.9时,准确性很高。
为了更加全面、客观地评价模型效果,采用ROC曲线综合检验模型的精度和稳定性,如图3所示,图中粗线表示检验结果和其变化范围。研究中,AUC平均值达0.85,模型准确性较为理想;箱线图显示,ROC曲线的变化幅度非常小,分布较为聚集,模型相对稳定,不易因样本集随机选取的变化产生影响。因此整体来看,模型的效果较好。
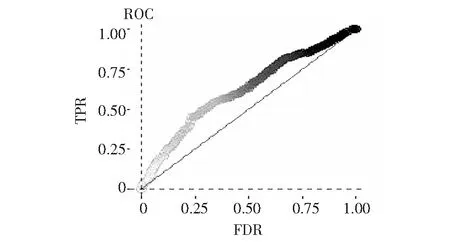
图2 ROC曲线Fig.2 ROC curve
3 模型应用
3.1 预测爆管概率
测评效果较好的模型可应用于其他研究区域。当利用数值表示分类变量(0代表未发生爆管,1代表发生爆管)作为因变量建立随机森林模型时,预测结果可得到发生/未发生爆管的概率,见表3。

表3 预测结果Tab.3 Prediction results
表3中最后1列数据为管网发生爆管的概率,倒数第2列表示管线不会发生爆管的概率。发生爆管的概率越趋近1,管网状况越差;概率越接近0,管网的健康度越高。
3.2 绘制专题图
为了使管网爆管率预测结果直观清晰,采用等间隔分类法,将状况评估结果分为健康(0~0.2)、较好(0.2~0.4)、一般(0.4~0.6)、较差(0.6~0.8)和危险(0.8~1)5个等级。
在ArcGIS中用不同的颜色展示管线健康状态分级结果,绘制出管网健康状态专题图,研究中随机森林模型评估专题图与实际情况的对比如图4、图5所示。两者的相似度较高,这表明所建立的随机森林模型的预测效果较好。
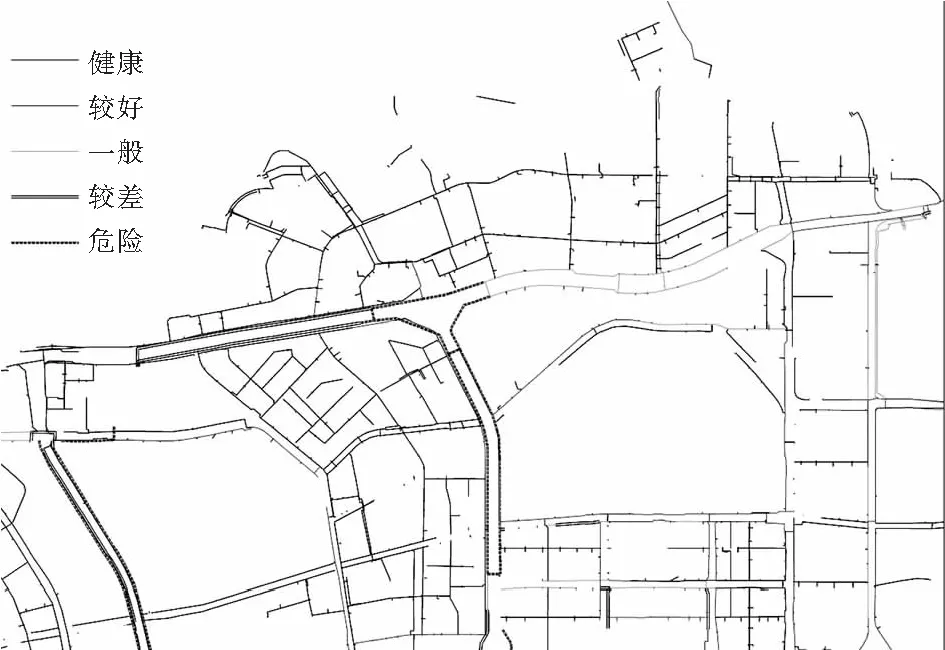
图3 资产状况评估Fig.3 Assessment of asset status
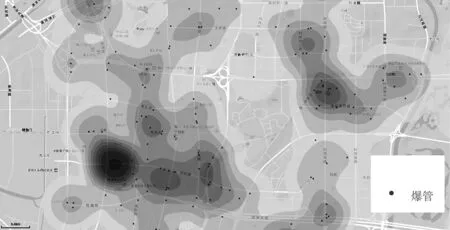
图4 资产实际状况Fig.4 Status of asset
4 影响因子分析
管线爆管的影响因子的重要程度,可通过图形的方式分析对比得出。衡量因子重要性的参数有2个:一是平均精度下降(mean decrease accuracy),对1个因子随机赋值,记录此时模型预测准确度的减小幅度,幅度越大则表明该因子越重要;二是平均基尼指数下降(mean decrease Gini),利用基尼指数记录因子对决策树的节点不纯度的降低程度产生的影响,值越大则反映出该因子越重要。其中,2种参数对比得出的因子重要性会略有差距,但差距很小,不会影响对结果的判断。
分别用上述2类方法对6个影响因子进行重要性评价,如图5所示。结果表明运用2种方法得出的因子重要性的排序结果基本一致,其中运行压力、管龄是发生爆管的主要影响因子,杂散电流对爆管的影响程度最小。通过因子的重要性排序,剔除影响较小的自变量,可以优化爆管模型;同时筛选出重要性因子,在数据收集工作中可将其作为重要指标,提升数据质量。
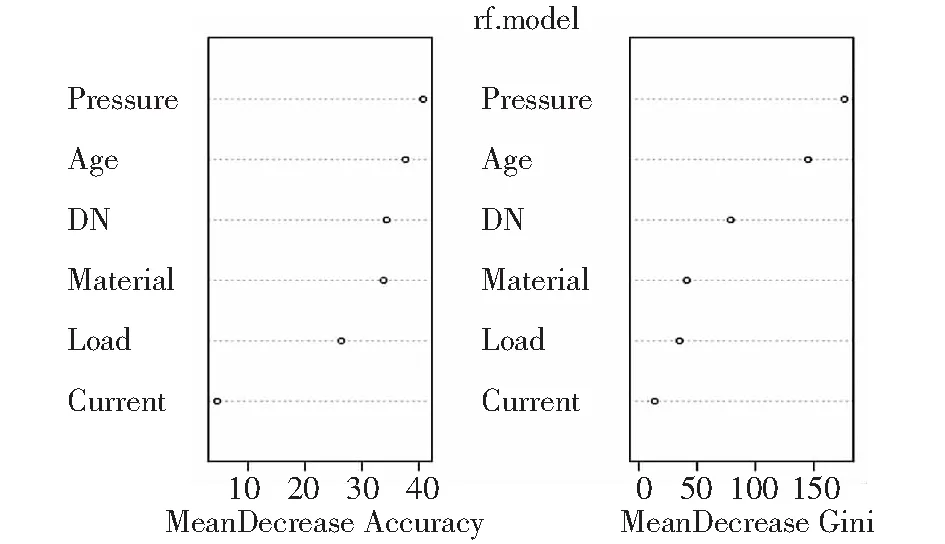
图5 因子重要性评价Fig.5 Importance evaluation of factors
5 结论
供水企业可根据模型预测结果制定管线更新改造优先次序和维修养护计划,利用爆管预测图对高爆管率的区域安排重点巡检,并重点监测管龄和运行压力这2个影响因子,实现供水企业对供水管网更新改造资金优化,且做到爆管提前预警、科学防范,为供水管网科学化、智能化管理夯实基础。

