城市轨道交通高架桥箱梁结构振动特性分析

罗 锟，张新亚，雷晓燕

(华东交通大学铁路环境振动与噪声教育部工程研究中心，南昌 330013)

近些年，轨道交通凭借其运量大、快捷、安全的特点得以快速的发展。高架桥作为城市轨道交通土建工程的重要组成部分，具有工后沉降低、节约土地、建设周期短等诸多优点[1-2]。然而列车通过桥梁引起的结构振动问题日益突出，并且轮轨作用激起的桥梁振动还会向四周辐射低频噪声，研究表明桥梁低频结构噪声向四周传播时，衰减慢、穿透力强，更容易给沿线居民的生活带来长期性的干扰[3-5]。因此开展桥梁结构振动规律的研究，对于桥梁减振降噪措施的设计、促进高架轨道交通的发展具有重要意义。

随着人们环保意识的增强，国内外学者开展了大量的工作来研究车桥耦合振动问题。国外Crockett等建立了车辆-轨道-箱梁的有限元模型，并计算了轮轨相互作用引起的结构振动[6-7]。国内以翟婉明、雷晓燕和夏禾为代表的团队建立了车桥动态相互作用模型，研究了桥梁振动对行车稳定性以及对周边环境的影响，取得了大量的研究成果[8-11]。李奇、李小珍等学者还采用现场测试的方法进行了桥梁振动与噪声研究[12-14]。此外，ANSYS、ABAQUS等商业有限元软件以及SIMPACK等多体动力学软件的出现，为车桥耦合振动问题的解决提供了一种新型、有效的途径[15-17]。雷晓燕等[18-19]总结分析以往利用SIMPACK软件建立的仿真模型，提出了一种轮轨耦合联合仿真方法，并据此建立了城市轨道交通车桥耦合振动模型，分析了列车过桥时简支梁桥结构振动问题。

为了研究轨道箱梁结构在列车通过时的振动响应及分布特性，以32 m简支箱梁桥为研究对象，基于车桥耦合动力学分析模型，利用多体动力学与有限元法求解分析箱梁结构的振动响应特性，研究了车致结构振动在桥梁横向与纵向的分布规律，以期为城市轨道交通高架箱梁结构的减振降噪设计提供依据。

1 轨道箱梁结构振动分析模型

1.1 车辆模型

车辆模型选取地铁B型车计算，利用多体动力学软件UM建立，将其考虑为多刚体系统[20]。为了减少计算时间，仅建立2节列车进行加载，每节车厢均由2个转向架、4个轮对组成，根据实际列车参数建立车体、转向架、轮对模型，并完成组装，如图1所示。

图1 车辆模型

1.2 轨道箱梁结构有限元分析模型

某城市轨道交通箱梁结构标准跨径32 m，采用C50混凝土材料浇筑，桥面宽12 m。在ANSYS中建立轨道箱梁结构三维有限元模型，如图2所示。模型包括钢轨、轨道板、CA砂浆层、混凝土底座和箱梁梁体，如图3所示。其中箱梁、混凝土底座和轨道板采用实体单元模拟，钢轨选用梁单元进行模拟，扣件、CA砂浆层以及桥梁支座均选用弹簧阻尼单元进行模拟，具体计算参数取值见表1和表2。

图2 轨道箱梁结构有限元模型

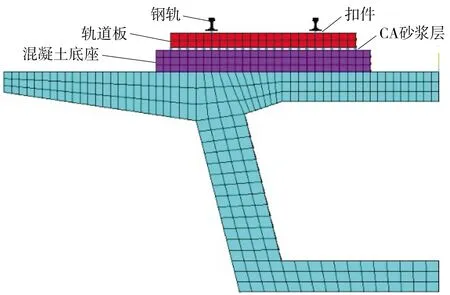
图3 轨道结构部件

表1 结构部件主要计算参数

表2 连接部件计算参数

2 轮轨激励的求解与测点布置

2.1 轮轨激励的求解与加载

基于多体动力学软件UM建立的地铁B型列车，并采用UM中的柔性轨模块Flexible Railway Track建立钢轨子系统[21]，将钢轨等效为铁木辛柯梁模型。仿真列车在轨道上运行，并提取轮轨作用力如图4所示。仿真求解时轨道不平顺类型选用德国高干扰谱，波长范围0.1～30 m。利用2节列车加载，计算速度为80 km/h。

将计算得到的轮轨力看作是一系列随着时间变化的移动荷载，通过在ANSYS软件中利用APDL语言编写DO循环，采用节点加载的方式，将轮轨力时程加载到高架桥梁上，实现列车过桥的模拟。

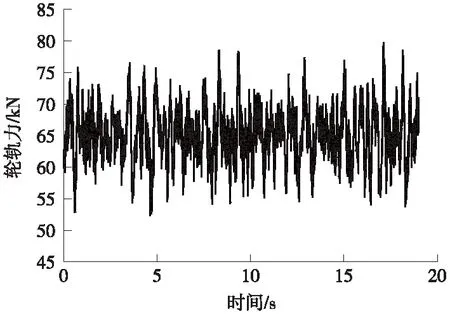
图4 轮轨力时程曲线

2.2 测点的布置

沿列车的前进方向选取3个截面：梁端截面、1/4截面和跨中截面作为观测截面，如图5所示，其中每个截面分别在钢轨(C1)、轨道板顶面(C2)、混凝土底座板顶面(C3)、底座板底面(C4)、梁体顶板(C5)、翼缘板(C6)、腹板(C7)和底板(C8)共布置8个测点，如图6所示。

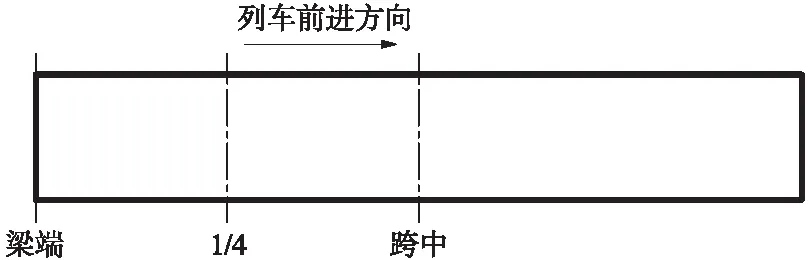
图5 箱梁桥观测截面

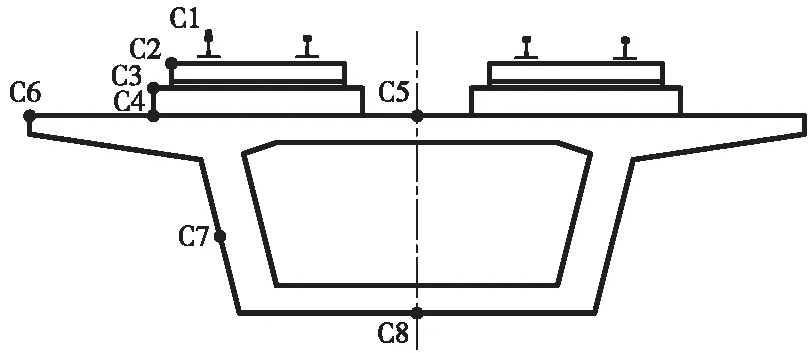
图6 观测截面特征点布置

3 轨道箱梁结构振动响应分析

利用上述车桥耦合振动分析模型，仿真分析振动响应在各个截面以及各板件的分布特性。计算车速为80 km/h时，列车通过时间为3 s。

3.1 梁上轨道结构

仿真分析提取梁上轨道结构各部件的振动加速度响应，并绘制跨中截面梁上轨道结构各部件振动加速度级的1/3倍频程谱图，如图7所示。从图7可以看到：在箱梁桥的钢轨、轨道板、混凝土底座板、梁体等结构中，钢轨的加速度响应最大，轨道板上的响应次之，底座和梁体最小，体现了振动从钢轨经由扣件向轨道板的衰减，从轨道板经由CA砂浆层向混凝土底座的衰减。

图7 跨中各结构部件振动加速度级的1/3倍频程谱

其中扣件在全频段内具有减振效果，特别在70 Hz以上的中高频范围，振动由钢轨向轨道板的衰减非常大，最大频段可减振40 dB。而CA砂浆的减振效果不甚明显，最大仅可在16 Hz频率附近减振2～3 dB。

3.2 梁体

提取梁体各板件的振动加速度数据，并绘制跨中截面梁体各板件加速度时域曲线如图8所示，对时域数据进行频域变换并绘制跨中截面梁体各板件振动加速度级的1/3倍频程谱如图9所示。

从图9可以看出：梁体振动的优势频段在6.3～63 Hz，最大振动加速度级在翼板位置为100.9 dB。振动沿横向梁体各板件传递过程中，翼板加速度响应最大，腹板次之，顶板和底板相对较小。表明振动由顶板向翼板的传递过程中，加速度响应放大。而顶板和底板的响应接近，也体现了振动由翼板向腹板，再从腹板向底板传递过程中的衰减。

图8 跨中截面梁体各板件加速度时域曲线

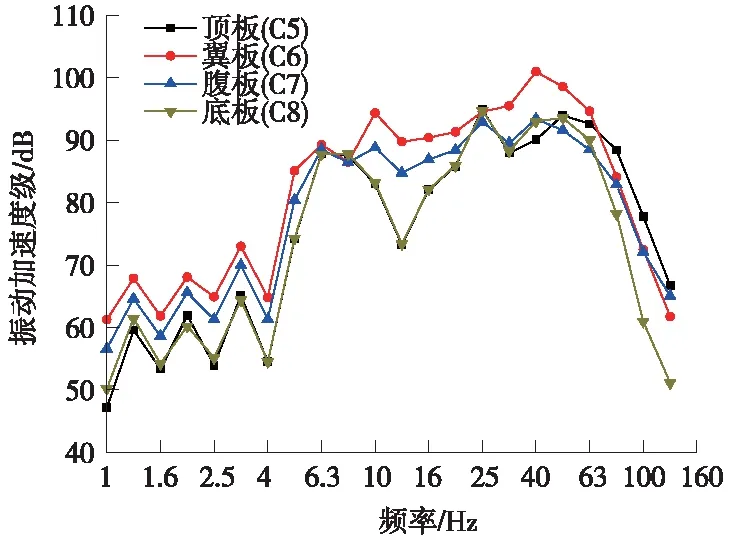
图9 跨中截面梁体各板件振动加速度级的1/3倍频程谱

图10(a)、图10(b)分别给出了箱梁梁体各截面观测点竖向振动响应的最大位移值与最大加速度值。

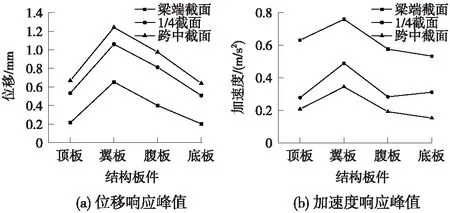
图10 各板件振动响应

可以发现：当列车以80 km/h的速度过桥时，跨中截面的位移响应最大，1/4截面次之，梁端截面的位移响应最小，这是因为桥梁支座的约束限制了梁体的位移发展。梁端截面的加速度响应最大，1/4截面次之，跨中截面的加速度响应较小。

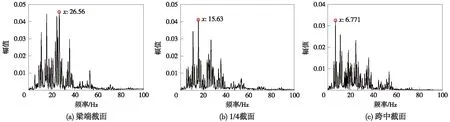
图12 翼缘板测点加速度频谱曲线

而通过最值分析也可以看到，各观测截面均以翼板振动响应最为强烈，其次是腹板。由此在进行高架轨道箱梁结构振动与噪声的控制时，应将箱梁翼板、腹板的振动控制作为主要关注点。

如图11所示，以箱梁翼板为观测对象，从列车上桥到列车下桥过程中，提取不同截面位置的翼板观测点位移曲线，可以发现跨中截面的位移发展速度最快，1/4截面次之，梁端截面位移发展速度较慢。而且可以发现3个截面的翼板观测点位移曲线线型近乎一致，并均在1.75 s达到位移响应的最大值1.24 mm。

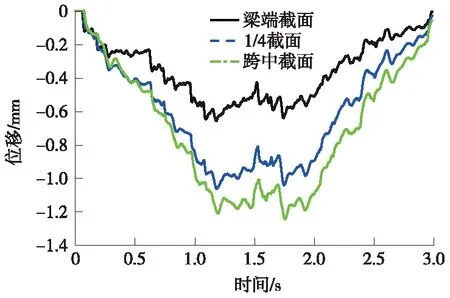
图11 不同截面翼板位移时程曲线

提取列车荷载作用下，3个观测截面下翼板观测点的振动加速度响应，并对翼板加速度响应时程数据进行FFT变换，得到各截面翼板的竖向加速度频谱曲线，如图12所示。

结合轨道箱梁结构模态分析结果，可确定对不同截面振动响应贡献较大的模态，并为箱梁桥的振动控制提供设计依据，比如在进行箱梁多阶模态TMD控制时，可为TMD悬挂位置设计提供依据。其中模态分析得到箱梁竖向振型贡献率较大的模态频率如表3所示。

从图12可以看出，列车80 km/h运行速度下，竖向加速度响应主要集中在0～40 Hz，且加速度峰值频率附近均有模态频率与之对应。其中梁端截面的峰值频率为26.56 Hz，在3阶竖弯振型频率附近，而3阶竖弯振型的波腹在梁端，因此3阶竖弯模态对该截面位置振动响应贡献最大；1/4截面的峰值频率为15.63 Hz，在2阶竖弯振型频率附近，而2阶竖弯振型的波腹位置在1/4截面位置处，因此2阶竖弯模态对该截面位置振动响应贡献最大；跨中截面的优势频率为6.771 Hz，在一阶竖弯振型频率附近，而一阶竖弯振型的波腹为跨中位置，因此该位置1阶竖弯模态振动贡献最大。

表3 箱梁桥模态频率

4 结论

基于车桥耦合动力学分析模型，利用多体动力学与有限元法求解并分析轨道箱梁结构的振动响应规律及分布特性，得到以下结论。

(1)利用从多体动力学软件UM中提取得到的地铁B型列车轮轨力时程，在ANSYS有限元软件中进行加载，计算结果能较好地反应桥梁的动力特性。

(2)列车以80 km/h的速度过桥时，车致振动在沿轨道结构自上而下传递，扣件在全频段减振效果明显，CA砂浆层的减振效果不佳。

(3)箱梁桥的翼板竖向振动响应水平最大，腹板次之，顶板和底板较小，在进行桥梁振动控制研究时应该重点关注翼板和腹板振动。

(4)箱梁桥的不同截面，模态贡献呈现差异，3阶竖弯对梁端截面的振动响应贡献最大，2阶竖弯振型对1/4截面振动贡献最大，跨中截面以1阶竖弯振动贡献为主。