基于地应力侧压系数的青藏高原东南缘区域性岩爆预测研究
陈兴强
(1.中铁第一勘察设计院集团有限公司,西安 710043; 2.陕西省铁道及地下交通工程重点实验室(中铁一院),西安 710043)
1 研究背景
2017年国务院发布了“十三五”现代综合交通运输体系发展规划,未来会有一系列铁路、公路交通工程在西部青藏高原山区建设。这些交通工程一般标准较高,需设计大量深埋长大隧道。因受印度板块与欧亚板块持续挤压碰撞影响[1-2],青藏高原东南缘地区(简称藏东南地区)大地构造背景复杂、活动断裂发育、地震活跃、高差极大(图1)。在此背景下,这一区域隧道工程往往具有埋深大、地应力极高、岩爆突出的典型特征[3-11]。因此该区域交通工程建设过程中,有必要从大范围工程选线选址,到勘察设计,再到施工的全过程对高地应力及其引起的岩爆进行分析预测与监测预警。
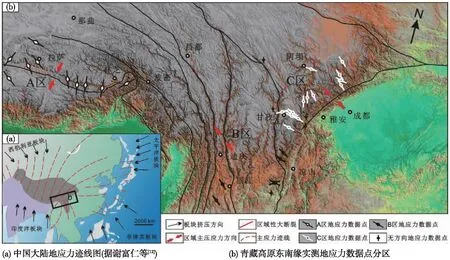
图1 青藏高原东南缘地区大地构造示意
高地应力及其引起的岩爆问题由于发生在地下工程,其认识程度往往随着工程勘察、施工的推进和资料的丰富而逐步提升。在施工过程中,可以进行洞身位置的原位地应力测量和岩爆微震监测等研究[13-14];在详细勘察设计过程中,可以在大量探至洞身的深孔内进行山体地应力的测量[4,15]。上述两个阶段地应力测试、监测的空间尺度一般为数米至数千米,可采用相关软件对地下工程的地应力进行有效的三维数值模拟分析,并将其有效应用到岩爆分析之中[3,5,16-17]。
然而,在大范围工程选线选址、初步勘察等初期阶段,是无法开展洞身、深孔地应力实测的。即使搜集到部分实测数据,也无法开展足够精度的数值模拟工作。为有效应对初期阶段对地应力和岩爆分析的需求,本文基于侧压系数理论,对藏东南地区进行了分区地应力分析和模拟。并以此为基础,对各分区一定深度范围的地下工程潜在岩爆等级进行了预测。
2 侧压系数理论及计算推导过程
影响地壳应力状态的因素有很多,使得地壳应力呈现非均匀分布。因此,利用不同地区原地应力实测数据得到的应力随深度变化的回归分析结果不尽相同。垂直应力外随深度显示出明显的线性变化外,最大水平主应力和最小水平主应力都只在一定的深度(几百米)范围内呈线性变化;更大深度范围的地应力模拟和预测,则需进行分段模拟[18],否则误差极大,需要采用其他更为合理的方法。
1978年,E.T.Brown和E.Hoek[19]总结归纳了世界不同地区地应力的测量数据,结果显示平均水平地应力与垂直地应力比值随深度变化呈现双曲线特征,并绘制了Hoek-Brown内包线和外包线。景锋等[18]认为采用SH/SV、Sh/SV更能反映我国水平构造应力场的差异性特征。这些论断反映出同一地区/构造背景下,深度对地应力结果的影响。另一方面,考虑到硬质岩地应力相对软质岩类更为稳定,可以根据特定地区的少量硬质岩内实测数据对整个区域的地应力进行预测,进而利用其对区域性岩爆进行分析。
实际上,根据水平最大和水平最小主应力随深度呈线性增加这一得到广泛认可的结果,可以从数学上建立其他应力参数随深度变化的关系式,包括平均水平应力与垂直应力之比(Save/SV)、水平最大主应力与垂直应力之比(SH/SV)、水平最小主应力与垂直应力之比(Sh/SV)等。
平均水平应力与垂直应力随深度变化[20]的关系
Save=aave×Z+bave
(1)
则水平最大主应力和水平最小主应力随深度变化的回归关系式可描述为
SH=aH×Z+bH
(2)
Sh=ah×Z+bh
(3)
垂直应力随深度变化的回归关系式可描述为
SV=aV×Z
(4)
其中,垂直应力参考系数aV一般直接用上覆岩层的重力来估算,对于同一岩性,接近一个常数,片麻岩、花岗岩等一般取0.027,而固结较好的砂岩、泥岩等一般取0.026,在进行区域计算时使用其平均值0.026 5即可。前文已述及,侧压系数可以表示为
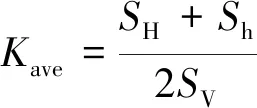
(5)
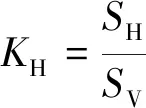
(6)
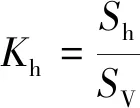
(7)
由此,在aV数值稳定的情况下,Z深度点的Save、SH、Sh的计算,就可以转换为对Kave、KH、Kh的计算。将式(1)~式(4)代入式(5)~式(7),变换可得
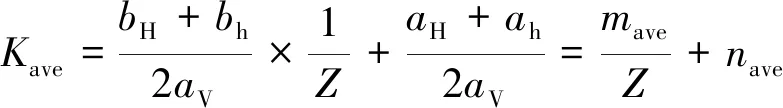
(8)
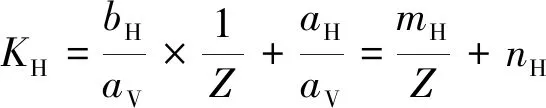
(9)
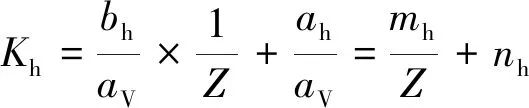
(10)
式(8)~式(10)均是双曲线函数,在aV数值稳定的情况下,mave=(bH+bh)/(2av),nave=(aH+ah/(2av),mH=bH/av,nH=aH/av,mh=bh/av,nh=ah/av均为常数。进一步,Z深度点的Save、SH、Sh的计算,则转换为对mave、nave、mH、nH、mh、nh的获取。
上述推导过程表明,使用侧压系数公式进行一定深度地应力推算是可行、有效的。参数mave、nave、mH、nH、mh、nh等需依据岩体的完整性、弹性模量、岩体强度参数、岩体抗拉强度、岩体抗压强度、黏聚力、内摩擦角等综合确定[21],勘察初期获取难度较大。但是,当有实测数据的情况下,可以直接通过实测数据按K=m/Z+n的公式进行数据拟合,进而反推mave、nave、mH、nH、mh、nh等参数值,这种情况避免了各类参数进行换算的过程。
3 藏东南区域地应力侧压系数模拟
本次共收集500余组水压致裂法地应力测量数据,主要来自于铁路、公路、水利水电等工程,如拉林铁路[3,22]、成兰铁路[7]、川藏公路[6]、锦屏水电站[8]等,因文献过多,在此不一一列举。考虑到断裂破碎带条件会对地应力大小和方向产生明显的影响[23],岩爆主要发生在硬质岩中,最终计算时,排除了100余组明显受断裂带影响的、非硬质岩内测量的数据。
藏东南由西向东表现为明显的由挤压构造(雅鲁藏布江缝合带影响区-藏东南A区)向走滑构造(三江构造带影响区-藏东南B区),再向挤压构造(龙门山构造带影响区-藏东南C区)转换的特征(图1)。据此,将藏东南划分为三大区块进行侧压系数综合模拟,分别对其平均值、内包线和外包线进行了模拟。其中A区79组数据,B区112组,C区224组。
模拟结果表明,藏东南A、B、C 3个分区测压系数均符合K=m/Z+n的双曲线特征,最大水平主应力侧压系数均值分别为KH=120/Z+0.95,KH=562/Z+0.52,KH=356/Z+0.75(图2);最小水平主应力侧压系数均值分别为Kh=110/Z+0.61,Kh=360/Z+0.25,Kh=248/Z+0.48;平均主应力侧压系数均值分别为Kave=115/Z+0.76,Kave=461/Z+0.43,Kave=302/Z+0.61。由图2可知,3个区域最大水平主应力侧压系数KH呈现以下统一的特点:(1)区域最大水平地应力与垂直地应力的比值随深度的变化规律,呈现出逐渐变小的趋势;(2)深度越大,模拟结果越接近实测值,在约400 m深度内,量测结果十分分散,600~1 000 m深度较为分散,1 000 m以上则较为集中,说明越接近地表,最大水平主应力受构造、地形地貌等影响越严重,对岩爆预测越不利;(3)与Hoek-Brown统计的世界范围内量测的平均值相比,均呈现出浅部低于世界平均值,1 200~2 000 m开始,超过世界平均值的特征。
3个分区之间的差异表现为:(1)1 000 m深度范围以内,A区地应力低于B区和C区,且呈现出A区
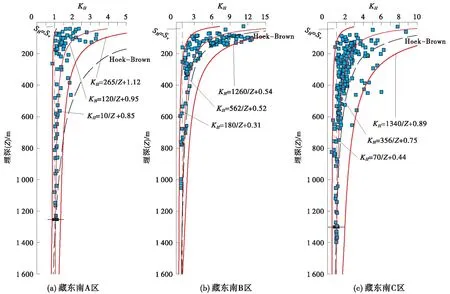
图2 藏东南各分区KH随深度变化及其与Hoek-Brown全球平均(黑色虚线)对比
4 基于侧压系数的区域岩爆预测分析
4.1 岩爆计算方法选择
在勘察设计阶段,岩爆的计算一般包括两大类方法。①不反映硐室开挖过程影响的方法:计算时考虑岩石抗压强度和围岩主应力,以强度应力比法为代表,如TB10003—2016《铁路隧道设计规范》、GB50287—2016《水力发电工程地质勘察规范》(表1)。②反映硐室开挖结构的方法:计算时考虑岩石抗压强度和硐室开挖后的切向应力,以应力强度比法为代表,如Turchaninov判据、Russemes判据等。两者相比较,后者计算过程相对较为复杂,且一般比前者计算的等级和段落要更高。同时,考虑到本文拟开展的区域性岩爆预测主要是为铁路、公路、水电站等勘测参考,本文以行业规范推荐的强度应力比法作为主要的分析方法。

表1 强度应力比法岩爆等级判别标准
注:σmax—围岩的最大地应力(SH>SV时取SH;SH Rc—岩石饱和单轴抗压强度。 研究区内主要出露的硬质岩类包括花岗岩、闪长岩等岩浆岩类,片麻岩等变质岩类,石英砂岩、灰岩等沉积岩类,各岩类常见密度及抗压强度范围见表2。综合考虑上述岩类抗压强度范围和平均值,以Rc=100 MPa(粗粒花岗岩、片麻岩、石英砂岩、灰岩等)、Rc=130 MPa(细粒花岗岩、闪长岩、石英砂岩等)两个等级的岩石抗压强度进行区域性岩爆趋势预测。 表2 藏东南地区主要岩性参数参考值 结合区域地貌特征,藏东南一般地区的山、谷的高差在3 000 m以内,即地下工程的最大埋深一般不超过3 000 m。以强度应力比法为基本计算方法,分别对Rc=100 MPa、Rc=130 MPa条件下、3 000 m埋深以内的岩爆等级与KH值的对应关系进行分区划分(图3),计算公式如下 (11) 该公式内含3个主要变量,Z、KH和SV,其中Z为深度,KH为Z深度时的侧压系数,SV为Z深度的垂直应力(Sv=aVZ)。同时存在3个常量,Rc为岩石饱和单轴抗压强度,分别取Rc=100 MPa、Rc=130 MPa;T为不同等级岩爆最小埋深的强度应力比值,参考表1,分别取7,4,2,1;参考表2,aV取0.0265。投图结果(图3)表明,深度Z、饱和单轴抗压强度Rc一致的情况下,KH越大,岩爆等级越高,直至当KH≤1时(此时,SH≤Sv),岩爆等级不再发生变化。饱和单轴抗压强度Rc越小,越容易发生岩爆,且等级越高。 图3 藏东南地区岩爆等级与KH值的对应关系投图 将模拟的藏东南A、B、C 3个分区的KH平均值拟合曲线投到图3(a)和图3(b)上,即可对不同分区、不同深度的岩爆等级进行大致的预测。从预测结果来看,考虑Rc=100 MPa和Rc=130 MPa的情况下,3个分区3 000 m以内都不会发生极强烈岩爆,而中等岩爆、强烈岩爆的埋深较为接近,轻微岩爆埋深差异明显。 Rc=100 MPa时,3个分区轻微岩爆的最小埋深分别为400,100,250 m。3个分区埋深超过800 m时可以达到中等岩爆。1 800 m左右A区可以达到强烈岩爆,而B区和C区由于在1 200,1 500 m左右侧压系数小于1,其强烈岩爆是否发生主要受控于垂直地应力,两者均在1 900 m左右达到强烈岩爆最小值。 Rc=130 MPa时,3个分区轻微岩爆的最小埋深都明显增大,分别为600,300,450 m。3个分区埋深为1 200 m左右时可以达到中等岩爆。2 400 m左右A区可以达到强烈岩爆。同样,由于B区和C区在1 200,1 500 m左右侧压系数小于1,其强烈岩爆是否发生主要受控于垂直地应力,两者均在2 500 m左右达到强烈岩爆最小埋深。 需要说明的是,上述分析,仅代表在这一岩石饱和单轴抗压强度(Rc)下最可能发生岩爆的最低深度值。由于搜集资料的不全面性、局部应力的差异、同一岩性抗压强度变化范围较大等因素影响,实际岩爆发生的深度范围会更大。如某些地应力较区域平均值明显偏高、岩石抗压强度偏低的情况,强烈岩爆仍可能发生。饱和单轴抗压强度Rc从100 MPa到130 MPa,各等级之间的深度差值可达到200~600 m,因此从精确的角度来讲,在有条件的情况下,应该实地采集新鲜岩石进行Rc试验。从保守的角度考虑,对于未受破坏的花岗岩、闪长岩等这类较好的围岩条件,可使用模拟获得的KH的外包线进行最大水平主应力的模拟。如A区,岩石饱和单轴抗压强度为100 MPa时,若考虑外包线,则轻微、中等、强烈岩爆的最低深度分别由400,1 800,2 400 m降低到250,700,1 500 m。 以侧压系数理论为基础,利用区域硬质岩地应力测量数据,对地应力背景值进行分析,是一种在大范围选线选址、初步勘察阶段岩爆灾害预测的有效手段。根据区域构造背景,藏东南地区可被划分为3个构造分区,分析结果表明。 (1)藏东南3个分区的侧压系数总体上符合K=m/Z+n的双曲线特征。其最大水平主应力侧压系数模拟结果分别为KH=120/Z+0.95,KH=562/Z+0.52,KH=356/Z+0.75。同一深度的K值满足A区>C区>B区的特征,与A区、C区为挤压、B区为走滑的构造背景相一致。 (2)以强度应力比法进行投图计算,在深度Z、饱和单轴抗压强度Rc一致的情况下,KH越大,岩爆等级越高,直至当KH≤1时,岩爆等级不再发生变化。该类图件可对任何地区的高地应力岩爆进行总体特征分析。 (3)基于平均地应力的岩爆投图分析,考虑Rc为100 MPa和130 MPa的情况下,藏东南地区中等、强烈岩爆的埋深较为接近,轻微岩爆埋深差异明显。其中危害较大的中等及以上等级岩爆起始埋深分别为800 m和1 200 m左右,因此在大面积选线和初步勘察阶段应注意降低该区域800~1 200 m以上深度的隧道长度。 由于岩爆是工程活动导致的,所有基于静态指标的结果都不能反映动态的施工过程和地质条件的变化。本文得出的岩爆发生等级预测仅为大范围选线选址、初步勘察设计阶段提供参考,在定测和施工阶段应采用原位地应力测试、微振监测等手段进行详细评价。4.2 主要岩石类型及其抗压强度参考值

4.3 岩爆分级投图
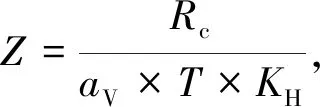
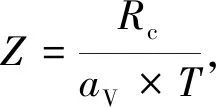

4.4 分析结果
5 结论与讨论
——以淮南矿区为例

