贝塔指数几何分布参数基于截尾样本下的极大似然估计及应用

李泽乙，李树有，宓 颖

贝塔指数几何分布参数基于截尾样本下的极大似然估计及应用

李泽乙，李树有，宓 颖

（辽宁工业大学 理学院，辽宁 锦州 121001）

研究了贝塔指数几何分布在截尾样本下的参数估计问题。给出分布中4个参数的极大似然估计，并运用牛顿迭代法给出参数极大似然估计的迭代计算公式。最后，利用铝片加工的实际观测数据取截尾样本下的观测数据，通过MATLAB编程计算，给出应用实例。

贝塔指数几何分布；截尾样本；极大似然估计；牛顿迭代法

贝塔指数分布(BEG)是由贝塔()随机变量的分对数产生的，是Adamidis等[1]提出的指数几何分布(EG)的扩展，且包括了广义指数几何分布(GEG)、几何指数分布(GE)，以及贝塔指数分布(BE)。Hmaid[2]于2012年给出BEG分布的累计分布函数、概率密度函数，并确定在参数取不同值时，BEG分布分别具有递减、递增和倒置的失效函数。

贝塔指数分布的累计分布函数为：

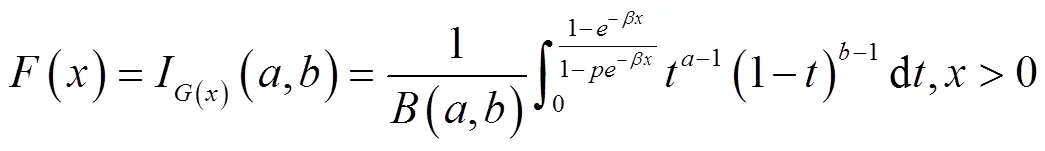
在已有研究基础上，本文给出了定数截尾样本[3]条件下贝塔指数几何分布4个未知参数的极大似然估计，结合牛顿迭代的方法给出了未知参数的极大似然估计的迭代计算公式。最后，依据铝片加工的疲劳寿命数据，利用MATLAB编程计算，得到分布中参数的极大似然估计值。

1 定数和定时截尾样本的概念

寿命分布及其数学描述对任意特定个体(产品或生物体)，从某个标准时间起在规定时间内失效(或死亡)，是一个随机事件。因此寿命是一个非负的随机变量，通常记为，其概率分布称为寿命分布。

寿命数据特点和寿命试验种类：一般的寿命数据与统计中通常使用的随机样本有很大区别。寿命数据往往是不完全数据，即并不是每一个观测到的值都是确切的寿命值。某些数据可能只表示相应个体的寿命不小于该数值，而并不知道其确切寿命的数值，这样的数据称为截尾数据。如从现场收集的寿命数据，由于在统计时某些产品尚未失效，或因多种原因中断观测，这些产品的实际寿命应比已观测到的时间长。就是在可以人为控制的产品寿命试验中，由于试验费时较长，费用较高，往往不能将试验进行到所有受试样品都失效时为止。因此必须在达到规定的时间或在失效的样品达到规定数目时终止试验。这种试验称为截尾试验[3]。前者称为定时截尾试验，后者称为定数截尾试验。

假设在时间=0时将随机抽取的个产品同时投入试验，当试验进行到有个(是事先规定的，<)产品失效时停止。其中个产品失效时间分别为：

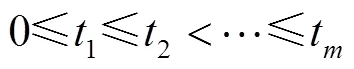
假设在时间=0时将随机抽取的个产品同时投入试验，实验开始前事先确定好截尾的时间0，当试验进行到事先规定的截尾时间0时停止。若到试验截止时一共有个产品失效，则它们的失效时间分别为：

科室的医生可以把自己的医嘱输入到医疗系统当中，护士在核对完成之后在通过使用网络传输的形式传达到病房的药房中[3]，工作人员同样需要通过计算机来确认收费信息后，进行库存的增减活动。工作人员要把信息打印成单子，在计算机中记录当天患者产生的药物使用费用。在药房管理工作中，药品清单可以分成为两种，分别是汇总单和明细单，这两种不同的模式可以根据购买需求进行切换，汇总单子是把药品进行了汇总，而明细单子则是按照患者的名字和床号等显示出了药物的具体信息，这样两种不同的清单模式，既能够帮助节省工作人员的工作效率，还能够提升发药的准确率。

2 贝塔指数几何分布参数在定数截尾样本下的极大似然估计

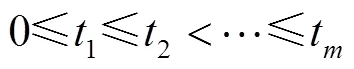
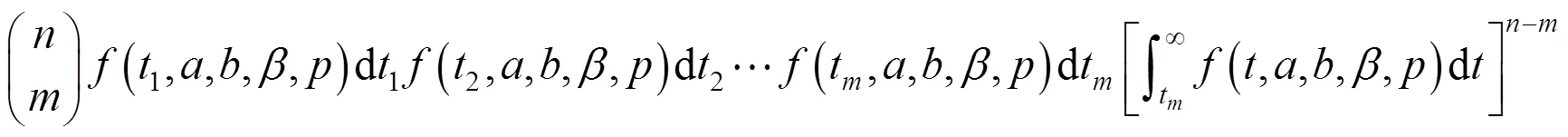
由分布参数的极大似然估计法可知，其似然函数为：

因而，其对数似然函数为：

考虑参数，，，均未知，求，，，的极大似然估计。对公式(3)对数似然函数中的，，，分别进行求导，联立方程并使其为零得到：

因为上述联立的方程不能有效地求出贝塔指数几何分布4个未知参数极大似然估计的显示解，所以采用迭代法计算未知参数的极大似然估计。令：

则有：

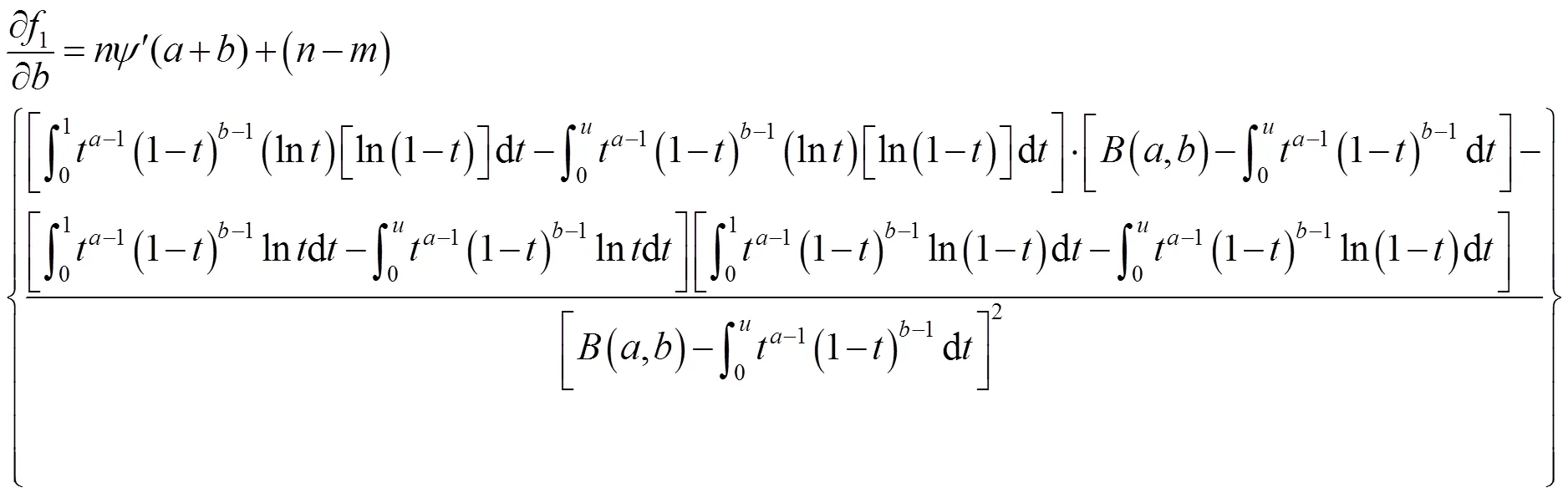
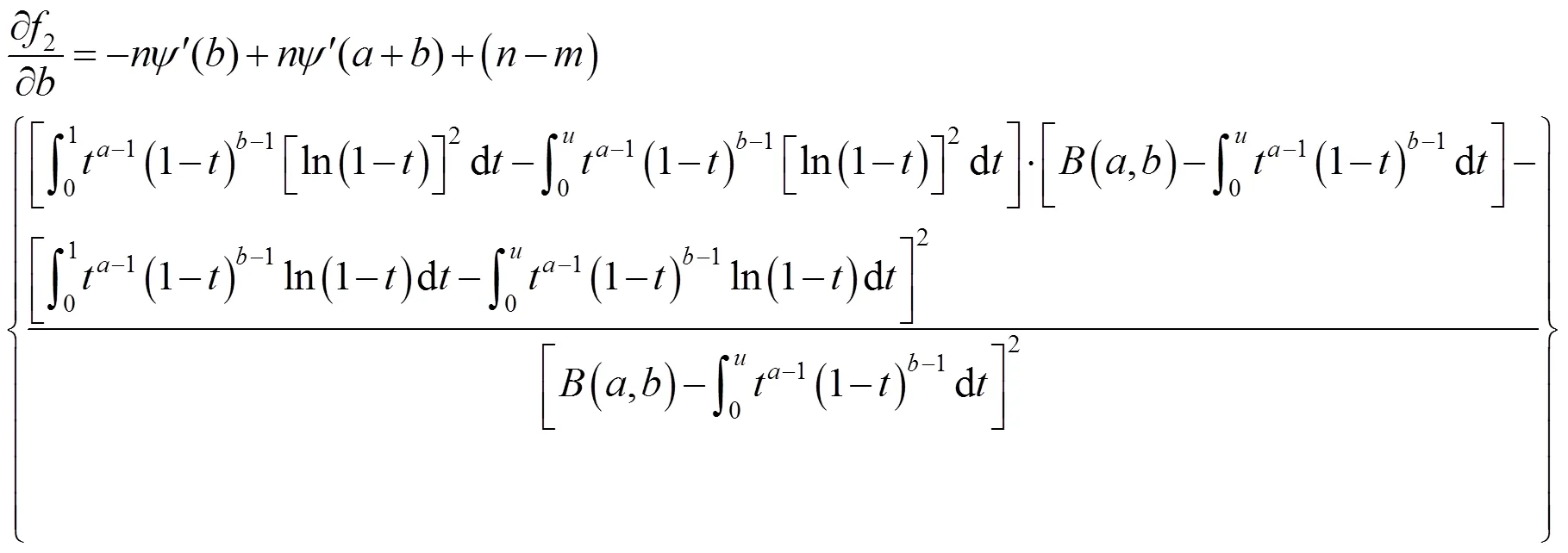
其中：

所以：

由牛顿迭代法[4]得到以下公式：

3 应用实例

考虑来自Birnbaum等[5]的6061-T6铝片与轧制方向平行在每秒18次震荡(每个周期最大应力为31 000 Psi)下的疲劳寿命的101个观测数据。规定试验进行有31个铝片失效时结束试验。则有投入定数截尾试验的铝片数为101，截尾数为=31。用MATLAB语言，代入数据，70，86，90，94，90，96，97，98，99，100，103，104，104，105，107，108，108，108，109，109，112，112，113，114，114，114，116，119，120，120，120，得到未知参数，，，的极大似然估计值，如表2所示。

表1 a，b，β，p的极大似然估计值

4 结论

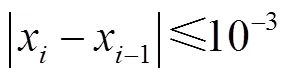
[1] Adamidis K, Loukas S. A lifetime distribution with decreasing failure rate[J]. Statistics and Probability Letters, 1998, 39: 35-42.

[2] Hamid Bidram. The Beta Exponential-Geometric Distribution[J]. Communications in Statistics - Simulation and Computation, 2012, 41(9): 1606-1622.

[3] 李树有, 徐美进, 刘秀娟. 应用数理统计[M]. 沈阳: 东北大学出版社, 2015.

[4] 颜庆津. 数值分析[M]. 北京: 北京航空航天大学出版社, 2012.

[5] Birnbaum Z W, Saunders S C. Estimation for a family of life distributions with applications to fatigue[J]. Journal of Applied Probability, 1969, 6: 328-347.

[6] Silva R B, Barreto-Souza W, Cordeiro G M. A new distribution with decreasing, increasing and upside-down bathtub failure rate[J]. Computational Statistics and Data Analysis, 2010, 54: 935-944.

[7] 李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2001.

[8] Barreto-Souza W, Santos A H, Cordeiro G M. The beta generalized exponential distribution[J]. Journal of Statistical Computation and Simulation, 2010, 80(2): 159-172.

[9] Eugene N, Lee C, Famoye F. Beta-normal distribution and its applications[J]. Communications in Statistics—Theory and Methods, 2002, 31(4): 497-512.

Maximum Likelihood Estimation of Beta Exponential-Geometric Distribution Based on Censored Samples and its Application

LI Ze-yi, LI Shu-you, MI Ying

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

The parameter estimation of the beta exponential-geometric distribution under the censored sample is studied. The maximum likelihood estimation of four parameters in the distribution is given, and the iterative formula of parameter maximum likelihood estimation is given by Newton iterative method. Finally, the observation data under the censored sample are taken from the actual observation data of aluminum sheet processing, and the application examples are given by Matlab programming calculation.

beta exponential-geometric distribution; censored sample; maximum likelihood estimation; newton iterative method

O212

A

1674-3261(2020)02-0133-08

10.15916/j.issn1674-3261.2020.02.016

2019-08-23

李泽乙(1992-)，男，辽宁大连人，硕士生。

李树有(1964-)，男，辽宁锦州人，教授，博士。

责任编校：孙 林