协调覆盖决策系统下基于三支决策的多类分类矩阵模型∗
夏秀云 田 浩 常安成 田时宇
(1.湖南信息学院通识教育学院 长沙 410005)(2.湖南信息学院电子信息学院 长沙 410005)
1 引言
Rough理论是近年来发展起来的一种数学理论方法,它可以处理含糊、不确定、不相容的知识。粗糙集理论在数据挖掘、模式识别、人工智能等方面都取得很大的成功[1~2]。三支决策理论是加拿大Yao.Y.Y在粗糙集和决策粗糙集基础上于2009年提出的新的决策理论,其是由决策粗糙集导出的分类规则,具有正域、负域和边界域的三区域特征[3]。目前三支决策理论已成功应用于多个领域。比如,Zhou等学者将三支决策应用到处理邮件文件中[4];Yao等学者探讨了三支决策在医疗网络支持系统的应用方法[5];之后,Liu、Li等学者从三支决策的视角出发,系统地介绍了三支决策与粗糙集理论融合的理论、方法和应用[6];张聪学者从树结构的角度出发,研究三支增量聚类算法模型[7];2017年,赵天娜等学者研究了基于多伴随直觉模糊粗糙集的三支决策模型[8];2018年,辛现伟学者通过使用可能性测度来度量直觉模糊的三支决策应用研究[9];2019年,徐久成等学者从二阶段出发,提出了基于三支决策的二阶段分类模型研究[10]。随后,刘丹等学者讨论了不完备邻域下多粒度决策理论粗糙集与三支决策的融合[11]。然而对于多类分类模型进行研究的文献不多。文献[12]中周等学者提出了一种多类分类模型,该模型考虑将误分类对象划分到不同决策类产生不同的损失函数,从而找出每个类的代价最小的行动决策,但该模型的最终结果可能存在决策冗余。后来,文献[13]中徐等学者针对决策粗糙系统提出了三支决策的多类分类模型。本文是在以上研究基础上提出来的,给出了基于协调覆盖决策系统的多类分类矩阵模型,从而获取最小的代价。首先给出协调覆盖决策系统和三支决策的有关定义,然后将延迟决策类的多类分类模型运用到协调覆盖决策系统中,提出了一种新的协调覆盖基于三支决策的多类分类矩阵模型,减少代价参数,降低决策风险,最后通过一个实例分析验证此方法的有效性和可行性。基于以上的讨论,本文为覆盖决策系统基于三支决策理论思想提供了新的框架,因此这样的研究是有意义的。
2 协调覆盖决策系统下的多类分类模型

定义3[15]设 π ={Ai:i=1,…m}是论域U 的一族覆盖集族,D是决策属性,UD是论域U上的决策 划 分 。 若 对 于 ∀ x∈U ,∃Ej∈UD ,使 得πx⊆Ej,则称决策系统 cds=(U,π,D)为协调覆盖决策系统。
定义 4[16]设 (U,A) 为一个覆盖近似空间,∀x∈U ,称





其中,三种行为下的期望损失可以分别表示为
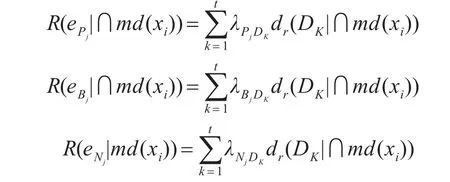
根据贝叶斯最小风险的决策准则,可以得到如下的决策规则:
(P):若 R(ePj|∩md(xi))≤ R(eBj|∩md(xi)),且R(ePj|∩ md(xi))≤ R(eNj|∩ md(xi)),则 xi∈ POS(Dj);
(B):若 R(eBj|∩md(xi))≤ R(ePj|∩md(xi)),且R(eBj|∩ md(xi))≤ R(eNj|∩ md(xi)),则 xi∈ BND(Dj);
(N):若 R(eNj|∩md(xi))≤ R(ePj|∩md(xi)),且R(eNj|∩ md(xi))≤ R(eBj|∩ md(xi)),则 xi∈ NEG(Dj)。
当然,在具体决策过程中,要求正确接受的代价损失小于错误拒绝的代价损失,延迟决策类的损失处于正确接受的代价损失与错误拒绝的代价损失之间。
3 基于协调覆盖的三支决策多类分类模型
定义12 设协调覆盖决策系统为ds=(U,π∪D,V,f),π={Ai;i=1,…,m}为 U 上一个覆盖集族,表示对象X的最小描述的交集是∩md(x),UD={D1,D2,…,Dt},则基于覆盖的三支决策的多分类模型的代价矩阵t×(t+1)阶的M1矩阵:

其中,M1延迟决策类的损失代价矩阵,其各列值是互不相同的,同时满足(t+1)列的各值小于λij(i∈[1,t],i≠j)的最小值。
与定义11相似,可得到基于协调覆盖的三支决策的多分类模型的决策风险矩阵定义如下。
定义13 设协调覆盖决策系统为ds=(U,π∪D,V,f),π={Ai;i=1,…,m}为 U 上一个覆盖集族,表示对象X的最小描述为∩md(x),UD={D1,D2,…,Dt},带延迟决策类的决策风险矩阵R1=Pπ×M1,记为


注:具体决策时,对∩md(x)所采取的决策要比较分析其不行动所付出的代价,找到最合理代价最小的行动。
4 实例与分析

表1 决策属性的误分类代价



根据定义11的决策规则可知:md(x1)∈POS(D1),md(x1)∈POS(D2),表示对于md(x1)而言既属于D1又属于 D2,这是一种决策冲突,md(x1)∈NEG(D3),表示该决策是多余的决策。下面我们引进延迟类决策代价来进行重新计算,比较两种方法的不同。隶属矩阵保持不变,注意从代价矩阵这里重新进行,由定义12可知:

根据定义13,计算出带延迟类的风险矩阵:

从以上可以看出,md(x1)划分到D1的代价最小,没有出现决策冲突,也就是不存在决策冗余。
从计算复杂度本文方法与文献[17]方法比较如下:
计算复杂度比较:在不考虑代价矩阵存储缩减情况下,t表示决策类个数,本文的代价矩阵中的阶数个数为t×(t+1),而文献[17]方法定义的代价矩阵阶数个数为t×3t。本文风险矩阵的阶数由8×9阶,降低为8×4阶。
由此,对于协调覆盖决策系统而言,基于三支决策角度来探讨多类分类模型具有实际意义。我们通过一个实例与其他算法比较,说明基于三支决策的协调覆盖决策系统的多类分类模型算法相对更易理解、效率更高。也为协调覆盖决策系统基于三支决策理论思想提供了新的框架。
5 结语
这篇文章讨论了协调覆盖决策系统的多类分类视角下三支决策矩阵模型。我们基于文献[12~13]定义的隶属度矩阵、代价矩阵、风险矩阵的概念,提出了基于协调覆盖决策系统的三支决策多类分类模型计算方法,减少了代价参数,降低了决策风险。本文的研究对于三支决策模型的进一步应用讨论提供一种新的思路,故我们所做工作还是有意义的。在接下来的工作中,需要进一步探讨该模型的性质及定理,以及其对应的属性约简方法等。

