DSNNs: learning transfer from deep neural networks to spiking neural networks ①
Zhang Lei(张 磊) , Du Zidong, Li Ling, Chen Yunji
(*State Key Laboratory of Computer Architecture, Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, P.R.China) (**Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, P.R.China) (***Cambricon Tech. Ltd, Beijing 100010, P.R.China) (****Institute of Software, Chinese Academy of Sciences, Beijing 100190, P.R.China)
Abstract
Key words: deep leaning, spiking neural network (SNN), convert method, spatially folded network
0 Introduction
Deep neural networks (DNNs) perform the state-of-the-art results on many tasks, such as image recognition[1-4], speech recognition[5-7]and natural language processing[8,9]. Current state-of-the-art DNNs usually contain many layers with high abstracted neuron models, causing a heavy burden for computation. To highly efficiently process DNNs, many customized architectures have been proposed.
Despite DNNs, another type of neural network from neuroscience is also emerging. Spiking neural networks (SNNs) mimic the biological brain bionically and consequentially are thought as the next generation of neural networks[10,11]. Spike, used in SNNs to pass information among neurons, is thought to be a more efficient hardware solution as 1-bit is enough for representing one spike. Some special hardware architectures have been proposed for SNNs[12-14]. However, currently, the bio-inspired, spike-based neuromorphic SNNs still fail to achieve comparable results with DNN.
To close the performance gap between DNNs and SNNs, researchers have tried many solutions. IBM[15]proved that the structural and operational differences between neuromorphic computing and deep learning are not fundamental. ConvNets[16]applied a weights converting technique and IBM adopted back propagation (BP) in training. However, these techniques are only proven feasible using small networks on simple tasks, such as recognition on hand-written digital numbers (MNIST[17]). As a result, the capability of SNNs remains unclear, especially on large and complex tasks.
This work proposes a simple but effect way to construct deep spiking neural networks (DSNNs) by transferring the learned ability of DNNs to SNNs. During the process, initial trained synaptic weights are converted and used in SNNs; features in SNNs are introduced to original DNN for further training. Evaluated with large and complex datasets (including ImageNet[18]), DSNNs achieve comparable accuracy with DNNs. Furthermore, to appeal the hardware design, this work proposes an enhanced SNN computing algorithm, called ‘DSNN-fold’, which also improves the accuracy of the directly converted SNN.
Therefore the overall contribution is as follows:
(1) An algorithm to convert DNN to SNN is proposed.
(2) The algorithm is improved for more hardware friendly design.
1 DNN vs. SNN
In this section, two different models are briefly introduced : DNNs and SNNs,as depicted in Fig.1. Despite the layer based architecture, SNNs are different from DNNs in neuron model,input stimuli, results readout and training method.

Fig.1 DNN vs. SNN
1.1 Topology
Both DNNs and SNNs mimic the biological brain but in different levels of abstraction. DNNs usually contain multiple layers where each layer contains numerous neurons; inputs are passed and processed through layers with different inter-layer connections (i.e., synapses) (Fig.1(a)). Recent development of deep learning leads to increasingly deeper and larger networks, i.e., more layers and more neurons in a layer. Meanwhile, connections among layers vary through different types of layers, which consequently leads to different types of layers and neural networks, e.g., multiple layer perceptron (MLP), convolutional neural network (CNN), recurrent neural network (RNN), and long-short-term-memory (LSTM).
Similarly, SNNs consist of multiple layers, but less types than DNNs. Commonly, each neuron connects to not only all neurons in the last layer but also all other neurons in the current layer through an inhibition mechanism. Therefore, the state of each neuron is related to inputs (i.e., spikes) from previous layers and inhibition signals from its layer (Fig.1(b)). The inhibition mechanism, observed from biological nerve system, causes the so-called ‘Winner-Take-All’ effect, i.e., only one neuron can fire in a shot period (inhibition period), which has been proven to achieve good results in previous work[19].
1.2 Neuron model
A typical neuron in DNNs receives different inputs and generates output passing through synapses to following neurons, as shown in Fig.1(c). Formally, a neuron generates outputNoutasNout=f(∑cg(Ii,Wij)), whereIiis the inputs,Wijis the synapse weight,Cis the set of connected input neurons,g() andf() are processing operators.g() can be inner production as in fully-connected layers and convolutional layers, or unsampling in pooling layers.f() is the activation function, such as sigmoid and ReLU functions typically.
A neuron in SNN accumulates input spikes continuously to its potential and fires out spikes to following neurons once its potential reaches the firing threshold; its potential will be reset afterwards. Formally, the potential of an output neuronPout(t) in the time window [T1,T2] can be described by

1.3 Input stimulus
Typical inputs, i.e., image pixels, audio information, are used directly with or without preprocessing like normalization and centralization. Texts are processed to digital representations through word embedding process, such as word2vec[20].
Unlike DNNs, SNNs take spikes as inputs, thus an encoding process which converts numeric values into spikes is required. However, SNN encoding has been a quite controversial topic in the field of neuromorphic computing. There have been years of debates and discussions about better encoding schemes, e.g., rate coding, rank order coding, temporal coding, etc. Despite that, there is no obvious experimental evidence showing the superiority of temporal coding, which uses the precise time of firing —— it is believed that temporal coding carries more information but currently it is unclear how to leverage that. While all of them have been shown to be biologically plausible, researches have proved that SNN with temporal coding schemes is less accurate than rate coding schemes[13], with regard to hardware brevity. Here,rate coding is chosen as the coding scheme in the following sections.
1.4 Readout
The output layer of DNNs is used to classify or recognize the input sample. For example, each output neuron in an MLP corresponds to a label; for CNNs, the softmax function is applied to output layers to turn the output value into probability distributions. Usually, the winner neuron has the maximum output value and will label the input with its label.
Readout in SNN is tightly related to the network topology and training method. All these different readouts aim to find the winner output neuron(s) as DNNs. The winner neuron can be the one having the largest potential, the one firing first or the one firing most times. Note that output neurons in SNNs could be much more than the labels[13]. Thus the current input sample can be labeled with the label of the winner neuron or neurons. In this work, considering the construction work from DNNs to SNNs, which is trained with supervised learning, 3 readout strategies are exploited that might fit in the transferred networks, i.e., FS (first spike), MS (maximum spike times) and MP (maximum accumulated potential). In this exploration, FS fails to achieve the same accurate results with other two strategies; while MS and MP show good performance on simple tasks such as MINIST or simple networks such as Lenet-5. However, MS fails on larger or deeper topology where the accuracy drops drastically. Therefore, MP readout method is the first choice which shows steady good performance.
1.5 Training
Training is essential and crucial to DNNs and several training methods have been proposed. Among them, BP, a supervised learning algorithm, has been proven to be most effective. During neural network training, errors between actual outputs and desired outputs are back propagated to input layers to adjust the network parameters gradually.
SNN training techniques are far different from DNNs. Most SNNs adopt neuromorphic learning models in biology/neuroscience to optimize their training processes. For example, the well-known STDP (spike-timing-dependent plasticity) mechanism, an unsupervised learning algorithm, achieves similar accuracy as a two-layer MLP on MNIST dataset[21]. In STDP, the learning principle is to detect causality between input and output spikes (i.e., presynaptic and postsynaptic). If a neuron fires soon after receiving an input spike from a given synapse, it suggests that synapse plays an important role in the firing, and thus it should be reinforced by long-term potentiation (LTP). Conversely, if a neuron fires a long time after receiving an input spike, or shortly before receiving it, the corresponding synapse will be depressed by long-term depression (LTD). Additionally, neuron will adjust its potential threshold to keep the neuron firing at a reasonable speed through a homeostasis mechanism. Thus, all the neurons are forced to participate with similar activities. Recently, researchers begin to explore supervised learning with backward propagation. But none of them is able to achieve the comparable results as BP in DNNs, especially on tasks with larger problem sizes.
2 Constructing DSNN
In this section, a construction procedure that transfers learned ability in DNNs to SNNs is proposed. This work focuses on CNNs. As shown in Fig.2, the DSNN construction workflow can be divided into 2 stages: from CNN to SNN and from SNN to CNN. In the former stage, DSNN is constructed with weights and topology directly converted from CNN; in the latter stage, SNN features are introduced in the original CNN which will be modified for further training. Final DSNN is constructed with retrained weights.

Fig.2 Flow of DSNN construction
2.1 Intrinsic consistency between DNNs and SNNs
The intrinsic consistency between DNNs and SNNs reveals a possibility of transferring the learned ability of DNNs to SNNs. Despite the differences of neuron models and training algorithms, regarding the inference, DNNs can be viewed as a simplified version SNNs by removing the timing information. Given an SNN and a DNN in a same topology, considering the formulas in Section 1, SNN turns out to convert the original input of the DNN from floating-point numbers or high fixed-width numbers into lower width integers of spikes if removing the time window. The following question is about the accuracy loss due to that conversion. Previous work show that spiking encoding currently works worse. However, recent work on less bit-width for data representation have been extended to binary neural networks[22-24]that use 1 bit for data. Such feature indicates that SNNs with rate encoding may not suffer accuracy loss due to moderate discretization of DNNs inputs.
In addition, ReLU, the most popular activation function used in deep learning[25,26], may help to bridge the gap between DNNs and SNNs. ReLU eliminates the negative neuron outputs and preserves the linear property of the positive outputs. Its function is intrinsically consistent with the firing mechanism (IF model) in SNN that a neuron fires only when its potential (always≥0) is larger than the threshold. That indicates that an integrate-and-fire (IF) neuron[27]is equal to an ‘artificial neurons plus ReLU’ in some degree.
2.2 From CNN to SNN
TopologyTo transfer the learned ability, multiple layers are needed in SNN to achieve the functions of different layers in CNN. Intuitively and directly, this work constructs a new topology of SNN with SNN-CONV, SNN-POOL, and SNN-FC layers for convolutional (CONV), pooling (POOL), and fully-connected (FC) layers, as shown in Fig.3. In another words, SNN retains the connections and weights in the trained CNN during the transfer. Especially, for layers having no weights like POOL, SNN-POOL is constructed with fixed weights 1/Size(Kernel), whereSize(Kernel)is the number of presynaptic neurons in the kernel.
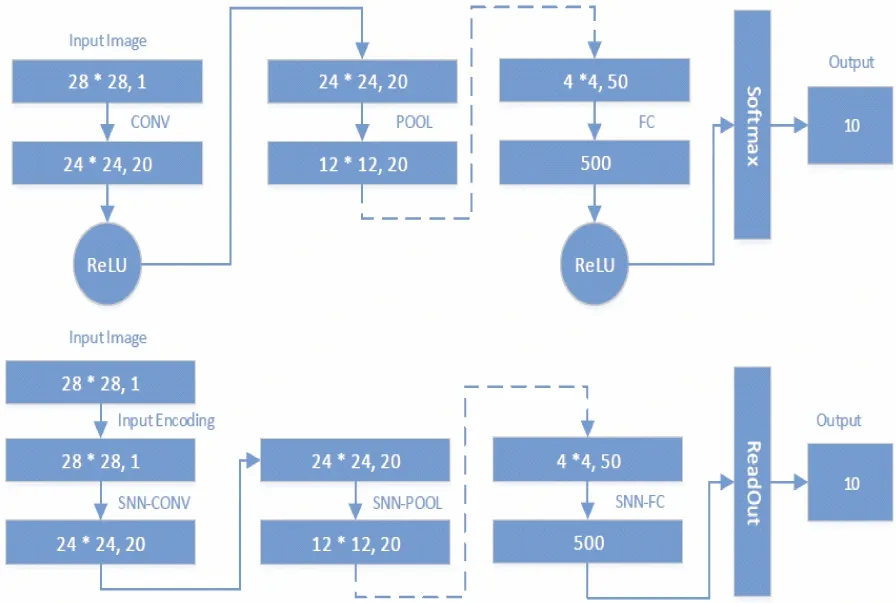
Fig.3 DSNN construction from LeNet-5
InputThis work has explored 2 commonly used methods uniform coding[12]and Poisson coding[28]to encode CNN input values into spike trains for SNN. With uniform coding, the input neuron fires periodically with a firing rate which is proportional to the input value. With Poisson coding, the input neuron fires spikes following a Poisson process whose time constant is inversely proportional to the input value. Additionally, note that the centralization and normalization techniques in DNNs can accelerate the convergence of the training process, but it will inevitably introduce negative input values. To overcome the difficulty that input spikes are unable to decrease the neuron potentials, ‘negative spike’ is introduced in the converted SNN model.
For an input neuron firing a ‘negative spike’, received neurons integrate it similarly as positive spikes but decrease their potentials.
ParametersThe converted SNN needs to decide 2 types of parameters: synapse weights and firing threshold in each neuron. For the former one,they are directly obtained from the fully trained CNN in the from SNN to CNN flow.
For the latter one, previous methods such as model-based normalization and data-based normalization[16], work only on simple and small datasets/networks, such as MNIST/LeNet-5, but fail on larger datasets and complex networks, such as ImageNet/AlexNet. The model-based method requires large spike time window and leads to longer computation latency in SNN. Data-based method is worse, since it needs to propagate the entire network with the entire training data set and store all the activations which will further be calculated as scaling factors.Instead, this work proposes a greedy search based method to decide the firing thresholds, as shown in Algorithm 1, which makes better trade-offs between accuracy and efficiency.Briefly, first find the maximum possible outputMifor each layer based on the current weight model (in Algorithm 1,Mi=input_sum,input_wtis the synapse weight). The threshold for each layer is given byσ×Mi, whereσis a constant to be decided. Search widely onσin the set {1, 0.1, 0.01,…} until a satisfactory result is obtained. To guarantee the optimal thresholds, greedy search on the nearby thresholds is needed.

Algorithm 1: Threshold set algorithmfor layer in layers do maxposinput = 0 for neuron in layer. neurons do inputsum=0 for inputwt in neuron.inputwts do inputsum+=max(0, inputwt) end for maxposinput = max(maxposinput, inputsum) end for layer.threshold=σ×maxposinput.end forSearch on σ in the set {1, 0.1,0.01, …} until a satis-factory result is obtained.
2.3 From SNN to DNN
After the first stage of transfer, features from the converted SNN are introduced to the original CNN model for further adjustments. The adjusted CNN will be trained finely to obtain parameters that better retain the accuracy on SNN.
ReLUactivationsIn CNN, all the CONV layers and FC layers are made to use ReLU as an activation function, in order to eliminate negative neuron outputs (which could be only transferred as ‘negative spikes’ in SNN). There is no need to add ReLU functions after POOL layers since both MAX-POOL and Average-POOL do not change the polarity of input spikes. Fortunately, most of the mainstream CNNs have already included ReLU as activation function since it is shown to have better accuracy results.
AveragepoolingRegarding the pooling layer in CNN, this work changes them to average pooling (AVG-POOL) as it is easier to be simulated in the form of spikes. Also, previous work have demonstrated that MAX-POOL or AVG-POOL does not have a significant impact on network accuracy[29].
BiasNo suitable methods have been found to accurately simulate bias in SNN.
The adjusted CNN in this stage will be fully trained to obtain new weights. Together with the SNN architecture in the first stage, a powerful DSNN is constructed.
The performance of the DSNNs is reported in Section 4.
3 Spatially folded DSNN
Considering the contradiction of limited hardware resources and unlimited size of networks, architects have to design architecture flexible enough to be reused in time, i.e., a time division multiple accesses method. In another words, algorithms should compute different pieces at different time. Specifically, network should be folded spatially. For time-independent CNNs, they can be divided easily for a small footprint of hardware[30]. However, this spatially-foled property will not hold in any previous SNNs including the DSNNs, because the computation in each neuron is strongly related to the firing time of each pre-synaptic neuron. To solve this problem, previously proposed architectures usually use an expanded method for the computation which keeps the time causality.
This work proposes an algorithm to further construct ‘DSNN-fold’ for hardware benefit while maintaining the accuracy results.The key feature of ‘DSNN-fold’ is the split two-phase computation, which is described in Fig.4 and Fig.5. In first phase, postsynaptic neurons accumulate their potentials if the corresponding presyanptic neuron emits negative spikes. Since negative spikes only reduce the neuron potentials, postsynaptic neurons will not fire spikes. In the second phase, positive spikes are fired to postsynaptic neurons. Other parts such as input encoding, readout and threshold policy are not changed. Obviously, the 2 phases are independent and will not affect the number of spikes. Thus, in DSNN-fold, the computation can be divided into pieces.
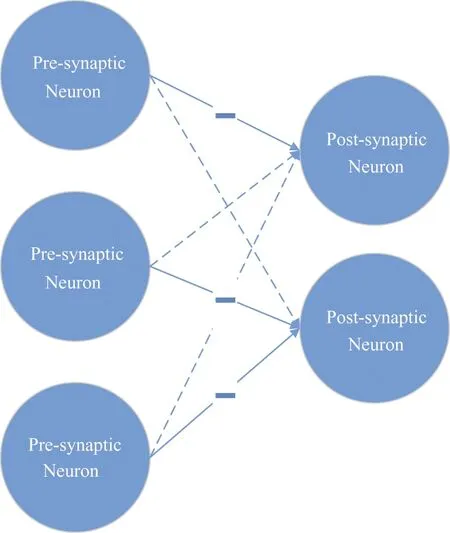
Fig.4 The first phase of DSNN-fold

Fig.5 The second phase of DSNN-fold
By using the DSNN-fold method, the spatio-temporal correlation of the entire SNN is removed. In this way, the deployment of network segments of any size can be realized in hardware mapping. As shown in Fig.6, the computation of an SNN network is split into operations of independent layers. The operation of each layer can be divided into 2 phases and the polarity of the influence of the operations in each phase on the output neurons is independent and stable. Therefore, it is possible to split computations in each phase into several fragments. Computations in each fragment will be easily mapped to any hardware design.
Fig.6 Folded SNN
Interestingly, the accuracy results of DSNNs-fold are actually slightly higher than DSNNs. That is mainly because DSNNs-fold eliminates the disturbance of accidental spiking due to randomly input spikes from the previous layer.
Also, the firing thresholds determination is much easier. In DSNNs, the threshold is sensitive as the neuron will fire too much times than the expected if positive spikes come first. However, in DSNNs-fold, the final numbers of spikes depend on inputs, regardless of the coming order.
Additionally, maximum pooling is feasible in DSNNs-fold either, as it could be achieved by selecting the neurons with maximum number of spikes and inhibiting other neurons to propagate to the next layer.
4 Evaluation
4.1 Methodology
In this work, 4 representative CNNs are selected as benchmarks, and implement those 4 CNN models with Caffe[31], including LeNet-5[17], caffe-cifar10-quick[2], AlexNet[1]and VGG-16[3], as shown in Table 1. The
4 CNNs are designed for 3 different datasets: LeNet-5 for MNIST, caffe-cifar10-quick for CIFAR10, AlexNet and VGG-16 for ImageNet. Particularly, MNIST consists of 60 000 individual images (28×28 grayscale) of handwritten digits (0-9) for training and 10 000 digits for testing. CIFAR-10 consists of 60 k colorful images (32×32) in 10 classes. ImageNet ILSVRC-2012 includes high resolution(224×224) images in 1 000 classes and is split into 3 sets: training (1.3 M images), validation (50 k images), and testing (100 k images).
The classification performance is evaluated using 2 measures: the top-1 error and top-5 error. The former reflects the error rate of the classification and the latter is often used as the criterion for final evaluation.

Table 1 Network depth comparison
4.2 Accuracy
Table 2 compares the accuracies achieved by CNN, adjusted CNN (adjustments in stage from SNN to CNN), DSNN, and DSNN-fold. Adjusted CNN causes trivial accuracy loss (0.01% to 2.42%) compared to CNN. Even for the deepest network, VGG-16, the accuracy loss is only 2.42%. This illustrates that CNN training is able to make trade-offs on strategies like bias and max-pooling, if the only factor that is taken into consideration is accuracy, and other factors such as convergence speed are ignored in such cases.
For small networks on MNIST and Cifar datasets, DSNN-fold achieves comparable results with adjusted-CNN, with accuracy decreases of 0.1% and 0.56% respectively. Moreover, for large scale networks, AlexNet and VGG-16, the top-1 and top-5 errors are restricted to a reasonable range (i.e., 1.03% and 1.838% for AlexNet, 3.42% and 2.09% for VGG-16). Compared to previous work of converting CNN to SNN, the results greatly improve the accuracy achieved by SNN.
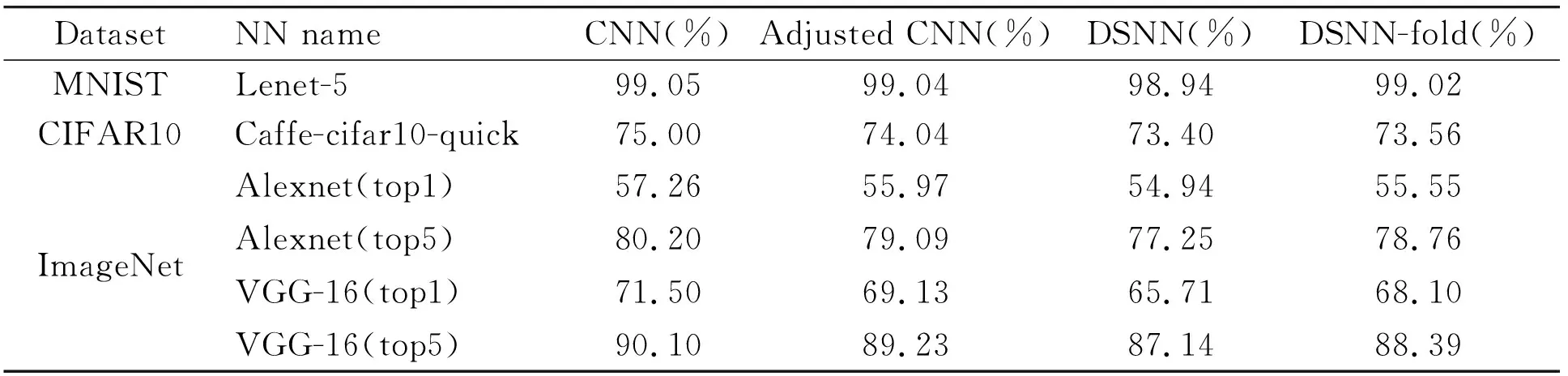
Table 2 Accuracy results
As the number of network layers increases, the accuracy loss of SNN slowly increases due to parameter settings. Two of the key parameters are the image presentation time and the maximum spike frequency. Consistent with the original SNN, the maximum firing frequency is limited no larger than 100 Hz and the image presentation less than 500 ms in this work. SNN could be more efficient in practical tasks under these parameters. However, these limitations could lead to bad simulation of output behaviors of CNN neurons. This problem has been solved by applying the following DSNN-fold algorithm. Another crucial parameter is the firing threshold. In order to reduce the complexity of SNN, the same threshold value is set to neurons in the same layer despite they can be set independently. Although the simplified threshold setting strategy is able to reduce the workloads of threshold setting, this work sacrifices the higher accuracy that could be obtained by setting an independent threshold for each neuron.
Compared to DSNN, DSNN-fold achieves a better accuracy, e.g., 88.39% for VGG-16, which is slightly higher than the accuracy achieved by DSNN. In original SNN, the positive and negative spike timings cross each other, and bring about unreasonable firing behaviors of postsynaptic neurons. However, in DSNN-fold, such behaviors avoided as negative spikes are computed before positive spikes.
The pre- and post-conversion accuracy and accuracy of previous SNN on a typical network are presented in Fig.7. From left to right, the complexity of the network is gradually increasing, and the difficulty of identifying tasks is also gradually increasing. Although the performance of DNN, SNN and the proposed method is very similar in the simple task, the stability of our method is obviously better than that of the previous SNN network. Obviously, on the performance of complex tasks, the improvement of the proposed method compared to the previous SNN algorithm is significant. Considering that the best result of previous SNN work on ImageNet was 51.8%(top1) and 81.63%(top5)[32,33], this work improves the accuracy of the SNN on ImageNet by a maximum of 6.76%. It is clear that our SNN is able to achieve practical results on complex recognition tasks.

Fig.7 Compare accuracy results among typical networks
4.3 Maximum spikes vs. maximum potential
This work selects the maximum potential (MP) strategy over the maximum spikes (MS) strategy as the readout strategy due to its ability to support large scale networks. These 2 strategies are evaluated on benchmarks shown in Fig.8. These 2 strategies achieve similar performance on small datasets and networks. However, on large datasets and networks, the performance of MS strategy is poor, as many neurons in the last layer produce the same number of maximum spikes, which seriously blocks the judgement of output labeling in MS.
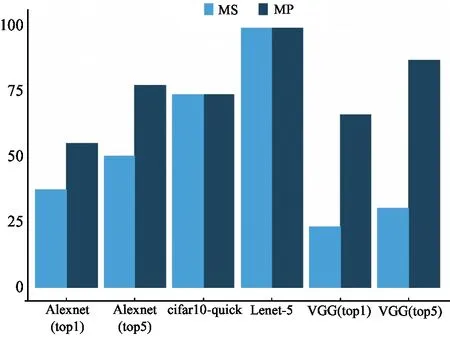
Fig.8 Comparison between 2 readout strategies
4.4 Robustness
The performance of the 2 encoding methods mentioned in Section 1 are compared in Fig.9. Both methods achieve satisfactory performance in the conversion methods. Poisson coding adds randomness to the input stimulus which proves that the converted SNN can still be effective under unstable input environment. Since Poisson encoding is statistically random and will increase the computational complexity, it is not recommended to be applied in algorithms or hardware designs.

Fig.9 Comparison between 2 coding schemes
5 Discussion
Compared to traditional CNNs, the major advantage of DSNN is that it will significantly reduce hardware storage and computation overhead.On the one hand, DSNN converts floating-point numbers with large data width into fixed-point spikes with smaller data width,thereby reducing storage overhead. On the other hand, DSNN divides the dot product operation in CNN into add operations, which will significantly reduce the computational power consumption and area in the hardware.
Compared with another similar network BNN (binary neural network)[23], the effect of SNN on reducing overhead is obviously inferior to it, because BNN only operates 1 bit neurons and weights. Besides, one add operation is needed for calculating the effect of one input neuron on an output neuron. Although DSNN is weaker than BNN in this respect, DSNN achieves better accuracy compared with BNN. Note that BNN has completely failed to complete the task on ImageNet.In summary, DSNN is very suitable for working in high-precision and low-cost work scenarios.
The practice of using ReLU activations to avoid negative neurons has appeared in many articles, but it still lacks reasonable interpretations of the occurrence of negative weights. It is a generally accepted fact that it takes much more SNN neurons with inhibitory mechanisms to simulate negative weights, therefore the conversion techniques of turning CNN into a biological SNN is still worth exploring. If SNN would one day be considered in hardware design, the quantification of weights and neuron potentials are also critical, which requires the SNN to remain high precision with low-precision weights like half-precision floating-point weights or neuron potentials. The latest CNN technologies such as sparse and binary techniques also pose challenges to the accuracy of the SNN, and it remains unknown whether SNN can successfully transform them.
In addition to the previous classic network algorithms, combined with the latest generative model, DNN is still making breakthroughs in multiple application scenarios[33-36]. How SNN completes new network technologies such as GAN in DNN is still worth studying.
6 Conclusion
This work proposes an effective way to construct deep spiking neural networks with ‘learning transfer’ from DNNs, which makes it possible to construct a high precision SNN without complicated training procedures. This kind of SNN has been able to match the accuracy of CNN in complex mission scenarios, which is a huge improvement over the previous SNN. This work also improves the computing algorithms of the transferred SNN in order to extend SNN to a spatially-folded version (DSNN-fold). The DSNN-fold turns out to be effective in both accuracy and computation, which can be a good reference for future hardware designs.
 High Technology Letters2020年2期
High Technology Letters2020年2期
- High Technology Letters的其它文章
- Attitude estimation method based on extended Kalman filter algorithm with 22 dimensional state vector for low-cost agricultural UAV ①
- Contract theory based incentive mechanism design for buffer resource in wireless caching networks ①
- NNL: a domain-specific language for neural networks ①
- Research on optimization design method of actuator parameters with stepless capacity control system for reciprocating compressor ①
- Active micro-vibration control based on improved variable step size LMS algorithm ①
- RGB and LBP-texture deep nonlinearly fusion features for fabric retrieval ①
