基于EPANET的再生水滴灌系统余氯分布模型构建
王 珍,郝锋珍,2,李久生,栗岩峰
基于EPANET的再生水滴灌系统余氯分布模型构建
王 珍1,郝锋珍1,2,李久生1※,栗岩峰1
(1. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京 100048;2. 山西农业大学城乡建设学院,太谷 030801)
加氯处理是保证滴灌系统安全的重要措施之一,但是氯与灌溉水及滴灌管壁发生反应而引起的衰减会对余氯分布均匀性造成不利影响。该研究采用EPANET软件构建了再生水滴灌系统水力性能及余氯运移、衰减和分布模型,基于试验数据对模型水力和水质模拟参数进行率定和验证,并应用该模型分析了加氯模式(浓度-时长:1.3 mg/L-185 min、3 mg/L-80 min、6 mg/L-40 min和8 mg/L-30 min)和毛管长度(10~150 m)对系统余氯分布特征的影响。结果表明,EPANET软件可以较好地模拟滴灌系统水力性能及余氯分布特征,沿毛管方向余氯浓度模拟值与实测值一致性指数达到0.75以上。当毛管长度由10 m增加至150 m时,灌水单元平均余氯浓度与毛管末端余氯浓度随毛管长度增加呈先升高而后降低趋势,高浓度加氯处理平均余氯浓度和毛管末端余氯浓度随毛管长度增加衰减速率相对较小。较短的加氯历时(< 40 min)和过低的加氯浓度(如1.3 mg/L)均易造成余氯质量偏差率升高和均匀系数降低;建议使用加氯浓度3 mg/L且加氯时长80 min的加氯模式,该模式毛管极限铺设长度达到66 m,余氯质量均匀系数超过90%。
氯;模拟;水力性能;水质;滴灌;EPANET
0 引 言
灌水器的堵塞防止和处理一直是再生水滴灌系统安全运行的核心问题[1]。通过向再生水滴灌系统加氯,可以有效抑制微生物生长,减缓灌水器堵塞形成[2]。Ravina等[3]研究指出余氯浓度控制在3~5 mg/L时可有效控制灌水器堵塞;Cararo等[4]则指出控制余氯浓度为0.5 mg/L对于控制灌水器堵塞更为有效;Li等[5-6]发现低浓度、长历时的加氯模式更有利于减轻系统堵塞的发生。但是,因氯具有强氧化性,其在缓解灌水器堵塞的同时可能会对土壤环境及作物根系产生不利影响[7]。再生水滴灌适宜加氯模式的制定需综合考虑加氯对系统性能和作物生长的共同影响[8-9]。Li等[8]发现控制余氯浓度为2~8 mg/L、加氯间隔为4~8周既能控制系统堵塞,又不会对番茄生长、产量和品质产生明显影响;Hao等[9]发现加氯一定程度上抑制了土壤酶活性,较低的余氯浓度不会对玉米生长造成影响。上述研究为再生水滴灌系统加氯模式优化提供了重要理论基础。但是,加氯过程中余氯浓度会随氯与灌溉水及管壁发生反应而衰减[10],在灌水器流量不均匀性的叠加作用下,滴灌系统中可能出现部分灌水器加氯过量或加氯不足的情况,导致部分区域土壤环境恶化而部分区域堵塞控制效果不佳。定量研究再生水滴灌系统中余氯分布特征及其影响因素对进一步优化加氯模式具有重要意义。
通过水力解析(如能量轮廓线法)或数值计算方法(如有限元法)对管网水力特性进行计算,并对灌水均匀性进行评价,是滴灌系统管网优化的基础[11-13]。但是,以往滴灌系统水力特性计算方法中较少考虑溶质迁移转化过程及其在灌溉系统的运移分布特征,一定程度上限制了溶质(如肥料和氯)注入模式对系统性能的影响研究。近年来,基于EPANET构建的城镇供水管网余氯分布模拟模型已在模拟不同管网布置形式、供水方式和加氯模式条件下余氯分布特征中得到广泛应用[10,14-15]。与城镇供水管网相比,滴灌系统出流节点(灌水器)更多,且节点流量受水力偏差影响明显,相对较低的滴灌系统管网平均流速(约0.3 m/s)可能加大氯或肥料自加注点运移至不同位置灌水器的时间差异[16],能否基于EPANET软件实现滴灌系统中余氯浓度和肥料分布的模拟是一个值得关注的问题。本研究基于EPANET在供水管网水力和水质模拟中的优势,建立再生水滴灌系统余氯分布模型,并基于该模型评价滴灌系统参数及加氯模式对余氯分布特征的影响,以期为再生水灌溉条件下的系统设计及加氯模式优选提供科学依据。
1 模型构建及试验方法
EPANET是美国环境保护署(Environmental Protection Agency,EPA)开发的有压管网水力和水质特性延时模拟软件,可实现不同类型的供水系统水力及水质特性分析[17],已在余氯衰减运移中得到了大量应用。
1.1 再生水滴灌加氯系统模型构建
基于EPANET软件,本研究构建了滴灌系统典型灌水单元,包括水源1处、干管1根、支管1根、毛管若干条及灌水器若干个(图1)。滴灌系统毛管数量、单条毛管上灌水器水量、毛管间距、灌水器间距和灌水器流量等技术参数可根据系统实际情况取值。本研究假定加氯点位于水源处,加入的氯通过干管—支管—毛管—灌水器后滴入土壤。
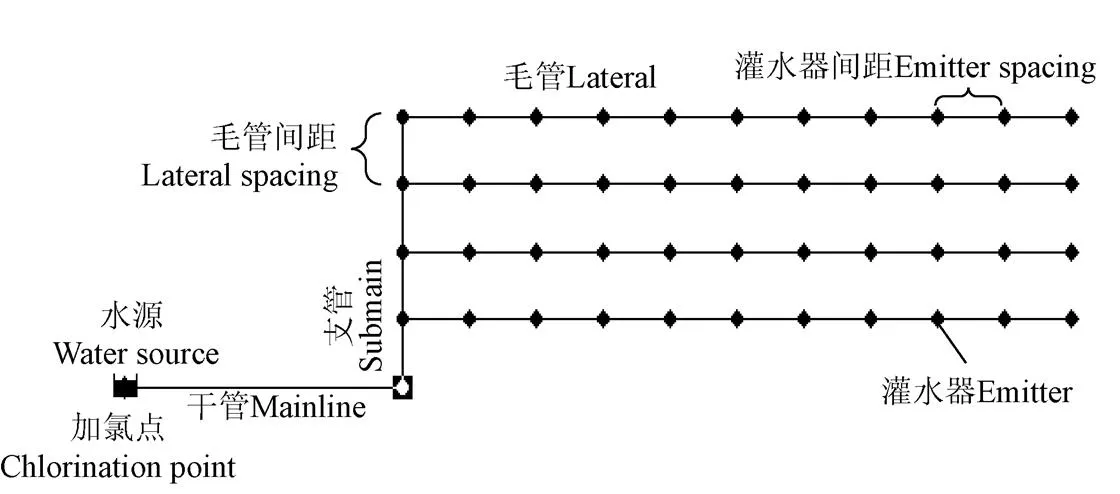
图1 滴灌加氯系统组成示意图
1.1.1 水力模拟
管网水力计算分析包括管网节点流量连续方程和管段能量方程的联立求解。节点流量连续方程如式(1)所示:
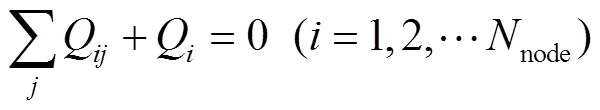
式中Q为与节点相连的管段的流量,L/h;Q为节点流量,L/h;为节点编号;node为节点数量。管段能量方程如式(2)所示:

式中H和H分别为节点和处的水头,m;h为管段水头损失,m;为阻力系数;为流量指数。本研究中采用Hazen-Williams公式求解管段的水头损失。EPANET采用Todini-Pilati梯度算法求解给定时间点管网水力状态的流量连续性方程和水头损失方程组[18]。滴灌系统水力性能模拟时,灌水器节点类型设置成“Emitters”,其节点出水量与节点压力关系如式(3)所示:
=KP(3)
式中为灌水器实际流量,L/h;为流量系数;P为压力水头,m;为灌水器流态指数。
滴灌系统水力模拟时,所需的水力参数主要包括水源工作压力、干管、支管和毛管阻力系数(R、R和R)、灌水器流量系数和流态指数及节点初始流量(Q,L/h)。其中,工作压力可根据实际情况进行设置;灌水器流态指数和流量系数可由实测的压力-流量关系曲线拟合得到;阻力系数根据管道材质设置初始值,并经实测的滴灌系统灌水器流量进行率定。
1.1.2 水质模拟
针对构建的滴灌系统,加氯条件下管网水质模拟的主要任务是在管网水力计算的基础上,基于管网中溶质对流传输规律,预测余氯(水经过加氯消毒接触一定时间后,水中所余留的以游离氯、化合氯或两者并存形式存在的氯)[19]在管网内的时空变化。有效氯的传输衰减过程包括管道内物质的对流传输过程、物质动态反应过程及节点混合引起的物质浓度变化。管道内物质的对流传输方程见式(4)[17]:

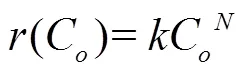
式中C为管道中的余氯浓度,mg/L;u为管道中的流速,m/h;(C)为管道中反应物的反应速率,对于非反应物,(C)=0,mg/(L·h);为总余氯衰减系数,1/h;为反应级数;为管道编号;pipe为管道数量。。
本研究忽略加入氯在水源中的混合过程,假设水源处的加氯浓度(有效氯,以Cl计,下同)[20]恒定,进而通过给定水源处加氯浓度的方式对余氯分布进行模拟。采用一级氯衰减模型来模拟滴灌系统内的余氯衰减,则=1。本研究中设定滴灌系统干管、支管和毛管采用PVC或PE管材,可忽略管壁腐蚀引起的氯衰减。因此,余氯衰减过程主要包括主体水余氯衰减和管壁衰减,二者之和构成管网余氯衰减[21]:
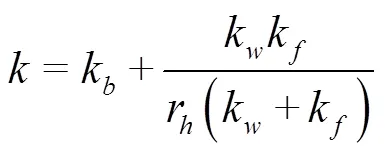
式中k为主体水衰减系数,1/h;k为管壁衰减系数,m/h;r为水力半径,m;k为质量传输系数,模型中根据舍伍德数、管道长度、水力半径、雷诺数等进行计算。
1.2 试验材料与方法
1.2.1 滴灌系统水力性能试验
试验于2017年9月在国家节水灌溉北京工程技术研究中心大兴试验基地进行。在田间构建滴灌系统1套,滴灌系统包括:水源1处(4 m×4 m×2.5 m水池),用于提供灌溉用的二级处理再生水;邻近水源处设置比例泵1台(Mis Rite Model 2504,Tefen,以色列),用于向系统中注入有效氯溶液,使系统加氯浓度与设计值一致;精密压力表1个(0.4%,0.40 MPa),用于测定干管首端工作压力;干管(50 mm PVC管)1条,长度25 m,内径46 mm;干管末端设置支管(40 mm PVC管)1条,长度36 m,内径36 mm;支管末端设置内镶贴片式滴灌带1条(TYPHOON,16 mm,耐特菲姆),内径15.6 mm,灌水器间距0.3 m,0.1 MPa条件下灌水器标称流量1.6 L/h。试验中,设置滴灌带长度为100和50 m,分别记为滴灌系统A和B。
试验开始前按照ASAE标准(S553)测定灌水器流量-压力关系[22],计算得到灌水器流量系数为0.495,流态指数为0.476。试验中,利用阀门控制干管首部压力为0.1 MPa。沿毛管方向,每隔2个灌水器设置1处灌水器流量监测点,利用水桶承接20 min内灌水器出流,利用量筒测定承接水量,以此计算沿毛管方向灌水器流量。水力性能测试设置3个重复,每个重复测试时,干管和支管不变,对滴灌带进行更换,将3次测定值进行平均得到不同观测点处灌水器流量。
1.2.2 滴灌系统水质测定试验
1)主体水衰减试验
再生水选用二级处理再生水,取自北京市大兴区黄村污水处理厂,水质指标如表1所示。主体水衰减由室内烧杯试验确定。氯原材料选用10%有效氯(有效系数×含氯量)的次氯酸钠,余氯浓度采用便携式余氯计(ExStik CL200,Extech Instruments Corporation,美国)测定。为研究加氯浓度对再生水主体水衰减规律的影响,本研究控制水温为20℃,参考常用加氯浓度[3-5],设置加氯浓度为1.45、2.30、3.98、8.14 mg/L,研究加氯2 h内的氯衰减变化规律,分别于1、3、5、7、9、11、20、30、40、60、90、120 min测定余氯值并记录。
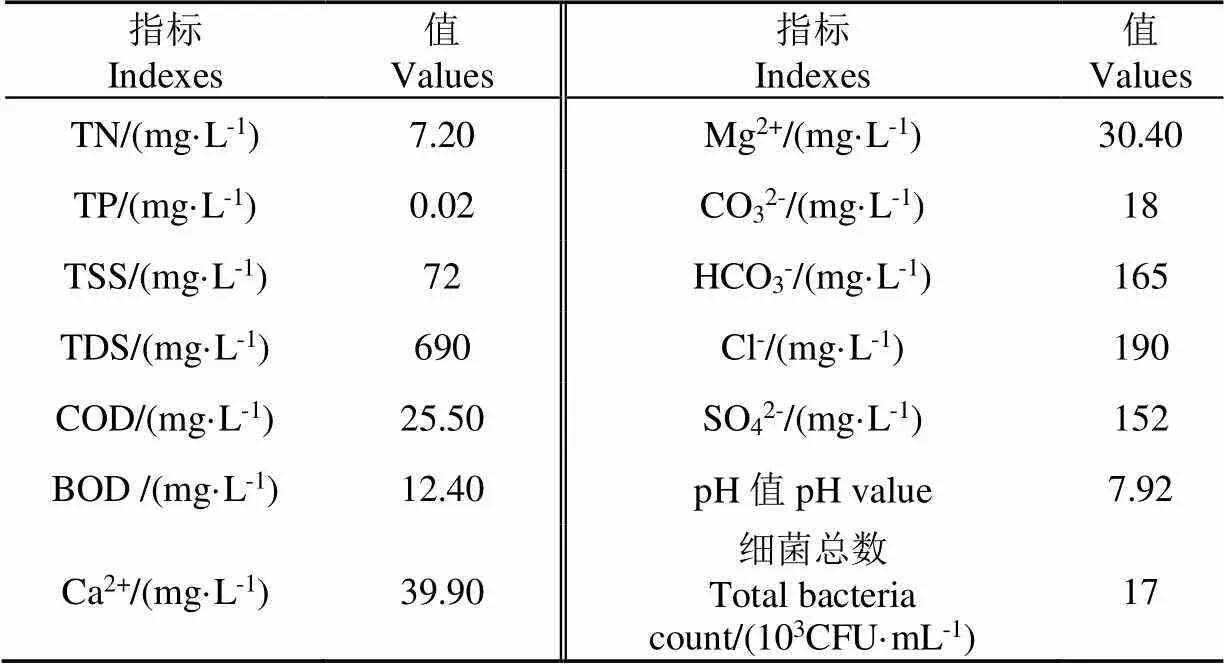
表1 试验用再生水水质指标
2)滴灌系统余氯浓度衰减试验
在系统水力性能试验的基础上,通过比例泵向干管中注入恒定浓度的次氯酸钠溶液,使加氯点有效氯浓度达到设计值。参照主体水衰减试验,设置4个加氯浓度,分别为1.3、3.0、6.0和8.0 mg/L。为保证试验环境温度与主体水衰减试验类似,所有试验均在15:00-18:00进行,试验过程中环境温度范围为20~25 ℃。对于滴灌系统,分别在干管末端和支管末端设置1处水质监测点,沿毛管方向等间距布置10个水质监测点,用以对余氯浓度分布进行测定。对于每组测试,加氯总时长为2 h。自加氯开始至加氯1 h期间,不进行取样;加氯1 h后(假定此时系统不同位置余氯浓度不随时间变化),按远离加氯点方向依次在干管末端、支管末端和毛管上进行灌水器出流采样,立即进行余氯测试(每次采样及余氯测试约耗时4 min),得到各位置余氯浓度。与水力性能试验对应,对于每个加氯浓度也设置3个重复,每个重复中更换滴灌带后进行余氯浓度测试,将3次测定平均值作为监测点处余氯浓度。
1.3 模型评价
本研究中,模型模拟效果评价分水力模拟评价和水质模拟评价两部分组成,分别以灌水器流量及出流液中余氯浓度为对象进行评估,模拟值和观测值的吻合程度采用均方根误差(Root Mean Square Error,RMSE)和一致性指数()进行评价[23]。RMSE最小值为0,越接近0模拟效果越好;值范围为0~1,越接近1模拟效果越好。
2 模型率定与验证结果与分析
2.1 水力参数
模型模拟时,利用系统A灌水器实测流量对参数进行率定,利用系统B灌水器实测流量对率定参数进行验证。经率定和验证,R、R和R分别为100、105和135。表2给出了灌水器流量模拟评价指标。灌水器流量模拟值和实测值平均流量基本一致,系统A、B均方根误差(RMSE)分别为0.026和0.014 L/h,一致性指数()分别为0.88和0.57,模拟值与实测值具有较好的一致性。综上,利用EPANET软件对滴灌系统水力性能能进行模拟具有较高的精度。
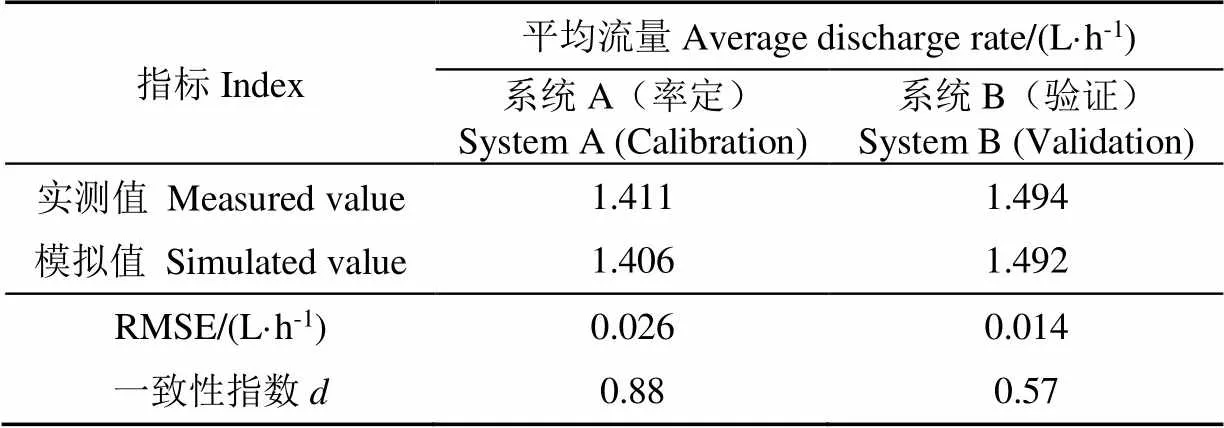
表2 灌水器流量模拟评价
2.2 水质参数
2.2.1 主体水衰减系数计算
不同加氯浓度条件下,再生水主体水衰减规律见图2。不同加氯浓度条件下,余氯浓度衰减曲线的变化规律基本一致。

图2 不同加氯浓度的余氯衰减规律
反应初期,余氯衰减迅速,大约30 min后衰减趋于平缓,这是因为该阶段易于被氧化的有机物和无机物在反应初期占主导,氯的衰减速率快。当易于被氧化的物质消耗之后,不易与氯发生反应物质占主导,导致氯衰减速率相对较低。按照一级动力学式(7)对余氯衰减过程进行拟合[24],得到加氯浓度为1.45、2.30、3.98和8.14 mg/L时的主体水衰减系数分别为0.415、0.301、0.222、0.132 1/h,2分别为0.791、0.750、0.955、0.810。
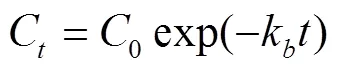
式中C为时刻的余氯浓度,mg/L;0为加氯浓度,mg/L。
利用幂函数拟合主体水衰减系数k与加氯浓度的关系(图3),进而可基于拟合方程计算出系统试验中加氯浓度为1.3、3、6和8 mg/L时,主体水衰减系数分别为0.446、0.257、0.163和0.136 1/h。
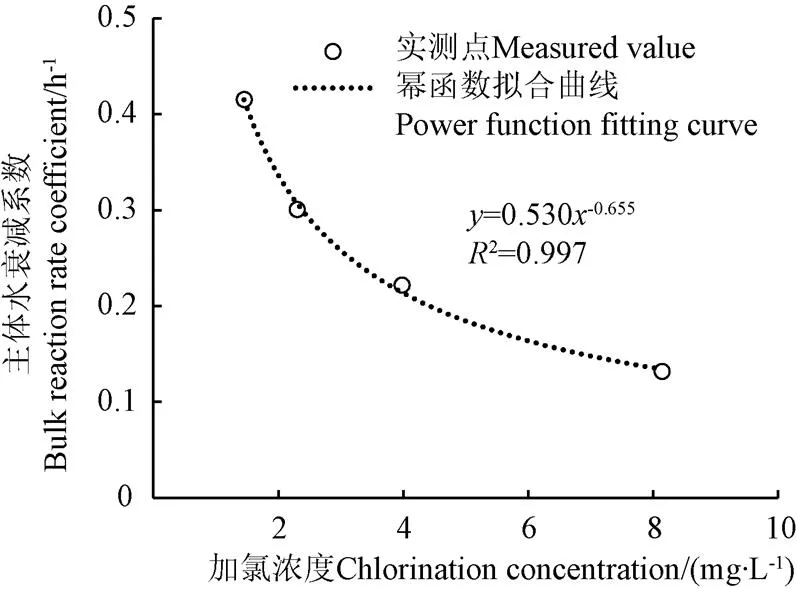
图3 主体水衰减系数与加氯浓度关系
2.2.2 管壁衰减系数率定与验证
参照EPANET技术手册设定干管、支管及滴灌带管壁的初始余氯衰减系数,分别基于系统A和B余氯测定结果对干管、支管和毛管管壁衰减系数(分别为wm、ws和wl)进行率定和验证。图4给出了滴灌系统A不同加氯浓度下的余氯模拟值与实测值比较结果。由图可知,不同加氯浓度条件下,余氯浓度模拟值与实测值吻合程度较好。观测点余氯浓度实测值及模拟值均随距加氯点距离增大呈下降趋势,这说明随水流推进及运移时间增加,灌溉水中氯与灌溉水及管壁发生了明显反应。表3给出了不同加氯浓度条件下余氯分布实测值和模拟值RMSE和。由表可知,参数率定后,不同加氯浓度条件模拟RMSE均相对较小(0.12~0.26 mg/L),余氯浓度实测值与模拟值差异不大;同时,一致性指数()均大于0.75,模型模拟精度较高,这说明使用EPANET软件进行不同规模滴灌系统余氯浓度的模拟是可行的。由表3还可看出,管壁衰减系数基本随加氯浓度的升高而降低,这与Hallam等研究结果一致[21],主要是因为加氯浓度低时,加入氯与灌溉水及管壁的反应比例较高造成的。
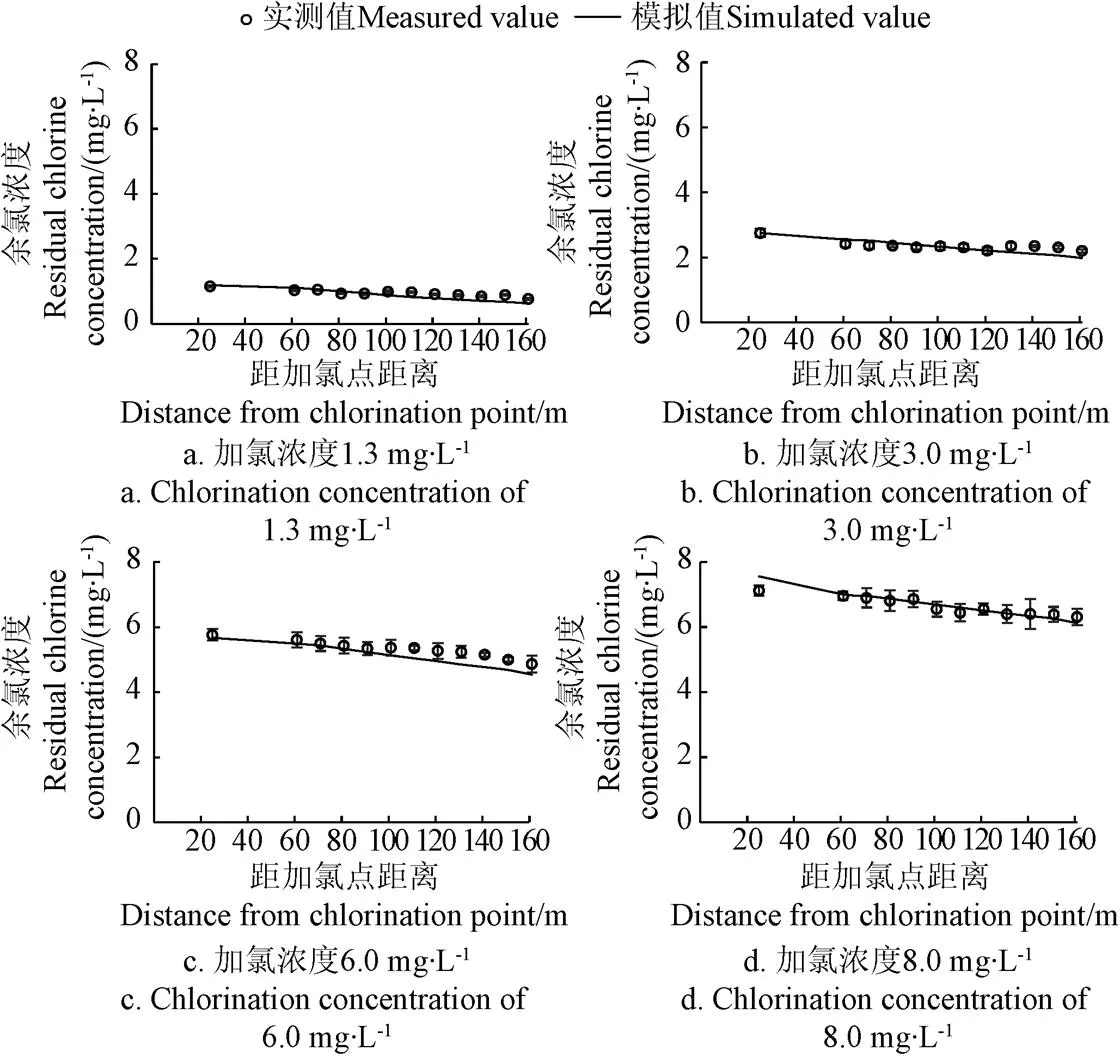
图4 滴灌系统A不同加氯浓度下的不同位置余氯模拟值与实测值比较(率定)
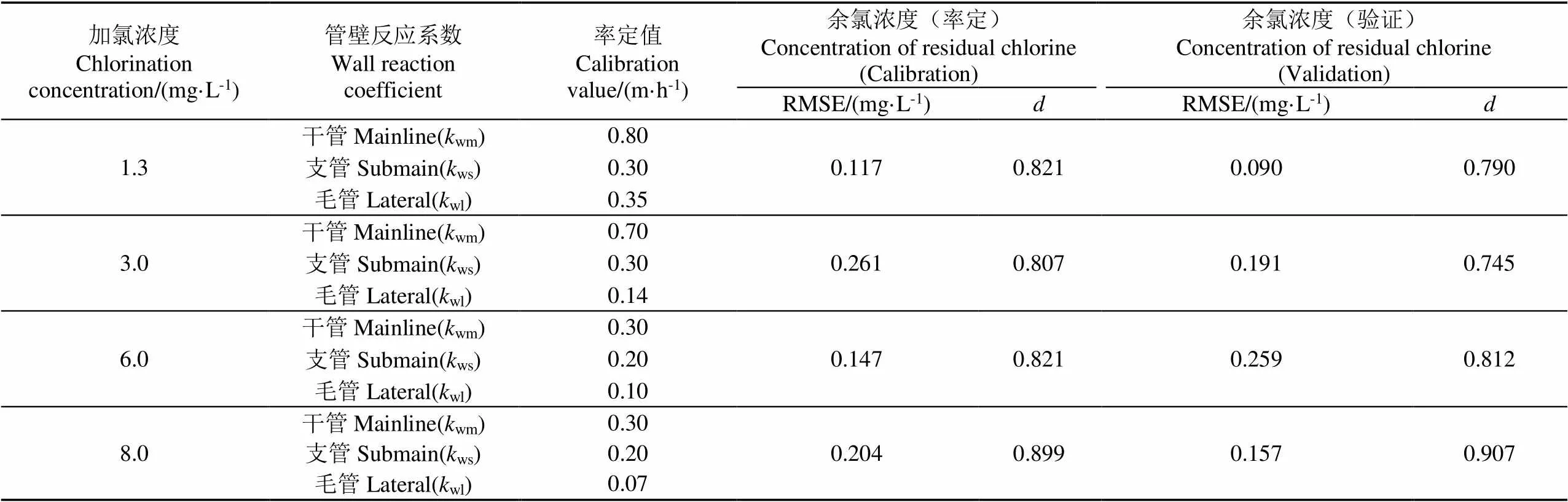
表3 不同加氯浓度条件下管壁衰减系数及余氯模拟评价指标
3 模型应用与结果分析
3.1 模拟方案
模型应用考虑加氯模式(浓度-时长)和毛管长度对滴灌系统余氯浓度及余氯质量分布特征的影响。因水质会对余氯衰减过程产生影响,模拟评估时假定所用再生水水质与第2节中试验条件一致。参照图1滴灌系统,设定模拟模型中干管、支管长度分别为25和10 m,设定毛管数量为10条,以间距为1 m均匀分布于支管上,灌水器间距及模型水力及水质参数设置与第2节中率定结果一致。模拟时在保证加氯质量相同的条件下,设置1.3 mg/L-185 min(C1T4)、3 mg/L-80 min(C2T3)、6 mg/L-40 min(C3T2)和8 mg/L-30 min(C4T1)4种加氯模式。所有模式灌水时长均设定为4 h。为保证有效氯在加氯结束后仍部分存留于系统中,所有模式均先进行灌水,而后开始加氯,即对C1T4、C2T3、C3T2和C4T1模式分别在灌水35、160、200和210 min后开始加氯。毛管长度范围设置为10~150 m,以10 m为间隔进行模拟,计算沿毛管方向水龄(自水源/加氯点运移至管网特定位置处所耗时间)、余氯浓度分布及平均浓度,评价加氯模式及毛管长度对余氯浓度分布的影响;计算灌水单元灌水器流量和灌水器出流余氯质量(∑(灌水器流量×余氯浓度×加氯时间))偏差率S和克里斯琴森均匀系数(Coefficient of Uniformity,CU)评价加氯模式和毛管长度的影响。
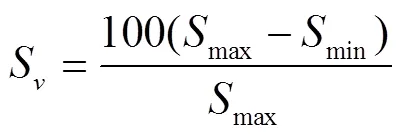
式中max和min分别是灌水器流量(L/h)或出流余氯质量(mg)最大值和最小值。
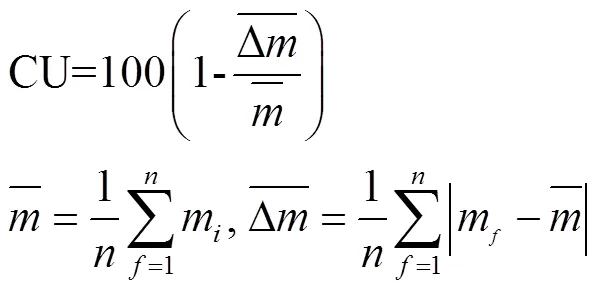
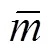
3.2 结果与分析
3.2.1加氯浓度及毛管长度对余氯浓度分布的影响
图5给出了不同加氯浓度条件下典型毛管长度(10、80和150 m)水龄及余氯浓度沿毛管方向变化。由图5可知,系统内不同位置节点水龄差异明显,10、80和150 m滴灌系统沿毛管方向水龄变化范围分别为5.8~12.8、1.2~16.9、1.1~27.3 min,水龄沿远离进水口方向持续增加,在灌水单元后半段,因管段流速降低,灌水器节点水龄增加趋势更为明显。沿毛管方向水龄的变化决定了氯与灌溉水及管壁的反应时间差异[15],是灌水器出流中余氯浓度的关键影响因素。随着氯与水体及管壁的反应,不同加氯浓度条件下余氯浓度均沿远离进水口方向呈现下降趋势(图5)。
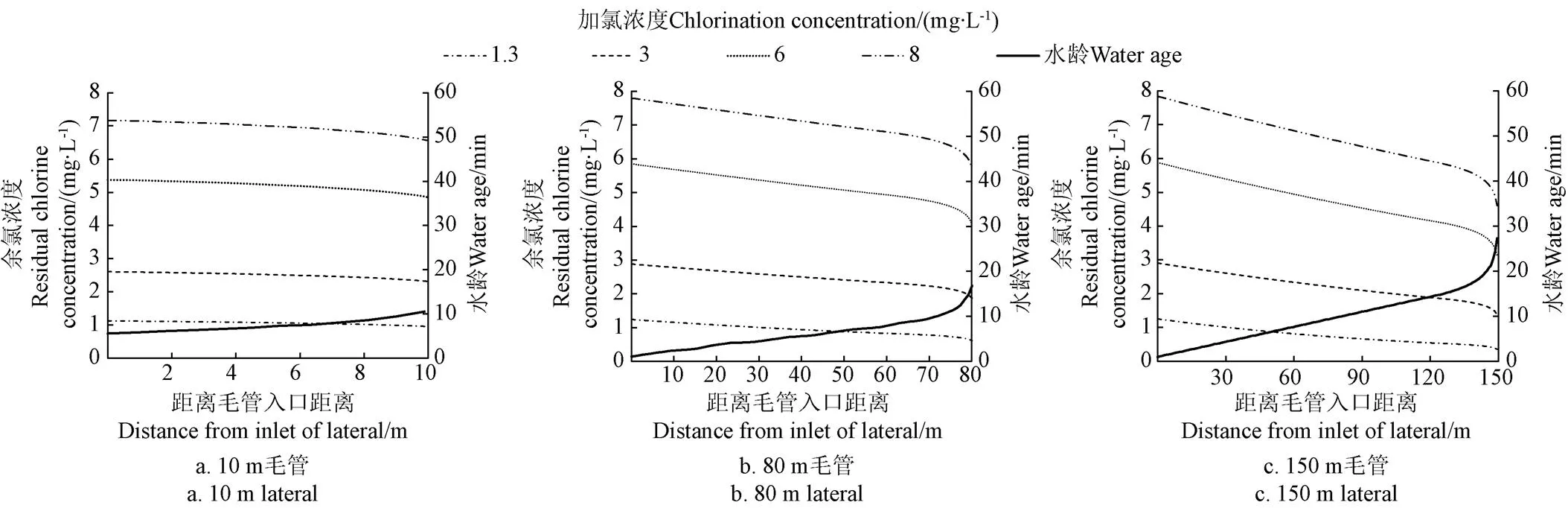
图5 不同加氯浓度典型毛管长度水龄及余氯浓度沿毛管方向变化
同一毛管长度,余氯浓度衰减速度随加氯浓度的增大而减小。例如,毛管长度为80 m时,加氯浓度为1.3和6.0 mg/L时沿毛管方向余氯浓度最大值与最小值之比分别为2.0和1.4,这与试验中低加氯浓度时较大的主体水衰减系数和管壁衰减系数有关。同一加氯浓度,毛管长度不同时,灌水单元中余氯浓度差异基本随毛管长度的增加而增大。例如,对于3.0 mg/L加氯浓度,10、80和150 m毛管长度时余氯浓度最大值与最小值之差分别为0.39、1.00和1.53 mg/L,这是由灌溉水在长毛管滴灌单元中运移时间(水龄)及运移距离差异较大造成的。
图6给出了不同加氯浓度条件下灌水单元平均余氯浓度和平均水龄、毛管末端余氯浓度和水龄随毛管长度增加的变化。由图可知,平均水龄和毛管末端水龄均随毛管长度增加呈先降低而后升高的趋势。毛管长度较短时,较大的平均水龄及毛管末端水龄与灌溉单元控制面积较小而导致的干、支管流速较小有关,这与图5a中较大的毛管首端水龄一致。当毛管长度由10 m逐渐增加到40 m时,干、支管流速逐渐增大,平均水龄下降至最小值;随着毛管长度的进一步增加,平均水龄和毛管末端水龄持续增加。
与平均水龄和毛管末端水龄变化趋势相反,不同加氯浓度系统平均余氯浓度与毛管末端余氯浓度随毛管长度增加呈先升高而后降低趋势,水龄变化导致的有效氯与灌溉水及管壁反应时间的变化是引起这一变化的主要原因。不同加氯浓度条件下,在平均余氯浓度随毛管长度增加至最大值后,随毛管长度进一步增加,平均余氯浓度和毛管末端余氯浓度随毛管长度增加衰减比例均随加氯浓度的增加而减低。例如,对于加氯浓度为1.3 mg/L系统,当毛管长度由40 m逐渐增加到150 m时,平均余氯浓度与加氯浓度比值从82%逐渐降低至60%,而对于8 mg/L系统对应值则仅从91%降低至82%,这与图5中不同加氯浓度处理沿毛管方向余氯衰减规律类似,也与低加氯浓度时较大的主体水衰减系数和管壁衰减系数有关,说明较高加氯浓度条件下平均余氯浓度对毛管长度变化的敏感性相对较弱。由图6b还可看出,毛管末端余氯浓度随毛管长度增加衰减速率大于平均余氯浓度。当加氯浓度为1.3、3、6和8 mg/L时,150 m毛管末端余氯浓度分别为平均余氯浓度的46%、61%、66%和70%。毛管末端余氯浓度、平均余氯浓度和加氯浓度的明显差异给基于毛管末端余氯浓度控制系统加氯浓度、进而防止灌水器堵塞造成了一定困难。

图6 不同加氯浓度灌水单元平均余氯浓度和平均水龄、毛管末端余氯浓度和水龄随毛管长度增加的变化
3.2.2 加氯模式及毛管长度对余氯质量分布特征的影响
图7给出了不同加氯模式及毛管长度条件下灌水单元内灌水器流量和余氯质量偏差率和均匀系数变化。灌水单元内灌水器流量偏差率随毛管长度增加而增加,当毛管由10 m逐渐增加至150 m时,流量偏差率由0.01%增加到23%,以《微灌工程技术规范》(GB/T 50485-2009)[25]中规定灌水单元灌水器设计允许流量偏差率不超过20%为约束条件,仅考虑灌水均匀性情况下本研究所用滴灌带极限铺设长度为136 m,灌水器流量均匀系数对应值为95%。与灌水器流量偏差率呈现规律类似,灌水单元内余氯质量偏差率基本随毛管长度的增加而升高,但所有加氯模式条件下余氯质量偏差率均明显高于灌水器流量偏差率。例如,在毛管长度为10 m时,对于C1T4、C2T3、C3T2和C4T1加氯模式处理余氯质量偏差率分别达到22%、24%、36%和45%。灌水单元内余氯浓度差异是造成余氯质量偏差率较高的重要原因。除此之外,灌水单元内不同灌水器加氯历时差异也是造成这一结果的重要原因。例如,由图5a可知,毛管长度为10 m时,受管网中各灌水器节点水龄不同的影响,对于C4T1模式,自灌水结束前30 分钟开始加氯后,毛管首端和毛管末端加氯历时平均约为24.2和17.2 min。

图7 不同加氯模式及毛管长度条件下灌水器流量和余氯质量偏差率和均匀系数
对比不同加氯模式余氯质量偏差率和均匀系数可知,C2T3加氯模式可以获得相对较低的余氯质量偏差率和较高的余氯质量均匀系数。对于C3T2和C4T1加氯模式,较短的加氯时长导致的灌水器加氯历时相对差异较大是导致高浓度加氯模式余氯质量偏差率较高的主要原因。例如,80 m毛管条件下,C3T2模式加氯历时极差值为15 min,占到系统加氯时长的39%,远高于C2T3模式加氯历时极差占系统加氯时长比值(19%),这说明系统加氯过程中不宜设置过短的加氯时长,以保证灌水单元内不同位置灌水器加氯历时相对差异较小。由图7a还可看出,C1T4加氯模式余氯质量偏差率在不同毛管长度时基本高于C2T3模式,这与低浓度加氯条件下有效氯在管网中的明显衰减有关。综上可知,低浓度-长历时加氯尽管可以降低灌水单元内灌水器加氯历时相对差异,但是由于加氯浓度过小,有效氯在滴灌系统明显衰减也会导致余氯质量偏差率的升高。
参照《微灌工程技术规范》(GB/T 50485-2009)中灌水器设计允许流量偏差率的规定,本研究假定余氯质量偏差率约束条件为40%,由此可推知C1T4、C2T3、C3T2和C4T1模式毛管极限铺设长度分别为55、66、37和20 m,上述极限长度条件下对应余氯质量均匀系数分别为92%、93%、91%和92%,超过90%,说明C2T3模式在保障较高的余氯分布均匀性情况下可以明显提高毛管铺设长度。
4 结 论
本研究基于EPANET软件,构建了再生水滴灌系统水力性能及余氯运移、衰减和分布模型,基于试验数据对模型水力和水质模拟参数进行率定和验证,并应用该模型分析了加氯模式(浓度-时长:1.3 mg/L-185 min、3 mg/L-80 min、6 mg/L-40 min和8 mg/L-30 min)和毛管长度(10~150 m)对系统余氯分布特征的影响,主要结论如下:
1)加氯浓度对氯衰减过程影响明显,氯衰减速度随随加氯浓度的增加而降低。
2)基于EPANET软件建立的再生水滴灌管网模型能较好模拟滴灌管网水力特征及系统余氯分布特征,沿毛管方向灌水器余氯浓度模拟值与实测值均方根误差(RMSE)小于0.26 mg/L,一致性指数达到0.75以上。
3)灌水单元平均余氯浓度与毛管末端余氯浓度随毛管长度增加呈先升高而后降低趋势,高浓度加氯处理平均余氯浓度和毛管末端余氯浓度随毛管长度增加衰减速率相对较小。
4)较短的加氯历时(<40 min)和过低的加氯浓度(如1.3 mg/L)均易造成余氯质量偏差率升高和均匀系数降低;建议使用加氯浓度3 mg/L-加氯时长80 min的加氯模式,该模式毛管极限铺设长度达到66 m,余氯质量均匀系数超过90%。
[1]Wang Zhen, Li Jiusheng, Li Yanfeng. Using reclaimed water for agricultural and landscape irrigation in China: A review[J]. Irrigation and Drainage, 2017, 66: 672-686.
[2]李云开,宋鹏,周博. 再生水滴灌系统灌水器堵塞的微生物学机理及控制方法研究[J]. 农业工程学报,2013,29(15):98-107.
Li Yunkai, Song Peng, Zhou Bo. Microbiology mechanism and controlling methods for emitter clogging in the reclaimed water drip irrigation system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(15): 98-107. (in Chinese with English abstract)
[3]Ravina I, Paz E, Sofer Z, et al. Control of emitter clogging in drip irrigation with stored treated municipal sewage effluent[J]. Agricultural Water Management, 1997, 33(2/3): 127-137.
[4]Cararo D, Botrel T, Hills D, et al. Analysis of clogging in drip emitters during wastewater irrigation[J]. Applied Engineering in Agriculture, 2006, 22(2): 251-257.
[5]Li Jiusheng, Chen Lei, Li Yanfeng, et al. Effects of chlorination schemes on clogging in drip emitters during application of sewage effluent[J]. Applied Engineering in Agriculture, 2010, 26(4): 565-578.
[6]Song Peng, Li Yunkai, Zhou Bo, et al. Controlling mechanism of chlorination on emitter bio-clogging for drip irrigation using reclaimed water[J]. Agricultural Water Management, 2017, 184: 36-45.
[7]Song Peng, Feng Gi, Brooks J, et al. Environmental risk of chlorine-controlled clogging in drip irrigation system using reclaimed water: The perspective of soil health[J]. Journal of Cleaner Production, 2019, 232: 1452-1464.
[8]Li Jiusheng, Li Yanfeng, Zhang Hang. Tomato yield and quality and emitter clogging as effected by chlorination schemes of drip irrigation systems applying sewage effluent[J]. Journal of Integrative Agricultural, 2012, 11(10): 1744-1754.
[9]Hao Fengzhen, Li Jiusheng, Wang Zhen, et al. Influence of chlorine injection on soil enzyme activities and maize growth under drip irrigation with secondary sewage effluent[J]. Irrigation Science, 2018, 36(6): 363-379.
[10]Maier S H, Powell R S, Woodward C A. Calibration and comparison of chlorine decay models for a test water distribution system[J]. Water Research, 2000, 34(8): 2301-2309.
[11]Kang Yuehu, Nishiyama S. Finite element method analysis of microirrigation system pressure distribution[J]. Transactions of the Japanese Society of Irrigation, Drainage and Reclamation Engineering, 1994, 169: 19-26.
[12]Baiamonte G. Advances in designing drip irrigation laterals[J]. Agricultural Water Management, 2018, 199: 157-174.
[13]李援农,朱锋. 基于最大控制面积和最低费用的微灌小区管网优化[J]. 农业工程学报,2015,31(23):80-87.
Li Yuannong, Zhu Feng. Optimization of basic irrigation controlling area network for micro-irrigation based on maximum control area and minimum cost models[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(23): 80-87. (in Chinese with English abstract)
[14]孙傅,陈吉宁,曾思育. 基于EPANET-MSX的多组分给水管网水质模型的开发与应用[J]. 环境科学,2008,29(12):3360-3367.
Sun Fu, Chen Jining, Zeng Siyu. Development and application of a multi-species water quality model for water distribution systems with EPANET-MSX[J]. Environmental Science, 2008, 29(12): 3360-3367. (in Chinese with English abstract)
[15]Mohapatra S, Sargaonkar A, Labhasetwar P. Distribution network assessment using EPANET for intermittent and continuous water supply[J]. Water Resources Management, 2014, 28(11): 3745-3759.
[16]Lamm F R, Ayars J E, Nakayama F S. Microirrigation for Crop Production: Design, Operation and Management[M]. Amsterdam: Elsevier, 2007.
[17]Rossman L A. EPANET 2 User’s Manual[M]. Cincinnati: US Environmental Protection Agency, 2000.
[18]Todini E, Pilati S. A gradient method for the analysis of pipe networks[C]//International Conference on Computer Applications for Water Supply and Distribution. UK, Leicester Polytechnic, 1987: 1-20.
[19]环境保护部. HJ 586-2010:水质游离氯和总氯的测定[S]. 北京:中国环境科学出版社,2010.
[20]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB 19106-2013:次氯酸钠[S]. 北京:中国标准出版社,2013.
[21]Hallam N B, West J R, Forster C F, et al. The decay of chlorine associated with the pipe wall in water distribution systems[J]. Water Research, 2002, 36(14): 3479-3488.
[22]ASAE. S553: Collapsible emitting hose (drip tape): Specifications and performance testing[S]. St Joseph, MI: ASABE, 2003.
[23]Wang Zhen, Li Jiusheng, Li Yanfeng. Simulation of nitrate leaching under varying drip system uniformities and precipitation patterns during the growing season of maize in the North China Plain[J]. Agricultural Water Management, 2014, 142: 19-28.
[24]Charles N Haas, Sankaram B Karra. Kinetics of microbial inactivation by chlorine: I review of results in demand-free systems[J]. Water Research, 1984, 18(11): 1443-1449.
[25]中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局. GB/T 50485-2009 微灌工程技术规范[S]. 北京:中国计划出版社,2009.
Modeling of the residual chlorine distribution in drip irrigation system applying reclaimed water based on EPANET
Wang Zhen1, Hao Fengzhen1,2, Li Jiusheng1※, Li Yanfeng1
(1.,100048,;2.030801,)
Chlorination is an important practice to ensure the safety of drip irrigation system with reclaimed water application. However, the decaying process caused by chlorine reacting with irrigation water and drip irrigation pipeline will adversely affect the uniformity of residual chlorine distribution. The objective of this study was to evaluate the effect of different chlorination modes on the residual chlorine distribution in drip irrigation system using a model, which was constructed using the EPANET software package and could simulate the hydraulic performance and residual chlorine transport, attenuation and distribution in a drip irrigation system. The hydraulic and water quality parameters for the model were calibrated and validated based on the experimental data. The distribution of residual chlorine under 4 chlorination modes (chlorination concentration injected– chlorination duration of 1.3 mg/L-185 min (C1T4), 3 mg/L-80 min (C2T3), 6 mg/L-40 min (C3T2), and 8 mg/L-30 min (C4T1)) and 15 lateral lengths (10-150 m at 10-m intervals) were analyzed. The results showed that the hydraulic performance and residual chlorine distribution in the drip irrigation system were well simulated by the constructed model using the EPANET software. The index of agreement between the simulated and measured residual chlorine concentration of emitter discharge along lateral is above 0.75. The age of water discharged from emitters increased with the distance from the inlet of the lateral, while it ranged from 5.8-12.8, 1.2-16.9, and 1.1-27.3 min for the system with lateral length of 10, 80, and 150 m, respectively. The residual chlorination concentration decreased gradually from the inlet of the lateral due to the reaction of chlorine with water and pipe wall. The decay rate of the residual chlorine concentration decreased with the chlorine concentration injected. The relatively higher decay rate was attributed to the higher bulk reaction coefficient and wall reaction coefficient in the drip irrigation system with low chlorination concentration. Under a given injected chlorination concentration, the system with longer length of lateral produced higher variation of the residual chlorine concentration because of the relatively higher variation of water age. The average residual chlorine concentration of the drip irrigation system increased first and then decreased with increasing length of the lateral. A relatively lower decay rate of the average residual chlorine concentration and the residual chlorine concentration at the end of the lateral was observed for drip irrigation system with high injected chlorination concentration. For example, the ratio of average residual chlorine concentration to chlorination concentration injected decreased from 82% to 60% and from 91% to 82% when the lateral increased from 40 to 150 m for the system with 1.3 and 8.0 mg/L of chlorination concentration, respectively. Much higher deviation of the residual chlorine mass was observed than the water applied for all the chlorination modes. The deviations of the residual chlorine mass for the system with 10-m length of lateral were 22%, 24%, 36%, and 45% for the C1T4, C2T3, C3T2 and C4T1 modes, respectively. The C2T3 mode generally produced the lowest deviation and the highest Christiansen uniformity coefficient (CU) of residual chlorine mass while the length of lateral ranged from 10 to 150 m. A relatively shorter duration of chlorination (smaller than 40 min) and too low injected chlorination concentration (1.3 mg/L) probably produced higher deviation of the residual chlorine mass and thus decreased the coefficient of uniformity of the residual chlorine mass. The injected chlorination concentration of 3 mg/L with chlorination duration of 80 min was recommended, while the maximum lateral length could extend to 66 m with the coefficient of uniformity of residual chlorine mass exceeding 90%.
chlorine; simulation; hydraulic performance; water quality; drip irrigation; EPANET
王珍,郝锋珍,李久生,等. 基于EPANET的再生水滴灌系统余氯分布模型构建[J]. 农业工程学报,2020,36(10):99-106.doi:10.11975/j.issn.1002-6819.2020.10.012 http://www.tcsae.org
Wang Zhen, Hao Fengzhen, Li Jiusheng, et al. Modeling of the residual chlorine distribution in drip irrigation system applying reclaimed water based on EPANET[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(10): 99-106. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.10.012 http://www.tcsae.org
2019-09-15
2020-04-10
国家重点研发计划课题(2016YFC0403103);国家自然科学基金项目(51790531);流域水循环模拟与调控国家重点实验室自由探索课题(SKL2018TS06)
王珍,高级工程师,主要从事灌溉原理及技术研究。Email:wangzhen-686@163.com
李久生,研究员,博士生导师,主要从事灌溉原理与技术研究。Email:lijs@iwhr.com
10.11975/j.issn.1002-6819.2020.10.012
S275.6
A
1002-6819(2020)-10-0099-08

