基于统计和天文周期模型的怀集县年降水预测

王迁，李丹丹，赵玲

（肇庆市气象局，广东肇庆 526040）

随着肇庆经济迅速发展，专业气象服务倍受重视［1］。近年来，气象灾害发生频繁［2］，为了更好为针对怀集地区水电行业做好专业气象服务，提前预报未来年份的降水情况、估测水资源量大小以及预防洪涝发生的概率，年降水量的预报显得十分重要［3］。目前，年降水量预报所有采用的方法很多，其中数理统计的方法仍是比较有效的［4］，即通过寻找各年份降水量之间的相关规律来拟合计算，得出模型方程，并对未来年份降水量进行预测。在国内具有代表性数理统计的方法马尔科夫链应用于预测年降雨量颇为广泛，例如王文圣等［5］提出了在一步转移概率基础上利用马尔科夫链预测了年降水量；徐晓宇［6］、韩璞璞等［7］则考虑多年降水量序列的前后相依关系，进一步提出了加权马尔科夫链预测方法，分别成功预测了北京地区年降水量和庐江县年降水量；王洋等［8］利用加权马尔科夫链预测的泰安地区年降水量与实际情况吻合，并预测了该地区34年后将出现旱情。而天文周期法与之不同［9］，由于大气环流过程与气象要素（气压、气温、降水等）的变化周期与天文周期相对应，因此地面天气也直接或间接受其影响，在原理上具有可行性。普布卓玛等［10］结合天文周期法进行了高原天气预报；广深天地生综合研究小组等［9］介绍天文周期对广东天气过程预报的应用贡献，并利用天气周期作单站气象要素时间曲线，根据天气系统与天气过程的关系，进而预报天气过程和降水量。因此，基于天文周期建立年降水量预报模型，可以忽略诸多因素的影响，仅根据历史数据进行预测评估，对年降水量要素进行统计叠加，并直接作为预报值。

本研究利用基于统计的加权马尔科夫链法和天文周期法建立年降水量模型，对怀集县2009—2018年近10年年降水量进行预测，并通过与实测值进行对比，评估预测方法的可行性，以期对水电专业气象服务中长期预报方面做出参考。

1 统计模型和天文周期模型建立

统计法，即寻找各随机变量之间的相关规律来定量描述，通过对内在发现进行精确判断和预测的数学工具［11］。本研究基于统计法的加权马尔科夫链降水预测模型，并与天文周期模型同时对未来年份降水量进行预测和评估。

1.1 移动平均分析模型

对序列｛xt｝的几个前期值和后期值取平均，得到一个新序列｛yt｝，使得原序列光滑，这就是移动平均法［12］。数学表达式为

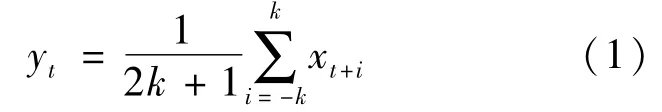
当k＝1时，就是3点滑动平均。移动平均能够清晰直观的显示出序列的某种趋势并且能减弱随机的因素。

1.2 马尔科夫链

马尔科夫链［13］是指时间和状态都离散的随机过程，是一种状态变化为另一种状态的理论研究，即通过利用不同状态初始概率和状态间的转移概率来确定状态的变化趋势。设状态区间I＝｛1，2，3…｝，转移状态p ij为元素矩阵。

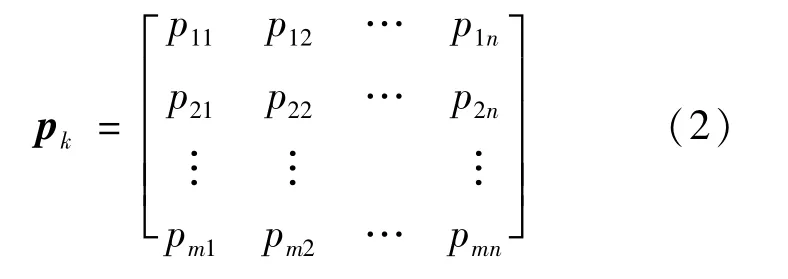
矩阵为k步转移矩阵，本研究仅使用齐次马尔科夫链。

年降水量属于时间序列，具有时间规律，但同时也具有独立性和相依性，导致随机成分易被忽略，通常利用自相关性分析研究降水序列的随机成分。设立自相关系数rk，公式为

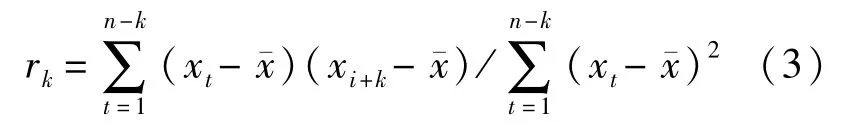
其中，k为阶数；xt表示第t年降水量（mm）；表示逐年降水量序列平均值（mm）；n为年降水序列长度。权重系数pk公式为

其中，m为预测需要计算的最大阶数。

1.3 天文周期模型

采用月亮、地球运动和太阳活动的长周期，即选用太阴周期18、19年，太阴近点周期9、18年，太阳周期11、13、22、24、26年，地极移动周期13、19、25、26年等4个系列共13个周期，对所要预报的要素和时段，计算上述13个周期的某单站某气象要素值的迭加平均值，数学表达式为

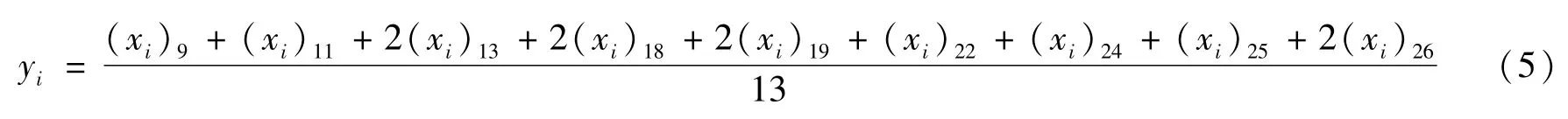
其中，yi表示所有预报的某站某年某要素值（即与预报年相同的各周期年份该要素叠加平均值，为预报值），下标9，11，…26，表示距预报年份之前的第9年、第11年，…，第26年，xi表示某种要素值，yi为预报值。

2 模型验证分析

2.1 怀集年降水量特征和异常变化分析

图1为怀集县1958—2018年年降水量数据经过3次多项式拟合的曲线。由图1可知，1958—2018年怀集的年降水分布较分散，波动较大，存在极端降水的情况。

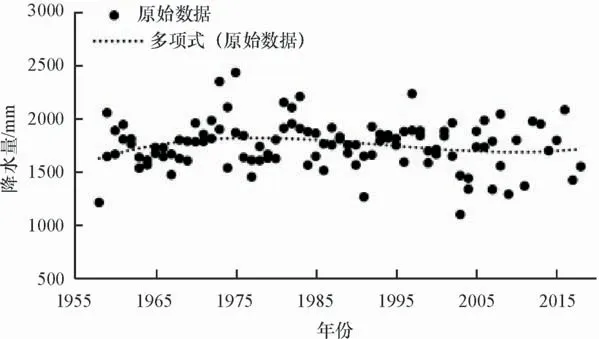
图1 1955—2018年怀集县降水量拟合曲线

因此本研究采用均值-标准差分级法［8］，对怀集地区年降水量进去分级，状态分为特多、偏多、正常、偏少、特少等5个等级，方法如表1所示。经计算，怀集地区降水量x均值＝1 744.7 mm，标准差S＝270.8，平稳性较差，因此怀集地区降水属于随机序列。加权马尔科夫链预测模型则针对这种随机序列进行动态预测，能够处理波动随机性大的问题。

表1 怀集地区年降水量分级

2.2 移动平均分析和线性回归模型拟合

图2为怀集县1958—2008年年降水量一元线性回归和3年滑动平均图。年降水量序列是时间序列，在时间上有一定的规律［14］，但年降水量的相依性和独立性，导致序列中随机成分往往被忽略。本研究通过数理统计的方法先对原有年降水量序列进行3年滑动平均分析，（令k＝1）得到新的年降水量序列，从而减弱初始降水序列中随机因素的影响［14］，降低误差，以新序列进行一元线性回归模型拟合，如图2光滑曲线所示得到一元线性回归方程。由表1和图2可以看出，怀集县1958—2018年年降水整体呈稳定趋势，均在1 744.7 mm左右波动，其中1958、1991、2003、2004、2011、2017年降水显著偏少，降水量少于1 446.83 mm属于枯水年景；1959、1973、1981、1983、1997、2016年降水显著偏多，降水量多于2 042.63 mm属于丰水年景。根据图2线性分析得到，怀集县年降水量50多年来有着缓慢减少的趋势，从1978年开始，每10年约减少7.45 mm。

图2 1958—2018年怀集县年降水量的年际变化、线性回归和3年滑动平均曲线

2.3 基于加权马尔科夫链预测模型在怀集年降水量预测结果评估

1）预测过程。

怀集地区的频数转移矩阵和转移频率矩阵如下所示：

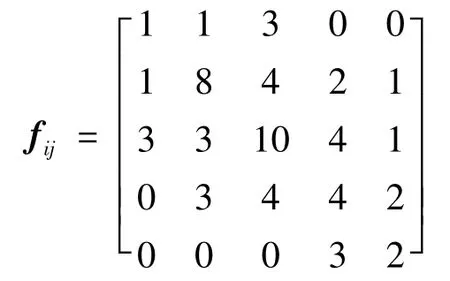
由式（3）计算各滞时自相关系数分别为0.521 2、0.273 8、-0.122 4、-0.106 5、0.159 0；由式（4）计算各滞时权重分别为0.440 6、0.231 4、0.103 5、0.090 1、0.134 4。根据2013—2017年的年降水量数据，利用1～5阶的权重，对2018年年降雨量进预测，如表2所示。得出加权和：i＝（0.070 9 0.099 1 0.411 6 0.321 5 0.097 0）。通过均值向量与加权向量乘积，得出2018年年降水量：P＝·＝1 788.5 mm。重复以上过程即可计算2009—2018年年降水量，如表3所示。

表2 2018年降水量预测过程流程

2）预测结果评估。

表3为基于加权马尔科夫链模型的怀集县2009—2018年年降水量预测值与实测值。从检验分析结果来看，整体的预测值相对误差基本都在20%以内，10个结果中有7个结果小于20%，基本满足预测结果要求。其中2010、2014、2015年相对误差小于5%（占比20%），3个结果相对误差小于10%（占比30%），7个结果相对误差小于20%（占比70%），3个结果绝对误差小于100 mm（30%），总体来说，预测结果基本达到要求，具有一定的预测能力。但部分预测结果并不符合要求，2009、2011和2017年属于枯水年，预报误差较大，达不到要求。而对于2016年属于丰水年，其预报结果较为满意，绝对误差不到6%。数理统计学虽然利用了降水时间序列的均值和均方差，但预测值趋于某一状态时是具有规律性的，预测值考虑气象坏境和极端天气概率较小，因此极端条件会出现误差，达不到预报。

表3 基于加权马尔科夫链模型怀集县降水量预测值与实测值

2.4 基于天文周期模型的怀集年降水量预测结果评估

表4为基于天文周期模型怀集县2009—2018年降水量预测值与实测值。通过统计距预报年份之前的第9、11、13、18、22、24、25、26年的年降雨量，并计算得出怀集县2009—2018年的年降雨量，从年降水量预测结果来看，整体的预测值相对误差也基本都在20%以内，基本满足预测结果要求。结果显示，其中2010、2014、2015年相对误差小于5%（占比30%），6个结果相对误差小于10%（占比60%），8个结果相对误差小于20%（占比80%），3个结果绝对误差小于100 mm（30%），总体来说，预测结果满意度达到要求。但部分预测结果也并不符合要求，2009、2011、2016年预报误差较大，达不到要求。天文周期模型虽然可以忽略部分因素影响，但遇到小气候环境，仍然需要用气象因素作为加权项进行约束。

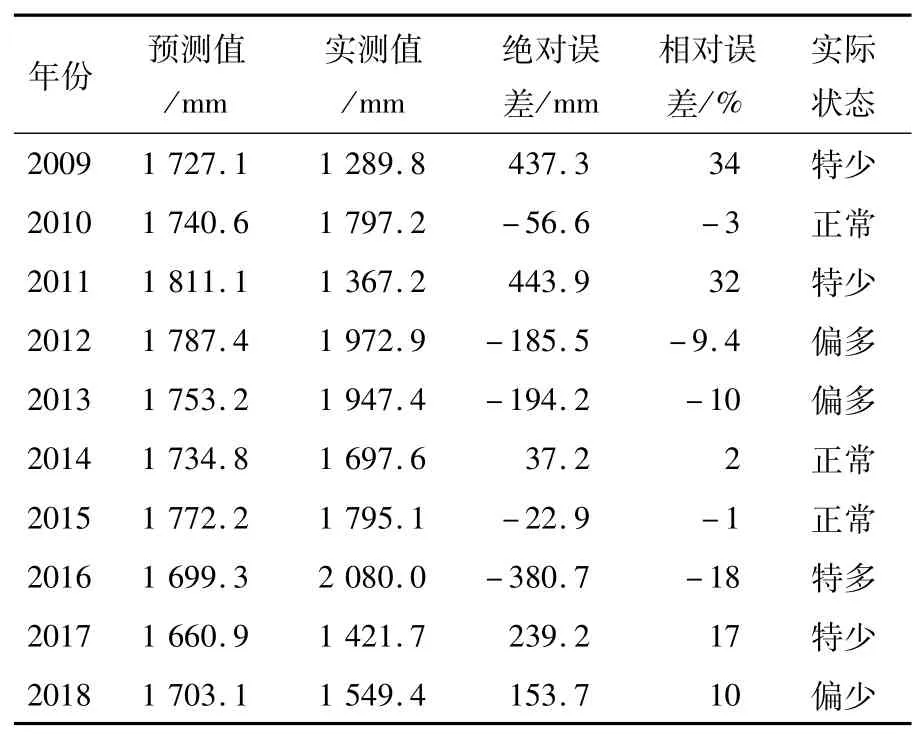
表4 基于天文周期模型怀集县降水量预测值与实测值

通过对表3和表4的结果进行比较，发现在2009、2011和2017年的枯水年预报结果均不太满意，即预报年降水量趋势均为正常降水量值，与实际预报结果“特少”，存在较大误差，因此均未考虑到气象环境影响和极端天气出现概率。而对2016年的丰水年，马尔科夫链的预测结果为“特多”与实际降水量值相吻合，预测效果较好；整体的建模过程来看，加权马尔科夫链模型建立稍显复杂，需要大量的数据作为支撑，容易受限于气象数据预报的时间序列较短的情况，相比较，天文周期数据处理比较简单。在今后大数据计算情况下，考虑时间的随机和数据状态的偶然性时，加权马尔科夫链将更为实用。

3 结论

本研究先把年降水量时间序列进行3年滑动平均，消弱初始时间序列的随机性和偶然性，降低了干扰因素，增加降水时间序列的规律性，在新的序列基础上，再利用加权马尔科夫链建立预测模型。因此，在应用中长期预报，移动平均可以有效降低干扰因素，提高规律性，使得预报有迹可循，在移动平均的基础上，再次利用自相关性降低降水量序列的随机成分，使得降水量序列从内部相依规律和预测结果形式均增加权重和约束条件，进一步提高预报的准确性和可靠性，这种方法也值得推广。

本研究通过加权马尔科夫链模型和天文周期模型分别对怀集县2009—2018年的年降雨量进行预报，结果显示两种方法均能达到预报基本要求，其中加权马尔科夫模型在预测丰水年时满意度更高；两种模型对非极端天气影响下的预报结果均未能达到满意程度。这两种方法均存在单方面问题，即忽略大气环境因素的影响，具有局限性。枯水期和丰水期加大了这两种方法的预报难度，造成误差过大，达不到预期要求。仍需考虑气象要素作为加权项［15］，通过加大约束条件，以期达到预报精细化的目标。天文周期模型比较简单，对于数据要求不高，但考虑随着气象数据的逐渐庞大，在处理大数据和大量随机性与独立性事件，加权马尔科夫链会更为实用。