DQFEM求解正交各向异性薄板单元静力问题

邓小环，许华南，陈水梅，黄清云

（龙岩学院 资源工程学院，福建 龙岩 364000）

1 理论基础

通过采用DQFEM（微分求积有限元法）[1]，分析正交各向异性薄板单元[2]，并将所求得与有限元软件Abaqus所得结果进行比较，进一步验证微分求积有限元法的精确性。

本文采用薄板理论[3]，即不考虑横向剪切变形。在弹性力学中，将两个平行的面和垂直于这两个平行面的棱柱或柱体所围成的物体称为板，如图1所示即为矩形薄板示意图。

图1 矩形薄板示意图Fig.1 Schematic diagram of a rectangular plate

利用薄板理论在分析平板弯曲时假设[4]，将平板弯曲问题简化为二维问题，且全部应力和应变可以用板中面的挠度w表示，即：

2 DQFEM求解正交各向异性材料薄板问题

2.1 二维函数的微分求解法则

对于二维函数f（x,y），通常可用两个一维函数的积表示[5]，即：

经典的微分求积方法通常适合用于矩形区域[6]。根据微分求积法则，一维函数p（x）在结点xi处对坐标x的r阶导数和q（y）在结点yi处对坐标y的s阶导数可由结点函数值分别表示为：

为方便推导二维微分求积有限单元矩阵，引入以下矩阵和向量：

由下面的递推关系可得到权系数为：

2.2 DQFEM求解薄板单元

对于线弹性问题，总势能泛函包括应变能和外力势[7]，即：

式中：ε和D分别是应变向量和材料矩阵；u是位移向量；q是荷载向量。

结构的动能泛函为：

对于薄板弯曲问题，挠度函数也可用拉格朗日函数表示[8]为：

薄板的本构关系：

因为εz=0，γzx=0，γzy=0，可得：

其应变-位移关系[9]为：

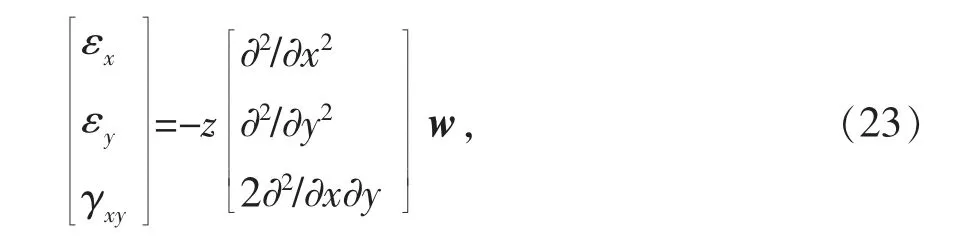
定义如下向量：

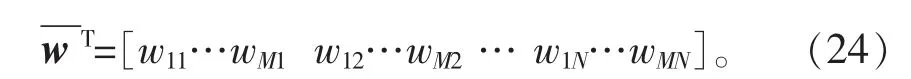
应用微分求积法则，可得结点应变向量为：

将式（25）和式（22）带入式（17）和式（18），离散薄板势能泛函为：

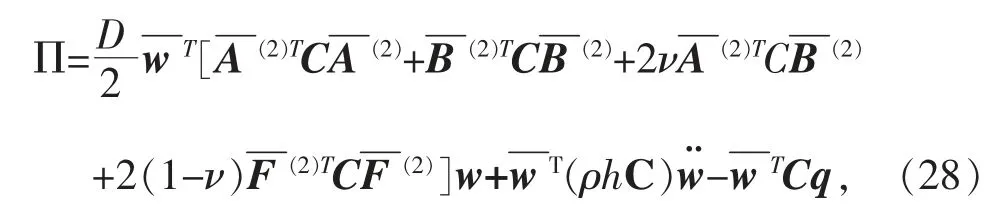
C=diag（Ck），其中分别为x和y方向的高斯-洛巴托积分系数，

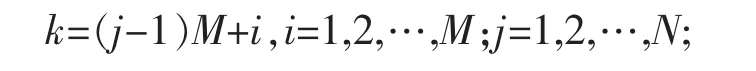
q为结点荷载列向量，其形式同式（24）。

为了满足薄板单元之间的C1连续条件，施加固支边界条件需要对位移向量做一些修正。边界结点参数应该既包括结点挠度，也包括转角，于是有：

式中：wkx=（∂w/∂x）k，wky=（∂w/∂y）k，wkxy=（∂2w/∂x∂y）k。

为方便书写转换矩阵T，此处设板x方向结点数M=2，y方向结点数N=2，则：

则转换矩阵T为：

将式（30）带入式（28），并进行变分，得到与结点位移向量w相对应的微分求积有限薄板单元的质量矩阵、刚度矩阵和荷载列向量，即：

综上可得：

2.3 算例

薄板如图1所示，板长宽均为1，板厚h=0.01，板密度为1，弹性模量E=1，泊松比v=0.3，x方向结点数为M，y方向结点数为N。薄板对侧两边界约束条件为简支约束，在结点上施加均匀力为1N的力，计算板固定结点的位移值，并与有限元软件的计算结果进行对比。如下分别为网格密度为10×10，20×20，30×30，40×40，50×50，100×100薄板示意图：

图2 薄板有限元软件网格密度示意图Fig.2 Grid density diagram of thin plate finite element software

通过DQFEM对上述4种网格密度进行编程分析，取薄板相同位置的结点位移值，得到如下表1至表3所表示的位移值。

表1 有限元软件与DQFEM计算薄板结点位移值及误差对比Tab.1 Comparison of finite element software and DQFEM for calculating plate node displacement values and errors

表2 DQFEM计算薄板结点位移值及误差对比Tab.2 The calculation of displacement value and error comparison of thin plate node by DQFEM

表3 有限元软件计算薄板结点位移值及误差对比Tab.3 The displacement value and error comparison of thin plate node calculated by finite element software

由表2可得采用DQFEM计算得到的薄板结点位移值，网格大小对于位移值取值影响不大，即该方法可采用较少的结点数解决问题。由表3可知采用有限元软件得到的位移值随网格大小的不同而相差较大，表1则说明有限元软件需要更密的网格才能接近采用DQFEM计算得到的位移值，进一步说明DQFEM方法的高效性及精确性。

3 小结

对于正交各向异性薄板单元，采用微分求积有限元法离散最小势能原理的泛函，通过相应的Matlab程序得到所求问题的刚度矩阵，并最终得到正交各向异性薄板单元在受压工况下的位移值，并采用有限元软件ABAQUS中各向异性壳单元模拟了相应的工况，数值模拟结果和上述所求计算结果进行系统对比分析，进一步验证了微分求积有限元法的精确性。