控制系统参数对伺服动刚度的影响

郝亚明

(中国煤炭科工集团 太原研究院有限公司， 山西 太原 030006)

0 引言

伺服驱动系统在很多精细作业机电设备中广泛应用。系统伺服动刚度是决定系统控制精度的重要因素，而系统伺服动刚度受外部负载和控制系统参数影响很大。虽然通过Bode图可直观地显示控制系统参数在不同扰动下对伺服动刚度的影响效果，但只能展示基本变化趋势。在实际应用中，要明确知道伺服动刚度与控制系统参数的对应关系。通常衡量和评价伺服动刚度的标准是用其幅值。为了使问题突出，假设伺服动刚度幅值与控制系统参数之间关系的研究是在固定频率扰动下进行，在任意频率扰动下，同样可以找到一般性规律，直观地展示控制系统参数对伺服动刚度幅值的影响。

1 伺服动刚度数学模型

在交变外载荷的作用下，伺服动刚度是指进驱动系统抵抗位置偏差的能力。伺服动刚度Ksp用下式表示[1]：

(1)

式中：ω为外载荷交变频率，Hz；Tdis(jω)为干扰交变力，N；θo(jω)为变形量，μm。

由式(1)可以看出，伺服动刚度随ω进行变化。ω等于零，意味着系统受到的干扰力为静力，这时系统的伺服动刚度与伺服静刚度相等；ω不等于零，系统的伺服动刚度随ω的变化而变化。在ω与机械系统的固有频率接近或相等时，系统的伺服动刚度降低到最小值。当系统的伺服动刚度低到一定程度时，系统的工作会受影响，降低了设备的作业准确性，精细作业无法完成。

伺服电动机构成进给系统。图1为控制系统简化框图。输出位置偏差由外界干扰引起，伺服动刚度是抗拒干扰的能力，伺服动刚度值越大，抗拒干扰的效果越好，相应位置偏差会越小。给定一个零输入条件，图1可以转化为图2所示的干扰输入作用下位置输出的传递函数框图。可以看出，将干扰作为输入，位置输出的传递函数的倒数刚好是系统伺服动刚度[2]。

图1 控制系统简化框图

图2 干扰输入引起的位置输出的传递函数框图

干扰输入与其引起的位置输出的传递函数表示为：

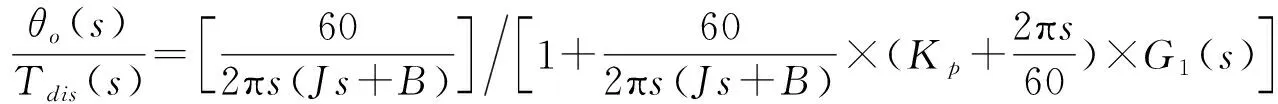
(2)

将式(2)进行化简，得到：

(3)

由文献[2]可知伺服动刚度为：

(4)

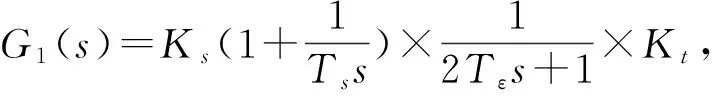
(5)

3 系统参数对伺服动刚度幅值的影响

通常伺服动刚度幅值变化衡量性能优劣[3]，用MATLAB软件进行数值模拟，用曲线图直观展现固定频率扰动作用下伺服动刚度与控制系统参数间的关系。

3.1 位置环比例增益Kp对伺服动刚度幅值的影响

图3为的系统在100 Hz固定频率扰动下Kp对伺服动刚度幅值的影响曲线。由图3可以看出，随着Kp的增加，系统伺服动刚度幅值也在相应上升，说明在固定频率100 Hz干扰下，提高伺服动刚度可以用增加系统Kp的方法。

图3 Kp对伺服动刚度幅值的影响曲线

3.2 速度环比例增益Ks对伺服动刚度幅值的影响

图4为系统在100 Hz固定频率扰动下Ks对伺服动刚度幅值的影响曲线。由图4可以看出，随着Ks的增加，系统伺服动刚度幅值也在相应上升，说明在固定频率100 Hz干扰下，提高伺服动刚度也可以用增加系统Ks的方法。

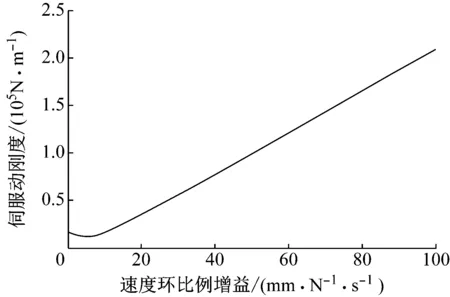
图4 Ks对伺服动刚度幅值的影响曲线

3.3 速度环积分时间常数Tn对伺服动刚度幅值的影响

图5为系统在100 Hz固定频率扰动下Tn对伺服动刚度幅值的影响曲线。由图5可以看出，随着Tn的增加，系统伺服动刚度幅值急剧下降，说明在固定频率100 Hz干扰下，Tn不能太大，否则伺服动刚度降低到一定程度就无法支撑系统正常工作。

3.4 转动惯量J对伺服动刚度幅值的影响

图6为系统在100 Hz固定频率扰动下J对伺服动刚度幅值的影响曲线。由图6可以看出，系统伺服动刚度与J的关系不大。

图5 Tn对伺服动刚度幅值的影响曲线

图6 J对伺服动刚度幅值的影响曲线

3 结论

通过系统分析方法导出系统模型，确定了系统伺服动刚度，以此为基础应用MATLAB软件模拟了特定频率扰动下伺服动刚度幅值随控制系统参数变化的曲线。通过以上数值模拟分析得出下面结论：

1) 在低频扰动作用下，增大位置环比例增益、增大速度环比例增益和减小速度环积分时间常数是提高系统伺服动刚度的直接有效方法。

2) 转动惯量的变化对系统伺服动刚度的影响不明显，用改变转动惯量来提高系统伺服动刚度的效果不显著。

3) 对于中高频干扰作用下伺服动刚度幅值与控制系统参数和转动惯量之间的关系，与以上低频扰动作用相似，分析方法可以借鉴[4]。

4) 以上分析系统伺服动刚度以直接电动机驱动伺服系统为模型。该分析方法具有普遍意义，同样适用于分析其他电动机驱动的系统。