江西省潜在蒸散量模型适用性研究

邱卫华，严 蓓

（江西省上饶市玉山县水利局，江西 玉山 334700）

0 引言

潜在蒸散量又称为参考作物蒸散量（Reference crop evapotranspiration，ET0），作为估算作物实际蒸散及灌溉制度制定的重要参数，其准确估算方法的研究一直是国内外研究的热点[1～3]。ET0获取最精确的方法为蒸渗仪实测法，但这种方法成本较高，在全国范围内难以实现[4，5]。国际粮农组织FAO-56分册推荐Penman-Monteith（PM）公式为计算ET0的标准方法，该方法包括了辐射项与空气动力学项，综合考虑了辐射、湿度、风速、温度等气象因素，保证了方法的计算精度[6，7]。但该方法由于需要的因素较多，在气象因素缺失的地区应用受到了限制，因此对于ET0简化计算方法的研究成为了热点。

温度是现有条件下最易获得的气象数据之一，同时温度是影响ET0产生的主要因素之一，因此，基于温度资料建立适用于区域的ET0精确计算模型十分重要。Almorox等[7]以全球为研究区域，基于全球4 362个气象站点，研究比较了11种温度资料计算ET0模型的精度，并找出了适用于不同区域的不同最优模型；冯禹等[8]研究了温度资料条件下广义回归神经网络模型和小波神经网络模型在四川盆地中的计算精度，并将计算结果与Hargreaves模型比较，指出2个模型在仅考虑温度资料的条件下，表现出了较高的精度；同时随着机器学习模型研究的不断深入，输入相同资料下的机器学习模型精度普遍高于传统经验模型，王升等[9]、Abdullah等[10]均得到了类似的结论。

江西省位于我国华东地区，是国内著名的“鱼米之乡”和重要的水稻生产基地。区域属亚热带季风气候区，土壤以红壤为主，蓄水能力较差，长年的季节性干旱在一定程度上限制了当地经济及农业的发展[11]。本文以江西省为研究区域，基于极限学习机模型（ELM）、支持向量机模型（SVM）、随机森林模型（RF）和M5树模型（M5T），在仅用温度资料条件下模拟当地ET0，并将模拟结果与PM模型和Hargreaves模型（HS）计算结果比较，得出适用于江西省ET0计算的标准模型。

1 研究区域概况与研究方法

1.1 研究区域概况及数据来源

江西省 （N24°29′14″～30°04′41″，E113°34′36″～118°28′58″）空气湿润，雨量充足，多年平均降水量在1 630mm左右，温度适中，年平均气温11.6～20℃，全省冬暖夏热，无霜期长达240～307天，年日照时数1 600h左右。本文选择江西省区域内南昌、南城、景德镇、吉安、赣州5个气象站点1961～2017年的逐日气象数据，计算不同站点的ET0，得出最优模型。

本文数据均来自于中国气象网站，数据控制良好，气象资料主要包括站点日最高气温（Tmax）、最低气温（Tmin）、日照时数（n）、相对湿度（RH）和10m处风速（U10）。

1.2 研究方法

1.2.1 Penman-Monteith模型（PM）

Penman-Monteith（PM）模型为ET0计算的标准模型，其模型型式及参数意义见文献[12]。

1.2.2 Hargreaves模型（HS）

Hargreaves（HS）模型仅考虑温度，可较高精度模拟ET0，具体公式如下：

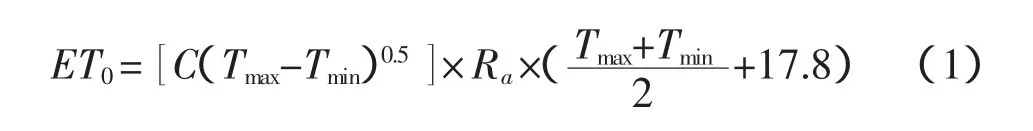
式中，Ra为大气顶层辐射，（MJ m-2d-1）；Tmax、Tmin为最高、最低温度，（℃）；C为常数。

1.2.3 极限学习机模型（ELM）

极端学习机（ELM）可以克服传统神经网络缓慢收敛的缺点，并已广泛应用于回归测试和模型预测领域[13]。ELM模型可以分为3个部分：输入层、隐藏层和输出层（详见图1）。首先，通过输入层输入变量，输出层权重βjk。输出变量矩阵由权重ωij和隐藏层计算。

图1 ELM模型原理图

1.2.4 支持向量机模型（SVM）

支持向量机模型（SVM）被认为是当前小样本统计估计和预测学习的最佳理论。该模型取代了传统的经验最小化与结构经验最小化，这可以克服神经网络的许多缺点，具体模型训练步骤可见文献[14]。

1.2.5 随机森林模型（RF）

随机森林模型（RF）训练期间引入随机属性选择，基于随机性和差异提取数据，可以大大提高决策的准确性，具体模型训练步骤见文献[15]。

1.2.6 M5树模型（M5T）

M5树模型（M5T）可在扫描所有可能的分裂后选择预期的标准偏差，保证模型精度。组成模型的过程分为两部分。首先，将数据分成若干子集以创建决策树。然后通过模型计算子集的预期误差，精度计算公式如下：

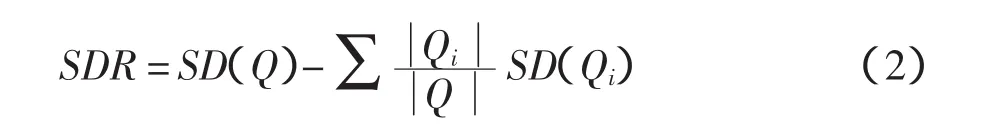
式中，SD和SDR是标准偏差；Q是一组目标样本；Qi是Q的一个子集。

1.2.7 模型训练与模拟

ELM模型、SVM模型、RF模型和M5T模型4种模型主要通过输入温度资料来进行模拟，分别用Tmax、Tmin和Ra以ET0为输出参数。机器学习模型以1961～2000年的逐日数据训练模型，以2001～2017年的数据测试模型精度。模型计算均采用Matlab2018a进行，模型参数取值如表1。

表1 模型参数计算表

1.2.8 模型精度指标

均方根误差（RMSE），确定系数（R2）和效率系数（Ens）用于评估模型，具体公式如下：

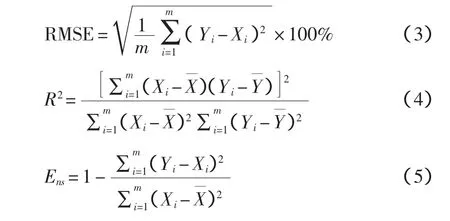
式中，Xi和 Yi分别为标准值和预测值；为 Xi的平均值。

由于评价指标过多，无法统一对模型精度进行比较，因此需引入GPI指数综合衡量各指标的大小，评估模型精度：

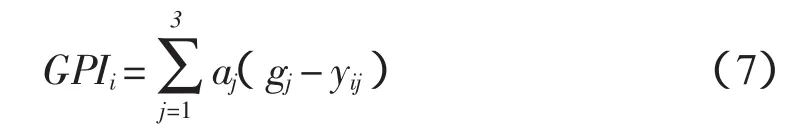
式中，αj为系数，其中 RMSE 取 1，Ensand R2取-1；gj为评价指标的中位数；yij为评价指标的缩放值。

2 结果与分析

2.1 ET0日值拟合结果

图2为不同模型在不同站点ET0日值与PM模型计算值的拟合结果。由图中可以看出，不同模型拟合结果存在一定的差异。ELM模型在不同站点的拟合效果最好，拟合方程斜率分别为1.106、0.973、1.151、1.090和1.055，与标准值“1”最为接近。SVM模型的精度次之，在5个站点的拟合方程斜率分别为0.858、0.790、0.895、0.877和0.888，RF模型和 M5T模型的精度较低，而HS模型的精度最低，与PM模型计算结果的拟合方程斜率仅为 0.548、0.583、0.652、0.642 和 0.624，与标准值“1”的差距较大。

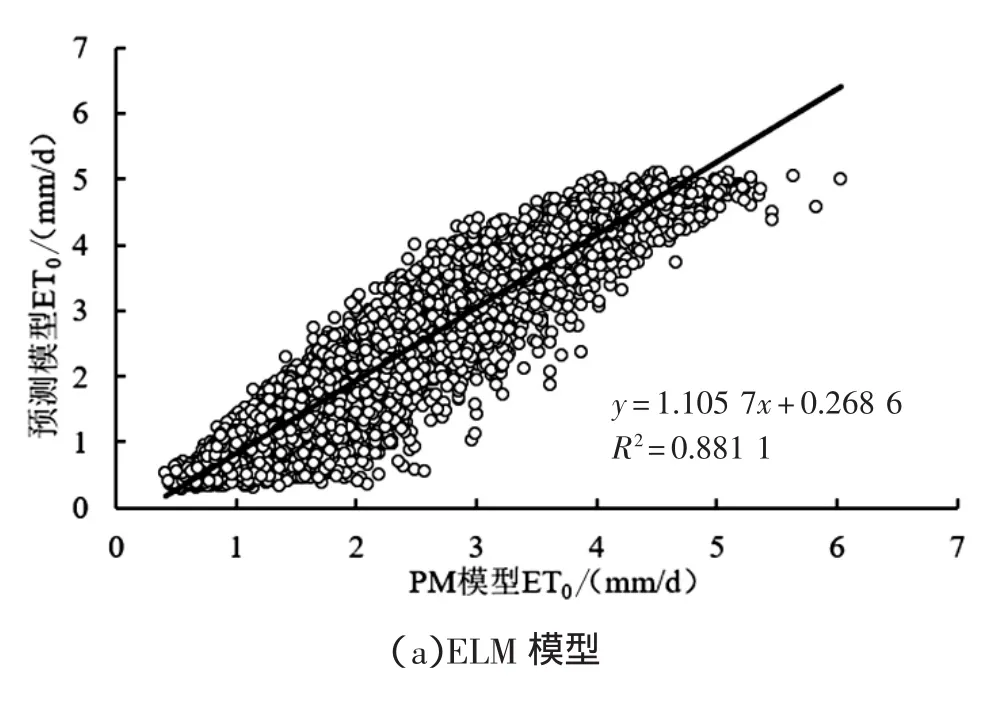
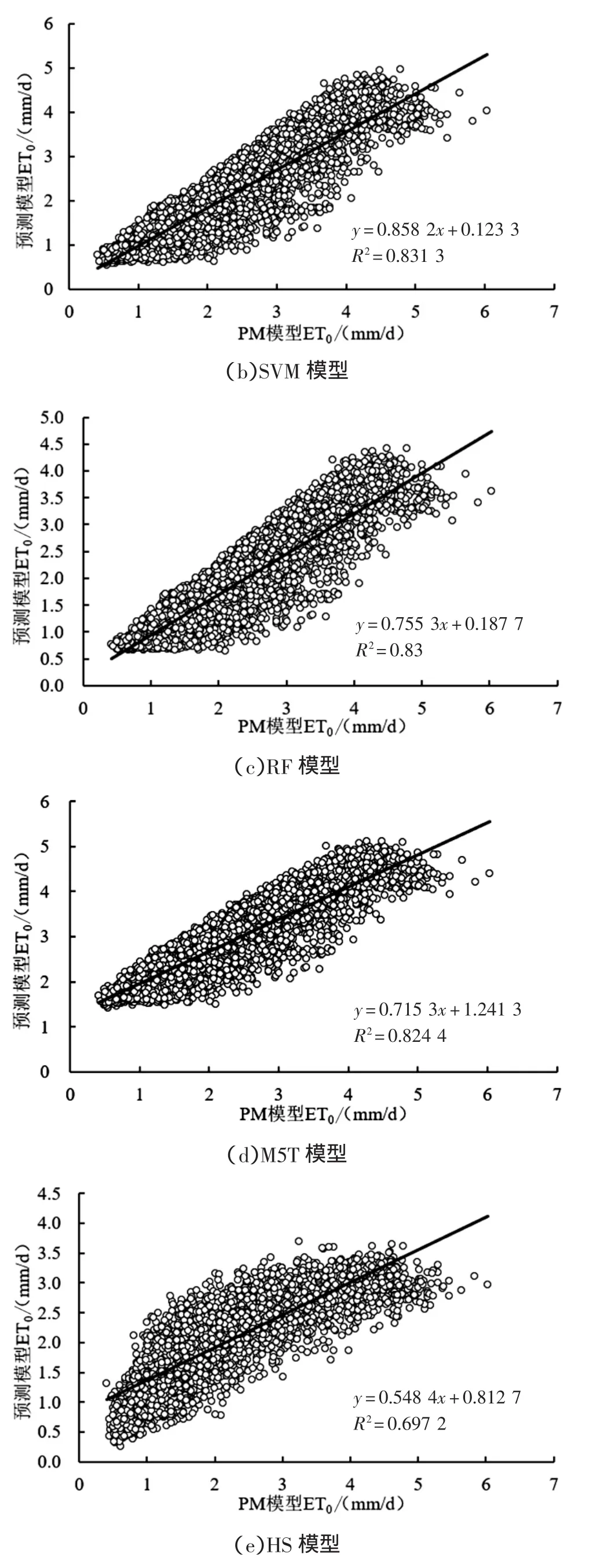
图2 南昌站PM模型与预测模型ET0拟合结果分析

2.2 ET0月值拟合结果

图3为不同站点不同模型ET0月值计算结果对比。ET0月值计算结果可更好地反映ET0的年内变化趋势，为表征模型精度高低，常需从日值和月值2个角度进行评估，分析数据的年际变化趋势和年内变化趋势。由图中可以看出，不同模型计算得出的ET0值在多年年内的变化趋势基本一致，均呈开口向下的二次抛物线型式。不同模型ET0在11月、12月、1月、2月的值普遍较低，约80%的ET0均集中在了3～10月的主要作物生长季。不同模型ET0月值计算的精度不同，其中ELM模型和SVM模型的计算结果与PM模型计算结果变化趋势较吻合，而M5T模型和HS模型在5个站点ET0月值的精度误差较大。

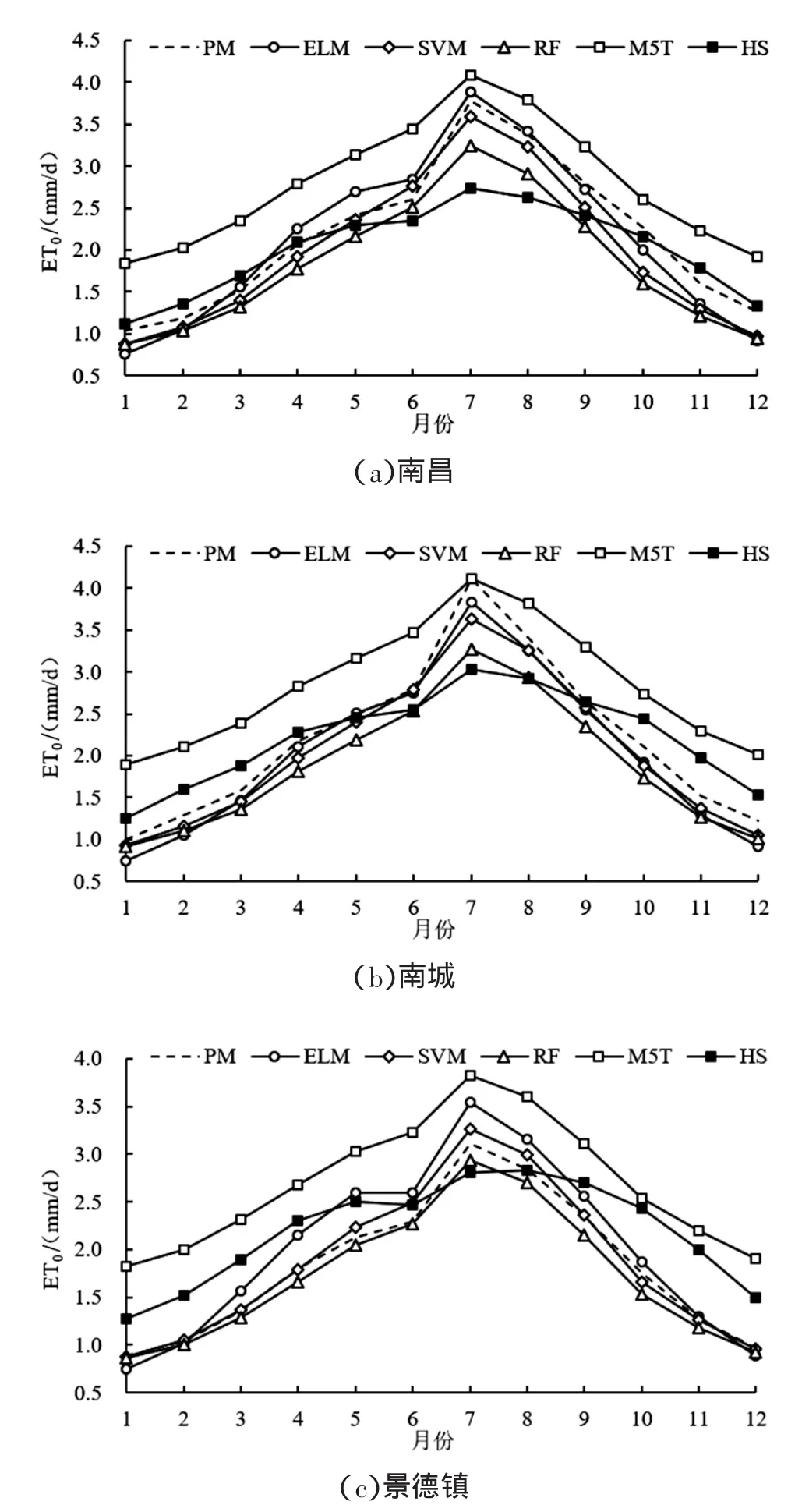
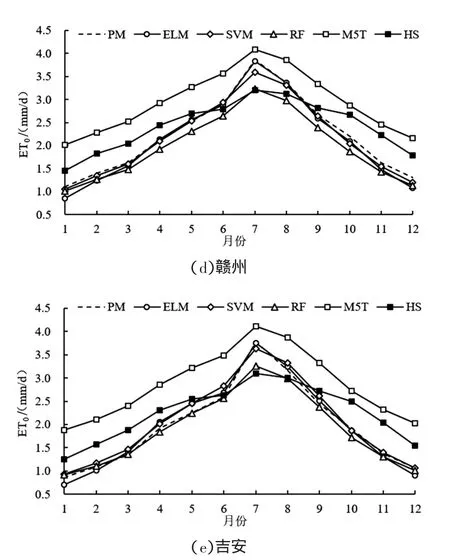
图3 不同站点不同模型模拟ET0月值精度对比

2.3 ET0模型适用性对比

表2其余站点ET0拟合结果对比为不同模型在不同站点的精度指标计算结果。由表2可以看出，由RMSE、R2和Ens组成的评价指标体系可较好地反映不同模型模拟结果的误差与一致性。ELM模型在仅有温度资料输入的前提下，RMSE仅为0.331～0.457mm/d，而 R2和 Ens分别达到了 0.945～0.969和 0.944～0.969，误差最低而一致性最高，SVM模型的计算精度次之，RMSE为0.346～0.466mm/d，而R2和Ens分别为0.941～0.969和0.939～0.966，RF模型和M5T模型的计算精度较差。机器学习模型精度均高于HS模型，根据计算得出的GPI指数可知，5种模型计算精度由高到底依次为ELM模型、SVM模型、RF模型、M5T模型、HS模型。

2.4 ET0相对误差绝对值空间对比

图4为不同模型计算值相对误差绝对值的空间分布图。由图中可以看出，不同模型在不同地区的计算精度不同。ELM模型计算精度表现为由北到南精度逐渐提高，ELM模型在南昌和南城站附近的计算精度最低，相对误差分别为17.53%和17.08%，在赣州站附近的精度最高；SVM模型与ELM模型计算精度变化范围基本一致，在南昌和南城站附近相对误差最高，分别为18.80%和18.25%；而RF模型、M5T模型和HS模型计算精度变化趋势与ELM模型和SVM模型不同，3种模型在南昌站和南城站的相对误差最低，而在吉安和景德镇附近的计算误差最高，因此在应用不同模型时，应针对站点不同选择合适的模型进行应用。

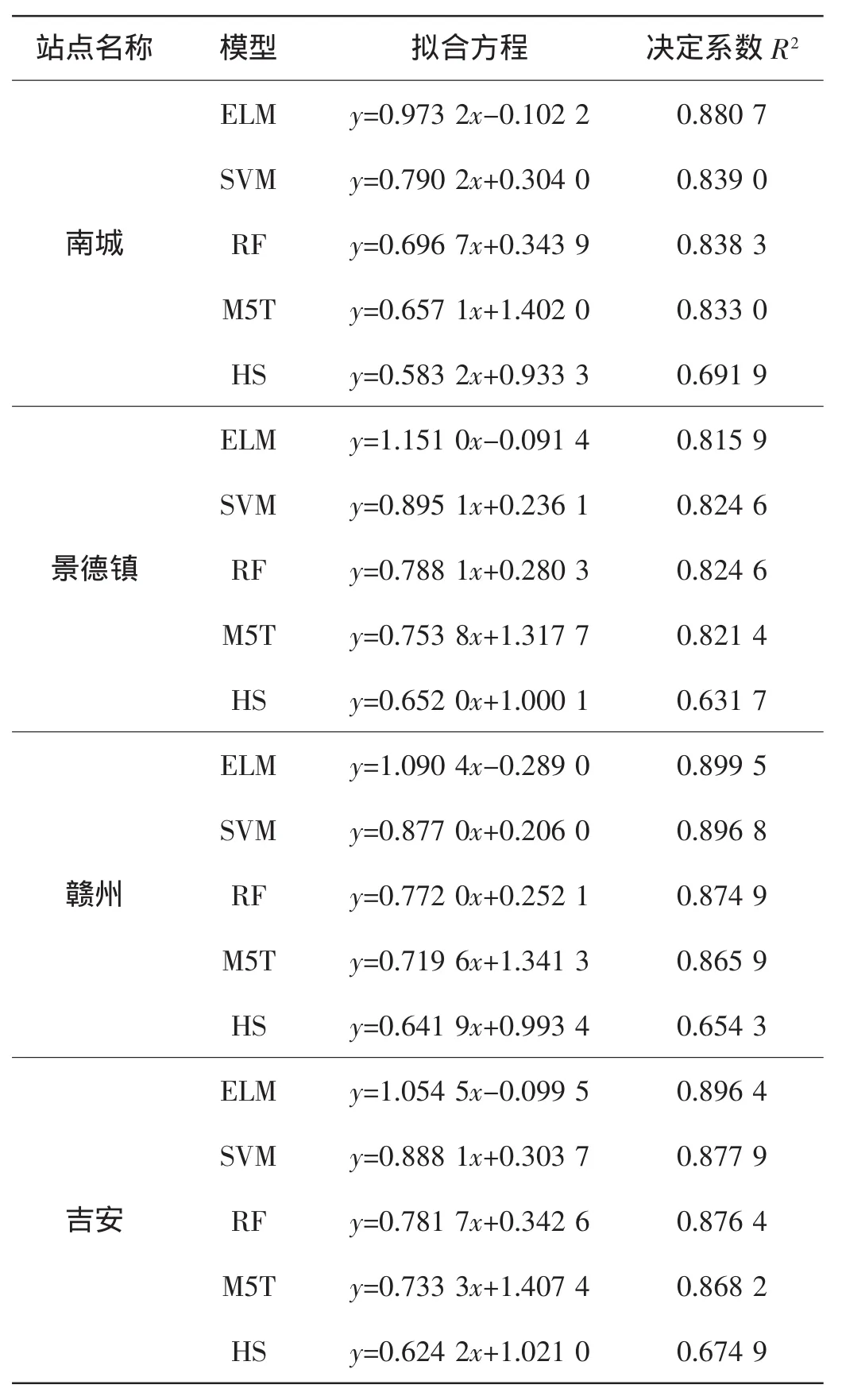
表2 其余站点ET0拟合结果对比表

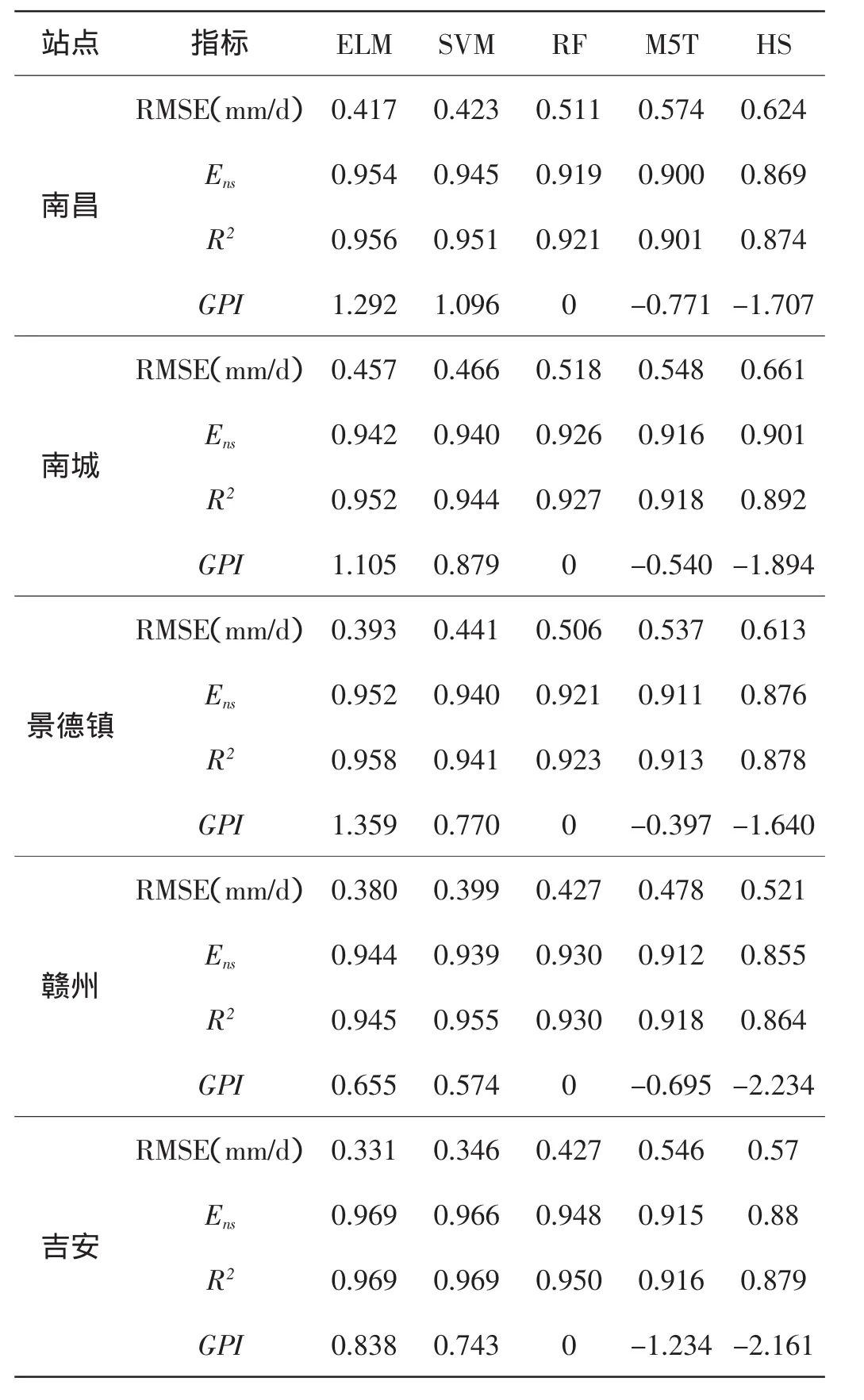
表3 不同模型计算精度指标对比表

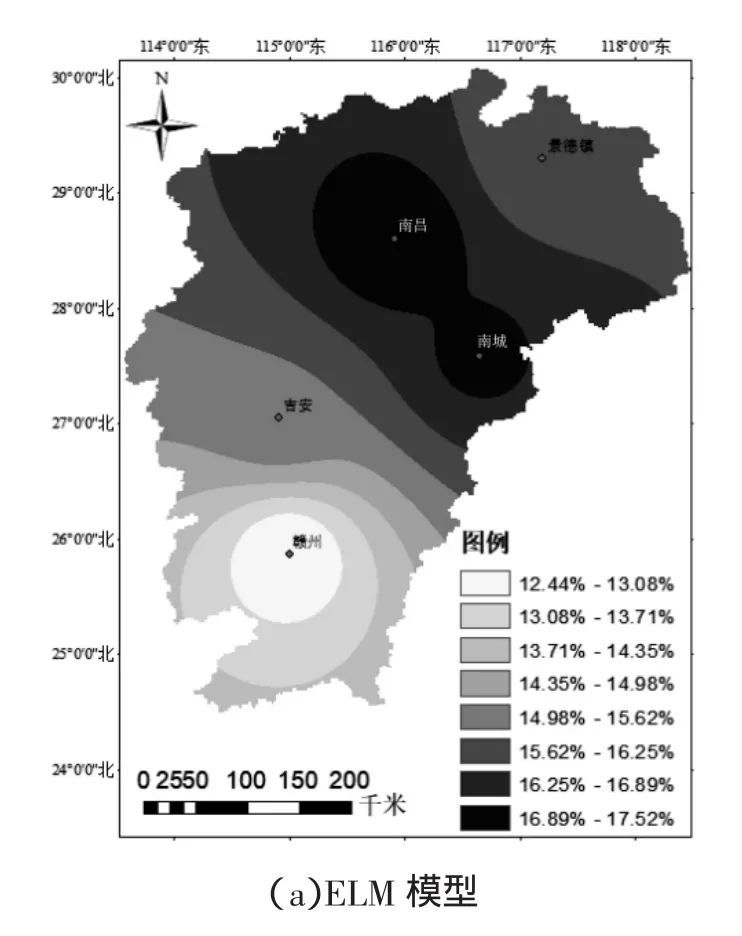
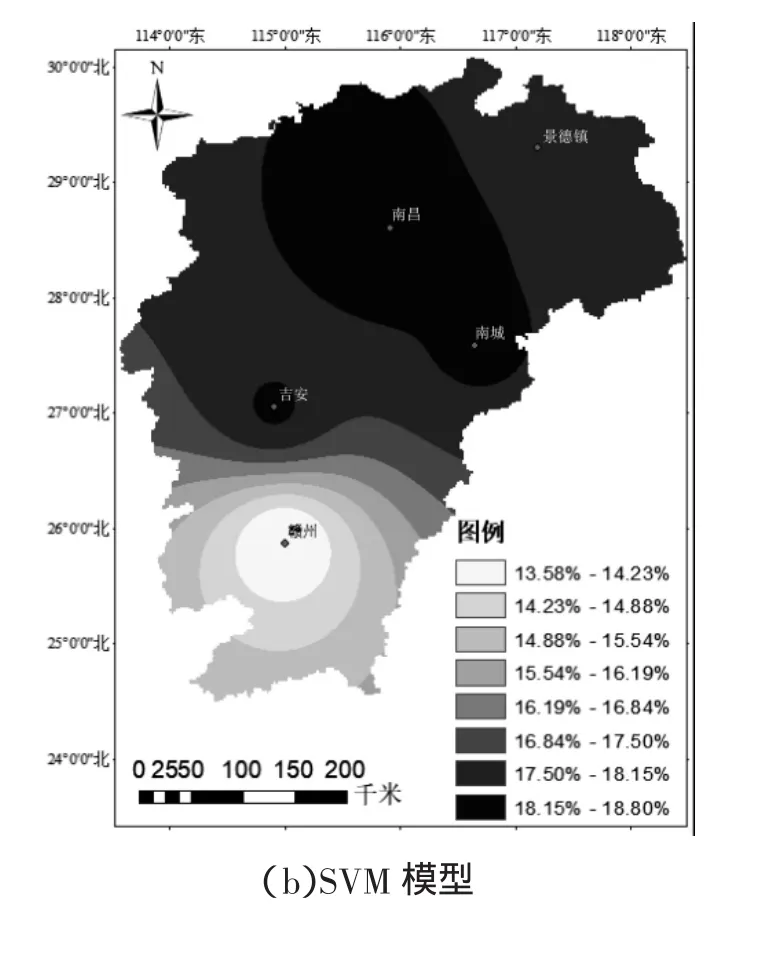
图4 不同模型ET0空间精度对比

3 结 论

通过对不同机器学习模型在仅输入温度资料条件下的ET0模拟精度对比，可得出适用于江西省计算的ET0标准模型。从日值、月值、评价指标及精度空间分布4个角度出发，综合分析了5种模型的计算精度，最终指出ELM模型在日值计算时的拟合方程斜率最好，月值计算与标准值拟合效果最好，评价指标中的RMSE最低而R2和Ens最高，表现出了最低的误差和最高的一致性，综合表明了在仅有温度资料下，ELM模型可作为江西省ET0计算的标准模型使用。