演练，触摸“学生”的认知天性

抗“疫”期间，笔者利用网上发布的各种防控讯息，创编了一组数学练习。想着在推荐学生练习之前，先让团队成员们动动脑、练练手，于是，便在微信群里发起了每日“竞答”活动。

题目一：每出门采购一次口罩，消耗家里库存1只，每次限买3只。买到了，多2只；买不到，亏1只。老张家里原有库存10只，出门10次之后，家里现有12只。请问，他有几次出门是买到口罩的？（适合三～六年级）

问题抛出后，笔者作为主持人与团队成员进行了热烈的讨论——

徐老师：应该是3次吧？

顾老师：这应该是“牛吃草”问题吧，是4次。我们可以这样进行解答。

方法一：

假设每次都买到口罩：3×10＝30（只）

相差：30－12＝18（只）

没买到的次数：18÷3＝6（次）

买到的次数：10－6＝4（次）

方法二：

假设每次都不买到口罩：10－10＝0（只）

相差：12－0＝12（只）

买到的次数：12÷3＝4（次）

验算略。

笔者：看得出，顾老师是先假设出门10次都能买到口罩，那么除去每次出门消耗掉的1只外，最后应当有30只，而实际只有12只。之所以会相差了18只，是因为其中有几次出门是没有买到口罩的，有一次没买到，现有口罩数就少了3只，这样就可算出有6次出门是没有买到口罩的，那真正买到口罩的次数就是4次。

徐老师：谢谢顾老师的启发！应该是4次。鸡兔同笼问题，差点儿错了。

本以为这个问题就这样讨论结束了，没想到于老师又在群里发声了——

于老师：是6次吧？12÷2＝6（次）。

顾老师：不是的，本来有10只。

于老师：出去买到口罩，用去1只，买到3只，实际净得2只。

笔者猜想于老师是发现了“现有12只”确实是出门买到口罩后净得的，但他把买到一次实际得到的口罩数弄错了。如果买到一次是净得“＋2只”，那出门一次没买到就该是“－1只”，所以用12 除以3才能算出买到口罩的次数。

为了激发团队成员参与“竞答”活动的积极性，最后笔者在群里作了个小结：不管结果怎样，过程都是有价值的。这也提醒我们，建模是把双刃剑，如果不把它归为某某问题，直接设x次出门买到，反而能更快捷地解决问题。

在几轮“竞答”活动结束后，笔者又把创编的十几道练习题分配给几位团队成员，让他们对这些练习题进行解析。周老师负责解析这一道“买口罩”问题，他除罗列出了假设法（类似于顾老师的解法）、列表法外，还自己命名了一种“对比法”。

对比法：读完题目，我们发现10天一共实际只买到12-10=2（只），对比下来也就相当于只有1天买到口罩，而其余的9天都做了“无用功”。这9天实际买到口罩的数量和为0，根据题目可以得到每次买到的口罩可以“抵消”掉2天亏本的口罩数量。我们可以将3天分为一组，这3天里只要是1天买到，2天没有买到算下来就总数为0。9÷（1+2）=3（组），3×2=6（次），意味着有6次没有买到，10-6=4（次），4次买到口罩。

粗略看一下，觉得还挺有道理的，但仔细一推敲，便能发现其中逻辑的混乱。第一，“10天实际只买到了2只”这种说法是不正确的。无论出门买到还是买不到，都要消耗1只，因此出门10次实际买到的口罩就是12只，或者说实际买到的比原来的库存多2只；第二，既然已经“认定”了“其余的9天都做了‘无用功’”，那还需要把这9天进行分组吗？如果将条件改成“原有库存7只”，那按照这个“对比”的思路，接下来又该怎么推演呢？

通过分析，周老师终于同意把这种“对比法”去掉，因为教师都没有能够把这种方法说清楚，那又怎么去指导学生呢？与其用一些“另类方法”去扰乱甚至误导学生的思维，倒不如用一些最为基本的方法来启发学生！

姜祈看见她的出现愣了愣，眼里光芒一闪，但很快又暗淡下去。他冷哼一声：“这个时间点，学姐不该在上课吗？”

为了进一步阐明以上观点，我建议周老师再补充一种列方程的解法。直接设出门x次是买到口罩的，根据“原来库存的只数＋买到的只数－出门10次消耗掉的只数＝现有的只数”这一关系式，列出方程“10＋3x－10＝12”。周老师看后马上回复：“如果这样的话，是不是可以有更简单的方程式？原来有10只，出门10次正好消耗10只，那最后的12只是不是就可以直接看成是买到的？那就是3x＝12，你看呢？”看得出周老师这回完全理解了题目的意思，不过笔者还是坚持原先的想法。虽然列出的方程“10＋3x－10＝12”看上去比较复杂，但它依据的关系式非常清晰，学生比较容易理解，而且适用于一般的情况。如果将条件改为“原有库存7只”，学生就很难直接找到“3x”对应的数量，而根据关系式“原来库存的只数＋买到的只数－出门10次消耗掉的只数＝现有的只数”来列方程就容易多了。所以我们不能只追求表面的“简单”，而要看这简单的背后蕴含的“道理”是不是更为一般，更具普遍性。某种程度上，只要学生能理解的“复杂”就是一种简单。至于学生能不能在“复杂”的基础上悟出更简单的方法，那就留给他们自己去探索、发现吧！

题目二：“20200202”（2020年2月2日）被称为“世界完全对称日”。你知道21世纪一共会有多少个这样的“世界完全对称日”吗？（适合五年级）

顾老师这样“竞答”：

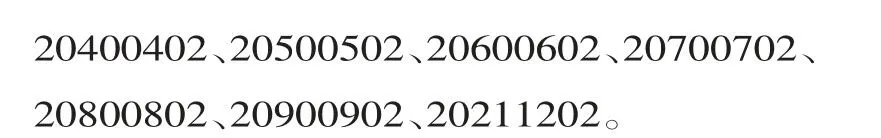
顾老师和笔者原来的想法基本是一致的，根据“世界完全对称日”的排列规律，从左往右数第5、6位表示“月份数”，因此第4位数字只能是“0”或“1”，而当第3位数字大于“2”时，第4位数字就只可能是“0”了。然后，再应用“一一列举”的策略，就能找出21世纪所有的“世界完全对称日”了。

后期在对这道题进行解析时，丁老师又带来了一种“新”的思路———

“世界完全对称日”是指公历纪年日期中数字左右完全对称的日期，如2010年1月2日（20100102），2020年2月2日（20200202）等。

“世纪”是计算年代的单位，一百年为一个世纪。21世纪一般认为是从2001年1月1日至2100年12月31日（也有不同的观点）。

先考虑20□□年，因为“世界完全对称日”的日期中数字要左右完全对称，所以就确定了4个数字：20□□□□02。这8个数字中，从左往右数，第3、4个数字表示年份的后两位，第5、6个数字表示月份。接下来，可以从表示月份的两个数字入手，也就是从1月排到12月，同时在前面补上与之对称的第3、4个数字。然后，用一一列举的策略就可以找出答案啦，它们分别是：

那么，2100年有没有“世界完全对称日”呢？答案是否定的。因为如果有的话，那得是21000012，第5、6个表示月份的数字是0、0，可是一年当中没有0月。所以，21世纪一共有12个“世界完全对称日”。

很显然，丁老师是先列举出从左往右第5、6个数字（即月份数）的所有情况：01、02……11、12，再逆推出年份数的后两位数字的。相比于笔者和顾老师的方法，虽然最终得到的12种情况并没有把年份数按顺序排列，但整体看却更为简便、快捷。笔者和顾老师把视线锁定在第3、第4个数字的特点上，而丁老师却是直接从第5、第6个数字入手，从01 开始“顺流直下”“一气呵成”。可见，无论是在学习还是在生活中，很多时候我们看问题的视角不同，获得的体验也不尽相同。多换一种角度，或许就能收获不一样的精彩。

题目三：假设一支援助医疗队由137人组成，除2名领队外，其余为医护人员。其中包括5个普通医疗队和一个重症医疗队。普通医疗队中医护人员的人数比是2∶3，重症医疗队中医护人员的人数比是1∶4。已知这支援助医疗队中共有护士93人，那么每个普通医疗队中共有医护人员多少人？每个重症医疗队呢？（适合六年级）

●方法一：严老师解答。

137-2=135（人）

5个普通医疗队医护人数比2：3

（2×5）：（3×5）=10：15

1个重症医疗队医护人数比1：4

列举法：

护士总人数重症医疗队医生人数是否是4的倍数93 15的1倍 93-15×1=78 否93 15的2倍 93-15×2=63 否93 15的3倍 93-15×3=48是93 15的4倍 93-15×4=33 否93 15的5倍 93-15×5=18 否93 15的6倍 93-15×6=3 否普通医疗队护士总人数重症医疗队护士总人数

从上表看出当普通医疗队的护士总数为15的3倍，也就是45人时，与题目相符。

所以普通医疗队的医护人员总数=45÷3×（3+2）=75（人）

每个普通医疗队的人数为75÷5=15（人）

每个重症医疗队的人数为135-75=60（人）

●方法二：顾老师的方法。

137-2=135（人）

尝试1：

假设普通医疗队共有医护人员25［（2+3）×5=25］人，则重症医疗队共有医护人员110人。

因为103比93多10人，与题目不符，所以假设不成立。

尝试2：

假设普通医疗队共有医护人员25×2=50（人），则重症医疗队共有医护人员135-50=85（人）。

因为98比95多3人，与题目不符，所以假设不成立。

尝试3：

假设普通医疗队共有医护人员25×3=75（人），则重症医疗队共有医护人员135-75=60（人）。

与题目相符，每支普通医疗队共有医护人员75÷5=15（人），每支普通医疗队共有医护人员：135-75=60（人）

两位教师都是应用假设（假设5个普通医疗队共有护士15人或5个普通医疗队有医护人员25人）、尝试的方法，最终找到答案的。“除了这些方法外，还有没有其他的方法呢？”

●方法三：严老师方程解法。

解：设重症医疗队医护人员共x人，则普通医疗队共（137-2-x）人。

每个普通医疗队共有医护人员人数=（135-60）÷5=15（人），每个重症医疗队共有医护人员135-75=60（人）。

前期在微信群里进行的这一次“演练”，让我们重新当回了一次学生，“暴露”了在面对不太熟悉的问题时自己的一些真实想法，让我们更加深刻地体会到“每个人都更喜欢在自己熟悉的领域内兜转，而只有把新知识放到更广阔的情境中才能真正有助于学习”，也使我们真正认同了“在学习中犯错误并改正错误，其实就是在搭建通往高层次学习的桥梁”这样的观点。相信这些前期积累下来的经验，将帮助我们更好地理解学生的“认知天性”，让我们接下来在与学生的网上学习互动中变得更理性、更从容。