国家创新型城市政策、高端生产性服务业集聚与地区经济高质量发展

陈 晨 张广胜

(辽宁大学 商学院，辽宁 沈阳 110036)

一、引言及文献评述

为贯彻落实习近平总书记关于“尊重科技创新的区域集聚规律，因地制宜探索差异化的创新发展路径，加快打造具有全球影响力的科技创新中心，建设若干具有强大带动力的创新型城市和区域创新中心”的重要指示，2016年科技部和发改委联合制定了《建设创新型城市工作指引》，其中明确提出“到2018年，全国若干城市进入创新型城市行列……到2020年，全国范围内更多城市进入创新型城市行列，部分城市成为具有国际影响力的创新型城市”。中国最早于2004年提出建设国家创新型城市，2008年将深圳确立为第一个国家创新型试点城市。此后，2010年确立40个城市为国家创新型城市，2011年确立了5个城市，2012年增补了3个城市，2013年又新增了10个城市，2018年4月新增了吉林、徐州等17个城市为国家创新型城市，至今共计78个城市被确立为国家创新型城市。

中国创新型城市建设是一个不断探索的过程。按《建设创新型城市工作指引》文件，其主体任务是“加强统筹规划协调，强化城市创新功能；推进城市产业升级，优化区域产业结构……”，最终细化分解成“抓改革政策落地，抓创新要素集聚，抓创新成果转化……抓创新载体建设，抓创新服务完善，抓创新投入带动，抓创新生态营造”(1)源于《建设创新型城市工作指引》，该文件来源于中华人民共和国科学技术部官方网站2016年12月1日发布的国科发创〔2016〕370号文件。，这与经济高质量发展的基本理念“创新、协调、绿色、开放和共享”不谋而合，说明了产业结构优化升级和创新驱动经济高质量发展相辅相成。而技术创新和产业升级需要有高端生产性服务业的支撑，其中高端生产性服务业由制造业分离而生，主要由金融服务、信息服务、研发及科技服务等行业构成，其产业集聚具有知识密集、技术密集、信息密集及人才密集等特性(李平 等，2017)，是驱动经济高质量发展的助推器。对现有国家创新型城市相关文献进行梳理发现，该领域相关研究较少，且主要为创新型城市的模式借鉴研究(杨小迪 等，2009)和多维指标体系下的政策城市的创新能力评估研究(邹燕，2012；周晶晶 等，2013；寇明婷 等，2014；许治 等，2016)，鲜有文献研究创新型城市政策的经济发展效果及产业作用的影响。国家创新型城市政策制定并实施已有十余年，是否促进地区经济的高质量发展呢？政策效果如何呢？在产业升级需求下，高端生产性服务业集聚能否促进创新型城市经济高质量发展呢？

通过对政府参与、支持创新以驱动经济高质量发展研究文献的梳理，相关研究文献主要集中于资源配置、营商环境构建和产业协同等几个方面，但均指出适度的政策扶持和监管才能发挥能动性，不然会阻碍经济高质量发展。政策促进论方面，财政在教育和科研经费方面支出促成要素资源的调配效应，以弥补创新资金不足(苗文龙 等，2019)；同时，改善配置扭曲问题，驱动全要素生产率提升，助推经济高质量发展(刘金全 等，2019)。创新阶段论指出，政府共担基础创新风险(葛鹏飞 等，2018)，保障应用创新的成果转化(高新雨 等，2018)，实现促创新、稳增长。此外，政策引导私人投资走向，优化投资结构(Kleer，2010)，成为制度环境建设的最佳推手(王永进 等，2018)；推动产学研的协同创新体系建设(白俊红 等，2015)；也可形成声誉效应，吸引人力、物力资源的集聚(郭景先 等，2018)，这可以促进创新产出、营商环境构建、资源结构升级，从而推进地区经济高质量发展。政策抑制论方面，首先，政策补贴挤出主体的自有创新投入(Boeing，2016；Hottenrott et al.，2017)；其次，补贴后监管不足容易导致“策略性”创新(黎文靖 等，2016)，监管过度导致主体自主能动性下降(Epstein et al.，2013)；最后，政策执行中，政策偏好、主体资源禀赋特征偏差(肖文 等，2014)及官员政绩考核的“道德风险”(陈家喜，2018)，这些都可能导致政策偏离初衷，达不到政策的最佳效率(唐书林，2016)，从而不利于地区经济高质量发展。

综上，不同学者研究政府政策参与下经济高质量发展效果的结论存在分歧，可能受困于样本选择、变量选取、实证方法等原因，但也可能受到政府政策措施差异、落实方式区别、作用主体互动关系、产业资源条件等方面的影响。众多学者指出，生产性服务业产业集聚是提高地区经济发展质量的重要路径(Martin et al.,2001；文丰安，2018；方敏 等，2019)。一方面，生产性服务业专业集聚能够提升资源配置效率(周璇 等，2019)，而协同集聚会促进知识产出和技术进步(王海宁 等，2010；熊欢欢 等，2017)，重塑价值链结构，进而推动地区经济高质量发展；另一方面，产业集聚也可能导致产业拥挤、产能盲目扩张等现象(谢波，2013；张可 等，2014)，扭曲市场竞争机制(万道侠 等，2018)，造成资源错配(程中华，2015)，从而不利经济高质量发展。由此说明，政府的支持与地区经济高质量发展息息相关，但受制于地区基础产业条件差异的影响，这就需要中央政府和地方政府协同共创，以地方资源为依托的政策执行，可实现区域经济发展质量的提升。

综上，现有研究中，政府差异化政策对地区经济高质量发展作用效果并未达成共识，对产业资源效应的影响机制探讨不足，尤其对于国家创新型城市政策经济效果研究缺失。考虑国家创新型城市建设中“地方试点-中央总结-地方推广”(李政 等，2019)的特点，本文贡献体现为：第一，基于创新驱动经济发展质量提升的现实需求，研究创新型城市政策对经济高质量发展的作用效果，丰富了科技创新政策相关方面的研究；第二，在政策执行的影响因素上，考虑到产业结构形态对政策执行效果的影响，为后续政策执行过程中保障性措施的制定提供理论依据；第三，依据国家创新型城市分批次落实的特性，在研究方法上采用渐进双重差分模型拟合现实情况，避免了样本选择的内生性问题。

二、研究设计

(一)模型构建

影响城市经济发展质量的因素众多，被确立为创新型试点城市后的经济发展质量提升可能并非政策作用，而是内部资源、外部环境以及宏观经济形势变动的结果，因此，本文使用双重差分法来处理数据。双重差分法可以通过对处理组与对照组政策实施前后的两次差分，去除掉不随政策时间变化和其他外部非可控因素对企业创新绩效的影响，从而估计出政策实施对创新型城市政策和城市经济质量的净影响，使得结果较为稳健。

1.渐进性差分模型

基本的双重差分模型中，政策实施时间为单一时点，但国家创新型城市则是分批次逐渐推广的，因此构成渐进性双重差分模型，如Kudamatsu(2012)、Almond et al.(2013)和Wang(2013)的研究中均采用过此种方法。本文借鉴郭峰等(2018)的处理方式，构建渐进性双重差分模型如下：

malit=β0+β1treatedit+β2trendit+β3Controlit+εit

(1)

其中，malit反映城市的经济发展质量；treatedit反映若i城市t年被确立为国家创新型城市，在确立的当年和此后各年treatedit=1，否则treatedit=0，t为数据报告年份，此种设置方式可以避免原有的双重差分模型的处理方式，即将变量分为是否为处理组变量、政策时间前后变量及两者交乘项，而直接以单一变量表示政策差分变量，这更为直观地体现出政策逐渐实施的过程；trendit的处理方式为，若t>si，则trendit=t-si，否则trendit=0，si表示城市i被确立为国家创新型城市的具体年份，该变量经过此种方法处理之后，表示城市被确立为国家创新型城市的“年龄”，通过与被解释变量回归，可以反映出试点年龄对企业创新绩效或企业价值增长趋势的影响；Controlit为控制变量。

2.固定效应渐进双重差分模型

国家创新型城市的选取并不完全随机，这可以避免双重差分模型中基本的准自然实验假设存在的偏差，以及处理组与对照组变量可能存在内生选择性偏误。若科技部基于可控因素确立国家创新型城市，即可直接在双重差分模型中控制该因素；若基于不可观测因素确立试点城市，则可以将基本渐进双重差分模型中随机项分解为固定效应(αi)和时变误差(μit)两个部分。借鉴王智波等(2018)的方法，构建如下的固定效应渐进双重差分模型(2)本文这样使用固定效应渐进双重差分模型是由于建立在双固定效应模型的基础上，即通过增加渐进双重差分虚拟变量项，以控制非时变误差造成的内生性影响，这样与双固定效应模型的作用效果一致。：

malit=β0+β1treatedit+β2trendit+β3Controlit+αi+μit

(2)

3.处理效应渐进双重差分模型

Maddala(1983)对Heckman(1979)的修正选择性偏误模型应用到政策评价研究中，会衍生出干预效应双重差分模型。本文借鉴Maddala(1983)和王智波等(2018)的处理方式，构建处理效应渐进双重差分模型。

主回归模型：

malit=β0+β1treatedit+β2trendit+β3Controlit+εit

(3)

样本模型：

(4)

(二)变量说明

1.被解释变量(mal)

现有对经济发展质量量化的方法主要有两种：其一为构建指标评价体系的度量方式；其二为对全要素生产率的方式加以量化，具体包括回归残差提取法和数据包络分析法。鉴于效率的度量和经济发展质量增长趋势的研究，基于DEA-Malmquist指数方法可以计算出城市经济发展质量指标。其中，投入要素指标涉及劳动力、资本存量、知识投入，产出要素指标指的是城市的实际GDP产出值。

(1)投入指标。一是劳动力投入，本文采用各个城市的年末就业人员总量加以衡量。二是资本存量投入，本文选取各个地级市的年末社会固定资产投资总额来表示，同时以2003年为基年，采用永续盘存法予以估算各个后续年度的资本存量指标，其计算公式为：ki,t=(1-δ)Ki,t-1+Ii,t。其中，K表示前期积累的资本存量；I表示今年增社会固定资产投资；i和t表示城市和年份；δ表示固定资产折旧率，参照单豪杰(2008)的处理方法，将其资本折旧率设定为10.96%。三是知识投入，根据保罗·罗默的内生增长经济理论，经济发展的内生驱动发展因素除了人力资本与物质资本外，知识资本投入的作用也不容忽视，这也是索洛余值中知识贡献的作用，因此，选取各个地级市政府各年教育财政支出金额指标衡量知识投入对各地产出的影响，从而测度其对各地区城市经济增长与环境技术变革的作用。

(2)产出指标。产出指标用各城市的地区生产总值表示。为了去除各年GDP增长中包含的价格波动影响，同时也考虑到增长的连续性，本文以2003年为基年，用各地区各年的地区生产值增长指数对GDP进行调整，最终得到各地实际经济产出值。

2.解释变量(treated、trend)

本文研究城市被确立国家创新型城市后经济发展质量出现的变化，因此以政策性虚拟变量作为解释变量。依据上述模型中变量的含义，城市政策的差分变量为treated，确立为国家创新型城市的“年龄”变量为trend。

3.调节变量

(1)产业集聚指数(sagg)。本文产业变量主要指专业化集聚指数，借鉴于斌斌(2018)的区位熵做法，具体的计算公式为： sagg=Max(sij/si)。其中，sij为i城市中行业j的就业人数占该城市总就业人数的比重，而si为所有城市行业j的就业人数占全国城市就业人数的比重。因而，上述两项指标的数值越大，代表各个产业的集聚水平越高，反之则越低。

鉴于现阶段中国产业结构仍处于逐步调整时期，第二产业产值在国民经济产值中的比重逐渐下降，而第三产业产值比重在逐步提升，第三产业对经济发展质量提升又主要依靠生产性服务业的推动，其中高端生产性服务业(3)高端生产性服务业主要包括：信息传输、计算机服务业和软件业；金融业；租赁和商业服务业；科学研究、技术服务和地质勘查业。的作用尤为突出。因而，本文研究高端生产性服务业集聚对城市经济高质量发展的推动作用。

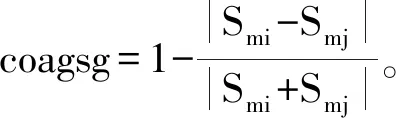
4.控制变量

(1)政府干预程度(gov)。在市场经济起到基础性作用情况下，政府的过度干预会导致城市活力受限，经济发展动力不足；但同时，政府的干预也保证了经济秩序的稳定，良好的经济环境。因此，政府干预对经济发展质量的影响作用有待验证。本文主要用财政支出与地区生产总值之比对政府干预程度变量加以量化。

(2)交通发达程度(tran)。城市交通越发达，物流传输更为便捷，这有助于加强各主体的沟通交流，对经济的发展速度和质量将产生变革性作用。本文以人均道路面积为指标，对各城市的交通发达程度加以量化。

(3)资金闲置率(dep)。城市的储蓄量越大，表明资金闲置率越高，资金配置出现失调，这不利于经济产出最大化，对区域经济发展质量起到负向作用。本文采用地区金融机构存款余额与地区生产总值之比衡量该变量，指标值越大，表明资金闲置率越高。

(4)居民生活水平(dev)。城市居民生活水平越高，消费能力越强，从而有助于扩大内外部需求，刺激地方经济增长。本文选取地区人均生产总值度量居民生活水平。

(5)城市规模(scale)。城市人口的集聚过程，也是资源集聚的过程，从而使得城市规模扩大，此时城市基础资源更丰富，机会更多，更利于区域经济发展质量的提升。本文采用2014年国务院调整城市规模划分标准，将样本数据选取的城市划分六个等级，由此变量赋予1～6的数值(4)2014年国务院调整城市规模划分标准，以城市人口数量作为划分城市规模依据。将城市人口超过1000万的城市认定为超大城市，赋值为6；将城市人口数量在500万至1000万之间的城市认定为特大城市，赋值为5；将城市人口在100万与500万之间的城市认定为大城市，其中人口数量在300万至500万之间的城市，赋值为4，人口数量在100万至300万之间的城市，赋值为3；将城市人口数量在50万到100万之间的城市认定为中等城市，赋值为2；将城市人口数量低于50万的城市认定为小城市，赋值为1。，数值越大表明城市规模越大。

(6)研发投入(rd)。在创新驱动战略引领下，政府在科技创新研发中投入的力度越大，说明对科技创新越重视，对经济发展质量的提升作用就越强。因此，本文以科技支出占地区生产总值的比重来测度研发投入，验证研发投入对城市经济发展质量的影响。

(三)数据来源及描述性统计分析

鉴于首个国家创新型城市设立在2008年，同时兼顾数据的可获得性，本文数据来源于2005—2017年《中国城市统计年鉴》《中国城市建设统计年鉴》《中国统计年鉴》和部分省份统计年鉴。截至2016年，中国共计设立了298个地级及以上级别城市，但由于2005—2017年国家对部分城市进行了行政区划调整，同时部分城市数据严重缺失，最终本文整理得到285个地级及以上级别城市样本数据，将其中国家创新型城市作为处理组，非国家创新型城市作为对照组样本。其他年份样本存在数据缺失的情况，本文采用本地区前后两年指标数值之和再平均后的数值予以添补。

由表1变量描述性统计结果看出，各个城市主体经济发展质量差异较大，大部分城市还处于经济低质量发展阶段，个别城市出现离群值，经济发展质量要显著高于平均水平。城市间的高端生产性服务业集聚同样存在显著差异，从平均值来看，城市整体处于低集聚水平，仅部分竞争力较强的城市地区集聚指数处于高水平，与经济发展质量相近。各城市间生产性服务业与制造业协同集聚水平差距较小，但通过最大值与最小值取值可以看出，各个城市协同集聚指数均很小，说明中国各城市不同产业的协同发展水平比较均衡，但还处于低度协同阶段，不能满足经济高质量发展的提升要求。

三、实证结果及分析

(一)双重差分模型的适用性检验

使用双重差分模型主要为了排除政策变量外的其他因素变动的影响，其使用要满足两项基本假定：一是确定国家创新型城市的选定是随机的，与城市前期经济发展质量不存在直接关系，即满足政策的外生性，符合反向因果假定；二是被确立为国家创新城市的处理组与对照组在政策实施前的经济发展质量变化趋势基本一致，即满足平行趋势假定。

1.反向因果检验

科技部联合发改委分批次确立国家创新型城市，主要是参考地区基础资源、研究机构、创新机制及环境设施等因素，而不是仅以地区经济发展状况为考核指标，这初步符合双重差分模型的外生性要求。但鉴于国家创新型城市政策是在10年内分批依次确立的，政府部门可能会在经济基础相对较好的城市先试点运行，再将范围逐步扩大，因此模型的适用性不能仅基于主观判断，还需要构建模型进行实证验证。本文借鉴郑新业等(2011)、王小龙等(2015)、郭峰等(2018)、朱晓文等(2019)的处理方法，采用Logit模型检验试点企业政策的外生性条件，具体模型如下：

Logit(treatedit)=α0+α1Perfomance(L.malit)+α2L.Controlit+εit

(5)

其中，城市经济发展质量和控制变量分别选取了其一期滞后值，以考察前期的经济基础和城市资源条件是否影响试点城市的确立。若前期的城市经济发展质量与政策变量在Logit回归后系数不显著，则说明前期经济发展质量与是否确立为国家创新型城市不相关，满足政策模型设定的外生性假设要求。

国家创新型城市从2008年开始，在2010年、2011年、2012年、2013年和2018年分六批依次设立相应城市为国家创新型城市，但考虑到统计数据的滞后性，2018年确立的城市很难搜集到政策实施后的样本数据，因而将2018年设立的城市仅作为对照组，将前期设立城市分为五个批次选取处理组和对照组，并进行分批次回归检验。首先，将2008年确立的深圳作为第一批的处理组，其后设立的城市作为深圳的对照组；其次，将2010年确立的北京等40个城市作为第二批的处理组，2010年以后设立城市作为第二批的对照组；以此类推，将2011年确立的秦皇岛等5个城市作为第三批的处理组，2011年以后确立的城市作为第三批的对照组；将2012年设立的南通等3个城市作为第四批的处理组，之后设立的城市作为第四批的对照组；最后，将2013年确立的泰州等12个城市作为第五批的处理组，2018年设立的徐州等17个城市作为第五批的对照组，并进行Logit反向因果回归检验。结果如表2所示。

表2中Logit回归结果显示，第一批次国家创新型城市经济发展质量与政策差分变量的分组回归系数均不显著；其他四个批次组别回归中，系数同第一组系数一样不显著。说明区域经济发展质量并非城市被确立为国家创新型城市的决定因素，本文选取的样本数据满足渐进性双重差分的外生性假设条件。控制变量中，城市地区交通信息发达程度和金融发展程度对城市确立为国家创新城市存在一定影响，说明了地区基础资源条件优良有利于国家创新城市的确立，也与科技部确立创新型城市的现实情况相吻合。

表2 城市经济发展质量与政策选取的反向因果检验

注：(1)为考察前期的经济基础和城市资源条件对试点城市确立的影响，加入了变量inf、consume、level。其中，inf表示各城市的信息化水平；consume表示各城市社会消费品总额与GDP比值；level表示各城市的城市等级，当城市为直辖市赋值为4，副省会级城市赋值为3，其他省会赋值为2，一般地级市赋值为1。(2)***、**、*分别代表在1%、5%、10%的水平上显著，估计系数下括号内的报告数值为经过异方差稳健标注调整的t统计量值，下表同。

2.平行趋势检验

双重差分模型的另一个前提假设为平行趋势假设，即处理组与对照组在政策实施之前不存在显著的系统性差异，或两者的差异不随时间变化。本文借鉴Galiani et al.(2005)、王小龙等(2015)、郭峰等(2018)、朱晓文等(2019)的处理方法，构造包含时间哑变量在内的回归模型：

(6)

其中，d_j为政策实施前时间哑变量，表示城市被确立为国家创新型城市前的年数，将该虚拟变量与政策实施差分变量交乘，若政策实施前处理组与对照组变量不存在显著差异或差异固定，则交乘项系数应不显著。与反向因果检验类似，分批次进行分组回归检验。由于最早的深圳在2008年被确立为国家创新型城市，因此第一批次有四期交乘回归系数影响；第二批处理后出现政策实施前六年交乘项；第三批处理后出现政策实施前七年交乘项；第四批企业处理后出现政策实施前八年交乘项；最晚确立的第五批国家创新型城市，有九期受时间哑变量交乘项影响，最终平行趋势检验结果如表3所示。

表3结果显示，第一批及第五批平行趋势检验中，政策实施前时间哑变量与政策差分交乘项的回归系数显著，而第二批、第三批和第四批城市的交乘项回归系数并不显著。仅交乘项系数不显著，说明政策实施前处理组和对照组不存在显著差异。而第一批与第五批次系数显著，说明政策实施前处理组与对照组本身存在差异。但第一批处理组城市仅有深圳1个，第五批处理组城市有12个，其样本量较小；而第二批至第四批处理组城市共计48个，占全部国家创新型城市的80%。表3中列(6)全样本的平行趋势检验并未考虑不同城市政策实施时间节点的差异状况，而将所有享受政策城市作为处理组，其他城市作为对照组，回归结果显示大部分回归系数并不显著，只有个别系数显著。此外，本文对平行趋势检验中模型的交乘项系数进行了联合显著性检验，其F值检验结果与各项系数的回归结果类似。由此，说明国家创新型城市的经济发展质量在被确立前与非国家创新型城市不存在显著差异，满足双重差分模型的平行趋势假定。

表3 城市经济发展质量平行趋势检验

表4 试点城市政策实施后经济发展质量效果检验

平行趋势检验是为保证处理组和对照组城市在政策实施前经济发展质量不存在显著差异时形成对比。而本文对模型进行扩展，加入了政策实施后趋势检验，以分析政策实施后处理组和对照组是否存在显著差异，为后续政策效果评估做铺垫，具体结果如表4所示。

为此，构建政策实施后时间虚拟哑变量dj，当城市被确立为国家创新型城市后的第j年，则dj=1，否则dj=0。为与表3形成对比，表4中列(1)—(6)分别为第一批至第五批城市及全样本的政策实施后效果。从回归系数可以看出，6列结果的交乘项系数均显著为正，说明国家创新型城市政策实后，其经济发展质量得到显著提升。

(二)经济高质量发展基本分析

鉴于政策分批次执行的事实，本文采用渐进性双重差分模型分析国家创新型城市的经济发展质量效果。考虑到政策确定的样本存在选择偏误，可以将基本渐进性双重差分模型扩展至固定效应双重差分模型，从而与处理效应双重差分模型形成对比，具体结果如表5所示。

表5 国家创新型城市政策对城市经济发展质量作用效果

表5中列(1)、(4)和(7)展示了政策对经济发展质量的基本效果，列(2)、(3)、(5)、(6)和(8)不仅包含政策的基本效果，还列示了政策实施的趋势效果。其中，列(1)—(3)主要采用基本的渐进双重差分模型，列(4)—(6)采用固定效应双重差分模型，列(7)—(8)采用处理效应双重差分模型。列(1)、(4)和(7)的政策差分变量回归系数均在1%的显著性水平上为正，说明被确立为国家创新型城市后，其经济发展质量得到显著提升。其余列的政策差分变量及政策实施年龄变量的回归系数大体均在1%的显著性水平上为正。说明创新驱动促进了地区经济发展质量的提升，且在政策制度保障下，不仅在短期内促进城市经济发展质量提升，还改变了城市经济发展质量增长趋势。在控制了城市基础条件变量后，回归系数同样显著，说明地区基础资源优良，与政策作用协同，从而显著促进地区经济高质量发展。对比三种模型的系数大小，处理效应渐进差分模型下系数为0.156，大于固定效应渐进差分模型系数0.023，也大于渐进双重差分模型系数0.012，rho值为负，p值为0，说明处理效应模型设置合理，前述模型显著低估了政策对区域经济发展质量的提升作用；在更好地控制内生变量后，政策作用效果也更为显著。

(三)经济高质量发展的长期效应分析

国家创新型城市政策实施后，城市将吸引更多的优秀人才，集聚更多的资金，促进地区经济发展。但政策在实施后，科技部还定期对城市的创新绩效进行评估，官员可能为在位期间的政绩而产生寻租行为，短期内出现“敷衍性”现象，官员在位期间看似出现经济增长，但对地区经济发展质量长期会产生负向影响(涂远博 等，2018)。因此，在了解政策实施基本效果后，可以通过模型变量的设定，以关注长期内每年的政策实施效果。

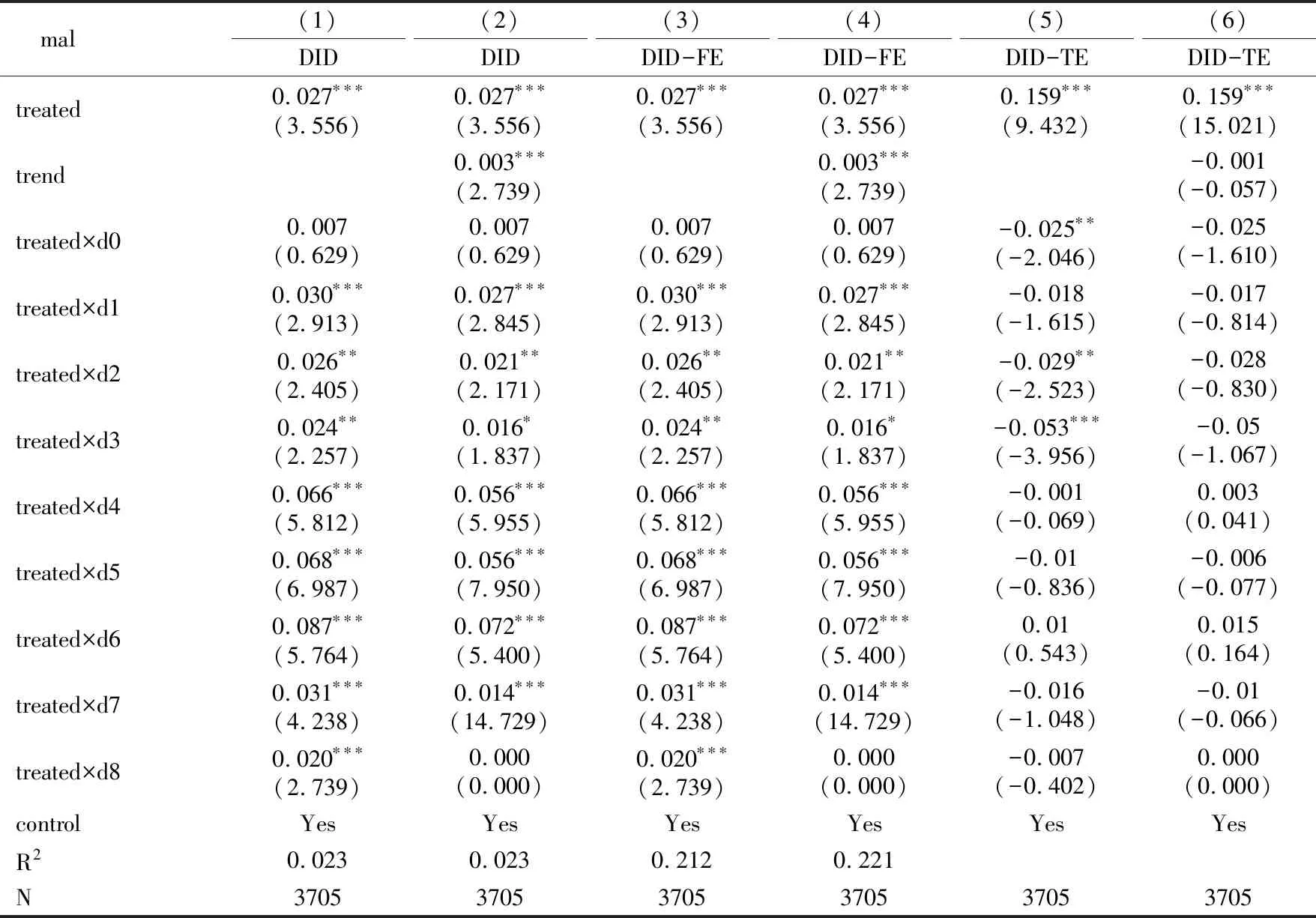
表6 国家创新型城市政策对区域经济发展质量的长期效应分析

借鉴Beck et al.(2010)的处理方法，构建政策实施后多个时期的虚拟变量dj，将政策实施后j时期的虚拟变量dj与政策差分项treated进行交乘后，再放入模型中与城市经济发展质量变量回归，验证政策实施后j年内对区域经济发展质量的每年影响效果。其中，当城市被确立为国家创新型城市后的第j年时，dj=1，否则dj=0。最终，政策实施对地区经济发展质量长期效应结果如表6所示。三种模型六列回归结果的政策时间虚拟变量与政策差分变量的交乘项回归系数均显著为正，说明政策对地区经济产生叠加的促进作用。比较八年中回归系数的大小，在被确立为国家创新型城市的前六年，区域经济发展质量呈现逐年增长趋势，在第六年政策对经济高质量发展的作用效果最强，回归系数达到最大值0.087。其后又因政策存在时效性，回归系数逐渐减少。说明国家创新型城市政策在区域经济高质量发展中呈现长期叠加效应，且治理质量对提升高质量效应作用更大，但政策存在时效性，在六年后对经济发展质量的影响逐渐减弱。因此，国家创新型城市的确立能够在长期内对地区经济的高质量发展产生促进作用，但政策效果呈现倒U形结构，会出现政策效果拐点，政策资源的扶持应在政策确立后的六年内逐渐增大，以求达到政策效果最大值，否则资源配置会失调，将造成资源的浪费。鉴于数据的可获得性，仅能得到政策实施后八年的效果评价值，政策效果的时效期还有待后续长期跟踪研究。

(四)稳健性检验

1.替换被解释变量

本文基于DEA-Malquist指数法下测算的经济发展质量(mal)作为被解释变量指标，替换为地区经济发展水平指标(gdp)，以地区生产总值加以量化，重新进行回归，结果见表7。与基本回归结果类似，被确立为国家创新型城市对地区经济生产总值产生正向影响。trend回归系数在1%显著性水平下为正，说明被确立为创新型城市能够提高地区经济发展水平的增长趋势。与前述回归结果一致，结论稳健。

表7 国家创新型城市政策对地区生产总值的影响

2.倾向匹配得分法

前述的研究采用是否为国家创新型城市的方式设置处理组与对照组，但这容易产生系统误差。在此，通过倾向匹配得分的方法，选取政府干预程度、人力资本水平、居民生活水平、外商投资水平、信息化程度、交通发达程度、研发投入、金融发展水平、居民消费水平、人口密度等指标作为样本的匹配变量，采用半径匹配的方式，为78个处理组中的国家创新型城市匹配对照组样本，最终获得974个处理组样本，2706个对照组样本，共计3680个样本。采用PSM-DID重新进行回归，结果见表8。与基本回归结果一致，被确立为国家创新型城市后显著提升地区经济发展质量，并对经济发展质量提升具有增长趋势效应，本文研究结论稳健。

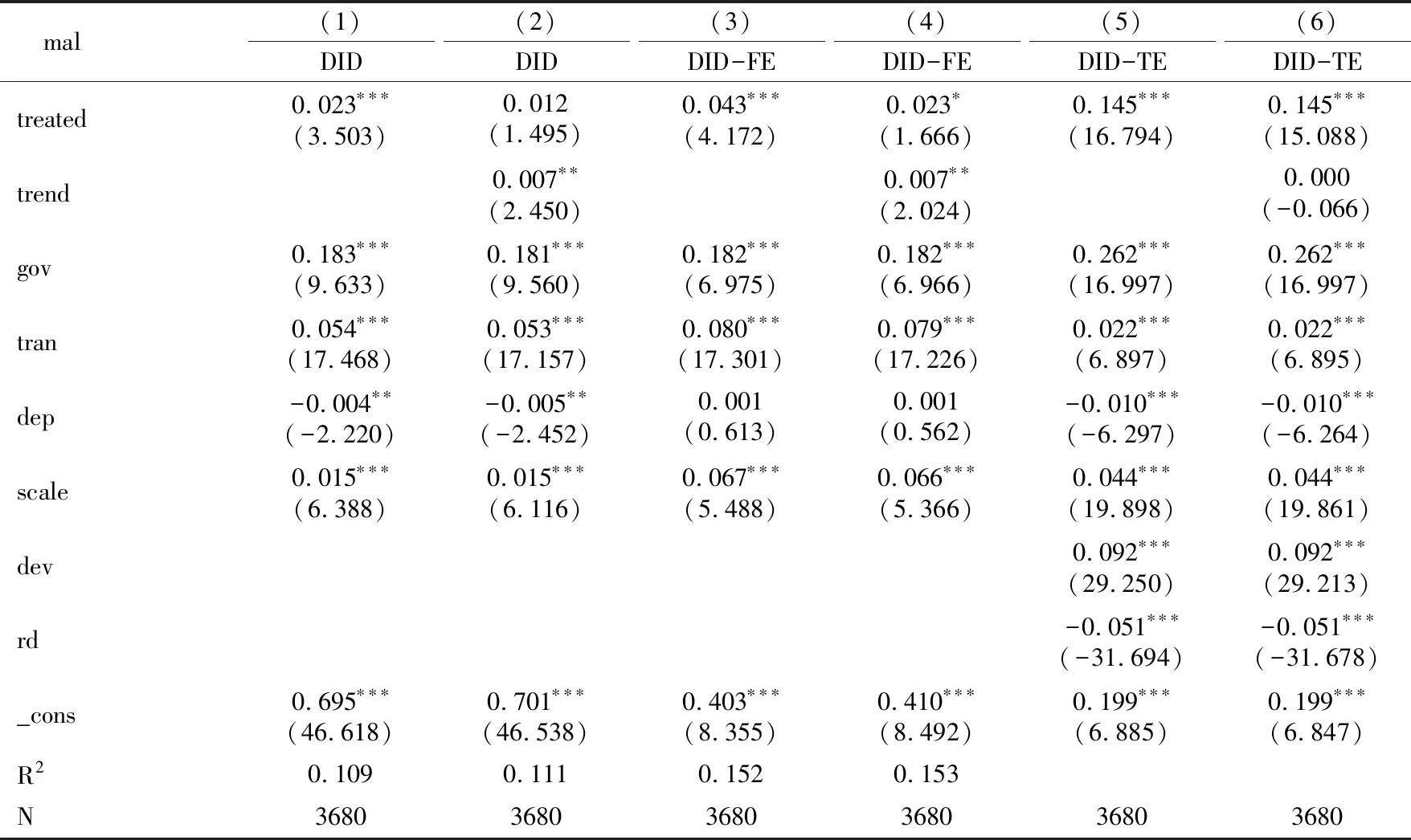
表8 倾向匹配得分法下国家创新型城市对地区经济发展质量影响分析

3.安慰剂检验

使用双重差分模型，主要是通过设定政策和时间两种类型的虚拟变量，然后将两变量交乘，将三者同时放入回归模型进行回归分析。但模型设定后的回归系数较为显著，可能存在变量形式设定导致的因变量虚假回归的结果。为尽量减少此种回归偏差的出现，本文采用安慰剂检验的虚假因变量进行检验，在政策变量设定不变的情况下，可以检验政策变量对非政策影响因素回归结果是否同样显著，若回归系数显著，说明前述回归结果可能存在虚假现象，若回归系数不显著，表明前述回归结果稳健。

为排除内生性问题，选取城市的生态环境质量(male)作为被解释变量，以替换掉经济发展质量(mal)指标重新进行回归，结果见表9。除固定效应双重差分模型外，政策差分变量在5%显著性下显著外，其余回归模型结果均不显著。由此，国家创新型城市设立仅对受政策影响的经济发展质量产生正向促进作用，对非政策影响因素不产生影响，本文研究结论稳健。

表9 虚假因变量回归

四、高端生产性服务业集聚作用分析

为追求经济的高质量发展，需转变现有产业结构模式，即由第二产业为主导模式逐渐向第三产业为主导的结构模式过渡。第三产业中，对经济发展质量提升功效最大为生产性服务业，尤其是高端生产性服务业。鉴于高端生产性服务业的产业特性，其是科技创新和经济高质量发展的支柱性产业，为城市发展带来资金和技术支持。因此，在创新驱动发展战略指引下，本文研究高端生产性服务业集聚形式差异，以区分国家创新型城市政策对区域经济发展质量的影响。

(一)高端生产性服务业专业化集聚的作用分析

鉴于现阶段产业发展呈集聚状态的现实，高端生产性服务业专业化集聚为地区经济发展提供更多的机会与可能，高端生产性服务业专业集聚会产生显著的知识溢出效应，加快信息的流动速度，提升经济产出效率，促进地区经济的高质量发展。但高端生产性服务业的专业集聚又会因企业过多，造成资源配置不合理，恶性竞争下出现资源的浪费，产生拥塞效应，对地区科技创新产出和经济发展质量造成损害。国家创新型城市政策实施后，城市将获取更多的资源，高端生产性服务业专业化集聚在政策导向下对区域经济发展质量的影响会产生何种作用呢？本文通过构造高端生产性服务业专业化集聚指数与政策差分项的交乘项以进行回归验证，结果如表10所示。

表10 高端生产性服务业专业化集聚对政策效果的调节作用

表10中,列(1)、(3)、(5)、(7)展示了高端生产性服务业专业化集聚在国家创新型城市政策对区域经济发展质量影响中的调节作用；列(2)、(4)、(6)、(8)展示了高端生产性服务业专业化集聚在国家创新型城市政策对区域经济发展量增长趋势中的调节作用。其中，列(1)、(2)是基本渐进差分模型结果，列(3)、(4)是固定效应渐进双重差分模型结果，列(5)—(8)是处理效应渐进双重差分模型结果。结果显示，高端生产性服务业集聚与政策差分变量交乘项系数在三种模型下均显著为正。说明高端生产性服务业专业化集聚能够为研发创新和经济活动提供更多便利条件，对政策实施下地区经济的高质量发展具有促进作用。高端生产性服务业专业化集聚与政策实施下经济增长趋势的交乘项的回归系数为正，但不显著，说明高端生产性服务业专业化集聚对区域经济发展质量提升的长期效果并未显现。可能是由于：中国还处于产业结构调整转型的初级阶段，第三产业对经济发展的作用在逐渐提升，但生产性服务业，尤其是高端生产性服务业产业的竞争力的提升并非一蹴而就的，需逐渐累积叠加。因此，中国高端生产性服务业核心能力不足，虽然能够促进地区经济发展，但长期效应未能发挥，后期各城市应注意高端生产性服务业的集聚竞争力建设，为区域经济长期高质量发展提供动力。

(二)高端生产性服务业与制造业协同集聚的作用分析

产业的专业化集聚主要考虑的是产业间的水平联系，而产业的协同集聚注重产业间的垂直互动关系。产业协同集聚以产业链的融合发展为目的，从而实现资源的自主配给供应，减少信息挖掘和交流成本，最终呈现显著的正外部性。鉴于现阶段高端生产性服务业核心能力建设仍在逐步进行，与制造业的协同发展与集聚程度并不高，高端生产性服务业与制造业的协同集聚仅表现为两种产业简单的“集中”分布效应，对区域经济发展质量作用并不显著；是否已经实现了产业间的“聚合”效应，对区域创新和经济的高质量发展是否起到显著促进作用，这需要对集聚程度测算进行验证分析，结果如表11所示。

表11 高端生产性服务业与制造业协同集聚对政策效果的调节作用

表11结果显示，在三种渐进双重差分模型下，高端生产性服务业、制造业协同集聚与国家创新型城市政策差分变量的交乘项系数均在10%的显著性水平下为正，且此交乘项系数值比表10中交乘项系数值要更大，说明高端生产性服务业与制造业协同集聚比高端生产性服务业专业化集聚对国家创新型城市经济高质量发展的促进作用要更强。而高端生产性服务业与制造业协同集聚对国家创新型城市经济发展质量的增长趋势作用交乘项系数并不显著，与高端生产性服务业专业化集聚的作用效果类似。由此说明，高端生产性服务业与制造业产业间的垂直互动关系，能够对区域经济高质量发展起到协同作用，而较单一产业的溢出效应要更大。但各个城市间产业结构发展不均衡，大部分城市高端生产性服务业储能不足，无法满足区域经济高质量发展下的集聚需求，长期内没有充分发挥其应有的作用，这需在城市后期建设中协调完善。

五、结论与启示

考虑数据的可获得性和国家创新型城市分批次设立的特性，本文选取2004—2016年285个城市的样本数据，将前五个批次确立的61个国家创新型城市作为处理组，采用渐进双重差分模型验证被确立为国家创新型城市后区域经济发展质量的变化情况。研究结果表明：被确立为国家创新型城市显著促进地区经济发展质量的提升，且显著提升地区经济发展质量的增长趋势；创新型城市政策实施后能在长期内促进地区经济发展，但政策效果存在时效性，在1～6年内对经济发展的效果呈现逐渐增强的趋势，但6年之后效果逐渐减弱；各城市高端生产性服务业发展对政策作用效果起到正向调节作用，高端生产性服务业与制造业协同集聚效果强于高端生产性服务业专业化集聚，说明产业间的垂直互补集聚效应大于单一产业的水平效应；但高端生产性服务业与制造业协同集聚及高端生产性服务业专业化集聚对国家创新型城市经济发展质量的增长趋势影响都不显著。

国家创新型城市政策推动地区经济的高质量发展，但存在时效性；地区产业集聚在其中起到正向调节作用，但因中国产业结构仍需不断调整，大部分城市的高端生产性服务业集聚状态未能满足经济发展质量需求，对经济高质量发展的长期增长趋势效应的影响并不显著。鉴于此，提出以下政策建议：

(1)要有序推进国家创新型城市政策的试点范围，推动中国创新驱动经济高质量发展战略的实现。城市是中国经济发展的主要功能主体，城市经济发展质量的提升，才能带动中国经济的大踏步向前发展，实现经济的高质量发展。城市被确立为国家创新型城市后，基于政府政策的支持及声誉机制下人才资金的集聚，地区经济发展质量将得到显著提升。因此，在中央政府领导下，因地制宜设立推广试点城市范围，以实现2020年创新型城市的建设目标，进而助推中国经济竞争力提升。

(2)加大国家创新型城市的配套辅助政策支持力度。鉴于政策的时效性机制，为使国家创新型城市经济发展质量得到更大程度的提升，在政策效果逐渐增加期限内，国家或地区政府逐步出台辅助政策，并加大政策支持力度，如人才引进和激励政策等，力图使政策效果最大化。

(3)加强地区高端生产性服务业集聚建设。鉴于高端生产性服务业在国民经济增长中的重要作用，国家创新型城市建设需要高端生产性服务业提供更多科技、资金和配套服务的支持，通过高端生产性服务业的专业化集聚及与制造业的协同集聚，在创新价值链中发挥正向溢出效应，使区域经济向高质量发展阶段过渡。