基于有限元强度折减法的单双面边坡稳定性分析*
高 冯 李小军 迟明杰
(①中国地震局地球物理研究所,北京 100081,中国) (②中国地震灾害防御中心,北京 100029,中国) (③北京工业大学建筑学院,北京 100124,中国)
0 引 言
岩土边坡失稳是常见的地质灾害,特别是大地震发生时,地震影响区往往会发生大量的河湖岸和山体滑坡,岩土边坡失稳及其影响问题成为工程建设所关注的重要岩土工程问题。极限平衡法和有限元强度折减法是目前工程实际中开展边坡稳定分析的最主要方法(吕庆等,2008;柳林超等,2009;张永明等,2009;陈力华等,2012)。相较于极限平衡法,有限元强度折减法具有较好的灵活性易于处理复杂的岩土边坡问题,通过引入土体弹-塑性本构关系直接计算出土体塑性应变区的出现和扩展,在边坡可能存在的滑动面位置不了解的情况下可计算确定坡体失稳的滑动面,包括其形状和位置。针对复杂的岩土边坡问题采用有限元模型进行计算分析,虽然计算量往往巨大,但随着非线性有限元分析方法的发展和高性能计算机的利用,岩土边坡稳定性分析的有限元法应用越来越普遍。
控制岩土边坡稳定性的土体力学参数主要有岩土介质的黏聚力、内摩擦角、弹性模量和泊松比,其中土体的黏聚力和内摩擦角相比弹性模量和泊松比是更为重要的影响参数(潘新恩,2014),进一步在土体出现塑性状态后,土体的黏聚力和内摩擦角会对土体边坡的稳定性起到控制性作用。以往针对单面边坡稳定性问题较多,研究手段和方法包括振动台试验分析(李果等,2016;关振长等,2017)、数值模拟分析(赵尚毅等,2002;Bouckovalas et al.,2005;李春忠等,2006;祁生文,2006;介玉新等,2017)等,一些研究成果被应用于实际边坡工程处理中。也有学者利用双面边坡模型开展了边坡稳定性研究,徐光兴等(2008)进行了双面土体边坡模型的振动台试验,试验展示了边坡动力特性及破坏状况。总体上看,对双面边坡稳定性的研究工作相对较少。然而,大地震现场调查工作中发现地震极震区存在不少双面边坡的滑坡现象,如2008年汶川MS8.0级地震(李小军等,2008;许强等,2010)。本文采用强度折减有限元法并借助于非线性有限元计算软件ABAQUS,计算分析土体边坡中的坡角、坡高、黏聚力和内摩擦角等参数对边坡稳定性影响,探讨单面和双面边坡的动力特性和稳定性之间的差异。
1 计算分析方法
1.1 有限元强度折减法
Zienkiewicz et al.(1975)提出了强度折减法,并以在外荷载保持不变的情况下,边坡内土体所发挥的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比定义了抗剪强度折减系数(栾茂田等,2003)。在某种意义上说这一抗剪强度折减系数(如果边坡内所有土体抗剪强度的发挥程度相同)相当于边坡整体稳定安全系数,也即强度储备安全系数,与Bishop(1954)在极限平衡法中所给的稳定安全系数在概念上具有一致性。
强度折减法中,首先选取一个初始折减系数Fi,而后进行土体强度参数折减计算得到新的强度参数ci和φi,但弹性模量E和泊松比ν假定不变。强度参数折减计算采用下式:
(1)
采用强度折减参数ci和φi开展有限元模型计算,并基于计算结果调整折减系数Fi,实现迭代计算分析,当土体边坡计算达到保持稳定的临界状态时结束迭代计算。由此得到边坡稳定安全系数FS,即迭代计算最后得到的折减系数。计算得到的FS越大,则表明所分析的边坡越稳定。
1.2 土体边坡失稳的判别
基于有限元强度折减法分析边坡稳定性,需要建立土体边坡是否达到极限状态而发生失稳破坏的计算判别准则。边坡失稳的判别准则决定着边坡整体稳定安全系数的计算结果合理性及影响到边坡失稳分析结论的可靠性。目前有限元模型计算研究和工程应用中较为普遍采用的土体边坡稳定临界状态的判别准则为(吕庆等,2008):(1)计算中出现不收敛;(2)坡面或顶部位移拐点出现;(3)连续塑性应变贯通区形成。
1.3 土体本构模型的选取
本文将土体考虑为完全弹-塑性体,假设屈服准则和破坏准则相同,且屈服准则采用Mohr-Coulomb准则。屈服准则的表达形式为(连镇营等,2001):
I1sinφ-3ccosφ=0
(2)
式中:c和φ为土体的黏聚力和内摩擦角;θ为应力罗德角;I1表示第一应力不变量;J2和J3表示第二和三应力偏张量。
在有限元模拟过程中,将单元高斯积分点上的应力处于破坏面之内的单元视为弹性状态;将位于破坏面上单元视为屈服状态;将处于破坏面之外的单元进行应力修正。塑性势函数采用式(3)所示的形式,以避免Mohr-Coulomb屈服面上的奇异线或尖角。
(3)
式中:ψ为剪胀角;其余同式(2)。
2 数值计算与结果分析
选择一个单面均质土体边坡模型(Dawson et al.,1999)作为参考计算模型,进行数值计算对比分析,以验证本文数值计算方法的可行性。计算土体边坡模型如图 1所示,边坡的几何尺寸为:坡高H=10im,坡角β=45°;边坡土体的物理力学参数为:黏聚力c=12.4ikPa,摩擦角φ=20°,容重γ=20ikN·m-3。基于极限平衡法可以得到,该计算模型的边坡稳定安全系数为1.0(费康等,2017)。
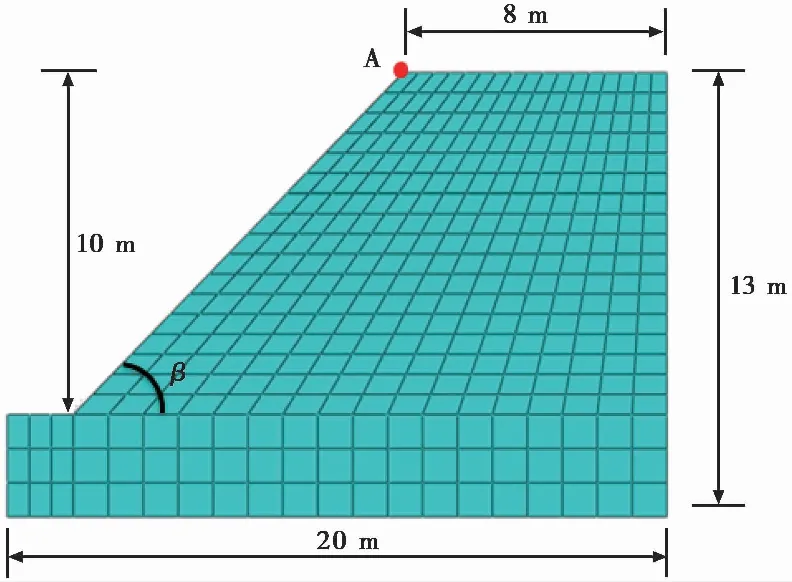
图 1 单面均质土体边坡模型Fig. 1 Single side homogeneous soil slope model
2.1 模拟方法及方法验证
采用ABAQUS计算软件结合强度折减法进行土体边坡模型的计算分析,计算中采用土体完全弹-塑性模型、Mohr-Coulomb准则和不考虑剪胀角影响的非关联流动法。首先针对参考计算模型,即图 1所示的单面均质土体边坡模型进行边坡稳定性计算。
计算得到模型顶部A点场变量FV1(强度折减系数)与水平位移U1的关系结果如图 2a,不同时刻下土体等效塑性分布如图 2b、图2c、图2d所示。图 2a显示FV1-U1曲线上存在一个拐点值,也就是边坡稳定状态的最小安全系数Fs值,从图 2b、图2c、图2d可以看到土体等效塑性应变区的分布、发展和贯通过程,在0.3241is时刻边坡土体塑性应变区出现贯通(图 2d),表明此时边坡发生失稳破坏。
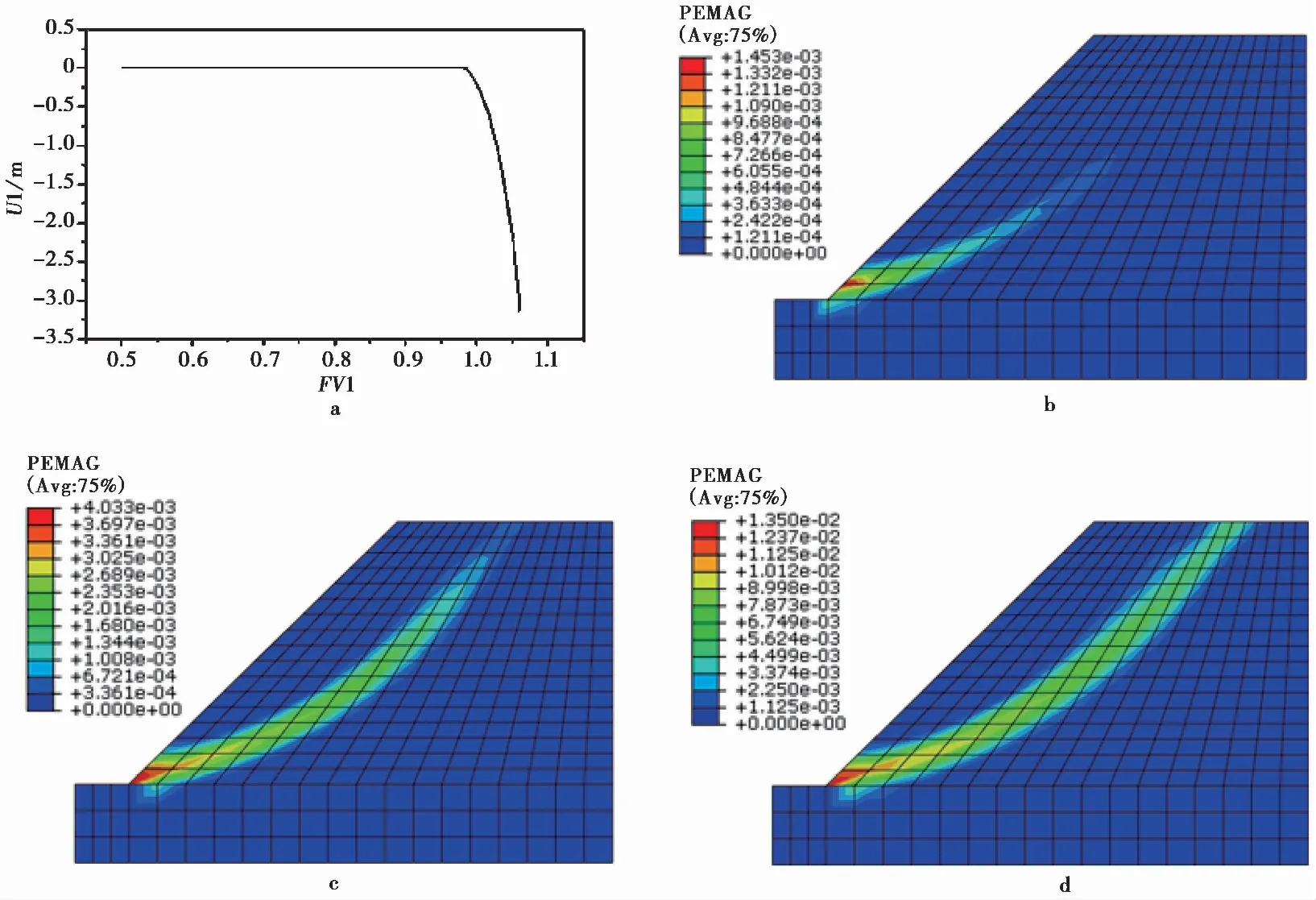
图 2 单面均质土体边坡稳定性分析计算结果Fig. 2 Computing results of the stability analysis of single side homogeneous soil slopea. A点FV1与U1的关系;b. t=0.3000 s时塑性区;c. t=0.3200 s时塑性区;d. t=0.3241 s时塑性区
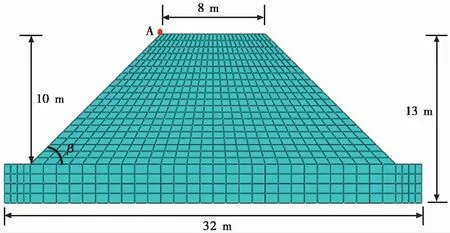
图 3 双面均质土体边坡模型Fig. 3 Double side homogeneous soil slope model
基于前面给出的土体边坡失稳的3种判别准则,计算得到了对应3个不同准则(计算中出现不收敛,坡面或顶部位移拐点出现,连续塑性应变贯通区形成)的边坡整体稳定安全系数Fs分别为1.06、0.99、0.99,系数值均接近1.0,与极限平衡法的结果基本一致。
为开展边坡类型影响研究,建立了一个双面均质土体边坡模型(图 3)。模型中,边坡的几何尺寸和土体的物理力学参数与上面分析的单面均质土体边坡模型的相同,即H=10im、β=45°、c=12.4ikPa、φ=20°、γ=20ikN·m-3,而坡顶宽度a取值8im。计算得到双面边坡的稳定安全系数,其计算结果如图 4所示。图 4显示了模型顶部A点场变量FV1与水平位移U1的关系结果和不同时刻t的土体等效塑性区的分布。
表 1给出了单面边坡模型和双面边坡模型计算得到的在3种判别准则下的安全系数计算结果,其中Fs1、Fs2、Fs3分别为有限元模型计算分析中基于计算中出现不收敛、坡面或顶部位移拐点出现、连续塑性应变贯通区形成的判别准则对应的计算安全系数。
表 1 单面和双面边坡稳定安全系数对比Table1 Comparison of the factors of safety of single side slope and double side slope

稳定安全系数Fs1Fs2Fs3单面边坡模型1.060.990.99双面边坡模型1.040.980.98
表 1中的数据表明,无论是采用哪一个判别准则,单面和双面土体边坡的安全系数均有一定的差异,计算中出现不收敛判别准则下的安全系数相对较大,而坡面或顶部位移拐点出现和连续塑性应变贯通区形成判别准则的安全系数计算值相同而且十分接近1.0;双面土体边坡的安全系数略小于单面土体边坡。综合考虑,本文后续工作中将以坡面顶部的位移拐点出现这一判别准则来进行土体边坡的稳定性分析。
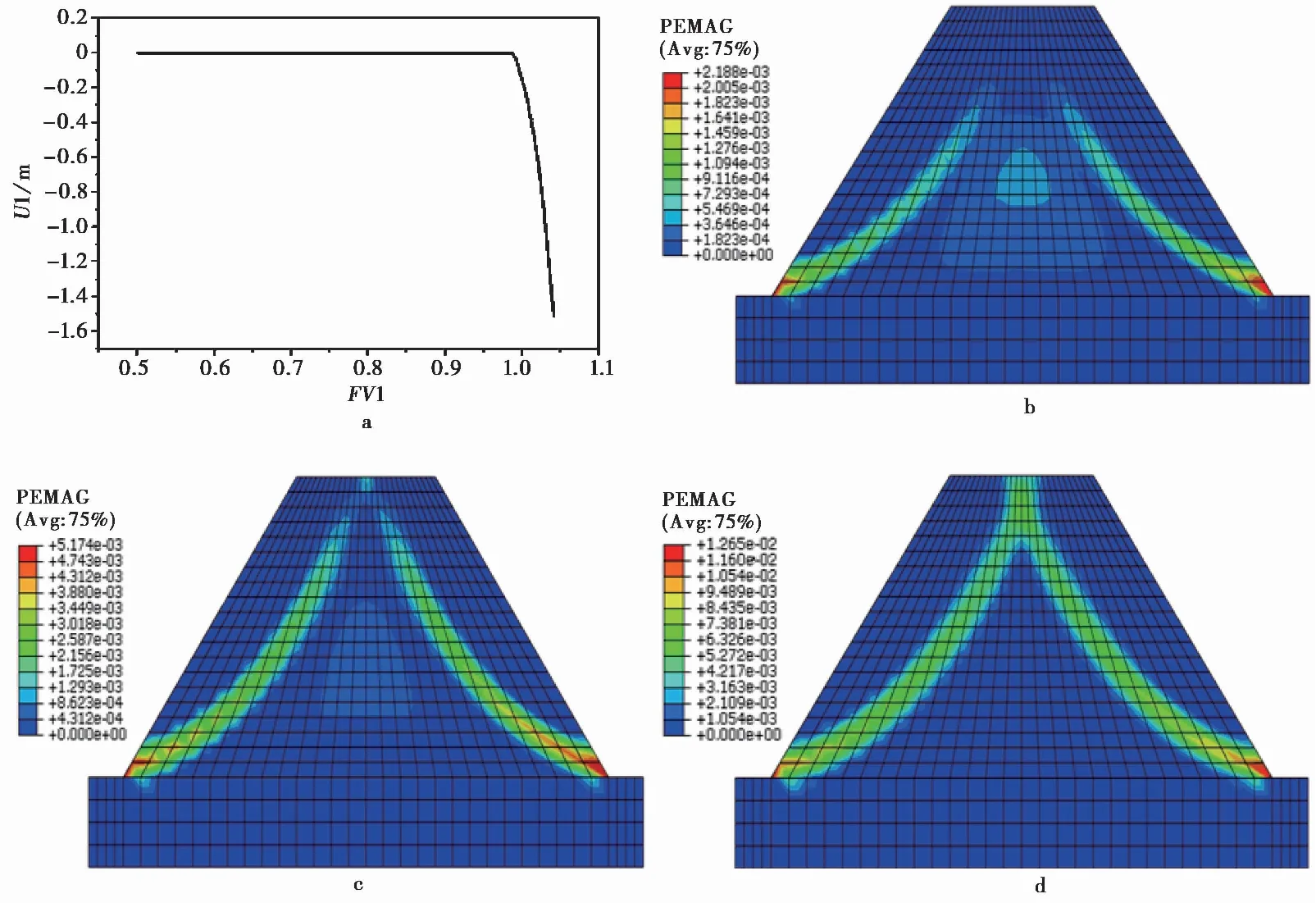
图 4 双单面均质土体边坡稳定性分析计算结果Fig. 4 Computing results of the stability analysis of double side homogeneous soil slopea. A点FV1与U1的关系;b. t=0.3000 s时塑性区;c. t=0.3200 s时塑性区;d. t=0.3249 s时塑性区
2.2 单面和双面边坡稳定性对参数的敏感性及对比
针对上文分析的单面和双面均质土体边坡模型,开展边坡稳定性对模型参数的敏感性分析,探讨边坡的几何尺寸和土体的物理力学参数变化对边坡稳定性影响的特点与规律。分别讨论边坡的4个参数坡角β、黏聚力c、摩擦角φ与坡高h对边坡稳定性的影响,但计算分析中仅分别单独考虑一个参数变化的影响,而固定其他参数值。
2.2.1 坡角的影响
分别将坡角β取值为35°、40°、45°、50°、55°和60°,其他参数固定取值即h=10im、γ=20ikN·m-3、c=12.4ikPa、φ=20°,进行模型计算分析。单面和双面均质土体边坡模型的计算结果对比如表 2与图 5所示。
表 2 不同坡角β取值对应的单面和双面边坡稳定安全系数Fs计算值Table2 Values of factors of safety Fs of single and double side slopes with different slope angles β
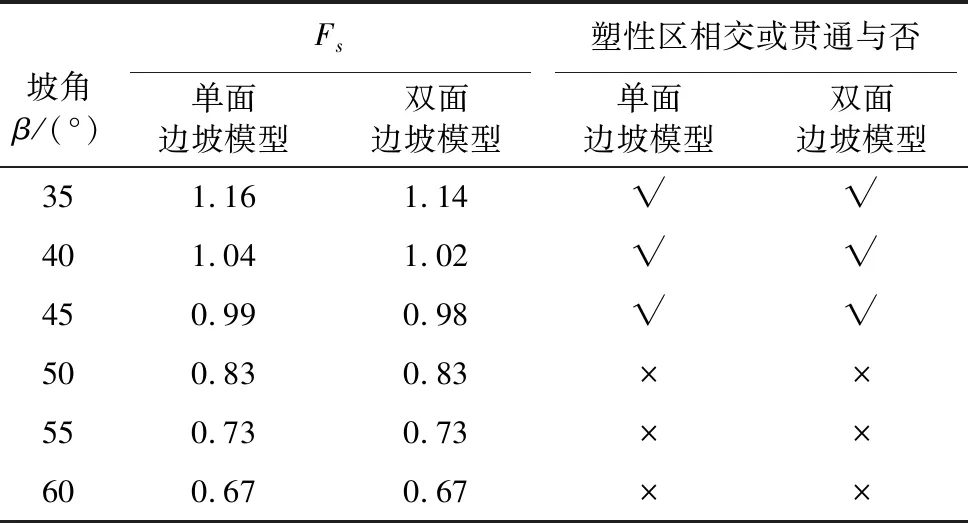
坡角β/(°)Fs塑性区相交或贯通与否 单面边坡模型双面边坡模型单面边坡模型双面边坡模型351.161.14√√401.041.02√√450.990.98√√500.830.83××550.730.73××600.670.67××
计算结果表明,无论是单面还是双面边坡模型其计算安全系数均显著受坡角影响,且随着坡角的增大近于线性减小。当β<50°时,两类边坡的稳定性有一定的差异,单面边坡稳定性略好一些;当β≥50°时,两类边坡的稳定性无差异。另外,看出基于坡面顶部的位移拐点出现的判别准则得到稳定性临界状态时,β<50°时边坡出现塑性区相交或贯通现象,而β≥50°时边坡并未出现塑性区相交或贯通现象。这说明此两种判别准则之间存在一定的差异。

图 5 边坡稳定安全系数Fs随坡角β的变化Fig. 5 Factors of safety Fs of side slopes with slope angle β

图 6 边坡稳定安全系数Fs随黏聚力c的变化Fig. 6 Variation of factor of safety Fs of slopes with cohesive strength c
2.2.2 黏聚力的影响
分别将黏聚力c取为4.4ikPa、6.4ikPa、8.4ikPa、12.4ikPa、16.4ikPa和20.4ikPa,其他参数固定取值即h=10im、β=45°、γ=20ikN·m-3、φ=20°,进行模型计算分析。单面和双面均质土体边坡模型的计算结果对比如表 3与图 6所示。
计算结果表明,无论是单面还是双面边坡模型其计算安全系数均显著受黏聚力影响,且随着黏聚力的增大近于线性增大。当c>8.4ikPa时,两类边坡的稳定性有一定的差异,单面边坡稳定性略好一些;当c≤8.4ikPa时,两类边坡的稳定性无差异。另外,看出基于坡面顶部的位移拐点出现的判别准则得到稳定性临界状态时,c>8.4ikPa时边坡出现塑性区相交或贯通现象,而c≤8.4ikPa时边坡并未出现塑性区相交或贯通现象。这说明此两种判别准则之间存在一定的差异。
表 3 不同黏聚力c对应的单面和双面边坡稳定安全系数Fs计算值Table3 Factor of safety Fs of single and double side slopes with different values of cohesive strength c
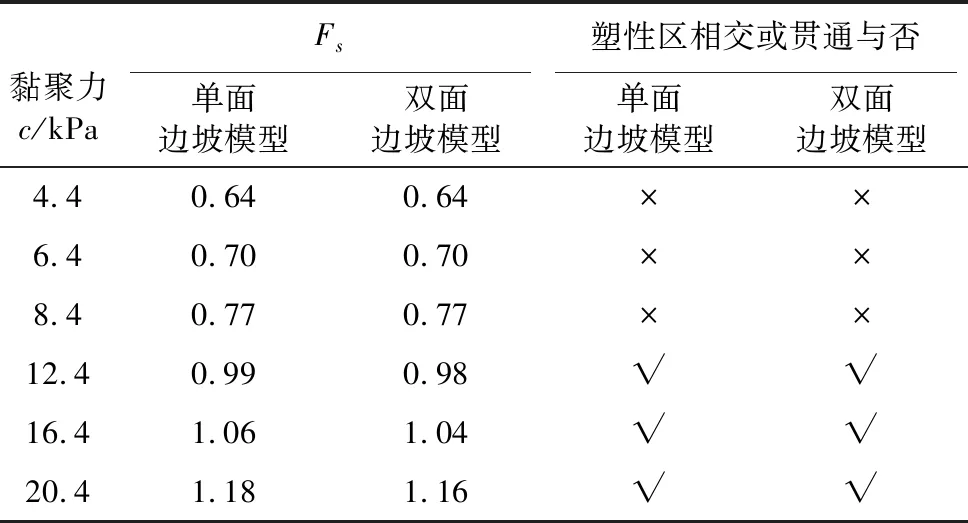
黏聚力c/kPaFs塑性区相交或贯通与否单面边坡模型双面边坡模型单面边坡模型双面边坡模型4.40.640.64××6.40.700.70××8.40.770.77××12.40.990.98√√16.41.061.04√√20.41.181.16√√
2.2.3 内摩擦角的影响
分别将内摩擦角φ取为10°、15°、20°、25°、30°和35°,其他参数固定取值即h=10im、β=45°、γ=20ikN·m-3、c=12.4ikPa,进行模型计算分析。单面和双面均质土体边坡模型的计算结果对比如表 4与图 7所示。
计算结果表明,无论是单面还是双面边坡模型其计算安全系数均显著受摩擦角影响,且随着摩擦角的增大近于线性增加。当φ<25°时,两类边坡的稳定性有一定的差异,单面边坡稳定性略好一些;当φ≥25°时,两类边坡的稳定性无差异。另外,看出基于坡面顶部的位移拐点出现的判别准则得到稳定性临界状态时,φ<25°时边坡出现塑性区相交或贯通现象,而φ≥25°时边坡并未出现塑性区相交或贯通现象。这说明此两种判别准则之间存在差异。
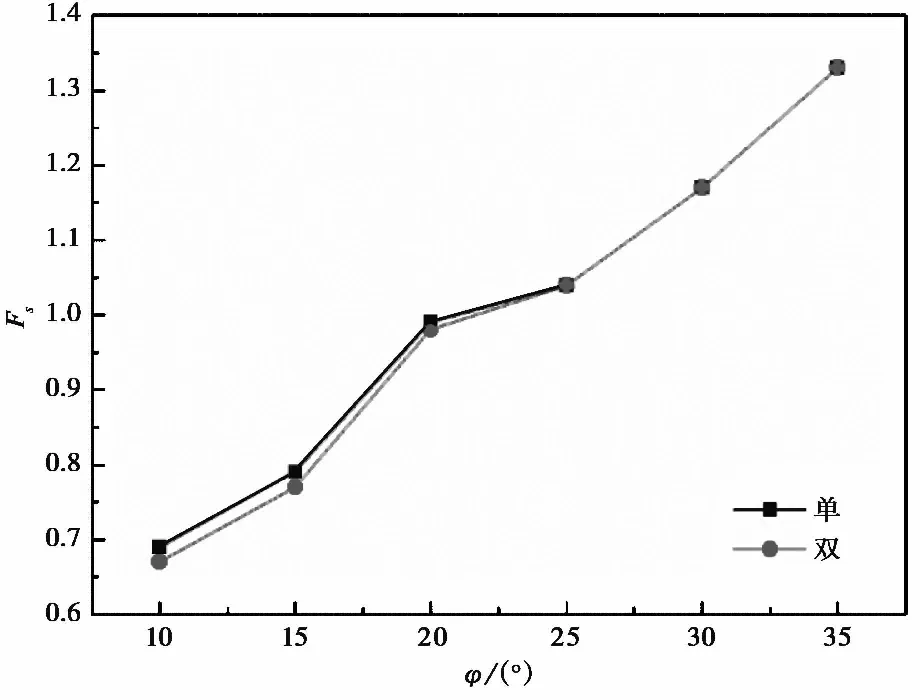
图 7 边坡稳定安全系数Fs随内摩擦角φ的变化Fig. 7 Variation of factors of safety Fs of slopes with friction angle φ
表 4 不同内摩擦角φ对应的单面和双面边坡稳定安全系数Fs计算值Table4 Factor of safety Fs of single and double side slopes with different values of friction angle φ

内摩擦角φ/(°)Fs塑性区相交或贯通与否单面边坡模型双面边坡模型单面边坡模型双面边坡模型100.690.67√√150.790.77√√200.990.98√√251.041.04××301.171.17××351.331.33××
表 5 不同坡高h对应的单面和双面边坡稳定安全系数Fs计算值Table5 Factors of safety Fs of single and double side slopes with different values of slope height h

坡高h/mFs塑性区相交或贯通与否 单面边坡模型双面边坡模型单面边坡模型双面边坡模型61.321.30√√81.111.10√√100.990.98√√120.860.85√√140.800.80××160.750.75××180.720.72××

图 8 边坡稳定安全系数Fs随坡高h的变化Fig. 8 Variation of factors of safety Fs of slopes with slope height h
2.2.4 坡高的影响
分别将坡高h的值取为6im、8im、10im、12im、14im、16im和18im,其他参数固定取值即β=45°、γ=20ikN·m-3、c=12.4ikPa、φ=20°,进行模型计算分析。单面和双面均质土体边坡模型的计算结果对比如表 5与图 8所示。
计算结果表明,无论是单面还是双面边坡模型其计算安全系数均显著受坡高影响,且随着坡高的增大呈双曲线形式减小,减小的趋势逐渐变缓。当h<14im时,两类边坡的稳定性有一定的差异,单面边坡稳定性略好一些;当h≥14im时,两类边坡的稳定性无差异。另外,看出基于坡面顶部的位移拐点出现的判别准则得到稳定性临界状态时,h<14im时边坡出现塑性区相交或贯通现象,而h≥14im时边坡并未出现塑性区相交或贯通现象。这说明此两种判别准则之间存在差异。
从上文中坡角、黏聚力、内摩擦角与坡高摩擦角与坡高等4个参数的单独变化对边坡稳定性影响的分析可进一步发现,4个参数对单面和双面边坡稳定性的影响及其差异性具有非常一致的特征:总体上无论这4个参数如何变化,单面边坡稳定性略好于双面边坡稳定性,但当坡角、内摩擦角或坡高大于某一值(如β≥50°、φ≥25°或h≥14im),或黏聚力小于某一值(如c≤8.4ikPa)时,单面和双面边坡稳定性计算结果呈现一致性,此时可以把双面边坡简化为单面边坡进行分析。进一步分析边坡的塑性应变区的分布、发展和贯通过程,发现单面和双面边坡稳定性出现差异的原因是,对于一些边坡参数取值情况,由于双面边坡两侧出现的塑性应变区会发生先相交后贯通出坡顶的现象,而且在双面边坡两侧塑性应变区相交时,坡顶位移会出现突变,从而降低双面边坡稳定性。
3 结 论
利用强度折减有限元分析方法,采用非线性有限元分析软件ABAQUS进行边坡模型计算,探讨了典型单面和双面土体边坡的稳定性。分析了土体边坡几何参数和物理参数,包括坡角、坡高、黏聚力和内摩擦角,对单面和双面土体边坡稳定性影响的特征及差异性,数值模拟展现了土体边坡塑性应变区的分布、发展和贯通过程。得到的主要研究结果和认识如下:
(1)坡角、坡高、黏聚力和内摩擦角等边坡几何参数和物理参数对单面与双面土体边坡稳定性的影响规律基本一致;随着坡角的增加或黏聚力和内摩擦角的减小边坡安全性系数值近似线性减小,随着坡高的增大边坡安全性系数值呈双曲线形式减小且减小趋势逐渐变缓。
(2)单面与双面土体边坡稳定性有一定的差异,单面边坡稳定性略好于双面边坡稳定性稳。只有当坡角、内摩擦角或坡高大于某一值,或黏聚力小于某一值时,单面与双面边坡稳定性趋于一致。建议实际工程中边坡稳定性评价考虑采用双面边坡甚至更复杂边坡分析模型。
(3)基于坡面顶部的位移拐点出现的判别准则得到稳定性临界状态时,边坡并不一定出现塑性应变区贯通现象,说明坡面顶部的位移拐点出现和连续塑性应变贯通区形成这两种判别准则之间存在差异。建议利用基于多种稳定性判别准则的计算结果综合分析。
需要指出的是,本文的结论是基于典型均质土体边坡模型,也没有考虑多种参数组合情况的影响,研究成果的普适性如何有待进一步工作,特别是要进一步关注对称性与非对称双面边坡的稳定性差异。

