纵波波速与混凝土坍落度及贯入阻力之间相关性试验研究

龙士国，余 高，刘 佩，李 婷

(湘潭大学土木工程与力学学院，湖南湘潭411105)

0 引 言

预拌混凝土在工程中的应用越来越广泛，其是由水泥、骨料、水，外加剂及掺合料按照一定比例混合的混凝土拌合物，在集中搅拌站经搅拌出售并采用运输车在规定时间运至使用地点[1]。与现场搅拌混凝土相比，预拌混凝土虽然节省了资源，减少了施工现场废料的产生，但由于搅拌站和施工现场的距离，混凝土在运输过程中，会造成坍落度的损失，尤其是在掺入外加剂和在高温天气的情况下，坍落度损失更为严重。实际工程中往往由于对坍落度损失考虑不周，在现场浇筑时，导致泵送或密实成型困难，从而影响施工效率和混凝土质量，而目前对于混凝土坍落度的控制采用的是坍落度法。凝结时间是混凝土拌合物的一项重要指标，它对混凝土的搅拌、运输、施工以及早龄期混凝土结构开裂控制与风险评估具有重要的参考和指导作用[2]。初凝、终凝时间的确定采用贯入阻力法，并规定贯入阻力为3.5 MPa和28 Mpa，对应于混凝土的初、终凝时间。无论是坍落度法和贯入阻力法都受人为因素的影响，操作不便且未能很好地反映混凝土的特征。

超声波波速法是过去几十年来发展的一种混凝土早期水化过程监测方法。通过监测超声波速度随时间的变化，可以确定早期的物理化学反应和随后的微观结构发展[3]。国内外学者在利用超声波监测混凝土早期凝结硬化方面做了一系列工作。苏安双[4]利用NM-4A非金属超声检测分析仪监测了不同水灰比、不同矿物掺料等高性能混凝土的波速随时间的变化关系，并将波速由快速增长转为缓慢增长的时刻定义为浆体终凝时间。杨晓星[5]利用超声波对早龄期混凝土凝结硬化过程进行了监测，获得了超声波声学参数与龄期之间的关系，将声学参数与初终凝时间联系起来。Lu等[6]进行了实验测试，以研究混凝土搅拌成型后最初1 000 min内超声波速度的演变，与Kong等[7]类似，他们将超声波速度的变化分为三个阶段，即：阶段I，缓慢增加(休眠)阶段；阶段II，快速增加阶段；阶段III，稳定阶段。但这些研究涉及的基本上都是混凝土的整个凝结硬化的过程，没有在声波波速与早期混凝土经时坍落度之间建立起联系。超声波分为横波(S 波)和纵波(P 波)，在早期时候混凝土被认为是粘滞的悬浮体，这种情况下只有纵波可以传播，而横波无法传播，因此在监测混凝土凝结硬化过程时，采用的是纵波。本文配置了不同水灰比的混凝土，研究了混凝土自搅拌振捣成型后12 h内纵波波速的变化，与坍落度、坍落度损失率、贯入阻力建立起联系，并分析了它们之间的关系。对今后预拌混凝土坍落度控制以及初凝、终凝时间的确定具有一定的参考价值。

1 试验方案

1.1 试验原材料

(1) 水泥。根据试验的需要，选用湖南湘乡棋梓桥水泥有限公司生产P·O42.5(旋窑)生产的硅酸盐水泥。

(2) 细骨料。砂子的选取应该满足GB/T 14684-2011《建筑用砂》[8]的要求。

(3) 粗骨料。颗粒级配为5～20 mm连续级配，粒型为不规则的多边形。其各项指标符合GB/T 14685-2011《建设用卵石、碎石》[9]的要求。

(4) 水。实验所用的水为湘潭地区来自于湘江的自来水。

1.2 试样配比与制备

试验中采用的材料每立方米中的用量如表1所示，改变用水量以获得不同的配合比。

配置的原材料采用二次投料法(预拌水泥砂浆法)搅拌，先将准备好的水、水泥、砂子投入搅拌机，充分搅拌至水泥砂浆均匀后，再投入石子搅拌得到均匀的混凝土。将搅拌均匀的混凝土放入试模中，将试模放在混凝土振动台上，开启振动台，设置振动时间为60 s。振动的目的是减少混凝土内部的空隙，使得混凝土各成分之间更加密实。

表1 不同水灰配合比的混凝土Table1 Concrete mixture with different water-cement ratios

1.3 测试原理和装置

装混凝土的试模由亚克力板制成，内部尺寸为100 mm×100 mm×300 mm，壁厚为5 mm。为减小壁对声波传播的影响，在试模中心两侧处挖一个直径为35 mm，厚度为5 mm的圆孔，用透明胶布封住圆孔，在胶布上涂上黄油进行耦合，使得换能器与混凝土拌合物接触良好，然后固定试验装置。试验装置如图1所示，利用多功能声波测试仪对声波信号进行采集和分析。当对硬化混凝土结构进行健康监测时，因为硬化混凝土的声衰减系数较低，采用频率20 kHz以上的超声波效果非常好。然而，对于新拌的混凝土，声波在传播过程中衰减系数非常大，信号随着测试频率的增加而降低[8]。尤其在前几个小时内，声波的衰减更大，故本文中采用频率为5 kHz的换能器。从水泥加水搅拌至测得第一个波形，其间大概经历了30 min，以此时时间作为0时，从采集到的第一个波形开始将数据采集频率设置成每30 min一次。

图1 试验装置图Fig.1 Test device diagram

2 试验结果与分析

2.1 纵波波速变化规律

不同龄期混凝土纵波波速如图2所示。其中波速v的计算是由波传播的距离L以及接收到第一个波形的时间t确定，在这里取L=10 cm，波速计算公式为v=L/t。由图2可知，刚拌制的混凝土其纵波波速很低，甚至低于在空气中的传播速度340 m·s-1。这主要有两方面的原因：(1) 根据Rapoport等[9]的观点，由于新拌混凝土中存在悬浮水泥颗粒，使得波的传播路径变长；(2) 根据Keating等[10]和Sayers等[11]的观点，这种现象是由于拌合水中有一定量的气泡，或者水泥颗粒中存在的大量微小气孔而夹杂着气泡，空气阻碍了波的传播，使波的传播路线复杂化。根据Harker等[12]的理论模型，可以证明空气含量对新拌混凝土纵波波速的影响。空气泡的存在严重影响纵波波速，混凝土拌合物中 1% 的含气量可以将波速从1 500 m·s-1降低至200 m·s-1左右。另一方面，骨料、水泥浆体之间与水分离，很少聚集在一起，水泥浆体与骨料之间处于分离状态，声波穿过水泥浆体与骨料之间时，由于两者声阻抗的不同，会不断地发生反射、折射，这也是造成波速比较低的另一个原因。

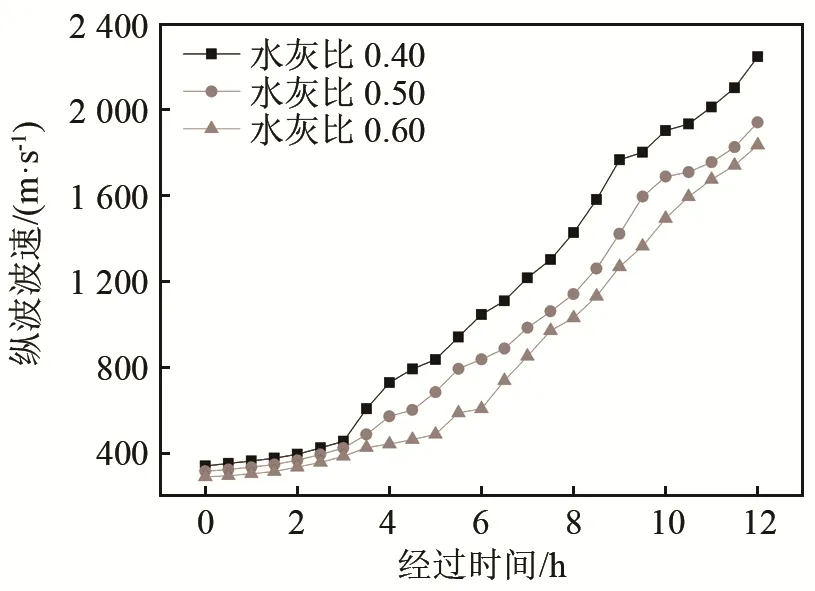
图2 不同水灰比混凝土拌合物纵波波速变化图Fig.2 Variations of the longitudinal wave velocity of concrete mixture with different water-cement ratios

在前3 h内，水灰比为0.40、0.50、0.60时，其纵波波速增长分别为33.3%、34.1%和32.9%，纵波波速变化较小，主要是因为此阶段处于水泥水化反应的潜伏期，此时水化反应程度较低，大部分水泥颗粒仍旧处于悬浮状态，未能与骨料之间形成连通结构。而随着时间的进行，水灰比为0.40、0.50和0.60的混凝土纵波波速的增长呈现了同样的规律，纵波波速都逐渐增大，这是由于水泥的快速固化，材料从悬浮液的状态变为多孔弹性固体的状态，混凝土逐渐固化，声波的传递路径由液相转变成固相。水泥产物的体积显著增加，这不仅使得大块糊状物致密化，而且使得界面过渡区致密化，并在水泥浆体和骨料之间形成良好的连接。在同一时刻，随着水灰比的增大，纵波波速逐渐减小，这主要有两方面原因。一方面是因为水泥加水拌合后，水灰比大的其固相颗粒的含量比水灰比小的要少。另一方面是因为水灰比的增加，使得水泥的用量更少，水泥浆体与骨料之间的连接更加疏松，孔隙更大。

2.2 混凝土经时坍落度与经时坍落度损失率

坍落度是指混凝土的和易性，具体来说是保证施工的正常进行，其中包括混凝土的保水性、流动性以及粘聚性，坍落度的测试主要采用坍落度法。测试方法如下：用一个上口100 mm、下口200 mm、高300 mm喇叭状坍落度筒，分3次装入混凝土，每次填装后用捣锤沿筒壁均匀由外向内击25下，捣实后抹平。由于混凝土自重产生坍落现象，用筒高减去坍落后混凝土的最高点高度，即为坍落度。随着时间的延迟，混凝土拌合物中的水泥水化，坍落度值将逐渐减小，这个过程称为坍落度损失，坍落度的损失值与初始坍落度的比值称为坍落度经时损失率。

图3为不同水灰比的混凝土坍落度经时损失曲线。由图3可知，水灰比为0.40、0.50和0.60的混凝土经过3 h后，坍落度损失分别为34 mm、43 mm和49 mm。其坍落度损失与起始坍落度有关，起始值越大，其损失量也越大。随着时间的延长，混凝土逐渐凝结硬化，坍落度不断减少。主要有以下几方面原因：(1) 因为水泥的水化反应，吸收和蒸发消耗了较多的拌合用水。(2) 因为粗细骨料的吸水作用使得拌合水减少。(3) 因为水泥水化产生的氢氧化钙、水化硅酸钙等水化产物，这些产物为针状晶体，较难运动，使新拌混凝土的黏度增大[13]。坍落度的大小与水灰比有关，同一时刻，水灰比越大，坍落度越大，这主要是因为当水泥量一定时，用水量越大时，骨料可以被水覆盖，使得砂石之间有较好的润滑。同时水泥浆体越稠，水泥浆体与骨料之间的摩擦力越小。

图4为不同水灰比的混凝土坍落度经时损失率曲线。

不同水灰比混凝土的坍落度损失率随时间的延长而增加，时间越长，坍落度损失率就越大，并且在同一时间，水灰比越小，混凝土坍落度损失率就越大。从图4中可以看出：水灰比为0.40的混凝土3 h后坍落度经时损失率达到了68%，大于水灰比为0.50时的61.43%和水灰比为0.60时的57.65%。

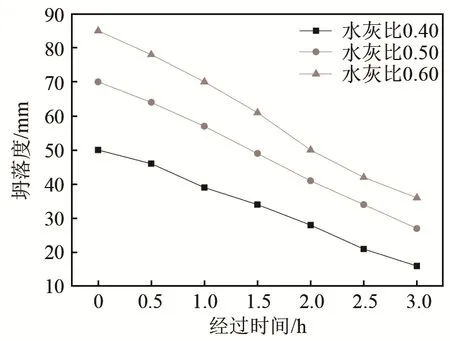
图3 不同水灰比经时坍落度曲线Fig.3 Variations of the concrete slump degree with time for different water-cement ratios

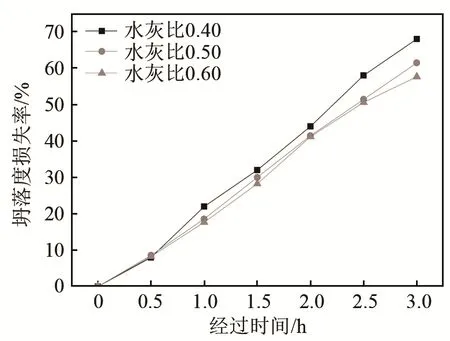
图4 不同水灰比坍落度经时损失率曲线Fig.4 Variations of the concrete slump loss rate with time for different water-cement ratios

2.3 混凝土拌合物初终凝时间的确定

通常情况下，可以用贯入阻力法来确定初凝、终凝时间。用孔径为5 mm的筛从塑性混凝土拌合物中筛取出砂浆，并拌合均匀，将温度控制在(20±3)℃。2 h后开始进行贯入度试验，测试前将筒底侧垫高约50 mm，使筒倾斜一定角度以吸去表面泌水。测试时将筒置于测试平台上读取砂浆与筒的合重作为基数，然后将测针与砂浆表面接触，按动贯入阻力仪的手柄，缓慢加压约10 s，使得测针贯入砂浆深度为25 mm时读取表盘压力值，此值减去砂浆与筒的合重后即为贯入压力(F)。从测得第一个贯入阻力值后，以后每隔30 min测一次贯入阻力值，如此反复直至贯入阻力大于28 MPa为止。

贯入阻力值的计算公式为

式中：P为贯入阻力(MPa)；F为贯入深度达25 mm时的压力；S为贯入测针截面积(mm2)。

以贯入阻力为纵坐标，时间为横坐标，绘制贯入阻力与时间关系曲线，以3.5 MPa及28 MPa画两条平行横坐标的直线，直线与曲线交点横坐标即为初凝与终凝时间。不同水灰比时贯入阻力与时间关系图如图5所示。

从图5可知，在早期的5 h内，3种不同水灰比混凝土的贯入阻力曲线靠得很近，说明在时间一定时，所对应的贯入阻力值很接近。而后虽然3种不同水灰比混凝土的贯入阻力曲线靠得较远，但其值相差并不大，即水灰比相差不大的情况下，初凝和终凝时间都比较接近。随着水灰比的增加，同一时刻的贯入阻力值减小，混凝土的凝结时间呈现出增长的趋势。从图5中可以看出，混凝土的凝结时间随着水灰比的增大，凝结时间有所延长。当水灰比从0.40增至0.60时，初凝时间从4.51 h延长到6.23 h，延长了38.14%；终凝时间从7.96 h延长到9.12 h，延长了14.57%。这主要是因为随着水灰比提高，单位混凝土拌合物中用水量增加，水泥颗粒相对浓度下降，水泥熟料水化反应产物需较长时间在浆体中累计达到一定浓度，从而导致混凝土凝结时间延迟[14]。

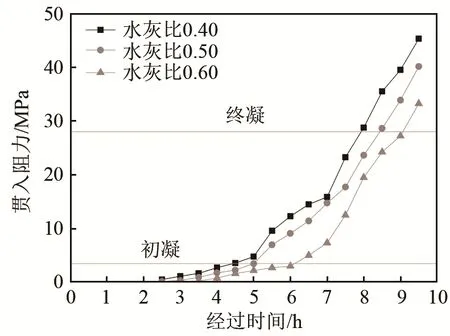
图5 不同水灰比时贯入阻力与时间关系图Fig.5 The relationship between concrete penetration resistance and time for different water-cement ratios

2.4 混凝土纵波波速与经时坍落度之间关系

为了更好说明纵波波速与坍落度之间的关系，对水灰比为0.40、0.50和0.60时的纵波波速与坍落度之间关系选择合适的曲线进行拟合，采用二次函数进行拟合：

式中：a、b、c为待定的回归系数，LS为坍落度。其拟合结果分别如图6～8所示，可以看出，随着时间的增长，坍落度损失率与波速之间具有负相关关系，且相关系数R2达到了0.980以上。

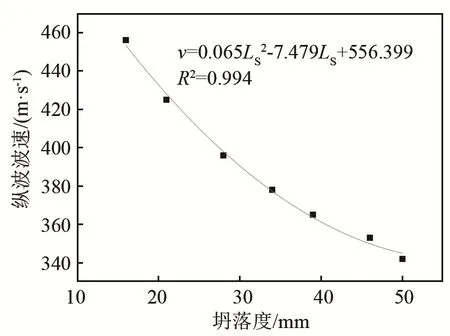
图6 水灰比为0.40时的纵波波速与坍落度关系图Fig.6 The relationship between longitudinal wave velocity and slump degree of the concrete with water-cement ratio of 0.40

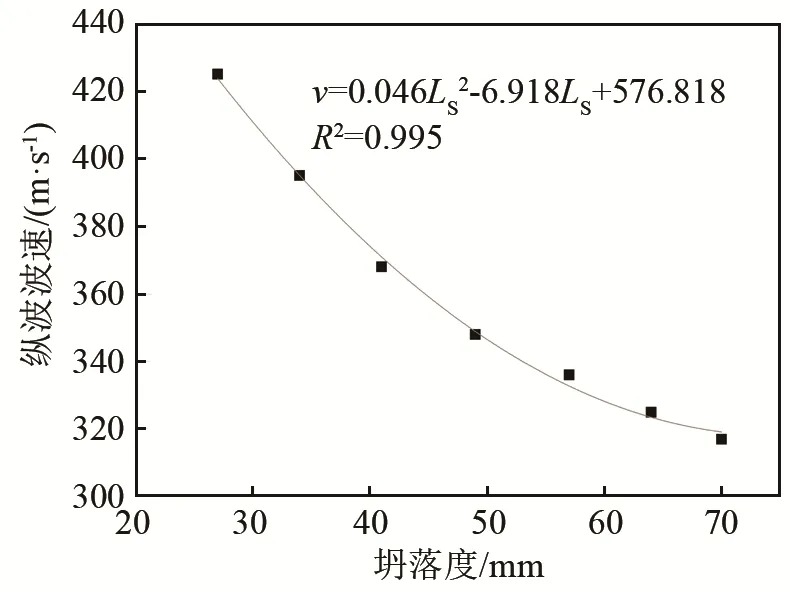
图7 水灰比为0.50时的纵波波速与坍落度关系图Fig.7 The relationship between longitudinal wave velocity and slump degree of the concrete with water-cement ratio of 0.50

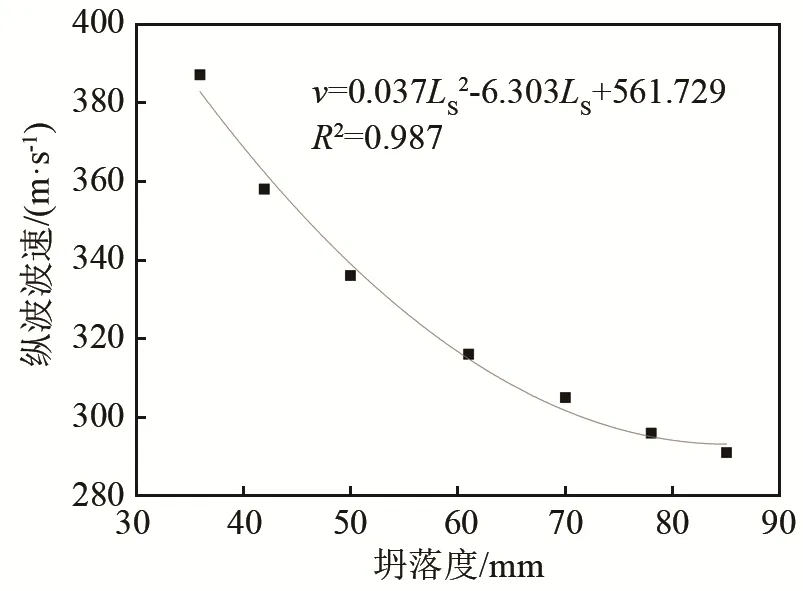
图8 水灰比为0.60时的纵波波速与坍落度关系图Fig.8 The relationship between longitudinal wave velocity and slump degree of the concrete with water-cement ratio of 0.60

对于水灰比为0.40时的混凝土拌合物，拟合结果为

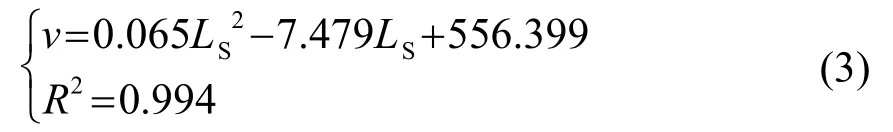
对于水灰比为0.50时的混凝土拌合物，拟合结果为

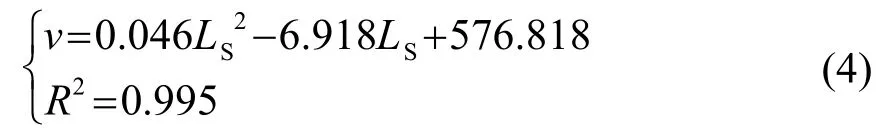
对于水灰比为0.60时的混凝土拌合物，拟合结果为

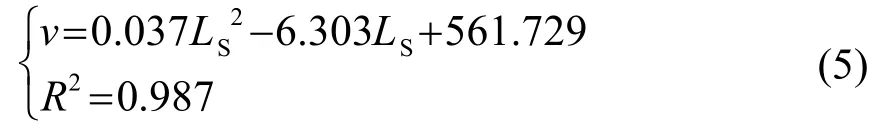
2.5 纵波波速与混凝土经时坍落度损失率之间关系

为了更好地说明纵波波速与混凝土经时坍落度损失率之间的关系，对水灰比为0.40、0.50和0.60的纵波波速与坍落度之间关系选择合适的曲线进行拟合，主要采用二次函数进行拟合：

式中：d、e、f为待定的回归系数。其拟合结果分别如图9～11所示，从图中可以看出，波速与坍落度损失率之间具有正相关关系，且相关系数R2达到了0.980以上。

对于水灰比为0.40的混凝土拌合物，拟合结果为

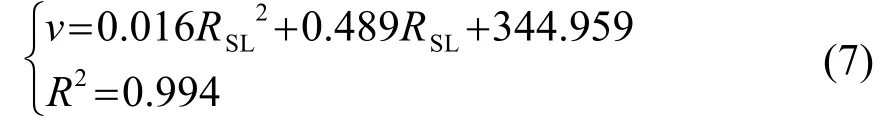
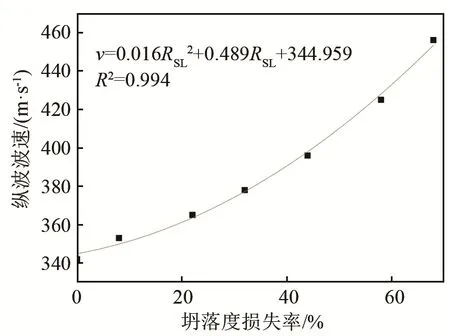
图9 水灰比为0.40时的纵波波速与坍落度损失率关系图Fig.9 The relationship between longitudinal wave velocity and slump loss rate of the concrete with water-cement ratio of 0.40

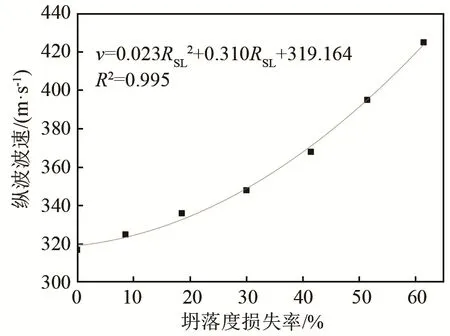
图10 水灰比为0.50时的纵波波速与坍落度损失率关系图Fig.10 The relationship between longitudinal wave velocity and slump loss rate of the concrete with water-cement ratio of 0.50

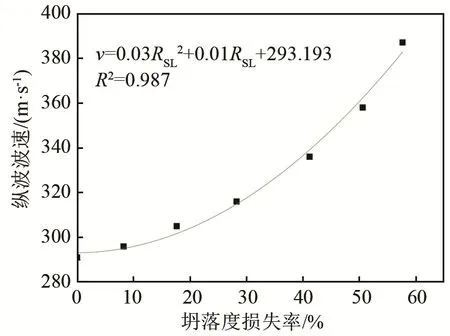
图11 水灰比为0.60时的纵波波速与坍落度损失率关系图Fig.11 The relationship between longitudinal wave velocity and slump loss rate of the concrete with water-cement ratio of 0.60

对于水灰比为0.50的混凝土拌合物，其拟合结果为

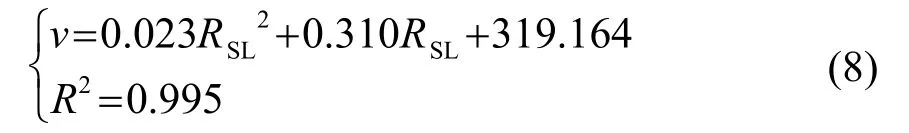
对于水灰比为0.60的混凝土拌合物，拟合结果为

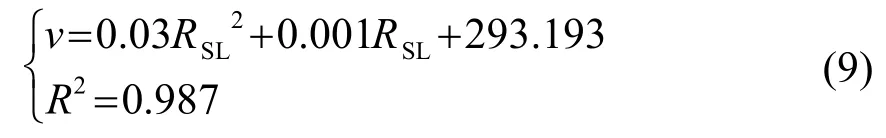
2.6 纵波波速与贯入阻力关系

混凝土拌合物不同时间波速与贯入阻力之间并没有统一的理论关系，本文依据混凝土不同时间波速与贯入阻力关系曲线，采用幂函数模型进行拟合，即：

其中：v为纵波波速；P为贯入阻力；a、b分别为回归系数。

图12分别为不同水灰比波速与贯入阻力间的关系曲线，从图12～14中可以看出，贯入阻力越大，纵波波速越大，呈现出幂指数增加的趋势，相关系数R2均在0.950以上。

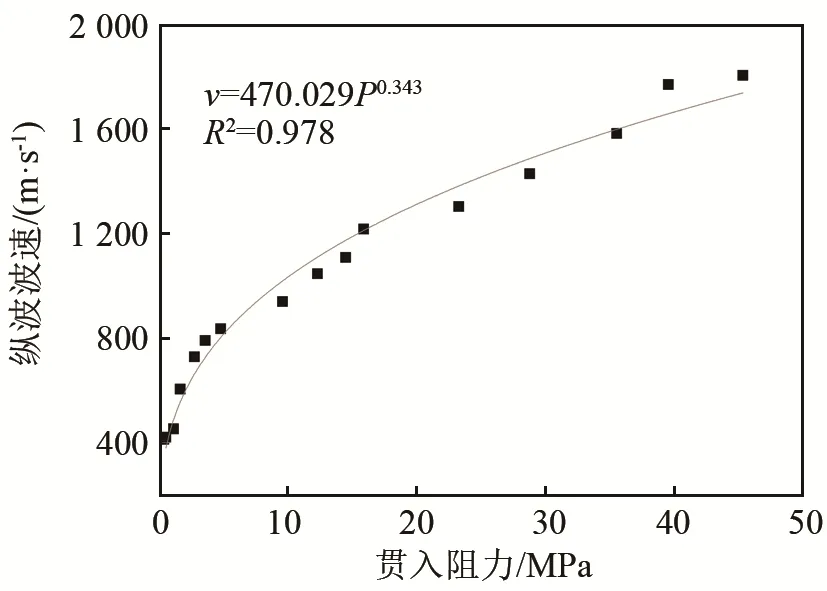
图12 水灰比为0.40时的纵波波速与贯入阻力关系图Fig.12 The relationship between longitudinal wave velocity and penetration resistance of the concrete with water-cement ratio of 0.40

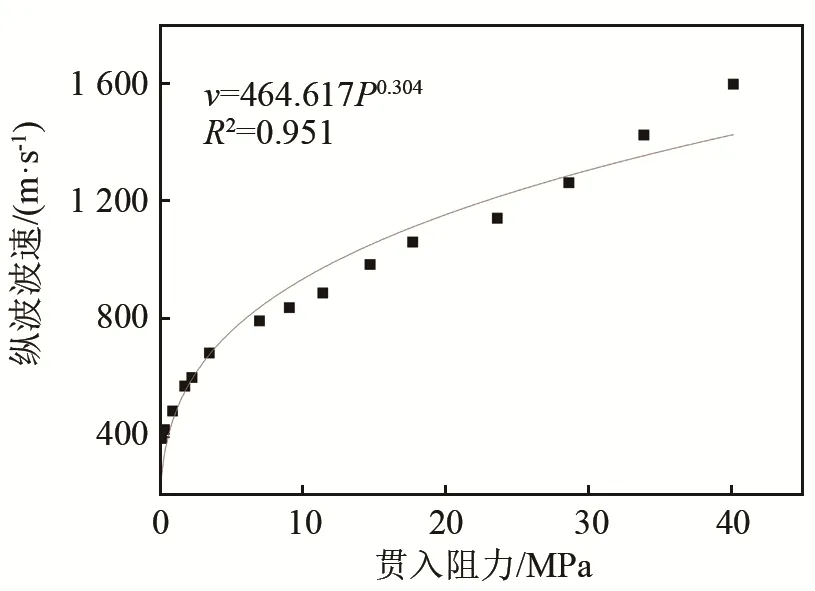
图13 水灰比为0.50时的波速与贯入阻力关系图Fig.13 The relationship between longitudinal wave velocity and penetration resistance of the concrete with water-cement ratio of 0.50

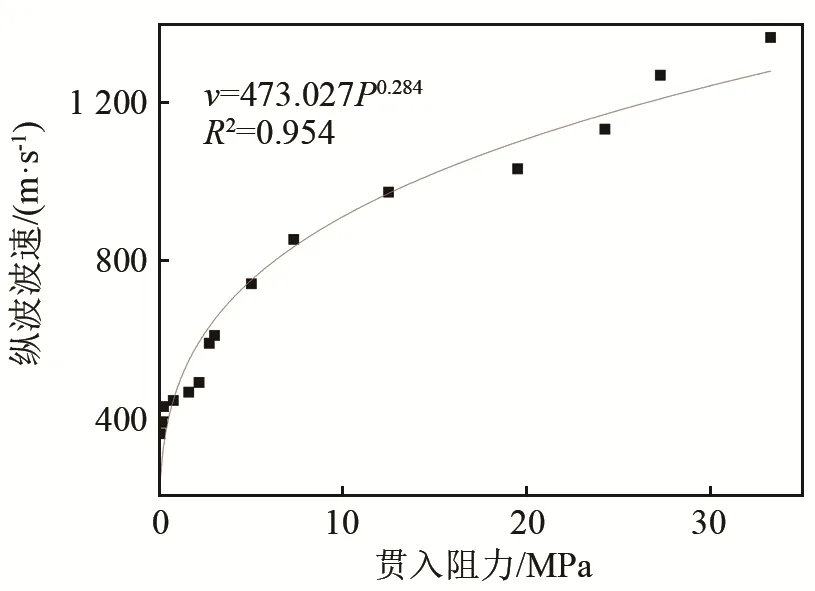
图14 水灰比为0.60时的波速与贯入阻力关系图Fig.14 The relationship between longitudinal wave velocity and penetration resistance of the concrete with water-cement ratio of 0.60

3 结 论

(1) 混凝土固化时，纵波波速随时间增长而不断变大，并且在同一时间，水灰比越小波速越大。前3 h内，纵波波速变化基本上很小，水灰比分别为0.40、0.50和0.60时，波速增长分别为33.3%、34.1%、32.9%；

(2) 随着时间的增长，不同水灰比的混凝土坍落度都明显呈减小的趋势，并且时间越长，坍落损失率越大。在前3 h，混凝土坍落度的损失率甚至可以达到60%以上；

(3) 贯入阻力法测得的初凝、终凝时间随着水灰比的增大而增大，当水灰比从0.40增至0.60时，初凝时间从4.51 h延长到6.23 h，延长了38.14%；终凝时间从7.96 h延长到9.12 h，延长了14.57%。

(4) 纵波波速与混凝土坍落度之间具有正相关关系，而纵波波速与混凝土坍落度损失率之间却是负相关关系。采用二次函数拟合更能反映纵波波速与坍落度以及与坍落度损失率之间的关系。

(5) 通过建立混凝土不同时间纵波波速与贯入阻力的关系，并采用幂函数模型进行拟合，发现波速与贯入阻力间拟合效果良好。