基于均匀同心圆阵列的近场宽带波束形成
孟子健,王沛曌,陈海华,2
1.南开大学 电子信息与光学工程学院,天津 300350;2.天津市光电传感器与传感网络技术重点实验室,天津 300350)
0 引言
自适应波束形成技术通过改变波束形成权重系数来抑制干扰信号并提高期望信号的接收增益。近年来,随着移动通信的发展和数字信号处理技术的广泛应用,自适应波束形成技术除了在雷达、声纳、空间滤波和定位等领域发挥重要作用外,同时也在麦克风阵列语音处理、无线通信等方向有了长足发展[1]。
传统波束形成法一般假设信号源与阵列中心的距离远大于阵列尺寸,即满足信号处于阵列远场的假设,因而可用平面波来近似到达信号[2]。在雷达和无线通信等应用系统中,上述假设较合理,其近似误差较小。然而,在许多其他场合中,如麦克风阵列语音处理、医学成像等领域,信号源与阵列的距离通常较短。在这种情况下,把到达阵列的信号近似为平面波所带来的误差较大,这将使波束形成的性能急剧降低。因此,国内外学者提出了多种近场波束形成方法,如用时延来弥补传感器之间的信号延迟差异,或通过近似曲率来弥补近场误差。文献[3]提出了一种可使波束聚焦于任意径向距离的方法,极大地扩展了传统波束形成方法的应用范围。
此外,设计宽带信号的波束形成还存在一个问题,即阵列响应会随着频率的变化而变化。在近场宽带阵列中,情形更复杂。在某些情况下,阵列响应在信号的高频段呈现远场信号的特点,而在信号的低频段则呈现近场信号的特点[4]。传统宽带阵列信号处理采用带自适应系数的抽头延迟线(TDL)滤波器,TDL抽头个数与信号带宽成正比,因而其计算复杂度和硬件复杂度随着带宽的增加而急剧升高[5]。相较于TDL法,子带分解技术、部分自适应波束形成法和频率响应不变波束形成器(FIB)[6]等方法的计算复杂度均有降低。传统的FIB法以均匀线性阵列为基础,由于均匀圆阵(UCA)的空间对称性,基于其设计的FIB具有电子可旋转特性,即波束形成的聚焦方向可通过改变阵列权重来旋转。此外,基于其对称特性,UCA-FIB的频率补偿网络与波束形成权重可以分开设计,故可预先离线设计以补偿网络,仅剩波束形成权重系数由自适应算法在线设计。因此,与其他宽带Beamforming算法相比,UCA-FIB在线运算复杂度较低[7]。在此基础上改进得到的均匀同心圆阵列(UCCA)FIB可缓解UCA-FIB中带宽受限的问题[8]。
本文提出了一种新的频率不变近场宽带波束形成的方法。该方法采用UCCA,借助多个阵列圆环间的相互补偿作用,可在更宽的频带上实现频率响应不变的近场宽带波束形成。该方法首先将同一个阵列环上各天线接收到的信号转化为相位模式,再将多个阵列环上对应的相位模式信号叠加。每路叠加后的相位模式信号通过近场矫正因子和频率补偿网络进行补偿,以消除近场效应和宽带信号的频率依赖性,最后使用波束形成权向量系数对所有相位模式信号进行加权求和,得到阵列的输出信号。鉴于UCCA的对称性,近场修正系数和频率补偿网络与波束形成权重向量可分开设计,因而前两者可预先离线完成,而波束形成系数可根据信号到达角进行自适应调整,极大地降低了系统的计算复杂度。仿真结果表明,该方法能够获得理想的具有频率不变特性的波束图。与其他自适应波束形成法相比,UCCA-FIB可大幅提高波束形成的性能。
1 近场UCCA-FIB原理

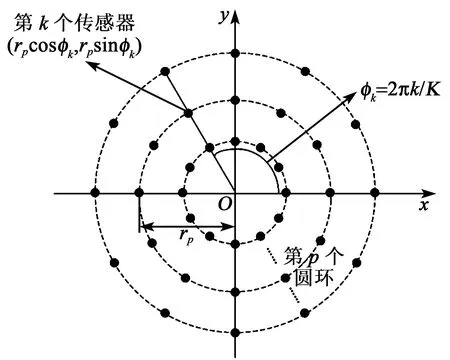
图1 UCCA结构图
现假设信号与阵列处于同一平面,则第(k,p)个传感器的输出信号为
(1)
式中:f为信号的频率;φ为近场宽带信号s(t)的方位角;ρ为信源与阵列中心的距离;S(f)为s(t)的频率响应;c为信号波的传输速度。
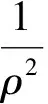
(2)

(3)
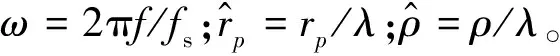
每个圆环上的输出信号经离散傅里叶逆变换(IDFT)转换成相位模式信号,第p个圆环上的第m路相位模式信号为
(4)
式中m=-M,-M+1,…,M,M=(L-1)/2,L≤K是每个环上的相位模式总数,本文取L为奇数。L为偶数时与文中方法类似。
为了修正近场畸变,本文在每个相位模式信号上采用一个矫正系数gm,p对其进行矫正。如图2所示,各圆环上经矫正后具有相同阶数m的相位模式信号相加后,通过频率补偿网络Hm(ω)来消除宽带阵列响应的频率依赖性。最后,经过近场矫正和频率响应补偿的信号乘上波束形成权系数wm并求和,即可得到波束形成器的输出信号。综上,波束形成器输出的频率响应为
(5)
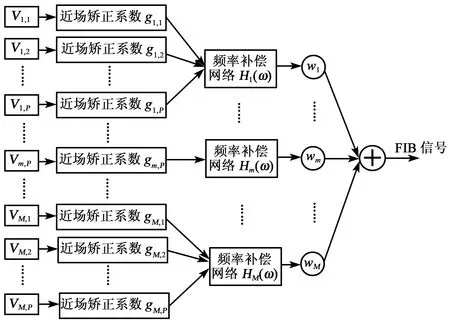
图2 FIB原理图
将式(3)、(4)代入式(5),得到阵列输出为
(6)
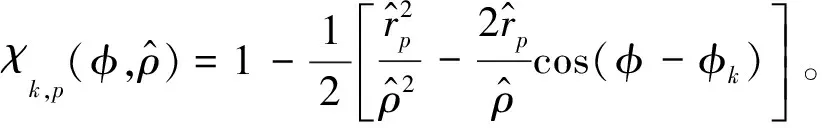
(7)

式(7)可近似为
(8)
由式(8)可看出,通过选择合适的gm,p和Hm(ω),可使
(9)
则式(8)可等价为
(10)
由式(10)可知,本文设计的UCCA时空响应可达到近似频率不变。此外,该阵列的波束图仅由波束形成加权系数wm决定。因此,该阵列中的补偿网络可以离线设计,而波束模式可进行自适应调整,故算法复杂度大幅降低。
gm,p和Hm(ω)可通过凸优化理论设计。假设补偿滤波器在频率ω0处有Hm(ω0)=1。此时,由式(8)可知,设计近场矫正系数即是找到gm,p,使
(11)
其中:
(12)

频率补偿网络主要由一个长度为LF的滤波器组成。第m个相位模式滤波器的冲激响应记为hm≜[hm1,hm2,…,hmLF-1],则滤波器的频率响应为
(13)
式中ei≜[1,e-jωi,…,e-j(LF-1)ωi]T。频率补偿网络的设计思路就是找到hm满足:
(14)
其中:
(15)
式中:ωi∈(ωL,ωU);Nω为频率取样个数。
式(11)、(14)均可以转换成二阶锥规划(SOCP)问题,因而可以通过凸优化工具快速地求解[10]。
2 近场UCCA-FIB的自适应波束形成
利用第1节提出的近场UCCA-FIB,本节研究其自适应波束形成方法,即wm的设计。假设期望信号S(ω)以方位角φs到达阵列,同时有干扰信号I(ω)以方位角φI到达阵列,利用式(1),阵列第p个圆环上的输出可写成
(16)

(17)

(18)
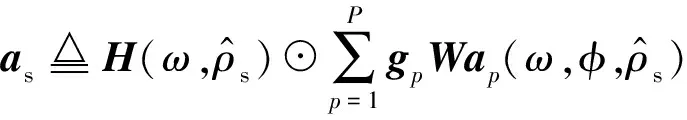
(19)

由式(19)可知,本文提出的近场UCCA-FIB的输出相当于一个远场均匀线性阵列。因此,传统的自适应波束形成算法可以推广到该阵列中。根据式(19),对每路相位模式信号进行波束形成加权并求和,则可得到波束形成的输出信号
(20)
式中w≜[w-M,w-M+1,…,wM]T为波束形成权重向量。该向量可通过最优化输出信号的信干噪比(SINR)得到,其优化模型为
(21)

(22)
在实际计算过程中,一般使用样本协方差矩阵代替干扰噪声协方差矩阵计算,即
(23)
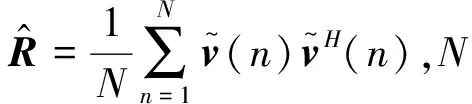
3 仿真结果
为了验证本文提出的近场宽带阵列的性能,本节设计了一个UCCA-FIB以及基于此而设计的SMI波束形成方法。在本文的设计例子中,阵列由两个圆环组成,即P=2,每个圆环上有12个天线或传感器,即K=12。相位模式的个数L=9,研究的频段为ω∈[0.35π,0.5π],ρ=20λ。在第一个例子中,考察UCCA-FIB的频率响应不变特性和近场矫正效果,为简单起见,取波束形成权向量为w=[1,1,…,1]T。根据第1节中的设计方法得到近场矫正系数和频率补偿网络,阵列的波束图如图3所示。由图可看出,本文提出的宽带近场UCCA-FIB在目标频段近似频率不变。
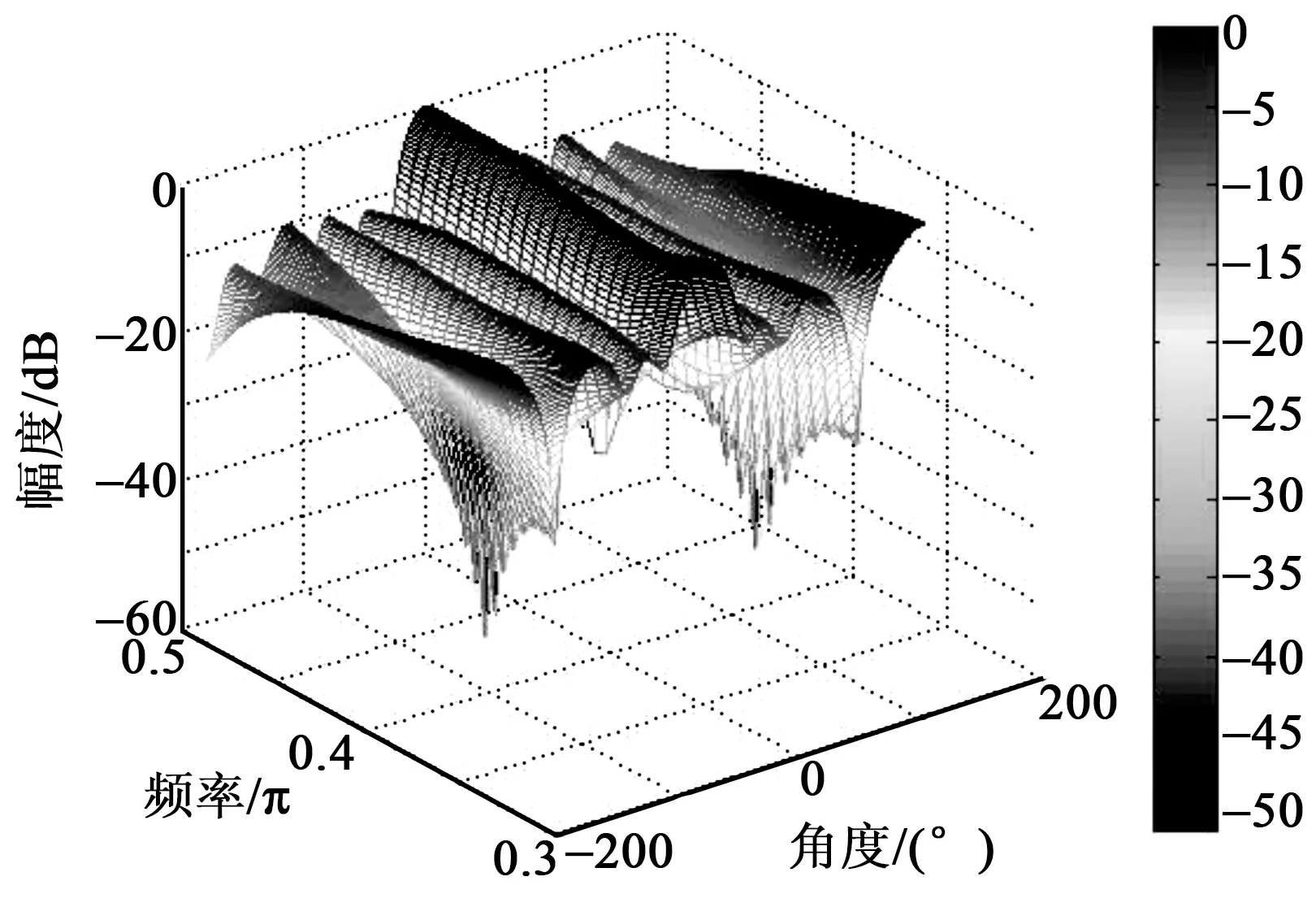
图3 近场FI-UCCA的波束方向图与ω的关系
图4为有无近场矫正时的波束图。由图可见,经近场矫正后的阵列响应具有更低的旁瓣,实现了近场矫正。

图4 有无近场矫正的波束图对比
在本文第二个例子中,使用第一个例子中设计的近场UCCA-FIB来评估波束形成的性能。设期望宽带信号以φs=0°到达阵列,与同心圆阵中心的距离ρs=20λ。同时假设干扰信号的入场方位角φI=80°,与同心圆阵中心的距离ρI=25λ。假设输入信噪比为0,干噪比(INR)为20 dB。使用近场UCCA-FIB进行波束形成的输出SINR随着输入信噪比(SNR)的变化情况如图5所示。同时,图5还给出了无近场矫正UCCA-FIB和TDL的波束形成性能。由图可见,使用近场UCCA-FIB进行波束形成后,与其他两种方法相比,输出SINR有明显改善。
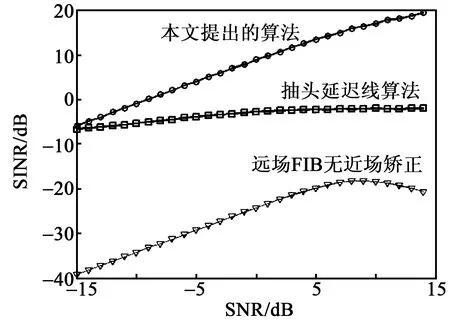
图5 波束形成性能比较
4 结束语
本文介绍了一种均匀同心圆阵频率响应不变的近场宽带波束形成器设计方法。该方法利用近场矫正系数修正了近场效应,采用频率补偿网络消除了阵列响应的频率依赖性,将近场宽带阵列的波束形成问题转化为远场窄带阵列波束形成问题。因此,绝大部分传统窄带波束形成方法可以应用到本文提出的近场宽带阵列中。仿真结果表明,本文提出的近场同心圆阵列算法可行,做到了频率响应不变的要求。与其他近场宽带波束形成方法相比,同心圆阵列在波束形成方面具有更好的性能。

