桩后-桩侧共同成拱的悬臂式抗滑桩合理桩间距研究

林 之 航

(福州市规划设计研究院， 福建 福州 350108)

作为一种大截面、大刚度的柱形构件，抗滑桩可将滑体的下滑力传递到滑床深部的稳定地层，已被广泛应用于大、中型滑坡的治理工程之中[1-3]。其中，抗滑桩设计的关键在于桩间距的合理确定，以便充分利用桩后的土拱效应达到经济合理的目的。

关于合理桩间距计算的研究，先前学者已从不同角度开展了大量研究。陈龙等[4]根据土拱的极限平衡条件，推导出土拱间的相互作用力与合理桩间距的计算公式。周德培等[5]、胡晓军等[6]、周应华等[7]则以桩间静力平衡条件、拱脚或跨中截面强度条件来确定合理桩间距。蒋良潍等[8]将黏性土土拱计算的平衡条件和强度条件简化为以拱脚处拱圈轴向压应力表达的形式，利用摩尔-库仑强度准则推导了桩间距上下限的简便计算式。肖世国等[9]则假定桩后两侧土拱受压区形状为梯形，令桩间土拱满足桩间静力平衡条件、强度条件以及桩土变形协调条件，藉此给出了合理桩间距的计算公式。

但是，上述研究多基于平面条件，即忽略了土体自重应力对其土拱形成及稳定性的影响。事实上，桩间及桩后土体均为三向受力状态，基于平面条件的假设难以准确描述实际工程问题。为此，黄治云[10]基于Drucker-Prager破坏准则推导了考虑自重应力的合理桩间距计算公式。李长冬等[11]则基于统一强度理论构建了三维多层滑坡体中抗滑桩桩间距的计算模型。但有必要指出的是，前者在考虑自重应力(亦即中主应力)的作用时，又简单的认为第三主应力σ3为零，也即是未考虑桩侧成拱；后者则依据桩间距的大小认为桩后土拱与桩侧土拱分别独立的存在。但当前大量研究却表明抗滑桩桩后土拱和桩侧土拱同时存在并共同承担滑坡推力[12-15]。

鉴于此，本文首先构建了桩后-桩侧土拱共同作用的平面概化解析模型，并基于拱体静力平衡条件、土体成拱强度条件确定了考虑自重应力作用的桩后-桩侧土拱的极限应力状态。然后借助经典的Drucker-Prager强度破坏准则提出了考虑桩后-桩侧土体共同成拱的合理桩间距计算方法。最后在此计算模型的基础上，探讨了滑坡体抗剪强度、滑坡推力等重要设计参数对抗滑桩合理桩间距的影响。

1 计算模型

1.1 基本假定

抗滑桩的土拱效应即为桩后或桩侧土体在滑坡推力或土压力的作用下产生不均匀变形，引起应力的重新分布，表现为将作用于拱后的滑坡推力传递到拱脚及周围稳定介质中去[16]。鉴于土体自身力学特性及桩-土相互作用的复杂特性，为简化计算，本文做出如下假定：

(1) 假定桩后滑坡推力沿桩间跨度方向水平均匀分布，且仅考虑抗滑桩截面为矩形的工况。

(2) 桩后及桩侧土拱同时存在并共同承担桩后滑坡推力，如图1所示，且假定桩后滑坡推力沿桩间均匀分布。

(3) 假定抗滑桩为刚体，忽略其自身变形。

图1 桩后-桩侧共同成拱模型示意图

图2即为根据上述假设所确定的桩后-桩侧土拱共同作用下的合理桩间距平面概化计算模型示意图，其中L为抗滑桩桩间距，A为抗滑桩桩侧截面宽度，B为抗滑桩桩正截面宽度。

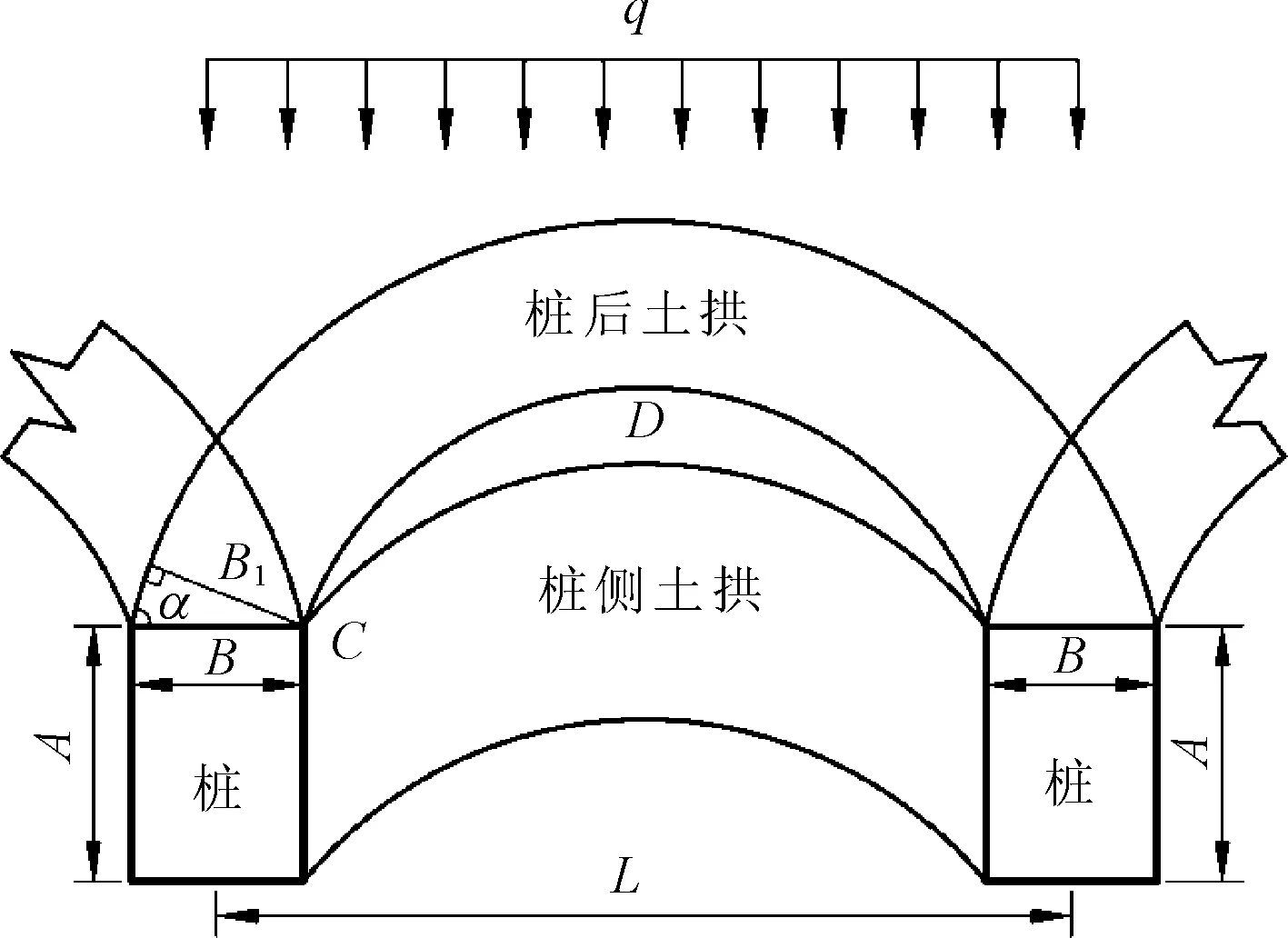
图2 桩后-桩侧土拱平面概化模型

1.2 合理拱轴线

由于拱体组成介质与前后岩土体基本相同，表现为拱体与前后岩土体之间无明显界线[17]，此时，可借助拱轴线予以定量分析。事实上，土拱形态即为应力偏转所形成的偏转路径，即受荷后土体产生不均匀位移以调动自身抗剪强度抵抗外力而自发形成土拱，土体中最大主应力方向的迹线即为“合理拱轴线”[17]。在均匀滑坡推力作用下，相应的合理拱轴线方程可采用二次抛物线来表示：

y=ax2+bx

(1)

式中：a、b为拱轴线方程参数，其中a=-4f/L2，b=4f/L，f为桩后土拱的拱矢高。

图3即为简化的土拱合理拱轴线计算模型,在均布荷载q作用下，由桩后土拱拱体的静力平衡条件可确定拱脚处反力Fx、Fy分别为：

(2)

(3)

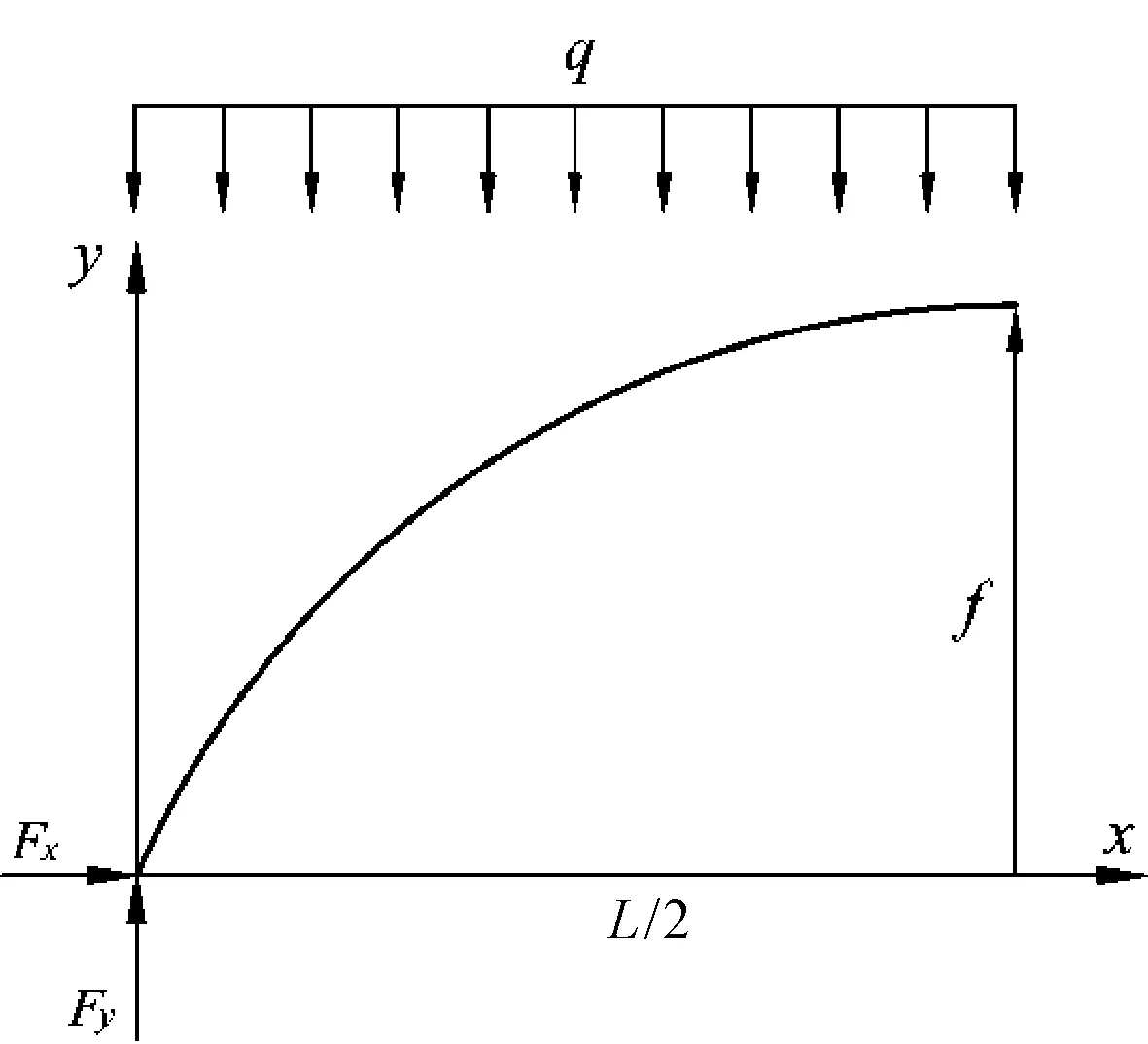
图3 合理拱轴线计算模型

2 桩后-桩侧共同成拱

2.1 桩后受荷成拱

为保证桩后土拱正常发挥作用，防止土拱发生破坏从桩间滑出，需满足桩后静力平衡条件，即拱脚破坏面上的侧摩阻力不小于滑坡体推力在水平面上的分力，极限状态时可表示为：

(4)

式中：φ为滑坡土体内摩擦角；c为滑坡土体黏聚力；B1为土拱厚度。

由结构力学知识可知，拱脚处的轴力最大。此时，取单位厚度土拱，即可确定拱脚处的最大轴向应力为：

(5)

另一方面，为方便计算拱轴线方程参数b，可根据单向受压状态的莫尔-库仑准则，即

(6)

将式(4)～式(6)联立，并注意到Fx=qL2/8f，b=4f/L,即可获得拱轴线方程参数b。

(7)

显然，由式(7)可知，拱轴线方程参数b仅与土体内摩擦角有关，表明桩后土拱的拱轴线方程参数与桩侧土拱的相同。

2.2 桩侧摩擦成拱

抗滑桩桩侧土拱同样具有一定的承载能力，因此考虑桩后及桩侧土拱效应共同作用能较准确的反映工程实际情况，进而准确的确定桩间距。

鉴于桩侧成拱机制与桩后成拱机制基本相同，同样假设其合理拱轴线为二次抛物线。当桩侧土拱单独作用时，其桩侧土拱的拱脚受力分析如图4所示。根据拱体的静力平衡条件，桩土界面的反力可表示为：

(8)

(9)

式中：Fx2为桩侧土拱拱脚处的水平反力；Fy2为桩侧土拱拱脚处的竖向反力；q2为桩侧土拱极限承载均布荷载；f2为桩侧土拱拱矢高；l为桩间净距。

同样，为保证桩侧土拱正常发挥作用，防止拱体从桩间剪出，需满足桩间静力平衡条件，即拱脚破坏面上的侧摩阻力不小于破体推力在水平面上的分力，当取极限状态时可得等式为：

(10)

式中：A为桩侧截面宽度;c2为桩侧土体与桩间的黏聚力；φ2为桩侧土体与桩接触面的内摩擦角。桩侧为岩石或岩块时取φ2=φ/2，为细粒土时取φ2=φ/2或φ2=2φ/3；而c2可取c2=ctanφ2/tanφ[6]。

将式(8)与b=4f2/l带入式(10)可得桩侧土拱的极限承载力：

(11)

图4 桩侧土拱计算模型

3 合理桩间距的确定

3.1 临界应力状态的确定

有关抗滑桩的先前研究表明，当桩间距设置过大时，土拱最有可能在拱脚或拱顶处发生破坏[5,7,18]。为此，现分别对拱脚和拱顶两处进行强度验算以确定合理桩间距。

首先，确定拱脚与拱顶处的应力状态。拱脚C处的大主应力实质上即为拱脚处的轴力除以土拱截面面积：

(12)

其中，拱体厚度B1可根据图2中的几何条件表示为：

B1=B·sinα

(13)

又合理拱轴线在原点处的切线斜率与拱轴线方程参数b的关系可表示为：

(14)

且有三角函数万能公式：

(15)

(16)

联立式(14)—式(16)可得：

(17)

将式(17)代入式(13)可得拱体厚度为：

(18)

另一方面，研究表明土拱跨中截面处的前缘点较后缘点更易破坏[7]，取跨中截面前缘点D验算其强度需求。

则该点处的最大主应力可表示为：

(19)

令土体自重应力为中主应力，即土拱拱脚处与土拱跨中截面前缘点处的中主应力为：

σ2=γz

(20)

式中：γ为土体重度；z为距坡顶坡面的距离。

当桩间距布设合理时，桩侧土拱与桩后土拱共同承担来自桩后滑体的推力，此时，桩侧土拱可给予桩后土拱一定的支撑力。且桩侧所能承受的最大均布荷载相对于桩后土拱的最大主应力较小，可简单的将桩侧土拱的极限承载力q2近似为第三主应力，则土拱拱脚处与土拱跨中截面前缘点处的第三主应力可表示为：

(21)

至此，拱脚与拱顶处的临界应力状态均已确定。

3.2 强度控制条件

Drucker与Prager于1952年提出的考虑静水压力影响的广义Mises屈服与破坏准则[19]特别适用于岩土类材料，其所需参数极少，且可由摩尔-库仑准则材料常数换算。Drucker-Prager强度准则可用如下函数表示：

(22)

式中：I1=σ1+σ2+σ3为应力张量第一不变量；

J2=[(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]/6为应力偏量第二不变量；其中α，k为Drucker-Prager破坏准则材料常数，其与土体抗剪强度参数c，φ之间的关系如下：

(23)

现基于Drucker-Prager破坏准则作为强度控制条件来验算拱脚和拱顶处的稳定性，进而推导出考虑桩后-桩侧成拱与自重应力作用下的合理桩间距。

将式(22)整理为关于第一主应力σ1的方程：

(24)

式中：D2=3α2-1，E2=6αkσ1+6α2(σ2+σ3)+σ2σ3；F2=3k2σ12+6αk(σ2+σ3)+(3α2-1)(σ22+σ32)+(6α2+1)σ2σ3

求解可得：

(25)

进而，土拱拱顶和拱脚处的临界应力状态代入式(25)，整理即可获得一定推力下拱脚强度控制与跨中截面强度控制的合理桩间距：

(26)

(27)

对比分析式(26)与式(27)可知：

(28)

显然有LD>LC,表明一旦桩间距增大，拱脚将先于拱顶发生破坏，这与先前学者通过试验研究和计算分析所得研究成果相一致[18,20-21]。也即是说，基于拱脚强度控制所得桩间距则为合理桩间距。同时，值得注意的是，由于式(26)中包含了自重应力项，则其必为土拱埋深z的函数，则最终所确定的合理桩间距可表示为：

Lopt=minLC

(29)

至此，一旦具体工程中的滑坡推力与滑坡土体参数已知时，即可借助MATLAB对上式进行迭代计算，藉此确定该工程的合理桩间距。

4 合理性验证与分析

4.1 工程实例的可行性验证

4.1.1 实例一

选取文献[9]中的工程实例予以对比分析。四川北部某高速公路堆积体路堑高边坡，其最下一级边坡采用悬臂式抗滑桩予以支护，如图5所示。桩后滑体的平均重度γ=20 kN/m3，快剪强度参数中黏聚力c=50 kPa，内摩擦角φ=28°。抗滑桩全长h=22 m，其中悬臂段长度z=11 m；且抗滑桩桩侧截面宽度A=3 m，桩正截面宽度B=2 m。由荷载传递法所得桩后坡体推力E=1 050 kN/m。该工程实际桩间距取值为6.0 m，工程完工后坡体稳定性状况良好。

首先，作用于单位高度土拱上的桩后坡体平均压应力q=E/z=1050/11=95.45 kPa。然后，将上述工程参数带入式(7)、式(18)、式(26)中，即可确定距桩顶不同深度的抗滑桩合理桩间距Lopt=8.80 m。

但值得注意的是，本文所推导的合理桩间距是基于桩后-桩侧土拱处于极限平衡状态，为确保土拱的稳定性，还需考虑一定的安全储备[22]，建议安全系数取1.3～1.5，则对应的合理桩间距取值区间为L∈[5.87,6.77]。通过与该工程实际桩间距取值进行对比，表明本文所提方法有一定的指导意义。

为进一步验证本文方法的合理性，针对该工程实例，采用先前学者所提方法来计算抗滑桩桩间距，汇总如表1所示。与此同时，表1还给出了各方法在进行桩间距推导过程中所存在的部分问题。由表1可知，不同方法所得计算结果相差较大，其原因一方面在于考虑的因素不同，另一方面，在于采用的强度判定准则不同。但总体趋势表现为，考虑桩后土拱土体的自重应力或桩侧土拱的作用所得的合理桩间距大小有一定程度的增加，因为这些因素有利于桩后土拱的稳定和土拱效应的发挥。而本文方法虽经一系列简化，但考虑了桩后-桩侧共同成拱和土拱土体自重应力的作用，因此所得桩间距大小更符合实际情况。

图5 工程实例示意图

表1 相关文献方法与本文方法的桩间距计算值(实例一)

4.1.2 实例二

本实例主要以滑体抗剪强度较弱的工况为对象，以验证本文公式在小截面抗滑桩设计中的适用性。选取文献[7]中的工程实例，该滑坡位于四川省泸州市世寿街沱江下游河口段右岸，体积为10.32×104m3，工程布设处滑动面埋深10 m。滑体组成物质主要为粉质粘土，雨季土体含水量较高，呈软塑的下限状态，其抗剪强度参数为c=28 kPa，φ=8°。滑体设计推力为300 kN/m。拟选用抗滑桩予以治理，桩体截面尺寸为0.9 m×0.9 m。

首先，确定作用于单位高度土拱上的桩后坡体平均压应力为：q=E/z=300/10=30 kPa。同样，将上述工程参数代入式(7)、式(18)、式(26)中，即可确定该抗滑桩的合理桩间距为2.52 m，安全系数取1.3～1.5，则对应的合理桩间距取值区间为L∈[1.68,1.94]，而该工程的实际设计时的桩间距取1.8 m。显然，本文方法也适用于小截面抗滑桩的设计。

同样，采用先前学者所提方法来计算抗滑桩桩间距，汇总如表2所示。由表2可知，各方法所得的桩间距大小整体上相差不大。但通过对比发现，当桩后滑体抗剪强度较弱时，相较而言，桩侧土拱对合理桩间距的影响较小，而土体自重应力则对其影响较为显著(如从文献[6]所得的2.04 m增至文献[8]所得的2.83 m)。这也进一步说明了基于桩后土拱效应建立的抗滑桩合理桩间距的计算方法有必要考虑桩后土体自重应力的作用。

表2 相关文献方法与本文方法的桩间距计算值(实例二)

4.2 合理桩间距影响因素分析

为综合研究设计参数对抗滑桩合理桩间距的影响，利用上述所建立的考虑桩后-桩侧共同成拱和自重应力作用的合理桩间距计算公式，探讨了桩后土体强度参数(黏聚力c，内摩擦角φ)、滑坡推力q以及桩截面尺寸(包括截面侧面宽度A和正面宽度B)等关键参数的影响。

4.2.1 土体抗剪强度参数的影响

图6给出了土体强度参数与合理桩间距的关系。由图6可知，土体黏聚力与土体内摩擦角对合理桩间距的影响一致，即合理桩间距均随黏聚力与内摩擦角的增大呈近似线性增大， 表明土体抗剪强度参数对桩后土体的成拱效应具有关键作用。当然这也主要是由于土拱效应的应力传递是通过土体抗剪强度的调用来实现的[7]，因此较大的土体抗剪强度参数有利于桩后土拱效应的形成。反过来讲，当桩后土体的抗剪强度降低时，桩后成拱所需的桩间距亦随之减小。否则，桩间土体就有可能发生失稳，这也即是降雨期间桩间土最易发生垮塌、局部失稳等不良地质灾害的原因。

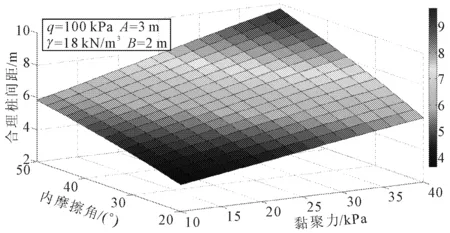
图6 抗剪强度参数与合理桩间距的关系

4.2.2 拱后滑坡推力的影响

图7为滑坡推力与合理桩间距的关系图。由图7可知，合理桩间距随拱后滑坡推力增大而逐渐减小，减小趋势逐渐趋于平缓。同时，合理桩间距的大小亦随着桩后拱体埋深的增加而增加，这是由于随着拱体埋深的增加，拱体所受围压也随之增加，相应的其抗剪强度也显著增强，致使维持桩后与桩侧土拱土体稳定所需的桩间距随之增加。同时，这也如实反映了实际工程中抗滑桩桩间土的失稳破坏多发生于悬臂段上部土体的原因。因此，若在设计中忽略桩后拱体自重应力的影响，则使抗滑桩桩间距的设计偏于保守。

图7 滑坡推力与合理桩间距的关系

4.2.3 桩截面尺寸的影响

抗滑桩截面尺寸直接为拱脚提供支撑力，图8为桩截面尺寸与合理桩间距的关系图。

图8 桩截面尺寸与合理桩间距的关系

由图8可知，抗滑桩的合理桩间距随桩正截面宽度与桩侧截面宽度增大而增大。相较而言，桩正截面宽度对合理桩间距的影响较桩侧截面宽度影响大。这主要是由于桩正截面为桩后土拱提供支撑力，桩侧截面通过摩阻力为桩侧土拱提供支撑力，而滑坡推力主要由桩后土拱承载传递到周围稳定介质中去，这与Li等[24]和林治平等[25]基于数值模拟所得结果相一致，即桩后土拱分担的滑坡推力大于桩侧土拱，占主导地位。

5 结 论

(1) 依托两典型工程实例，并将本文计算所得抗滑桩桩间距与前人研究成果进行了对比，结果表明本文方法可较准确的确定抗滑桩的合理桩间距，且表现出较好的适用性。同时，由于本文所提方法是基于土拱处于极限平衡状态，为确保其稳定性，还需考虑一定的安全储备。

(2) 抗滑桩合理桩间距随桩后拱体抗剪强度参数的增加而近似呈线性增加，又随滑坡推力的增大逐渐减小并趋于平缓。同时，合理桩间距的大小随桩后土拱埋深的增加而逐渐增加，若忽略桩后拱体自重应力的作用，则所得结果将偏于保守。相较于桩侧面宽度，桩正截面宽度对合理桩间距的影响更为明显。