关联帷幕防渗性能变化的重力坝结构稳定评价方法

彭 琦，高大水，高江林，张宇驰

(1.长江勘测规划设计研究有限责任公司， 湖北 武汉 430010；2.江西省水利科学研究院， 江西 南昌 330029)

重力坝是水库大坝广泛常用的坝型，重力坝稳定主要靠自重保持，坝基扬压力方向与坝体重力方向相反，是不利于坝体稳定的荷载，对大坝稳定影响也较大[1-2]。1895年，法国坝高22 m的布泽(Bouzey)重力坝因设计时未考虑坝基扬压力作用而失事，随后几十年也有重力坝因坝基劣化导致扬压力增大而发生破坏[3]，逐渐引起国内外学者对扬压力的重视和研究。工程上一般采用坝基帷幕灌浆结合排水孔措施，减小坝基扬压力，提高大坝稳定安全性，在对新建重力坝稳定计算时，常规方法按有无新设防渗帷幕和排水孔，取折减系数乘以上下游水头差计入扬压力，采用抗剪或抗剪断力学方法进行大坝结构稳定计算，并采用材料力学方法进行坝基应力计算[4-7]。常规方法适用于新建重力坝结构稳定计算，但对经长期运行的水库大坝，受库水渗压和化学侵蚀，坝基帷幕防渗性能发生衰变，进而影响大坝稳定，按常规方法取折减系数计入扬压力进行结构稳定计算会产生较大误差[8-9]，需要分析坝基帷幕防渗性能变化对扬压力的影响，进一步研究关联帷幕防渗性能变化的结构稳定评价指标和方法。

1 坝基帷幕防渗性能对扬压力的影响分析

为了解坝基帷幕防渗性能变化对扬压力的影响，以某水库砌石重力坝为例建立有限元计算模型(见图1)，并选取正常蓄水位工况，以达西定律和渗流连续性方程为理论基础进行数值计算分析[10-15]。

图1 砌石重力坝三维模型

模型包括坝体和坝基，坝体分区包括砌石体、防渗面板、混凝土基础，坝高44 m，坝顶宽8 m，下游坝面下部坡比1∶0.7；坝基分区根据岩石风化程度和透水性分上、下两层基岩，并设置有防渗帷幕。

根据地质勘察钻孔压水试验及类似工程经验确定模型参数(见表1)，其中帷幕防渗系数k3作为变量，分别选取k3=(2+0.5i)×10-5cm/s，其中i=0,1,…，13,14。水库正常蓄水位时上游水头40 m，下游水位按基本无水考虑。分别计算得到正常蓄水位工况帷幕不同渗透系数时坝基帷幕中心线处O点的扬压力(压力水头值)，绘制该点压力水头值-帷幕渗透系数关系曲线图(见图2)，随着坝基帷幕防渗性能衰减，其渗透系数增大，压力水头也相应增大，随着帷幕渗透系数逐渐接近所在基岩渗透系数，其增速由快变慢，直至完全失效而无法再起到防渗作用。计算提取其中帷幕基本完好时k3=2×10-5cm/s的坝基扬压力分布(见图3)，可见坝基帷幕起到了减小扬压力作用，随着帷幕防渗性能衰减而渗透系数增大，坝基帷幕中心线处O点扬压力也会相应增大，进而将影响大坝稳定安全。

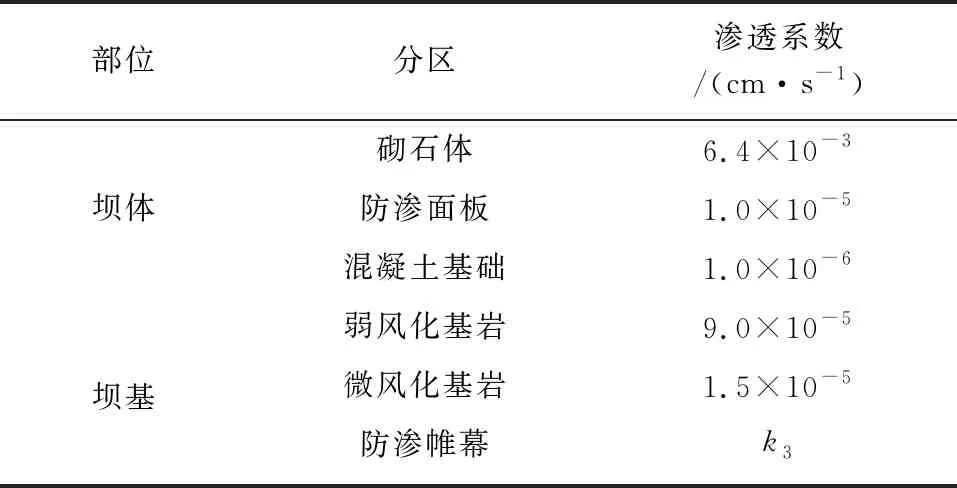
表1 计算模型各材料分区渗透系数表

图2 坝基帷幕处压力水头与帷幕渗透系数关系曲线

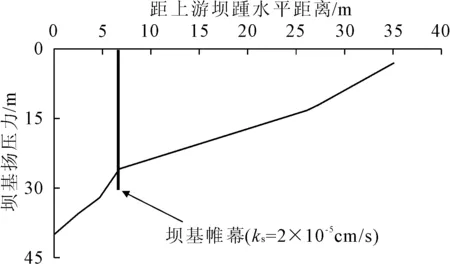
图3 坝基扬压力分布图

由以上分析可知，坝基帷幕防渗性能的变化对扬压力的影响明显，压力水头值与帷幕渗透系数之间为非线性增长关系，不同的帷幕渗透系数对应不同的压力水头值，即对应不同的折减系数，因此，帷幕防渗性能发生衰减变化时，扬压力折减系数相应变化，会影响大坝结构稳定。

2 关联帷幕防渗性能的结构稳定评价指标

2.1 评价指标函数

重力坝结构稳定受坝基帷幕防渗性能的间接影响，对重力坝结构稳定安全评价时，需考虑帷幕防渗性能的变化。以抗剪或抗剪断稳定计算公式为基础，引入帷幕渗透系数参数，建立结构与渗流的关联函数。进一步对前述砌石重力坝计算模型进行有限元计算分析，分析防渗帷幕渗透系数与抗滑稳定及坝基应力的结构渗流相关性，得到帷幕渗透系数k3与坝基抗滑稳定系数K(抗剪稳定系数)、K′(抗剪断稳定系数)的关系，并拟合绘制相关曲线(见图4和图5)，同时得到帷幕渗透系数与坝基垂直正应力的关系，绘制相关曲线(见图6和图7)。

图4 坝基抗滑(抗剪)稳定系数-帷幕渗透系数关系曲线

图5 坝基抗滑(抗剪断)稳定系数-帷幕渗透系数关系曲线

图6 坝基上游面垂直正应力-帷幕渗透系数关系曲线

图7 坝基面下游面垂直正应力-帷幕渗透系数关系曲线

令k3=k×10-5cm/s，分析得到分别基于抗剪和抗剪断公式的坝基抗滑稳定系数-帷幕渗透系数关系函数(见式(1)和式(2))，并分别得到坝踵和坝趾垂直正应力-帷幕渗透系数关系函数(见式(3)和式(4))。

K=0.0082k2-0.1362k+1.5071

(1)

K′=0.0082k2-0.1362k+3.3171

(2)

(3)

(4)

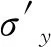
2.2 实例计算

3 关联帷幕防渗性能的结构稳定评价步骤

(1) 收集有关工程资料及参数。首先需收集重力坝有关的设计、施工、质量检测与安全监测等资料，必要时需补充进行试验检测，包括钻孔取芯和压水试验等，以获取重力坝坝体结构与坝基岩体的物理力学指标和渗透系数，对收集到的资料和试验成果进行综合分析，尽可能准确客观地确定坝体和坝基各分区的参数。

(2) 建立重力坝有限元计算模型。选取典型坝段或坝体单宽断面建立三维或二维有限元计算模型，一般选取坝高最高坝段或地质条件最不利坝段作为典型坝段，适当简化后保留主要结构分区，并输入分区计算参数，建立重力坝有限元模型。模型中地基深度应超过帷幕深度两倍，坝踵上游长度和坝趾下游长度应不小于两倍坝高；模型单元剖分精度应合理确定，在计算机运算速度满足效率要求前提下适当精细[7]。

(3) 渗流计算并根据监测资料修正模型。根据实际运行条件确定重力坝的计算工况和水位，采用有限元热分析模块模拟进行渗流计算，得到各工况的渗流场分布，进而提取监测点位置节点的水头计算值，并与相应监测点的渗压水头实测值进行对比，若计算值与实测值吻合，说明模型及参数整体上是合理的，若计算值与实际值存在明显差异，应分析原因并对模型相应分区参数进行适当调整，反演试算后确定最终分区参数，使计算模型符合和接近实际情况。

(4) 建立结构稳定与帷幕防渗参数关系。通过有限元计算得到重力坝坝基扬压力分布，进而按照抗剪公式和抗剪断公式计算得到的坝基面抗滑稳定系数；有限元计算还可分别得到相应计算工况坝基上游坝踵和下游坝趾的垂直正应力；按此方法将坝基帷幕灌浆渗透系数作为变量，选取帷幕灌浆不同渗透系数，并计算对应的抗滑稳定系数和坝基应力，采用曲线拟合统计方法得到重力坝结构稳定与帷幕防渗参数关系曲线，分析得到结构稳定系数与应力的曲线拟合函数。根据坝基实际压水试验得到帷幕渗透系数，代入关系函数便可直接计算得到大坝的稳定安全系数和坝基应力。

(5) 求解帷幕渗透系数容许值并判别结构稳定。根据重力坝建筑物级别和运行工况组合，按有关设计规范要求可查得结构稳定及应力规范值，将规范值代入前述曲线拟合函数中，反算求解得对应的防渗帷幕渗透系数计算值，将其小值作为满足结构稳定与应力要求的帷幕渗透系数容许值。将此容许值作为判别评价结构稳定的直接指标，当帷幕渗透系数小于等于该容许值时，可认为大坝稳定安全；当帷幕渗透系数大于该容许值时，可认为大坝稳定不安全。

4 结 论

(1) 重力坝坝基帷幕随着运行时间增长，帷幕防渗性能在库水渗压和化学腐蚀作用下会逐渐衰减，坝基扬压力随帷幕渗透系数增加而增加，扬压力折减系数相应增大，会影响大坝结构稳定。

(2) 坝基扬压力与帷幕渗透系数呈非线性增长关系。随着帷幕渗透系数逐渐接近所在基岩渗透系数，扬压力增速由快变慢。

(3) 通过模拟建立重力坝模型并采用有限元计算分析，可建立重力坝结构稳定应力与帷幕渗透系数的关系函数，形成关联帷幕防渗性能变化的重力坝结构稳定应力计算方法；采用此方法已知帷幕渗透系数即可直接计算得到大坝的稳定安全系数和坝基应力。

(4) 采用关联帷幕防渗性能变化的结构稳定计算方法，可反算求解得到防渗帷幕的最小渗透系数，即为满足大坝稳定要求的帷幕渗透系数容许值，将此作为帷幕防渗性能衰减对大坝稳定影响评判的依据，可对重力坝结构稳定安全进行更加客观和准确的评价。