富水岩质隧道开挖稳定性分析

侯云乾，张 泽，朱宝强，王 锋，杨 伟，魏云龙，李志军，王述红

(1.中交隧道工程局有限公司，北京 100020; 2.东北大学 资源与土木工程学院，辽宁 沈阳 110819)

目前我国正处于基础建设的高速发展时期，全国各个地区的隧道建设都在如火如荼的开展。随着各地不同地区隧道的建设，工程中会受到地形条件限制以及遇到各种复杂的地质情况[1]。大断面小净距隧道耦合富水软弱围岩的地质条件[2]，会引起围岩稳定性差、左右侧隧道开挖和中间岩体相互影响，易引发突水、突泥、塌方、大变形等灾害，这是复杂的围岩应力场与渗流场耦合作用问题。在2004年我国首次定义了公路隧道中的小净距隧道：规定中间岩柱厚度小于1.5倍隧道开挖宽度的分离式独立双洞隧道[3]。与分离式隧道相比，小净距隧道克服了隧道在展线以及洞外接线的问题；与联拱隧道相比，其造价更低，施工更简单并且容易控制施工质量。由于小净距隧道两平行双洞间距离较小，先行洞与后行洞的开挖势必会对中岩柱造成多次扰动，而中夹岩作为小净距隧道稳定性最重要的部位势必会对整个隧道的安全性产生重要的影响[4-6]。对于下穿富水围岩隧道的稳定性问题，国内外学者进行了大量研究并取得了一些成果，然而对于小净距隧道穿越富水围岩的稳定性研究却很少[7]。 张雨凡等[8]小净距隧道的滞后距离进行了研究，采用ANSYS进行模拟计算，但其只对竖向位移和承受荷载进行了分析，并没有考虑中夹岩处的水平位移。王晓杰等[9]和Shi[10]以青岛地铁2号线下穿地铁1号线的工程为背景，对小净距立体交叉隧道进行流固耦合数值模拟与试验相结合的方法进行研究，结果表明开挖是隧道变形增大的主要原因，但是没有对中间部分的位移进行研究。Chapman等[11]通过室内试验对土中临近隧道的施工过程进行研究，并获得两条隧道相互扰动的蠕变效应。

本文以重庆在建花阳隧道为背景，基于流固耦合理论和小净距隧道开挖理论，针对富水区域小净距隧道开挖后的力学行为进行分析。

1 有效应力原理和渗流本构关系

1.1 有效应力原理

(1)

比奥系数可以根据Geertsma提出的下式求得：

(2)

式中：E是岩石的体积模量,GPa；Es是岩石固体颗粒的基质体积模量,GPa。在两个不同的实验中测量岩石的体积模量和岩石的基质体积模量。在第一个实验中，通过将孔隙压力设为零来获得E；在第二实验中，Es是通过将孔隙压力和围压设定为相等而获得的。

通常Es>E，Hashin认为材料在微观和宏观上都是各向异性，从而获得下式：

(3)

因此可以推出新的应力应变关系：

(4)

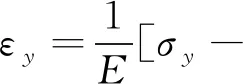
(5)

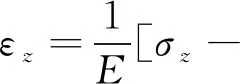
(6)

(7)

(8)

(9)

1.2 流固耦合控制方程

本构方程包括平衡方程，力学行为和根据Biot概念的有效应力定律以及结合了达西定律和流体质量守恒的流体扩散方程表示。

1856年，亨利·达西(Henry Darcy)研究了与喷泉有关的垂直均质砂滤器中水的流动情况。从他的实验研究中，定义了流量q与恒定横截面积A和液压头差(h1-h2)成正比，与两个液压头L的距离成反比为：

(10)

其中K是水力传导率。水力传导率通常在水文地质学中使用[6]，是衡量特定流体通过特定土壤材料的难易程度的一种度量。此外，式(11)给出了渗透率和水力传导率的关系：

(11)

(12)

式中：ρf是流体密度,kg/m3；g为重力加速度,m/s2;μ为液体黏度系数,N·s/m2；k为固体基质渗透率;p1-p2为水头压力差。

将式(11)、式(12)带入式(10)可得：

(13)

通过渗流和存储函数计算可得岩体的渗流场方程：

(14)

在式(14)中，存储方程式为：

(15)

(16)

式中：Qm为质量源项；ε为体积应变；Ef为流体体积模量,GPa。

重力平衡方程公式为：

▽σ=ρg=(ρfφ+ρd)g

(17)

有效应力-应变关系：

(18)

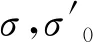
有效应力：

(19)

式中：σ0为初始有效应力,kPa；p和p0分别为孔隙水压力和初始孔隙水压力,kPa。

1.3 开挖后流体变化

在连续开挖过程中，通常原位应力发生变化并在开挖区域周围分布，这种现象会影响孔隙水流动状况的变化。特别是在发掘破坏区和开挖扰动区受开挖过程中岩体分布应力破坏的影响。

开挖后渗透率变为应变的函数，如式(20)所示：

k=kie7000εd

(20)

(21)

应变εd和固有渗透率ki与开挖后测量新渗透率有关。也就是说，开挖扰动区的新渗透率是体积应变和塑性应变的函,如式(22)所示：

kex=ki×e(200εv+350εp)

(22)

式中：kex为开挖扰动区渗透率；ki为原位渗透率；εv为开挖后岩体体积应变；εp为开挖后岩体塑性应变。

2 模型建立

2.1 工程概况

花阳隧道为重庆三环高速公路合川至长寿某标段，位于重庆市渝中区木耳镇金刚村。为双向四车道高速公路，设计速度为80 km/h，隧道宽10.25 m，高5 m，设计荷载为公路-Ⅰ级。本文研究的小净距富水段位置为K41+065—K41+14段。区段属构造侵蚀丘陵地貌区，隧道大体沿垂直构造线方向布置，与岩层走向呈大角度相交。分布地层岩性为侏罗系中统上沙溪庙组(J2s)强风化泥岩、中风化泥岩及中风化砂岩泥岩、砂岩等，分布不均匀，部分地段基岩出露[12-14]，各地层岩性特征如表1所示。节理裂隙发育，岩体破碎，涌流状出水。依据《公路隧道设计规范》(JTGD 70—2004)第3.6.3-3.6.5条规定的质量指标BQ值判断法，计算此区段围岩等级为V级。

表1 隧道下穿岩层分布

2.2 花阳隧道耦合计算模型

本文采用COMSOL Multyphysics数值模拟软件对流固耦合状态下隧道开挖过程进行模拟计算[15]。根据隧道设计，富水小净距段间距为6 m，埋深30 m，富水段长度为30 m，隧址合川端洞口附近发育陡崖，岩性主要为泥岩与砂岩不等厚互层，由于岩质软硬不同，风化差异，形成凹凸不平的陡崖断面，凸出的岩石由于陡倾节理裂隙发育，富水段位置由于崩塌、落石的物质来源比较丰富，危岩体发育，在流固耦合等不利作用下易产生崩塌，对隧道施工及运营安全有一定影响。为研究隧道开挖过程中围岩稳定性，数值模拟中富水段设置为具有孔隙水压力，模拟工况如表2所示。

表2 工况设置

根据隧道设计以及隧道地质建立隧道几何模型，如图1所示。围岩参数采用现场勘测数据并结合隧道设计规范进行选取，如表3所示。

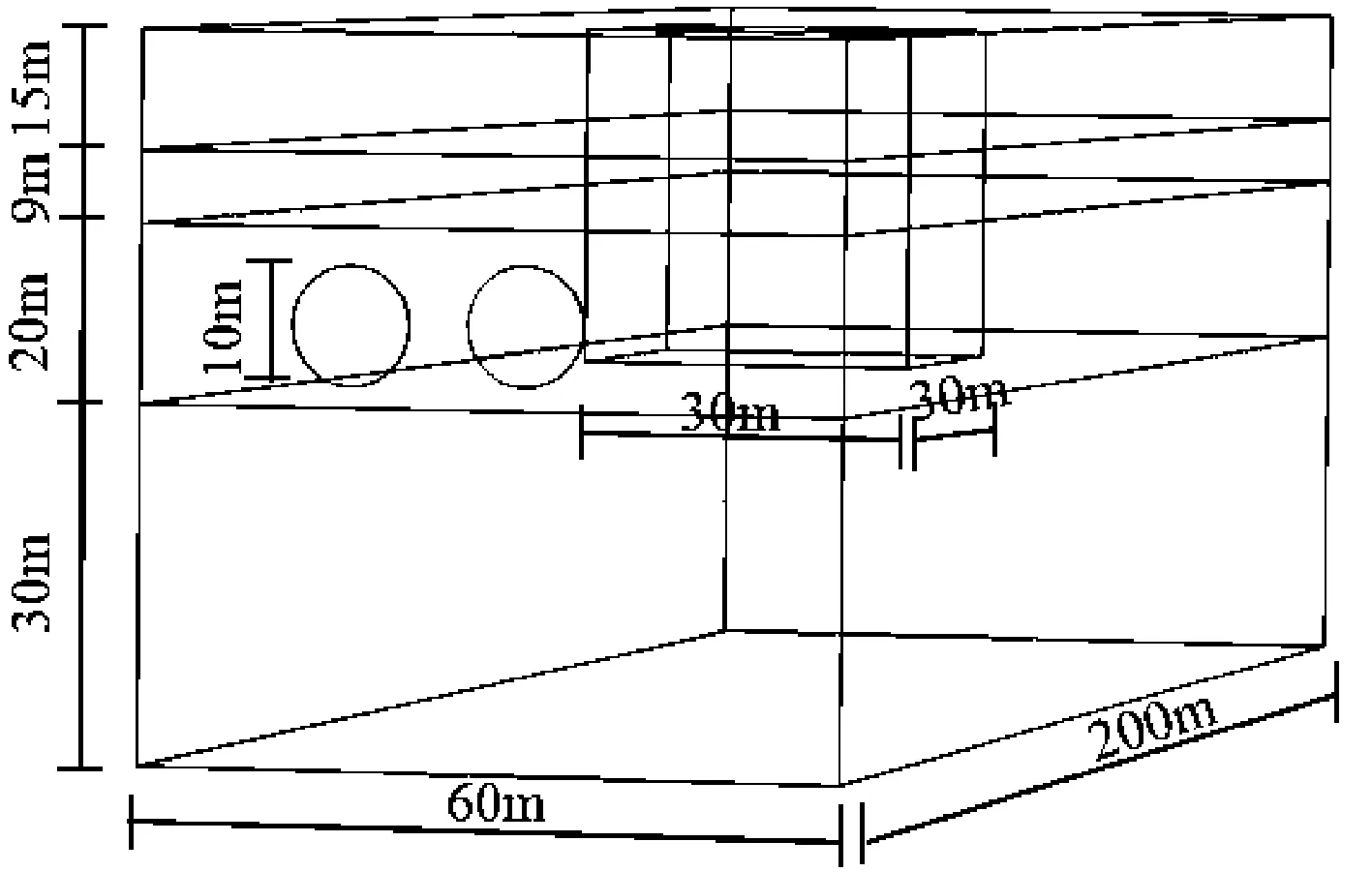
图1 模型几何图

3 计算结果分析

3.1 未开挖时地应力分布

通常，当覆盖层应力随着深度的增加而增加时， 随着开挖， 原地应力会重新分布， 应力会集中在隧道轴线周围。 应力分布的主要作用是由开挖的几何形状、岩石材料的性质和类型、 含水率、 岩石破裂和断层的存在等引起的。垂直应力分布主要由重力效应影响， 即深度的增加会增加原地应力， 但是当存在孔隙水压力时， 有效应力会在应力分布中起主要作用。

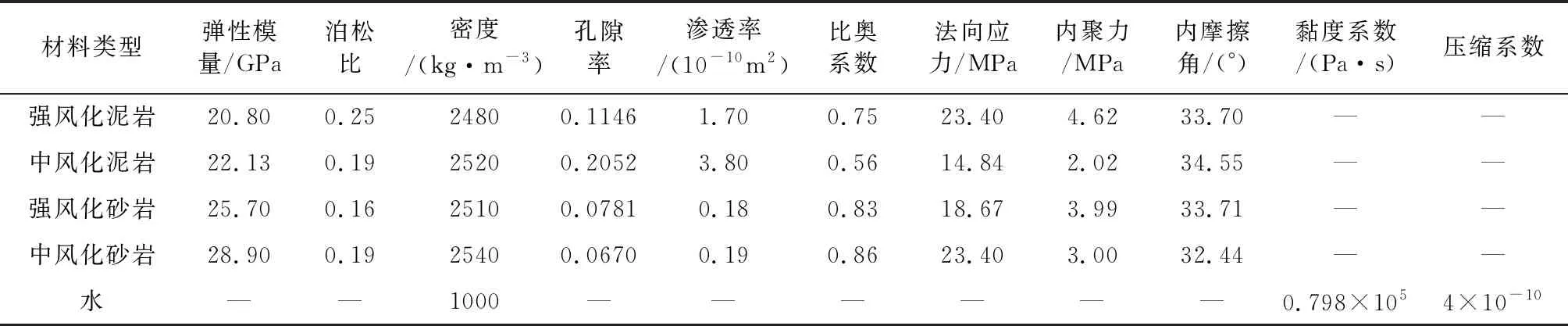
表3 模型计算物理参数

根据图2、图3可知，原位应力是指施加的重力载荷，其比重与深度相对应，并且与孔隙压力分布有直接关系。应力分布必须在开始任何研究之前仔细研究，并作为开挖稳定和安全的条件。

图2为岩体未开挖时三维垂直应力分布图，从图2可知，岩体的底部存在最大垂直应力。有水压力和无水压力对比结果可知，考虑水压力时根据公式(1)有效应力原理可知，有效应力会在应力分布中起主要作用。

图3是地应力分布的z-x断面图(y= 30 m)，由图3可知随着边岩体深度的增加，应力也以类似的方式增加。此外，在富水的截面处，在隧道轴线上的应力大于其他位置，因此，可以肯定的是，水压成为增加原位应力的附加载荷。

图2 开挖前原地应力分布

3.2 水压力对稳定性影响

为了测量由于水压变化而对稳定性产生的影响，选取工况2、工况3、工况4进行对比分析。

图3 地应力分布z-x断面图

3.2.1 开挖后垂直应力分布

垂直应力是在开挖的侧壁上测量的，因为该区域具有最大的压应力，因此选取点(110，30，-27)为研究对象，计算获得不同工况下的开挖后垂直应力分布规律。以下是不同情况下的观察图。

根据图4不同水压力下垂直应力变化可知，应力曲线在工况2、工况3、工况4下随水压的轻微变化而变化。开挖前后的变化范围几乎是恒定的，但是在距离富水段10 m的测量范围内，测量点应力的出现急剧增加，在富水段垂直应力增加了50%，开挖进一步增加时，应力曲线会波动，但在测量点后面10 m处几乎恒定。发现每条曲线的最大垂直压力约为3.3 MPa，因此可在富水段开挖会现应力突变，从而增大开挖失稳风险。

由于开挖前后的孔隙水压力增加，根据有效应力原理应力水平会略有下降。孔隙水压力越大在通过富水段时垂直应力变化越小，水压为4 MPa时模型曲线的垂直应力最小。

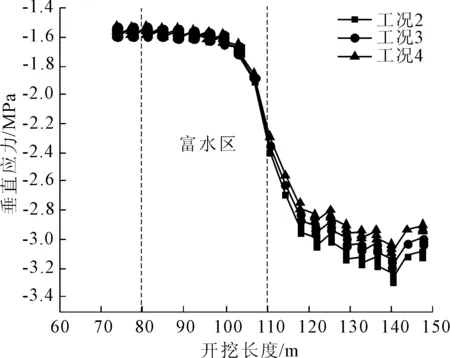
图4 开挖后不同水压力下垂直应力

3.2.2 孔隙水压力变化

根据图5开挖后不同工况下孔隙水压力分布，可以看出在不同开挖长度不同水压条件下的孔隙压力分布。曲线分布规律基本保持一致，但分布值却有所不同。水压最大的工况4的分布曲线具有最大的初始值，水压最小的工况2的分布曲线具有的最小初始值。开挖前的曲线是非线性的，并向测量点逐渐减小，与该点上的开挖平行。但从图中可以看出，水压力越大时开挖距离富水段越远越先进入突变区。水压力在4 MPa时，在距离富水段30 m时开始发生突变，而1 MPa时，在距离富水段10 m开始发生突变。

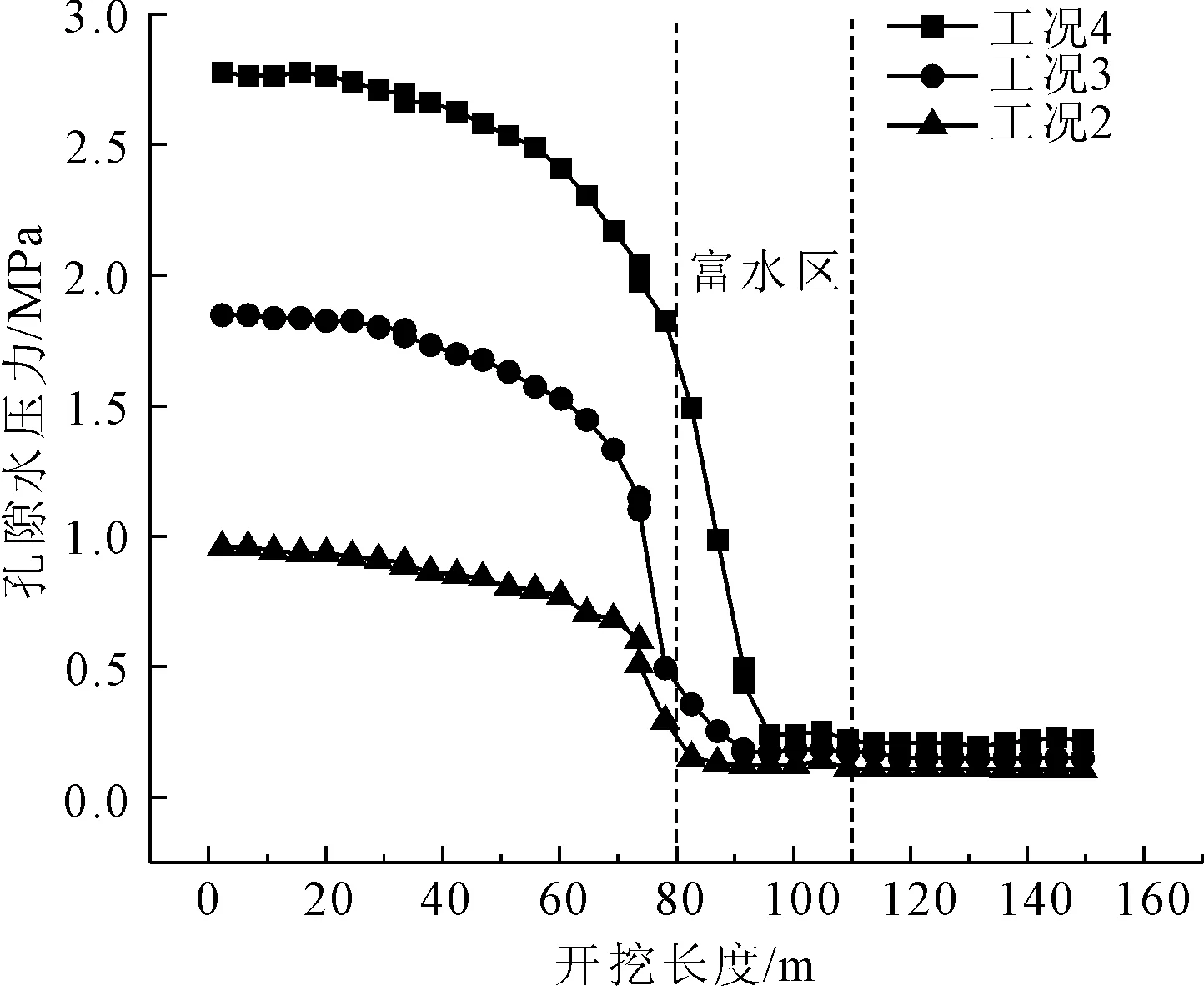
图5 开挖后不同工况下孔隙水压力分布

图6是不同开挖长度的孔隙水压力z-x断面(y=30 m)，从未开挖到开挖50 m、100 m、150 m的动态变化云图。随着隧道不断开挖孔隙水压力逐渐变小，当开挖到富水段时，可以看到孔隙水压力发生突变，由最初的4 MPa直接变到了0.1 MPa，这对于隧道开挖的整体稳定性会产生影响，需要考虑进行支护来提高工程的稳定性。

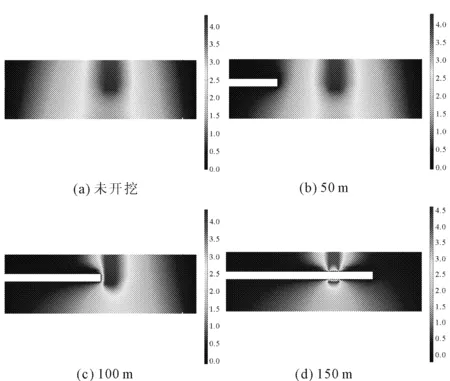
图6 开挖后孔隙水压力动态变化情况

3.2.3 位移变化

图7中给出帮部、顶部和底部的位移测量点位置，A为帮部位移测量点，B为顶部位移测量点，C为底部位移测量点。

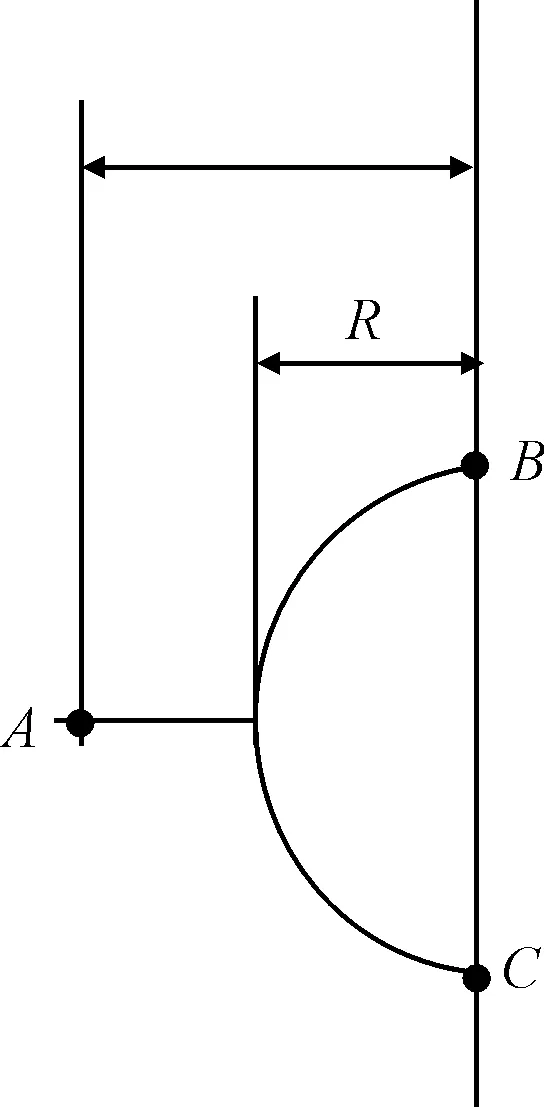
图7 位移测量点示意图

根据图8可知在不同的开挖长度中观察到由于开挖导致孔隙水压力变化而引起的应力重分布可以发现，直到在测量点之前10 m～15 m为止，开挖前的位移几乎等于零，此后位移急剧增加，经过测量点后短时间内稳定了位移，并再次继续急剧增加。开挖到距离富水区约20 m时，位移开始发生突变。随着水压力的增加最大位移呈下降趋势，1 MPa时的最大帮部位移为10 mm而4 MPa时为8 mm。

为了测量由于孔隙水压力条件变化而引起的垂直位移，从图9可看出，顶部的垂直位移远大于底部的位移。随着隧道开挖，顶部和底部的位移呈现S型曲线变化。无论是顶部还是底部在距离富水段10 m时位移发生突变，富水段出现最大位移，最大位移可达30 mm。同时在底部位移中前期开挖非富水段出现隆起。同时，发现由于孔隙水压力的变化，开挖后的变形不同于开挖前的变形， 通过比较研究发现，孔隙水压力影响较小的工况2在顶部变形最小，而在底部变形最大。

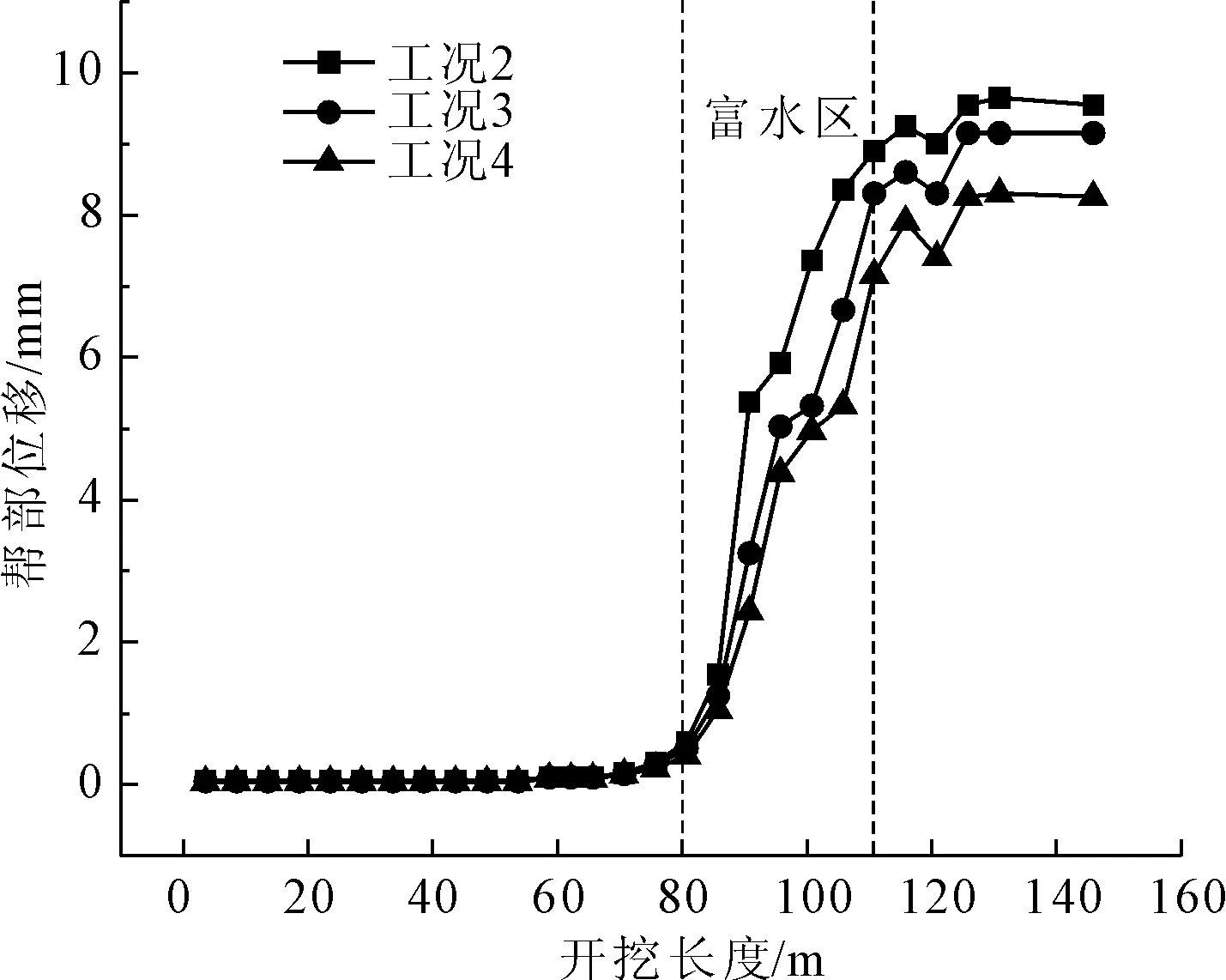
图8 开挖后帮部位移变化

图9 开挖后垂直位移变化

4 结 论

(1) 在数值模型中，建立基于弹性多孔介质和Biot-Willis模型理论的流固耦合模型。流固耦合模型通过不同的开挖距离(开挖步长)将中间迭代过程中的应力结果嵌入到流体模型中的孔隙水压力的中，实现了开挖与渗流引起的应力重分布之间的相互作用和耦合。

(2) 未开挖时，在富水的截面处，隧道轴线上的应力大于其他位置，孔隙水压力成为增加原位应力的附加载荷。

(3) 通过对富水段研究，发现开挖影响的主要范围是距离富水段开挖前10 m和开挖后30 m，在距水体10 m的范围内，应力和变形将急剧增加，突变率将近50%，在开挖富水隧道，应该在此范围内对隧道进行加固，维持隧道稳定。