基于超短期功率预测的配电网调度模型

董苏

摘   要：提出了一种基于超短期风电功率预测的滚动配电调度模型。在配电调度过程中，模型不仅可以同时修正传统机组的功率输出，还可以修正风力发电的功率。利用二阶马尔可夫（Markov）链模型对风电预测误差状态（WPPES）进行修正，并更新剩余时段的风电风力发电预测结果。该模型考虑了多时段功率平衡、机组输出调节、上旋备用和下旋备用的约束条件，并结合素数对偶仿射尺度内点法进行求解。最后的仿真验证了该方法的经济性和有效性。

关键词：滚动配电调度;超短期预测;马尔可夫链模型;素数对偶仿射尺度内点法

中图分类号：V242.3                               文獻标识码：A

文章编号：1003—6199（2020）02—0073—05

Absrtact：A rolling generation scheduling model based on ultra-short-term wind power forecasting is proposed.In the process of power generation dispatching，the model can not only revise the power output of traditional units，but also revise the power of wind farm. The second-order Markov chain model is used to modify the WPPES and update the wind power prediction results in the remaining period. The model takes into account the constraints of multi-period power balance，unit output regulation，up-spin and down-spin standby，and is solved by the primal dual affine scaling interior point method. Finally，the simulation results show that the method is economical and effective.

Key words：rolling generation scheduling;ultra-short term prediction;Markov chain model;prime dual affine scaling interior point method

随着全球能源短缺和公众对环境问题的关注，研究人员正致力于将可再生能源有效地整合到现有的配电网中[1]。风力发电作为目前技术和经济上最有发展前景的可再生能源，已逐渐成为一种主要的煤电替代形式。然而，风能具有不稳定性和不可控制性，这就导致了风力发电的不确定性和间歇性，并增加了预测的难度[2]。因此，考虑大规模风电渗透的电力系统经济和安全运行面临着巨大的挑战。文献[3]引入了条件风险法对风电综合系统进行了安全经济调度。文献[4]引入了基于随机规划的动态经济调度模型。然而，风力发电预测精度随时间推移具有降低的特点[5]，这必将严重影响日前调度的合理性，给自动发电控制（AGC）[6]提供的调度服务带来沉重的负担。

提出了一种滚动配电调度模型求解超短期风电预测信息引入经典的经济调度问题。采用二阶离散时间马尔可夫（Markov）链模型对风电预测误差状态（WPPES）进行修正，并更新剩余时段风电预测结果。该模型不仅考虑了常规机组功率输出，而且还考虑了风力发电的功率输出。最后利用素数对偶仿射尺度内点法求解该模型。

1   风电超短期预测

1.1   WPPES的Markov链转移矩阵估计

非参数离散时间Markov链模型在合成风速和风力发电时间序列的生成中已得到广泛的应用[7-9]，其仿真结果通常对生成的风力发电时间序列的概率密度函数（pdf）和自相关函数（AF）都具有很好的拟合性。

为了避免风力预测对风力发电的累积误差，采用二阶Markov链模型直接估计WPPES的转换矩阵：

其中，ΔPW（th）为时间间隔[th-1，th]内的预测误差状态。状态变量离散化可定义有限组状态值{S1，S2，…，SN}，N为修正参数，其设置可参考文献[10]。本文将最小值S1和最大值SN分别设置为-PW，n和PW，n，其中PW，n为风力发电名义功率。其余值S1，S2，…，SN设置为区间[0，1]上所定义的长度相等的N-2类的中心。在离散化有限Markov过程中，状态在任意步骤的概率只依赖于前一个状态[11]。

对于第N种状态，过渡矩阵P（th）是N×N×N矩阵。元素pkij（th）表示th+1时刻过程状态为Sj的概率，则pkij（th）的估计值为：

1.2   配电调度中的强制程序

风力发电的WPPES时间序列ΔPW（th）必须根据历史风力发电数据预先建立：

其中，第i个元素πi（th）表示ΔPW（th）在th时刻的概率。因此，公式（4）得到th时刻的状态概率向量可以转换为：

通过公式（5）和状态概率区间[π0（th-1），π0（th-2）]所定义超短期风电预测过程，th-1时刻和th-2时刻的观测状态概率向量可利用时间窗内收集的最新数据进行计算。在剩余的调度时段内，利用最大概率状态修改WPPES，进而未来的风力发电可以滚动更新。

2   滚动配电调度模型

通常日前调度可分为连续调度和等步长调度，如果一天的时间以Δt = 15 min为区间，可划分为96个时段。同时，风力发电具有快速波动，尤其是每分钟之间存在微小变化波动，这需要借助机组的惯性和控制死区进行平滑处理[12]，因此可以得出结论，并非所有的风力发电波动都会影响日前调度的合理性。为了将滚动调度和日前调度联系起来，本文以Δt = 15 min为区间更新风力发电预测值，即每15 min滚动一次机组输出功率和风力发电输出功率。

2.1   功率平衡滚动约束

在调度时段初始时刻h，系统功率平衡滚动约束为：

其中，NG为常规发电机数量;h为第h个调度时段;Ph   Gi·t为第i个常规发电机在经过h次修正后的t时刻的功率，当h = 0时，表示日前调度功率输出;Ph   W·t为经过h次修正后 时刻风力发电的功率输出，当h = 0时，表示风力发电的日前预测功率，P latestL·t     是 t时刻系统的最新功率预测。

2.2   常规发电机的成本函数

对于常规发电机，可假定二次成本函数，将调度第h时段至第96时段的总运营成本表示为：

其中，Ci为第i台常规发电机的运行成本，可表示为：

其中，ai，bi和ci为第i个常规发电机的成本系数，该系数可从发电机的投入产出曲线中得到，并取决于所使用的特定燃料类型[13]。

2.3   弃风功率计算

根据超短期风力发电预测值，剩余调度时段的弃风功率可计算为：

其中，f2（Ph   W·t）为第h时段至第96时段的弃风功率;P h*   Gi·t为t时刻风力发电超短期预测功率。

2.4   其他约束

（1）风力发电功率輸出限制为：

（2）发电机爬坡速率限制为：

其中，ΔP Gi·up和ΔP Gi·dn分别为第 台发电机的爬升速率和下降速率限制值。

（3）发电机运行功率限制为：

其中，P Gi·max和ΔP Gi·min分别为第i台发电机的最小和最大功率输出。

（4）调节偏差限制：

为了确保日前调度和滚动调度的相关性，常规发电机的最大调节偏差设置为：

其中，γi为第i台发电机允许的最大调节偏差。

（5）上下旋转备用约束：

本文系统集成了大规模风力发电，还需要额外的旋转备用容量来降低AGC对发电机的甩负荷和释放调节能力的概率：

其中，P h        usGi·t和P h        dsGi·t分别为t时刻第i台发电机的向上和向下旋转备用容量;T10为旋转备用响应时间，T10 = 10 min;Lu%和Ld%分别为系统功率预测误差向上和向下旋转备用需求系数;wu%和wd%分别为风力发电预测误差向上和向下旋转备用需求系数。

2.5   滚动配电调度模型

将惩罚因子ω纳入滚动配电调度模型中，以此协调常规发电机运行成本最小化与非弃风风力发电之间的矛盾关系，将ω设定为每组风力发电转换成常规发电机输出的等效成本，在数值实验中取max（ai γi + 2ai P Gi·max+ bi）。基于公示（6）-（17），滚动配电调度模型可以表示为：

同时，公式（18）还需要满足如下约束条件：

其中，F为剩余调度期中第 时段至第96时段的总成本，H为目标函数的二次系数矩阵，c为一次项的系数向量，x为常规发电机和风力发电的功率输出变量，h（x）为等式约束函数，g（x）为不等式约束函数，其上、下限分别为g-和g+。

3   素数对偶仿射尺度内点法

3.1   求解方法

主要问题是求解滚动配电调度模型公式（18）的凸二次规划问题中H是半正定矩阵，进而可以将其划分为一系列的对数子问题，然后利用素数对偶仿射尺度内点方法[14]沿拉格朗日双中心路径迭代进行计算。

首先，将公式（19）与公式（20）的线性约束转换为以下标准形式：

其中，A1、A2表示约束函数的系数矩阵，b1、b2表示常数项向量，e为单位列向量。通过引入松弛变量，满足如下条件：

则拉格朗日对偶问题可转化为：

其中，y、z分别为等式约束和不等式约束的拉格朗日乘子向量，I是单位矩阵，A = A1    0A2    I，b = [bT1，bT2]T。

3.2   算法步骤

步骤1：输入原始参数和上一周期计划的功率输出插补。更新剩余时段的最新预测功率需求和超短期预测风力发电。

4   实验模拟

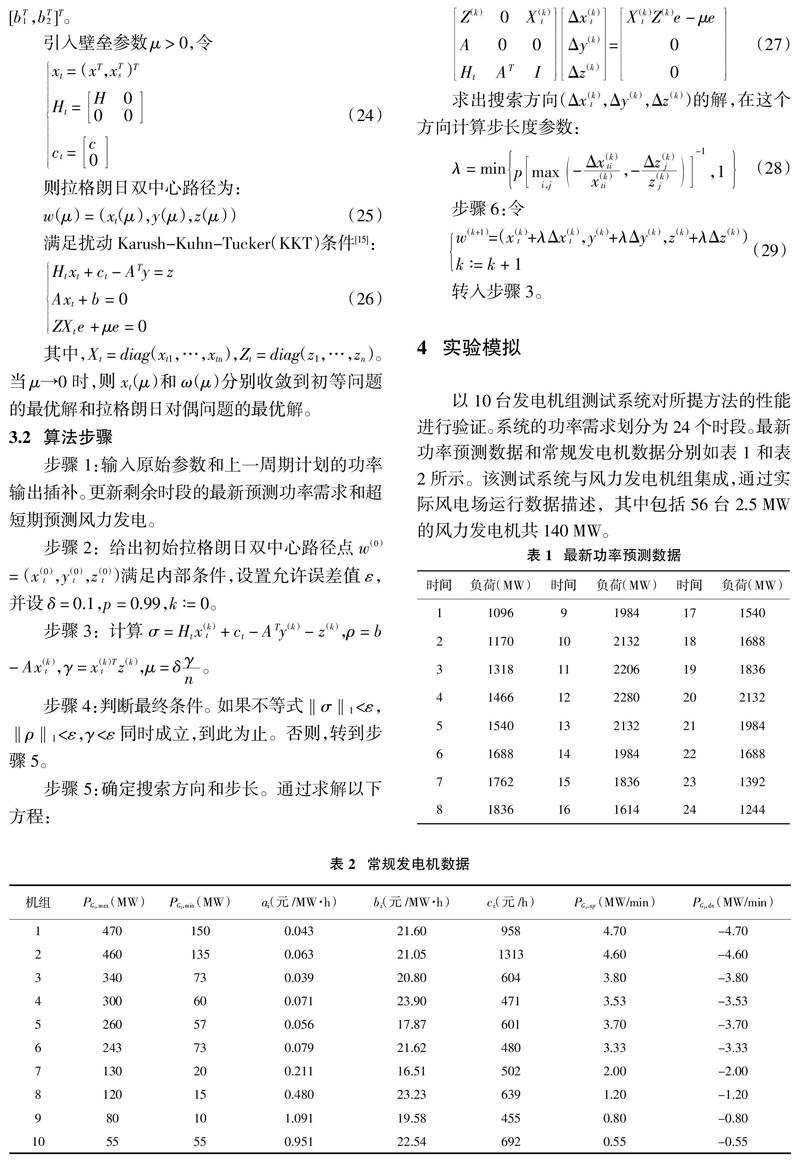
以10台发电机组测试系统对所提方法的性能进行验证。系统的功率需求划分为24个时段。最新功率预测数据和常规发电机数据分别如表1和表2所示。该测试系统与风力发电机组集成，通过实际风电场运行数据描述，其中包括56台2.5 MW的风力发电机共140 MW。

根据日前预测数据和二阶Markov链模型得到的超短期预测数据和一天实际输出数据绘制的风力发电曲线如图1所示。日前预测的趋势比超短期预测的趋势更接近实际输出的趋势。图1还表明，仅根据日前预测进行调度会产生一定的差异，这将不利于常规发电机功率输出调度的合理性，并可能造成风能资源的浪费。

由图1可知，在前30个时段执行滚动调度算法时，日前预测出现较大偏差。测试硬件环境为4 GB内存和Intel（R） Core（TM）4 Duo CPU 2.80 Ghz，并在MATLAB上进行编程。在本例中，γi = 0.1，wu% = 0.1，wd% = 0.3，Lu% = 0.05，Ld% = 0.05，

ω = 202.8，ε = 0.01。在这种情况下，计算时间仅为1.94 s，迭代次数仅为14次，可以满足在线滚动配电调度计算的需要。修正前后的目标函数值如表3所示

由表3可知，经滚动修正后，每时段的平均弃风功率降低15.237 1 MW，常规发电机运行成本节约71 192元。因此，滚动配电调度不仅可以减少弃风功率，而且可以使电力系统在节能降耗的同时容纳更多的风力发电。

5   结   论

提出了一种基于马尔可夫链模型方法的超短期风电预测滚动配电调度模型。在配电调度过程中，模型不仅可以同时校正传统机组的功率输出，还可以校正风电场的功率。仿真结果表明，该模型能有效地促进电力系统适应风力发电，优化运行成本。

参考文献

[1]    余浩斌，周江昕，衣涛，等. 考虑经济性的可再生能源并网研究[J]. 电气自动化，2018，40（05）：26-29.

[2]    曾文珺，吕丽霞. 数据挖掘技术在风力发电中的应用综述[J]. 仪器仪表用户，2019，26（04）：95-99.

[3]    刘皓玉. 间歇性风电并网能源调度综合模糊评价系统设计[J]. 计算机测量与控制，2019，27（03）：284-287.

[4]    王一飞，王秀丽，齐世雄，等. 考虑风电和负荷不确定性的灵活阻抗元件规划[J]. 电网技术，2019，43（06）：2087-2093.

[5]    陈颢天，尹超群.基于聚类算法的风力发电数据分析与预测[J]. 信息技术，2018（04）：134-140.

[6]    杜少山. 光伏并网对电网自动化控制系统的影响分析[J]. 通信电源技术，2019，36（02）：74-75.

[7]    叶永友，何承高. 海上风力发电塔脉动风速模拟研究[J]. 价值工程，2018，37（35）：151-153.

[8]    曹筱欧，王冬，周静，等. 含储能及新能源发电的居民侧需求响应[J]. 信息与控制，2017，46（03）：379-384.

[9]    靳绍珍，毛志忠，李鸿儒. 考虑不确定性因素的微电网经济运行的优化[J]. 控制理论与应用，2018，35（09）：1357-1370.

[10]  張涛，顾洁. 高比例可再生能源电力系统的马尔科夫短期负荷预测方法[J]. 电网技术，2018，42（04）：1071-1078.

[11]  王继拓，王万成，陈宏伟. 基于回归-马尔科夫链的光伏发电功率预测[J]. 电测与仪表，2019，56（01）：76-81.

[12]  袁雅琳.风力发电技术与功率控制策略[J]. 电子技术与软件工程，2018（21）：208-210.

[13]  孙鑫，陈金富，段献忠，等. 计及高维随机变量的随机响应面法概率潮流计算[J]. 中国电机工程学报，2018，38（09）：2551-2560.

[14]  田雨. 向量值约化子空间超仿射小波对偶框架的构造[J]. 吉林大学学报（理学版），2017，55（05）：1112-1116.

[15]  晏鸣宇，艾小猛，张艺镨，等. 考虑机组禁止运行区间的含风电鲁棒机组组合[J]. 中国电机工程学报，2018，38（11）：3195-3203.