基于DEM的气温空间插值方法比较

马 诺，唐 冶，常 存，贾丽红

(1.新疆气象台，新疆 乌鲁木齐 830002；2.中国气象局乌鲁木齐沙漠气象研究所，新疆 乌鲁木齐 830002；3.中国科学院新疆生态与地理研究所，新疆 乌鲁木齐 830011)

引 言

气温是主要的气象要素之一，具有重要的地理学和生态学意义，但受客观因素限制，气象观测站的数量有限且分布不均[1]。现有的观测站气温数据无法满足地学模型、气候模型、水文模型等相关研究的空间精度要求，因此无站区域的气温数据只能通过间接推算获取，目前常用的推算方法包括客观分析法、资料同化法、遥感反演法及空间统计插值法，其中，空间统计插值法是利用有限的气象观测站气温数据插值模拟未知点的气温数据，是离散站点气温网格化的重要手段之一[2-3]。

传统的气温插值方法是将站点视为同一平面上分布的离散点，其忽略了数据的空间分布特征和地形高度等影响因素，因此即使采用不同插值方法，也较难获得高精度的估算结果[4-5]。20世纪90年代以来，结合地形因子的气温空间插值研究在国外得到空前发展，基于温度与经度、纬度和海拔高度相关性的各类新插值方法，构建了一系列较为权威的气温空间化数据集[6-9]。2000年后，随着GIS技术在国内的发展，DEM地形数据的充分利用也为气温空间模拟精度的提高提供了新的思路。众多研究表明，基于DEM的不同空间插值方法与传统插值方法相比，气温估算精度均有明显改善[10-12]。目前，北京市气象台将基于DEM数据、采用克里金插值法得到的高分辨率预报产品运用到了实时业务中[13]。以往研究大多是用一种基于DEM的插值方法与其他未考虑地形因子的传统插值方法进行比较，而针对基于DEM数据的不同空间插值方法间的比较研究相对较少。在新疆地区，仲嘉亮[14]采用基于DEM的“回归方程计算和空间残差”方法对气温进行插值，但未与其他方法进行比较；王智等[15]对不同插值方法进行了对比，但区内气象站点仅选用了53个，站点分布较稀疏；张连成等[16]虽然弥补了以上研究方法的不足，但仅选用了一年数据，且只是两种方法间的比较。同时，以往研究主要是对整个区域进行插值分析，而根据研究区气候差异进行分区插值的对比研究较少[17-18]。

李新等[19]分析指出没有绝对最优的空间内插方法，必须对研究区域的数据进行空间探索分析，选择最优方法。因此，对某地区的气象要素进行空间插值研究时选择适合的插值方法，并对插值结果进行精度检验非常必要。本文根据新疆2007—2016年的气温数据，在以往研究基础上选择3种基于DEM地形辅助信息的气温空间插值方法，结合境内“三山夹两盆”的特殊地形及气温分布特征，按不同气候区做进一步对比，以期选出更适合各气候区的方法为开展相关研究提供参考。

1 研究区概况

新疆(73°40′E—96°18′E、34°25′N—48°10′N)位于中国西北部，欧亚大陆中部，总面积166.49×104km2，占全国陆地总面积的1/6。国内与西藏、青海、甘肃等省区相邻，周边依次与蒙古、俄罗斯、哈萨克斯坦、吉尔吉斯斯坦、塔吉克斯坦、阿富汗、巴基斯坦、印度8个国家接壤；陆地国界线超过5700 km，约占全国陆地国界线的1/4，是中国面积最大、交界邻国最多、陆地国界线最长的省级行政区；也是中国大陆进入中亚地区最便捷的通道。

新疆北部有阿勒泰山，南部有昆仑山，中部横亘全境的天山山脉将新疆分为南北两部。天山以南有塔里木盆地，天山以北有准噶尔盆地，山脉与盆地相间排列，盆地被高山环抱，构成“三山夹两盆” 的独特地形。由于天山的屏障，使天山南北每个纬距的温差达7.9 ℃，南、北气候差异显著[20]。

2 资 料

研究所用的基础数据来源于新疆气象局，为全疆105个气象观测站2007—2016年的月平均气温、年平均气温及站点的经度、纬度和海拔高度。依据新疆独特的地貌特征及纬度地带性，将新疆划分为天山以北和天山以南两个气候区，其中，天山以北共有气象观测站53个，天山以南52个(图1)。

数字高程模型(digital elevation model， DEM)数据分辨率为30 m×30 m，采用Lambert投影，WGS-84大地坐标系；两条标准纬线分别为36.5°N和48.0°N，中央经线为32°E；椭球体为克拉索夫斯基(Krasovsky)。

3 方 法

3.1 精度检验

采用交叉验证法分别对3种空间插值方法在天山以北、天山以南区域的效果进行评估。选取天山以北42个站点作为样本点用于气温插值模型构建，11个站点作为检验点用于模型精度检验；选取天山以南41个站点作为样本点用于气温插值模型构建，11个站点作为检验点用于模型精度检验(天山以北及以南的样本点和检验点分别约占观测站总数的80%和20%)。由于新疆地区气象站点分布稀疏，所以选择检验点在尽量满足分布均匀的同时，也要确保个别站点极其稀少的边界区域内的样本点数量，以免对插值范围及精度造成严重影响。采用平均绝对误差(MAE)和均方根误差(RMSE)作为检验不同插值方法精度的标准，表现为误差值越小精度越高。

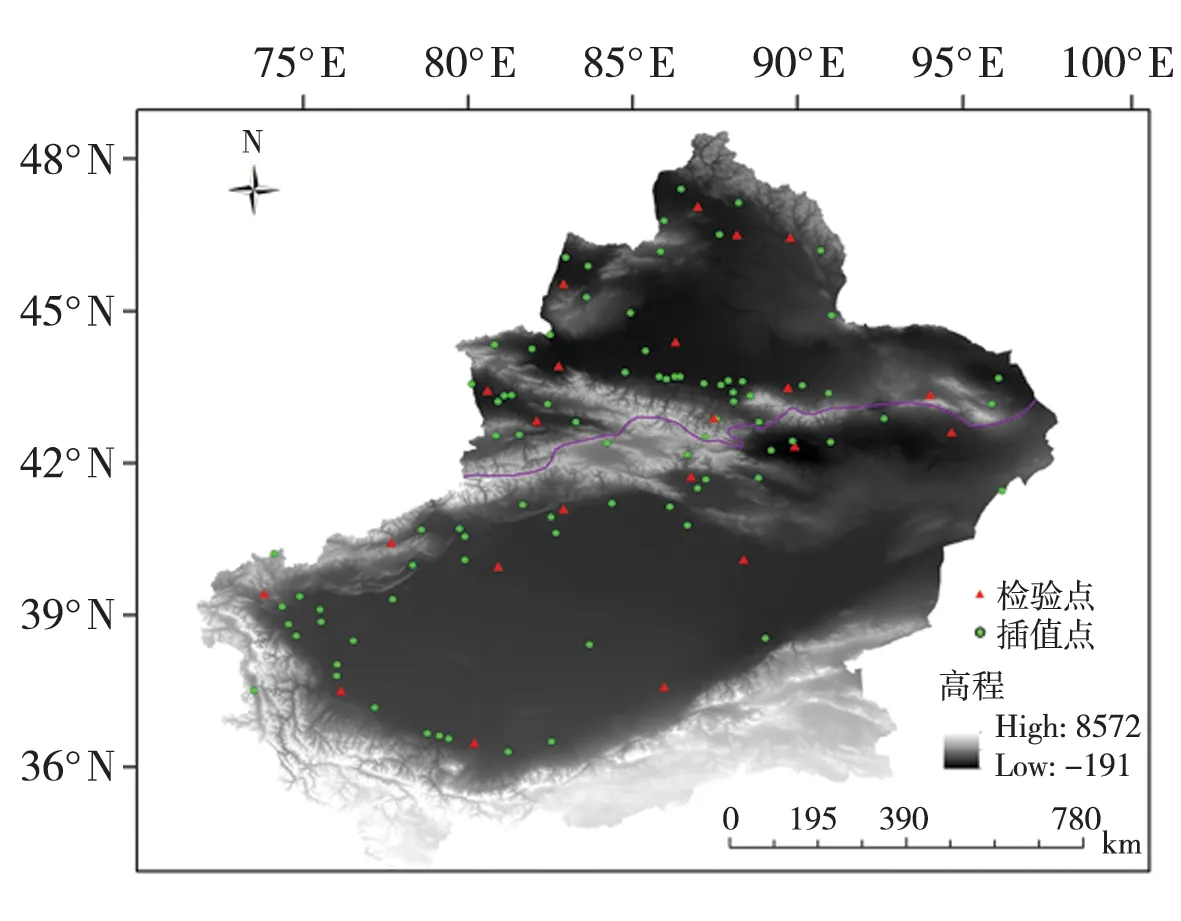
图1 新疆气象观测站点空间分布(阴影为高程)Fig.1 The spatial distribution of meteorological observation stations in Xinjiang(the shaded for elevation)

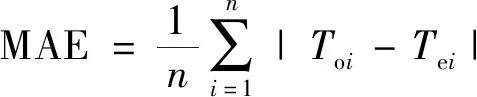
(1)

(2)

式中：n为检验站点数；Toi和Tei分别表示第i个站点的实际观测值和预测值。

另外，采用pearson相关系数来反映检验站点观测值与不同空间插值方法的预测值之间的相关程度。

3.2 基于DEM的气温订正

对流层内气温垂直递减率A为0.0065 ℃· m-1，即海拔高度每上升1000 m，平均气温下降6.5 ℃[10]。先将不同海拔高度的样本点气温值订正为海平面气温；再对海平面气温进行普通克里金插值；最后将插值得到的气温场数据与DEM数据进行栅格运算，生成具有地形特征的气温场模拟数据。公式如下：

T2=T1+AH1

(3)

T4=T3-AH2

(4)

式中：H1为样本点海拔高度；T1为样本点真实海拔高度气温；T2为样本点海平面气温；T3为插值后的海平面气温；H2为DEM高程数据；T4为还原后的真实海拔高度气温。

3.3 普通克里金插值(O-Kriging)方法

O-Kriging法来源于地统计学，是最普遍和应用最广的克里金插值方法[12]。插值过程相当于在未知的区域化变量的期望值上对样本点进行加权滑动求取平均值的过程[21]。其优点是以空间统计学为理论基础，不仅考虑了样本点的空间相关性，而且在计算待插值点估计值时，还能给出估计精度的方差，适用于较为宏观性的研究且插值效果不会产生“牛眼”效应[2,11]；缺点主要包括变异函数的确立难度大，站点数量和空间分布必须满足平稳假设前提[22]。本文中的O-Kriging方法是对订正到海平面的气温数据进行插值。

3.4 协同克里金插值(Co-Kriging)方法

Co-Kriging法是在O-Kriging法的基础上把区域化变量的最佳估算方法从单一属性发展到两个或两个以上的协同区域化属性，在计算中要用到多个属性各自的半方差函数和交叉半方差函数，比较复杂[21]。但因为Co-Kriging方法不只是对各变量做自相关预测，还包括对主变量和协同变量之间交叉相关性的估计，所以也能够更有效地改进估算精度[23]。本文中Co-Kriging方法以气温数据为主变量，DEM数据为协同变量。

3.5 多元线性回归插值法(MLR)

气温的水平和垂直地带性分布特征对气温插值结果会产生很大影响[5]。影响气温空间分布的主要因素包括经度、纬度、坡度、坡向、海拔高度、下垫面等[24]。多元线性回归插值法的优点在于以剔除多重共线为前提可增加较多自变量因子，而计算量却增加较少，在因子相关性较强的情况下可得到精度较高的模拟结果[2,12]；缺点在于该方法属于非精确插值，在地理条件复杂的观测点处存在剩余残差[25]。

将天山以北和天山以南样本点的月平均气温、年平均气温分别与通过DEM提取出对应站点的经度、纬度、坡度、坡向、海拔高度进行相关分析。表1列出天山以北和天山以南平均气温与各地形要素的相关系数。可以看出，天山以北，平均气温与坡度、高度在3—11月均表现为显著负相关，相关系数分别为-0.62～-0.40和-0.96～-0.61；与经度在11月至次年3月显著相关，相关系数为-0.54～-0.38；与纬度在12月至次年3月相关性较显著，相关系数为-0.47～-0.31；而与坡向的相关性较差。天山以南，平均气温与海拔高度全年显著负相关，其中6月相关性最好，相关系数为-0.93；与经度相关性仅在1月和7月显著；与纬度在11月至次年3月相关性最好，相关系数为-0.57～-0.36；与坡度和坡向相关性差。综上所述，平均气温与单一地形要素相关性并不稳定，且随季节变化差异较大。而无论天山以南还是天山以北，平均气温与多因子构成的复相关系数全年均呈显著正相关，其中天山以北的复相关系数为0.54～0.96，天山以南的复相关系数为0.82～0.97，明显好于平均气温与单一因子的相关性。

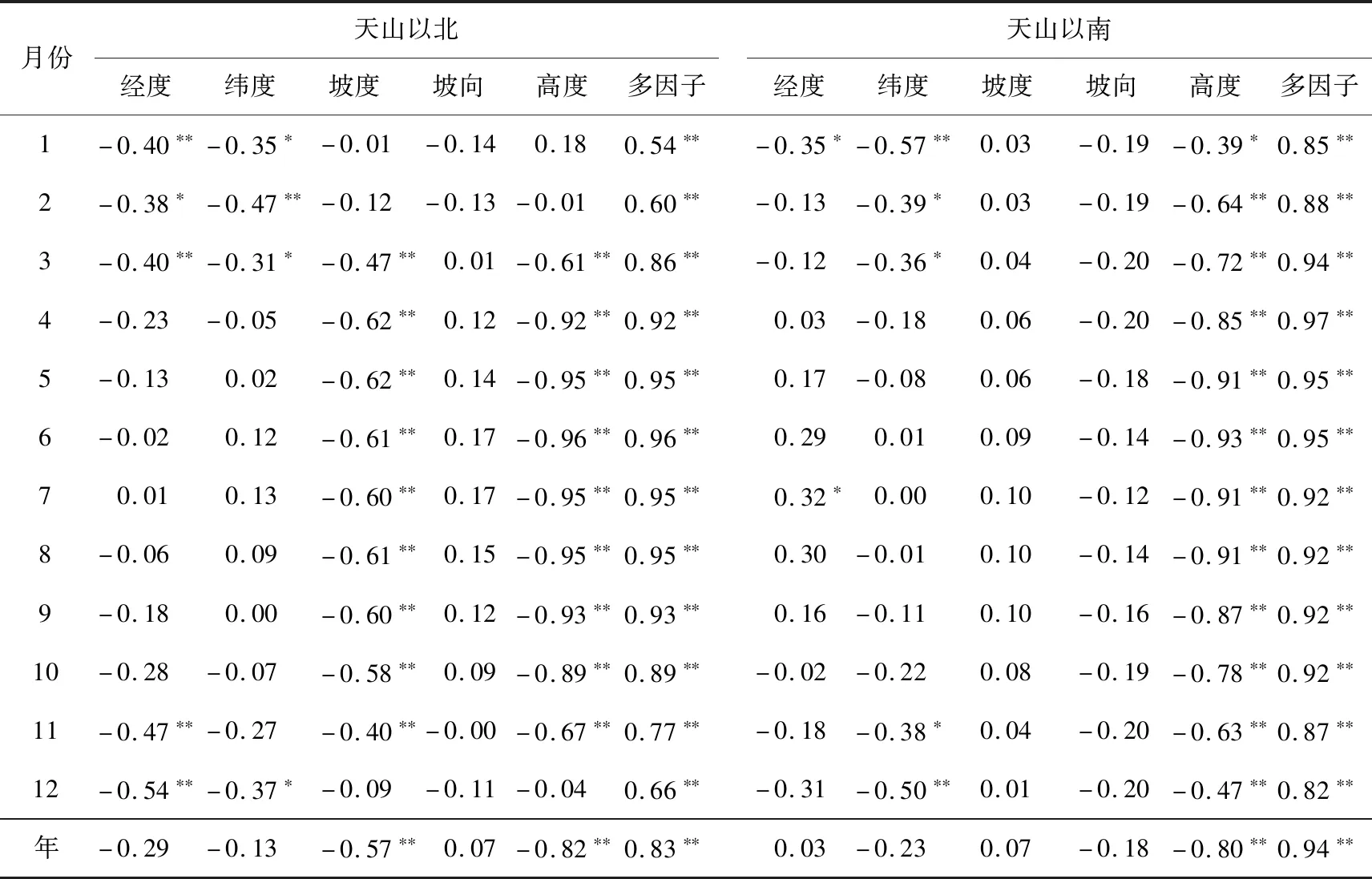
表1 天山以北和天山以南平均气温与各地形要素的相关系数Tab.1 The correlation coefficients between mean temperature and geographic elements in the north and south regions of the Tianshan Moutains

注：*和**分别表示通过0.05和0.01显著性检验，下同。

基于上述分析，经度、纬度、坡度、坡向、海拔高度等地形要素的有效组合才能更好地反映不同时段的平均气温及其变化。因此，基于DEM的多元线性回归插值模型可表示为：

T=aX+bY+cS+dA+eH+Z

(5)

式中：T为气温；X、Y、S、A和H分别为经度、纬度、坡度、坡向和海拔高度，a、b、c、d和e分别为相应回归系数；Z为常数项。表2 列出天山以北和天山以南多元线性回归插值模型。

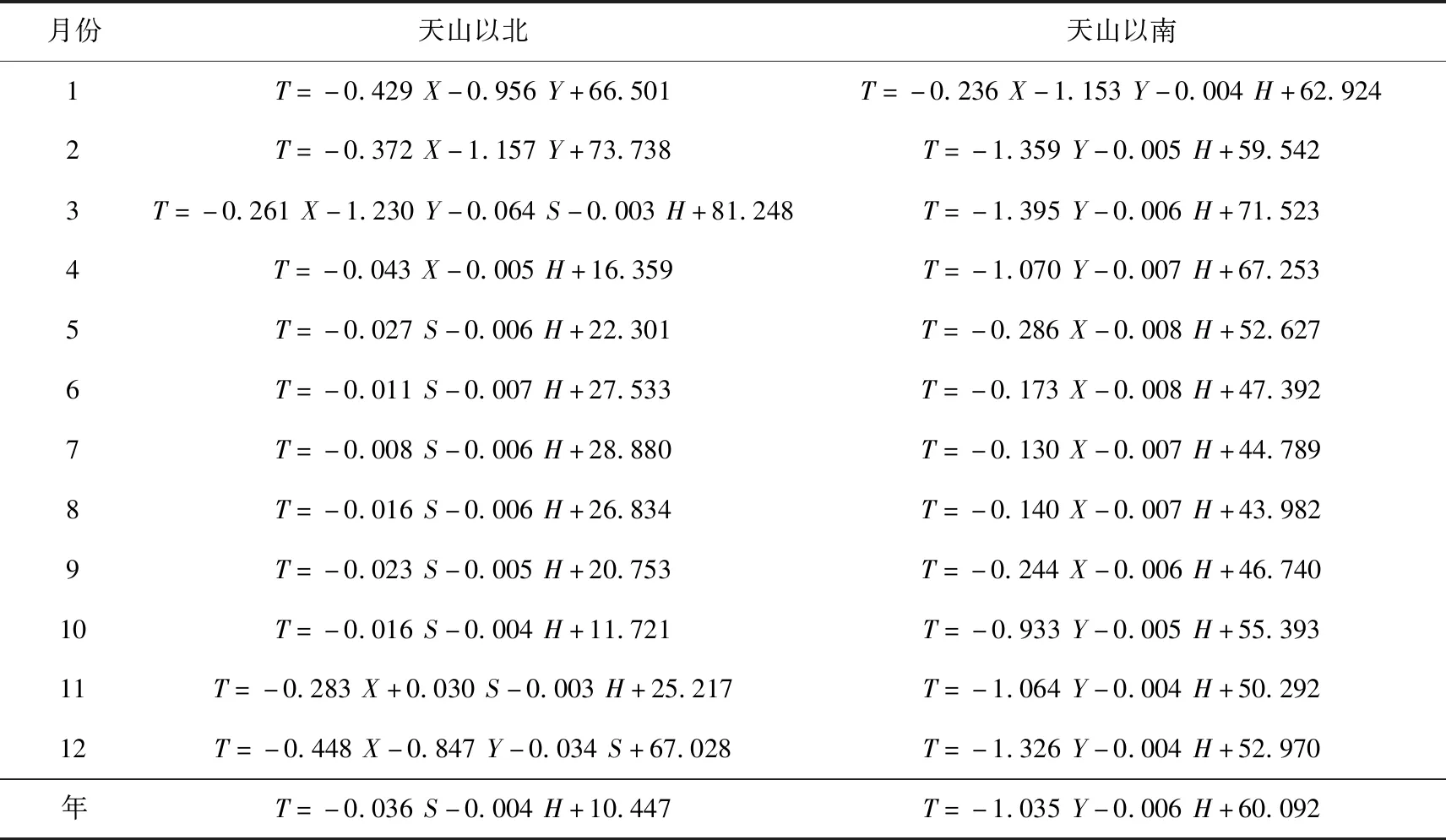
表2 天山以北和天山以南多元线性回归插值模型Tab.2 The multiple linear regression interpolation models in the north and south regions of the Tianshan Moutains

4 结果分析

4.1 不同插值方法的误差比较

图2为天山以北和天山以南3种插值方法平均气温的MAE和RMSE变化。可以看出，天山以北，Co-Kriging方法整体精度最高，MAE为0.5～1.2 ℃，平均为0.9 ℃，RMSE为0.7～1.7 ℃，平均为1.2 ℃；其次是O-Kriging方法，MAE为0.4～3.8 ℃，平均为1.2 ℃，RMSE为0.5～4.8℃，平均为1.6 ℃；MLR方法精度最低，MAE为1.0～2.3 ℃，平均为1.4 ℃；RMSE为1.3～2.6 ℃，平均为1.7 ℃。Co-Kriging方法的MAE、RMSE在3种方法中浮动最小，年均值最小，且在10月至次年3月在3种方法中值最低，分别为0.5～1.0 ℃、0.7～1.2 ℃；4—9月则以O-Kriging方法最优，MAE为0.4～0.8 ℃，RMSE为0.5～0.9 ℃。MLR方法的插值精度在1—2月虽好于O-Kriging方法，但远低于Co-Kriging法，其他时段的MAE和RMSE值分别为1.0～1.6 ℃和1.3～2.0 ℃，大于Co-Kriging或O-Kriging方法。

天山以南，O-Kriging方法整体精度较高，MAE为0.5～1.6 ℃，平均为0.9 ℃；RMSE为0.6～2.0 ℃，平均为1.1 ℃；其次是Co-Kriging方法，MAE为0.7～1.1 ℃，平均为0.9 ℃；RMSE为0.8～1.5 ℃，平均为1.2 ℃；MLR方法精度最低，MAE为1.0～1.6 ℃，平均为1.2 ℃；RMSE为1.2～2.1 ℃，平均为1.4 ℃。Co-Kriging方法的插值精度在10月至次年2月明显优于O-Kriging和MLR方法，MAE和RMSE分别为0.7～0.9 ℃和0.8～1.1℃；3—9月以O-Kriging方法最优，MAE为0.5～0.8 ℃，RMSE为0.6～1.2 ℃；Co-Kriging与O-Kriging方法对年平均气温的插值精度相同，MAE和RMSE分别为0.8 ℃和1.1 ℃；MLR方法的MAE除在1月低于O-Kriging方法，4月与Co-Kriging方法相同，其他时间均高于Co-Kriging及O-Kriging方法。

4.2 不同插值方法气温的预测值与观测值相关性

表3列出基于3种插值方法的天山以北和天山以南气温的预测值与观测值的相关系数。可以看出，天山以北，3种插值方法中，O-Kriging方法在3—12月显著相关，相关系数为0.842～0.986，4—10月相关性远高于Co-Kriging和MLR方法，且O-Kriging方法年平均气温的实测值与预测值的相关性在3种方法中最优；Co-Kriging方法与MLR方法均在全年呈显著相关，其中Co-Kriging方法的相关系数为0.864～0.976，11月至次年3月的相关性明显高于另外两种方法；MLR方法的相关系数为0.709～0.941，年平均气温的实测值与预测值的相关系数仅为0.626。天山以南，3种插值方法均表现为全年显著相关，其中O-Kriging方法在2—9月相关性最高，相关系数为0.885～0.992；Co-Kriging方法10月至次年1月相关系数为0.876～0.907，高于O-Kriging和MLR方法；MLR方法的相关系数为0.620～0.970， MLR方法年平均气温的实测值与预测值的相关性在3种方法中最优，相关系数为0.958。

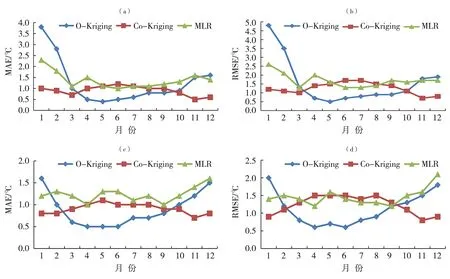
图2 天山以北(a、b)和天山以南(c、d)3种插值方法平均气温的MAE(a、c)和RMSE(b、d)月际变化Fig.2 The monthly variation of MAE (a, c) and RMSE (b, d) of mean temperature obtained based on three interpolation methods in the north (a, b) and south (c, d) regions of the Tianshan Moutains

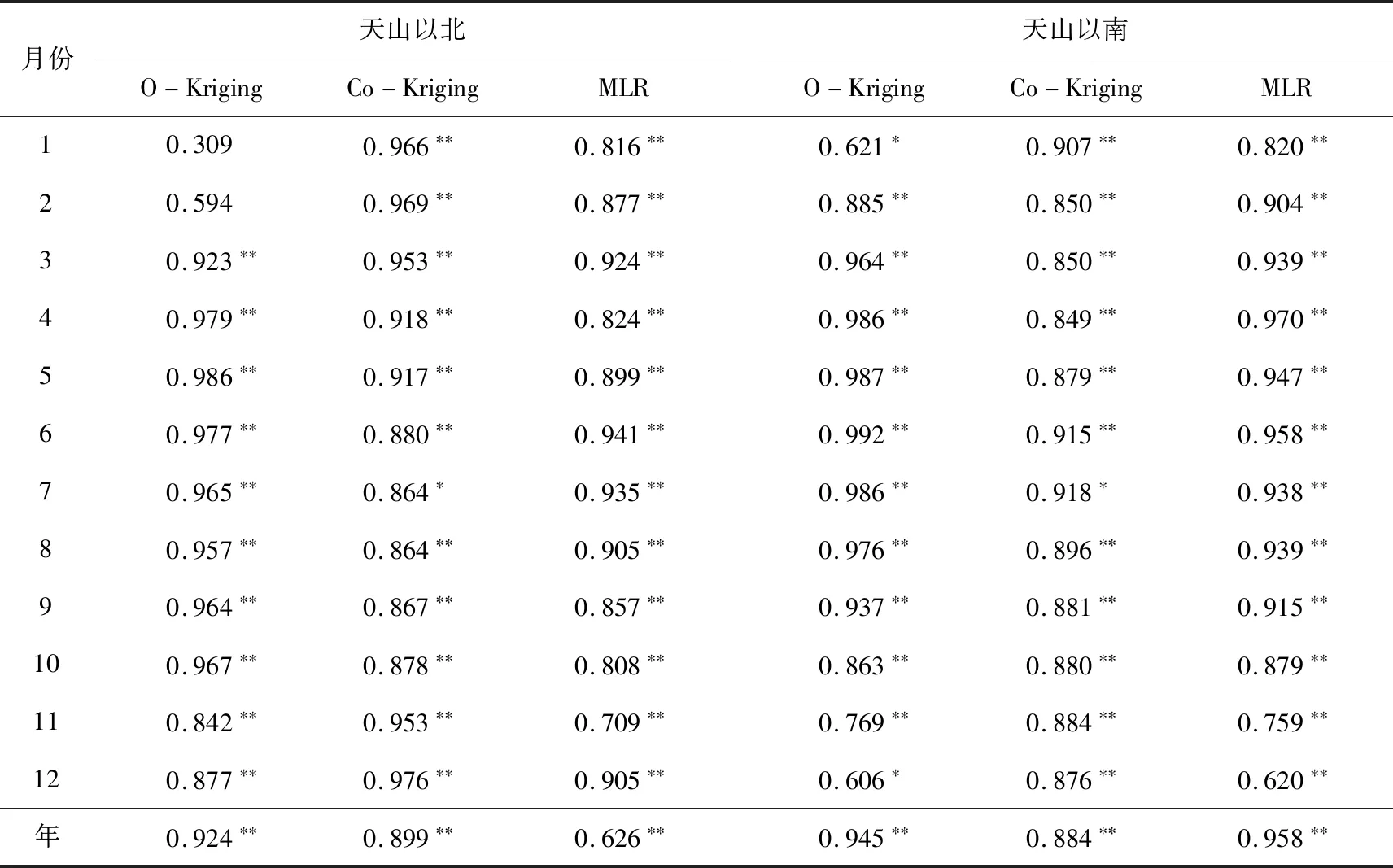
表3 基于3种插值方法的天山以北和天山以南气温的预测值与观测值的相关系数Tab.3 The correlation coefficients between the observed temperature and predicted temperature based on three interpolation methods in the north and south regions of the Tianshan Moutains

5 结 论

(1)天山以北， O-Kriging方法在4—9月表现最优，平均气温的MAE和RMSE分别为0.4～0.8 ℃和0.5～0.9 ℃；10月至次年3月Co-Kriging方法最优，MAE和RMSE分别为0.5～1.0 ℃和0.7～1.2 ℃；MLR方法插值精度最低，MAE和RMSE分别为1.0～2.3 ℃和1.3～2.6 ℃。天山以南，3—9月以O-Kriging方法最优，MAE和RMSE分别为0.5～0.8 ℃和0.6～1.2 ℃；10月至次年2月Co-Kriging方法最优，MAE和RMSE分别为0.7～0.9 ℃和0.8～1.1 ℃；MLR方法插值精度最低，MAE和RMSE分别为1.0～1.6 ℃和1.2～2.1 ℃。由于天山以北1月和2月气温明显低于天山以南，3月平均气温才到0 ℃，而天山以南3月平均气温已接近10 ℃，因此，天山以北O-Kriging方法的MAE和RMSE值在1月和2月明显高于天山以南，且从4月起其插值精度才优于Co-Kriging方法，而天山以南自3月起以O-Kriging方法为最优。

(2)基于3种插值方法的天山以北和天山以南气温的预测值与观测值的相关系数表现为天山以北， O-Kriging方法在4—10月相关性最高，相关系数为0.957～0.986；Co-Kriging方法在11月至次年3月的相关性最高，相关系数为0.953～0.976；MLR方法全年虽显著相关，但最大相关系数仅为0.941。天山以南，O-Kriging方法在2—9月相关性最高，相关系数为0.885～0.992；Co-Kriging方法在10月至次年1月相关性最高，相关系数为0.876～0.907；MLR方法的相关系数为0.620～0.970，全年波动较大。进一步对比发现，在天山以北通过O-Kriging和Co-Kriging方法得到的预测值与观测值的相关性优于天山以南，MLR方法的相关性则表现为天山以南优于天山以北。

(3)天山以北、天山以南夏季用O-Kriging方法做气温插值精度较高，而冬季Co-Kriging方法则比较适用。