钢管混凝土柱恢复力模型研究
朱铭
(江西交通职业技术学院)
0 引言
钢管混凝土构件是一种新型的组合结构,广泛应用于房建和大跨度拱桥中[1]。但由于近年来,我国地震频发,限制了钢管混凝土在地震区的应用。故研究钢管混凝土构件在地震作用下的动力响应问题迫在眉睫。
在地震作用下,结构会形成大量的恢复力与变形的关系曲线。如果直接将恢复力曲线用于动力非线性时程分析中,计算过程将十分复杂,故需要将恢复力曲线简化成恢复力模型来应用。目前,恢复力模型大多是建立在拟静力试验的基础上,根据试验所得滞回曲线来总结规律,按一定条件加以简化,最终建立构件的恢复力模型。
本文介绍了目前国内外常见的恢复力模型,并根据文献[2]中的实测荷载-位移曲线,提出了包含骨架曲线模型、滞回规则、刚度退化的钢管混凝土柱恢复力模型。
1 恢复力模型分类
目前有两大类恢复力模型:曲线型模型和折线型模型。曲线形模型是由连续的曲线构成,能很好地表达刚度变化,但是计算方法很复杂,导致其很少应用于实际工程的弹塑性分析。折线型模型则是由折线段构成,模型中存在突变点,不连续,但是计算简单,故应用广泛[3]。折线型恢复力模型有双线型、三线型、四线型、退化双线型、退化三线型和指向原点型等[4],适合于不同限制条件下的构件。
1.1 双线型
双线型模型的形式简单,计算方便,并且考虑了钢材的包辛格效应,可作为钢筋混凝土构件的弹塑性分析的基础。但它只有弹性段和强化段,未考虑刚度退化,在结构设计中是偏不安全的。
1.2 三线型
与双线型相比,三线型考虑了刚度退化的影响,有弹性段、强化段和下降段,可以较好地反映钢筋混凝土构件的恢复力特性。
1.3 四线型
四线型模型是在三线型的基础上,引入了构件的开裂点,将开裂点、屈服点、峰值点、极限点作为骨架曲线模型的特征点,更加符合钢筋混凝土构件带裂缝工作的特性。
2 恢复力模型建立
本文采用试验拟合法来建立恢复力模型,现做以下假设:①屈服点与最大弹性荷载点重合;②弹性阶段,加载和卸载刚度为构件初始刚度,屈服点后,刚度随位移增加而退化;③模型中存在软化点。
2.1 骨架曲线模型
根据文献[2]的试验结果,计算两根圆钢管混凝土柱的骨架曲线特征点,为了消除不同钢管柱参数的影响,采用无量纲的形式,最终计算结果见表1。
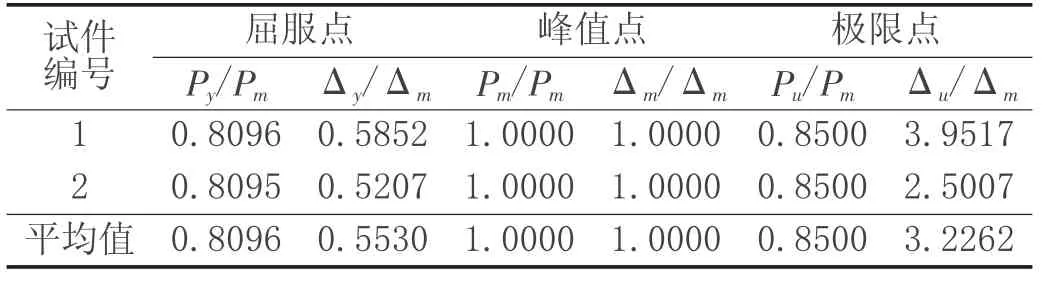
表1 骨架曲线特征点无量纲值
依据表1 中的各特征点的无量纲坐标,得到骨架曲线的三线型模型,如图1。各阶段方程为:弹性段OA:P/Pm=1.464Δ/Δm,强化段AB:P/Pm=0.426Δ/Δm+0.574,下降段BC:P/Pm=-0.067Δ/Δm+1.067。

图1 三线型模型
2.2 刚度退化
随着循环次数的增大,当加载超过屈服点后,构件不会再以弹性刚度进行卸载,而是有一定的退化。本文按照文献[5]中的割线刚度来定义构件的刚度。经过对两根钢管混凝土柱的刚度进行回归分析,得到刚度退化的规律如下:

回归分析过程见图2。其中,横坐标为位移循环等级Δi/Δy,纵坐标为各级位移循环的刚度与破坏时的刚度比值Ki/Ku。

图2 刚度退化回归曲线
2.3 滞回规则描述
总结实测滞回曲线的规律,再结合骨架曲线模型和刚度退化规律,建立适合钢管混凝土柱的恢复力模型,如图3。
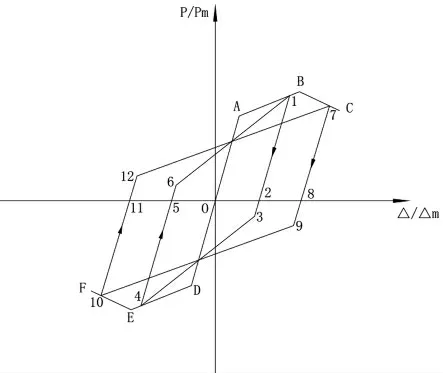
图3 恢复力模型
⑴模型采用无量纲坐标,结合骨架曲线的特征点和各级滞回环建立,图中A(D)为屈服点,B(E)为峰值点,C(F)为极限点。
⑵在弹性阶段,加载曲线沿骨架模型OA 进行,当在OA 段卸载时,沿着原路线返回原点。
⑶构件屈服后,随着循环次数的增加,卸载刚度降低。当在1 点开始卸载时,先卸载至2 点,接着反向加载至3 点,此时由于模型软化点的存在,导致在3 点处刚度发生突变,指向4 点。反向卸载至5 点,接着正向加载至6 点,6 点坐标与3 点坐标关于原点对称,最后回到1点,指向下一个滞回环。软化点的坐标可参考文献[6],取相应位移循环的峰值承载力的0.2 倍。
2.4 恢复力模型与试验值的比较
将模型和试验曲线进行比较,如图4 所示。由图可知,二者吻合良好,说明本文建立的恢复力模型能较好地反映钢管混凝土柱的滞回性能。
3 结论
⑴本文在国内外现有的恢复力模型的基础上,结合试验滞回曲线,提出了适合钢管混凝土柱的恢复力模型,并且与拟静力试验得到的滞回曲线对比。通过模型建立的恢复力曲线与试验曲线比较相符,证明推导的恢复力模型是合理的。
⑵由于参考的试验滞回曲线较少,未能充分反映影响钢管混凝土柱滞回性能的各因素,故还需更加深入、全面的研究,方能得到更加实用的恢复力模型。

图4 恢复力模型曲线与试验曲线对比

