基于激光制导的高速拦截制导精度分析
陈恩华,易文俊,刘 刚,王康健
(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)
精确制导武器有着精度高、杀伤力强等优点,在武器装备领域中受到越来越多的关注。其中,激光制导武器的制导精度尤为突出,激光末端制导弹药的圆概率误差(CEP)小于1 m,具有极高的精度。国际多款制导弹药均采用激光制导体制,如美国的“铜斑蛇”制导炮弹、俄罗斯的“红土地”制导炮弹等。而采用GPS制导方式武器的CEP一般只能达到10 m[1],随着各类导弹突防性能的不断提高,防空反导拦截也面临着巨大的挑战,来袭的导弹速度变得越来越快,防空导弹自身性能的提高也迫在眉睫。研究激光导引头的性能在高速拦截背景下对制导精度的影响具有一定的实际意义。
传统的制导精度评估方法常采用蒙特卡洛打靶的方式进行,将引起脱靶的各种不确定因素考虑进打靶过程中,通过大量的仿真进一步得到制导精度分析结果[2]。另一种制导精度的分析方法是采用伴随系统的方法,该方法没有大量的仿真试验过程,且通过一次仿真便可以得到不同末制导时间下的脱靶量,在导弹制导回路的初步性能判定及制导精度的相关分析中被大量应用[3]。
钟凌伟[4]将末制导过程中的弹-目相对运动进行线性化。根据该弹-目相对运动进行线性化模型仿真,得到了由目标机动所引起的制导精度随末制导时间的变化曲线。得出伴随法没有大量的仿真试验过程,适用于导弹制导回路的初步性能判定及制导精度相关分析的结论。杨鹏锐等[5]指出在设计初期,系统的各个模块尚不明确,无法经过蒙特卡洛方法准确地进行大量的仿真实验。通过构建原始系统及其伴随系统的方法,不仅避免了大量的仿真试验过程,同时也解决了设计初期系统的各个模块尚不明确的短板。刘扬等[6]利用二项式传递函数描述制导律的脱靶量,在纯延迟的情况下研究了系统延迟对脱靶量的影响。王伟等[7]通过试验分析了激光半主动导引头的角速度噪声特性,得出了激光半主动导引头的角速度噪声为白噪声,并构建了末制导系统伴随模型,以此研究角速度噪声对制导精度的影响。陈阳等[8]利用伴随方法得到了各误差源对脱靶量的影响,结果表明制导精度与自动驾驶仪的动态特性密切相关。王磊等[9]通过构建基于比例导引制导系统的伴随系统,并利用无量纲归一化的方法得到了无量纲脱靶量的表达式,经过仿真表明无量纲脱靶量与制导系统的比例导引系数、阻尼以及带宽有着密切联系。陈天衡[10]在伴随系统的基础上,以降低末端脱靶量为目标,通过构建制导系统输入与脱靶量之间的关系,得到了有关脱靶量的精确的数学解析解。
为了得到在高速拦截背景下所需要的导引头的性能指标,本文在伴随方法的基础上,搭建激光制导的末制导回路,使用伴随方法构造了激光制导回路的伴随系统,仿真分析了随着弹-目接近速度的不断提高,导引头在不同的响应速度下,导引头角速度测量误差、导引头角速度噪声和导引律的角度约束对制导精度的影响。
1 伴随系统的构建
伴随方法是一种基于系统脉冲响应的技术,非线性系统经过一定的近似转化可转变为线性时变系统,从而通过线性时变系统和伴随系统之间的构建方法可获得线性时变系统的伴随系统,两者之间冲击响应解的对应关系可作为分析线性时变系统的基础。
两者之间冲击响应解的对应关系为在原系统的任意初始时刻ti处输入一个脉冲信号,而需要在原系统的终端时刻tf观测在初始时刻输入的脉冲信号对系统造成的影响,此时可将这一过程等效为在原系统对应的伴随系统中,在初始时刻处输入相应的脉冲信号,而在伴随系统的tf-ti时刻处观测输入的脉冲信号对伴随系统造成的影响,原系统与之对应的伴随系统之间除了系统响应在时间轴上为反向之外,两者的脉冲响应是完全相同的。其基本的伴随关系可如下式所示:
h(ti,tf)=h*(0,tf-ti)
(1)
式中:h*为伴随系统中观测到的脉冲响应。
在文献[3-9]中详细分析了如何构建原系统的伴随模型,其主要包含了3个主要的步骤:
①将系统输入转化为脉冲输入。对于一个有确定输入的系统,可以通过将原系统的确定输入转化为脉冲输入来构建导弹的伴随系统,假设原系统在ti时刻输入的确定输入为阶跃响应,通过在伴随系统中的零时刻输入脉冲,然后积分获得具有确定输入系统的伴随系统的构造如图1所示。图中,a为确定输入的值,δ(0)为冲激信号。
对于一个白噪声输入的制导系统,若要分析噪声对制导精度的影响,通常是由蒙特卡洛仿真试验的方法来实现,而采用蒙特卡洛的方法,则需要进行大量的仿真试验才能获得噪声对制导精度的影响。在伴随系统的构造中,白噪声驱动线性时变系统产生的均方响应为通过对伴随系统脉冲响应的输出进行平方并积分。含有白噪声输入的伴随系统转换如图2所示。图中,Φ为白噪声的功率谱密度。
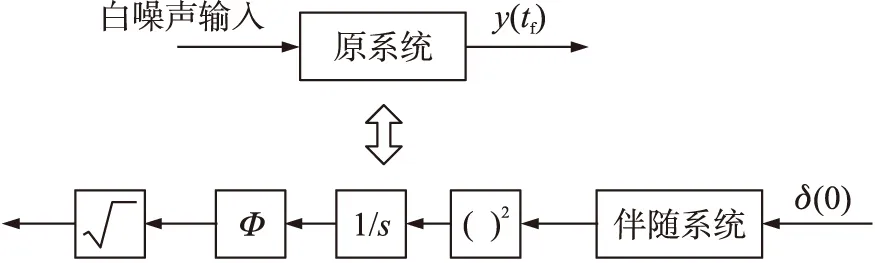
图2 含有白噪声输入的伴随系统转换
②在所有含时间参数的变量中将t用tf-t替代,tf为系统终端时间;
③令所有信号流向反向,将原分支节点改为求和点,将原求和点改为分支节点,将原系统的输入量改为输出量,输出量改为输入量。信号流反向示意图如图3所示。图中,G为传递函数。
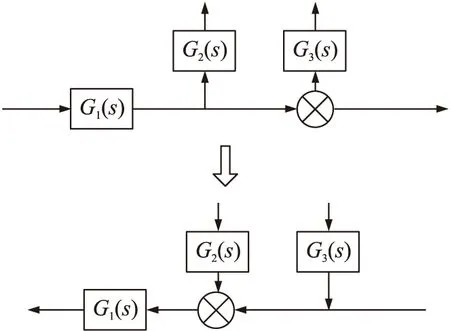
图3 信号流反向示意图
通过以上3个步骤构造出原系统的伴随系统模型,该伴随方法可有效应用于飞行器制导系统的设计和分析。
2 激光末制导系统
2.1 激光末制导回路
采用激光半主动的制导方式,激光导引头由激光探测系统、陀螺稳定系统、信息处理控制系统组成。激光探测系统采用透射式光学系统和PIN四象限探测器组件方案;陀螺稳定系统采用与光电探测系统连接的速率陀螺稳定平台方案。激光导引头系统功能框图如图4所示。
假设导弹速度远大于目标速度,此时可认为目标是静止或低速非机动运动的目标,因此可认为弹-目相对速度vc≈vm[11]。考虑末端攻击角度的比例导引方法,制导回路如图5所示。图中,N为比例导引系数,vm为导弹飞行速度,Yt为目标位移,Ym为导弹位移,vc为接近速度,剩余飞行时间tgo=tf-t,当t=0时,tgo=tf。
激光末制导系统的精度存在诸多影响因素,其中激光导引头的角速度测量噪声、角速度测量误差以及激光导引头的动态特性等都会影响激光末制导系统的精度,而导引头的角速度测量噪声则与导引头的形式有关,不同的导引头产生的角速度测量噪声具有不同的特性,其中激光半主动导引头的角速度噪声为白噪声。
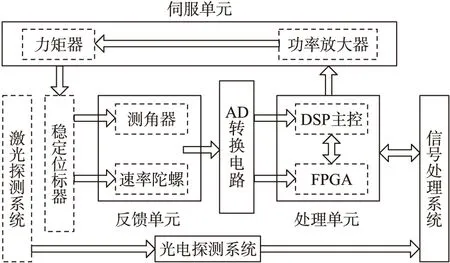
图4 激光导引头系统功能框图
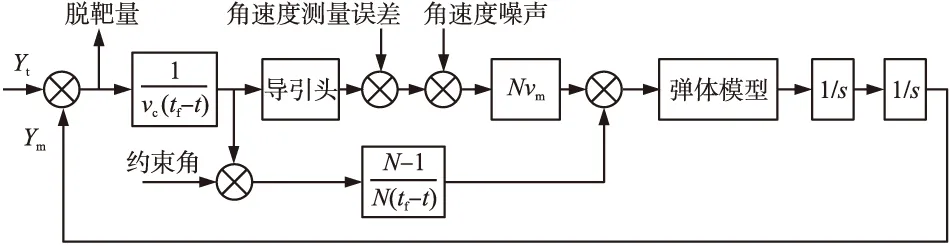
图5 末制导回路
2.2 激光导引头模型
激光半主动比例导引方式具有制导精度高,抗干扰能力强,结构简单且易于实现等优点,因此在高精度制导武器中得到广泛的应用。而激光导引头是激光制导的核心部件,也是制导控制回路的重要测量部件。激光导引头的主要任务是跟踪目标和实时测量弹-目视线角速度。
考虑到制导大回路的频带较低,可以忽略导引头的高频特性,则可对导引头的稳定平台进行模型的简化分析。末制导回路构建的主要目的在于仿真分析导引头的动态特性对制导精度的影响,忽略基座对平台的干扰力矩,包括滚动摩擦力矩以及回路中的非线性环节等因素,可将导引头传递函数Gg简化为如下模型:
(2)
式中:τd为导引头时间常数,可用来描述导引头的动态特性。选取不同τd值,可得到不同响应速度的导引头模型。
2.3 弹体动力学模型
将拥有自动驾驶仪的弹体动力学模型等效为一个二阶系统,其传递函数为
(3)
式中:ξ,ωn分别为弹体阻尼系数和弹体自然频率,具有自动驾驶仪的弹体的动态特性能得到较大改善,其阻尼系数ξ=0.707,自然频率ωn=20 rad/s。
3 制导精度仿真分析
3.1 导引头角速度测量误差对制导精度的影响
通过前面建立的导引头简化模型以及弹体动力学模型,可建立相应的制导回路模型。角速度测量误差会影响导引头输出的视线角速度信号精度,从而会对制导精度造成影响。根据伴随系统的构建方法,可得到包含角速率测量误差输入的末制导回路的伴随模型,如图6所示。
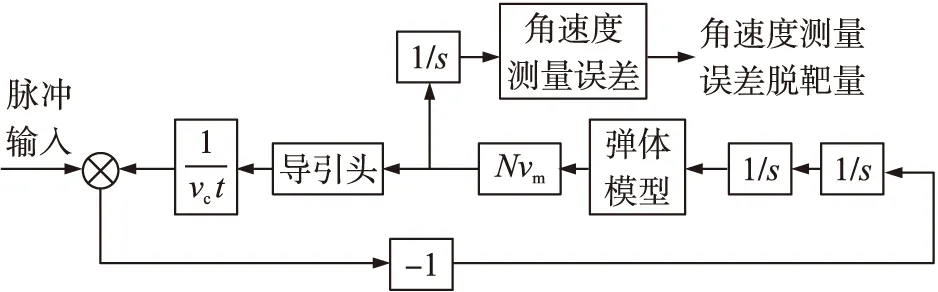
图6 脉冲输入末制导回路的伴随模型
对图6中脉冲输入进行调整,可得转化为单位阶跃输入的伴随系统,如图7所示。
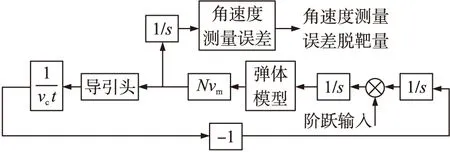
图7 阶跃输入末制导回路的伴随模型
利用图7中的伴随系统可仿真得到导引头角速度测量误差引起的位置脱靶量随末制导时间的变化曲线。
当弹-目接近速度越来越大,需要调节导引头时间常数来改变导引头的响应速度。选取不同的弹-目接近速度和导引头带宽,对角速度测量误差所引起的脱靶量进行仿真,如图8和图9所示。
由图8可知,由导引头角速度测量误差引起的位置脱靶量随着相对末制导时间增大而收敛到0附近,且随着制导弹飞行速度的提高,由导引头角速度测量误差引起的位置脱靶量收敛到零值所需的末制导时间大小没有变化,但导引头角速度测量误差引起的位置脱靶量在收敛过程中的数量级明显增大。
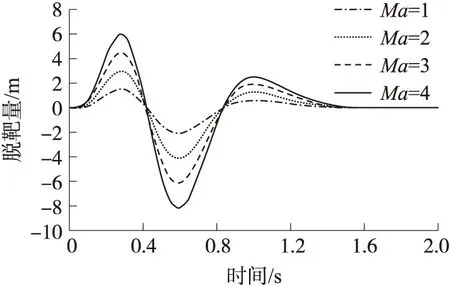
图8 接近速度-脱靶量(角速度测量误差)
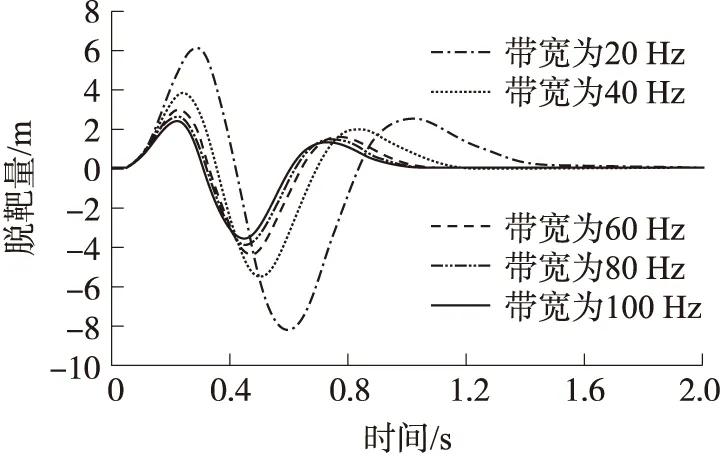
图9 带宽-脱靶量(角速度测量误差)
由图9可知,随着导引头响应速度的提高,也即导引头带宽逐渐变宽,对导引头角速率测量误差引起的位置脱靶量收敛到0所需的末制导时间以及其值都有影响。随着导引头带宽逐渐变宽,导引头角速度测量误差引起的位置脱靶量在收敛过渡过程的数量级有了明显的减小,且导引头角速度测量误差引起的位置脱靶量收敛到0的末制导时间也逐渐缩短。
3.2 导引头角速度噪声对制导精度的影响
激光半主动导引头的角速度噪声为白噪声[16]。可搭建相应的末制导伴随回路,如图10所示。
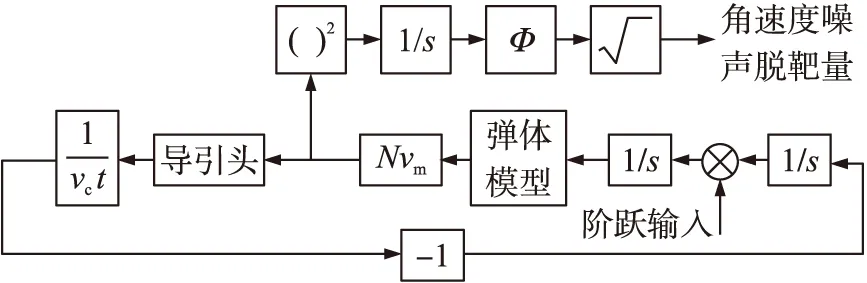
图10 角速度噪声脱靶量伴随回路
通过改变弹-目接近速度可得到图11的仿真结果,从图中可以看出:由导引头角速度噪声引起的位置脱靶量随着末制导时间增大不会趋于0。要保证位置脱靶量趋于稳定,则末制导时间需要足够长。随着弹-目接近速度的提高,对导引头角速度噪声引起的位置脱靶量收敛到0所需的末制导时间大小没有影响,但角速度噪声引起的位置脱靶量在收敛过渡过程中数量级明显增大。
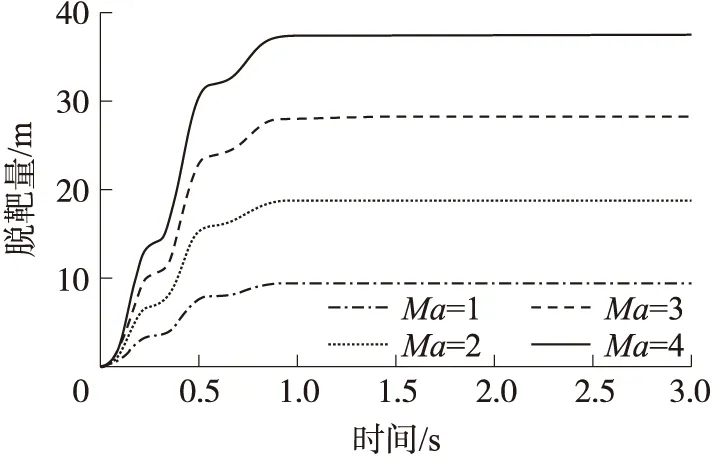
图11 接近速度-脱靶量(角速度噪声)
通过改变导引头时间常数可得到图12的仿真结果。可知随着导引头的响应速度的提高,也即导引头带宽逐渐变宽,对导引头角速度噪声输入引起的位置脱靶量收敛到零值所需的末制导时间以及其值都有影响,导引头角速度噪声引起的位置脱靶量在收敛过渡过程中的数量级有了明显的减小,且导引头角速度噪声引起的位置脱靶量收敛到0的末制导时间也逐渐缩短。

图12 带宽-脱靶量(角速度噪声)
3.3 导引律的角度约束对制导精度的影响
根据图5,可得出由导引律角度约束而引起的脱靶量分析的伴随回路模型如图13所示。
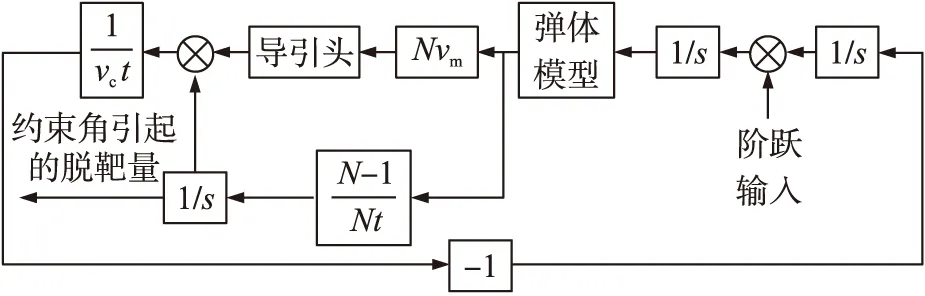
图13 角度约束的脱靶量的伴随回路
通过改变弹-目接近速度可得到图14的仿真结果。从图中可以看出:要保证由角度约束引起的位置脱靶量趋于0,则末制导时间需要足够长。随着弹-目接近速度的提高,对角度约束引起的位置脱靶量收敛到0所需的末制导时间大小没有影响,但角度约束引起的位置脱靶量在收敛过渡过程中数量级有了明显增大。
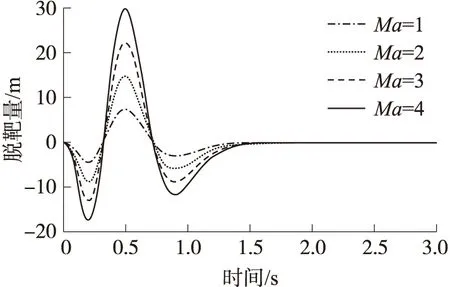
图14 接近速度-脱靶量(角度约束)
通过改变导引头时间常数可得到图15的仿真结果。从图中可以看出:随着导引头的响应速度的提高,对角度约束引起的位置脱靶量收敛到0所需的末制导时间以及其值都有影响,随着导引头带宽逐渐变宽,角度约束引起的位置脱靶量在收敛过渡过程中的数量级明显减小,且角度约束引起的位置脱靶量收敛到0的末制导时间也逐渐缩短。
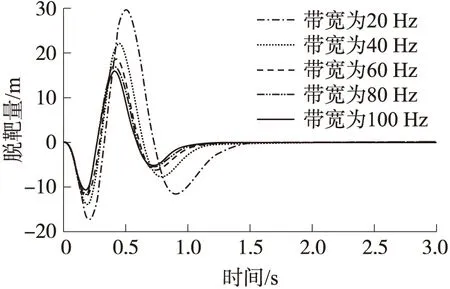
图15 带宽-脱靶量(角度约束)
可见导引头的角速度测量噪声及导引律角度约束对制导精度的影响较大,其引起的脱靶量的数量级也较高,而随着弹-目接近速度的提高,各因素所引起的脱靶量也会相应的提高,通过提高激光导引头的响应速度可以有效降低弹-目接近速度提高带来的影响,而调整导引头的带宽的改善效果也会有一个上限,由图9、图12和图15可知,当导引头带宽达到80 Hz时,改善效果基本达到上限。
4 结束语
在高速拦截过程中,弹-目接近速度的提高对制导精度的影响大,对导引头的性能要求也更高,通过提高激光导引头的响应速度可以有效降低弹-目接近速度提高所带来的影响,结合仿真图对比分析可知,若弹-目接近的马赫数达到4以上,导引头带宽至少大于80 Hz,才能够使得制导精度不会随着接近速度的提高而进一步降低。

