基于摄动理论的动态弹道偏差阈值修正方法
吴汉洲,高 敏,王 毅,杨玉良,董 磊
(1.陆军工程大学石家庄校区 导弹工程系,河北 石家庄 050003; 2.陆军工程大学石家庄校区 火炮工程系,河北 石家庄 050003;3.中国人民解放军66069部队,河南 洛阳 471000)
简易制导方法对硬件性能要求相对不高,常被应用于弹道修正弹上,主要包括弹道成型法、弹道追踪法及弹道预测法等[1]。其中弹道预测法具有较明显优势[2],该方法主要分为弹道落点预测和弹道落点偏差预测。其中弹道落点预测主要通过弹道积分[3-4]、多项式拟合[5]、神经网络[6-8]等方法计算落点,但存在计算量偏大或计算精度差等缺点。李超旺等[9-11]研究了基于摄动理论的落点偏差预测方法在火箭弹、高旋榴弹上的应用,仿真计算及射击试验均验证了该方法满足实时解算要求,且计算精度高。但现有文献对该方法的弹道修正策略鲜有说明,传统设置方法中,当落点偏差大于修正阈值时弹道修正执行机构开始工作,但该修正阈值大小的设置存在较多问题:阈值太小,修正执行机构一直工作,导致电机发热严重,甚至烧坏;阈值太大,弹道修正不足,落点散布较大。本文基于摄动落点偏差预测方法研究了实际应用中与之相关的系列问题,包括摄动落点偏差预测理论模型的推导、基准弹道快速计算方法、偏导数计算方法及数据量的论证,提出了一种动态弹道偏差阈值修正方法,可有效提高弹道修正效率。
1 摄动落点偏差预测原理
将理想条件下从弹丸发射点到目标点的弹道称为基准弹道,在综合射击误差因素下,弹丸实际弹道围绕基准弹道摄动变化,通过在基准弹道不同位置设置扰动误差计算该误差下弹丸落点偏差,将该落点偏差与扰动误差的比值称为该误差因素对落点偏差的敏感因子。
1.1 摄动落点偏差预测理论模型
用r(x,y,z,vx,vy,vz)描述弹丸不同时刻飞行状态,则标准弹道落点可描述为关于各时刻飞行状态的函数:
T=f(r)
(1)
将实际弹道落点描述为
T′=f(r′)
(2)
式(1)和式(2)均为连续函数。不同时刻弹丸实际弹道参数围绕标准弹道参数摄动变化,且两者差值一般不大,则根据泰勒级数收敛性质,可将实际弹道在基准弹道同一位置处泰勒展开,能够满足收敛条件。其理论公式可描述为
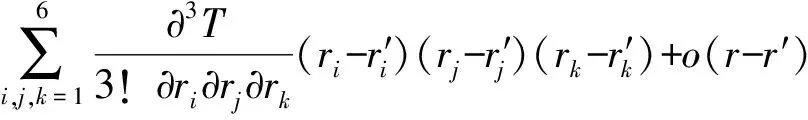
(3)
式中:i,j,k对应r中不同状态变量,o(r-r′)为泰勒级数高阶小量。偏导数∂T/∂ri,∂2T/(2!∂ri∂rj)和∂3T/(3!∂ri∂rj∂rk)即为敏感因子。
对于弹丸不同时刻的偏导数:
(4)
(5)
式中:P表示偏导数,其为关于r的变量的函数。在某一时刻不同阶状态变量的偏导数无排序差异下,式(3)可改写为
(6)
式中:ΔT为实际弹道落点与标准弹道落点的偏差,因高阶小量对落点偏差计算影响较小,可忽略。
1.2 模型参数数值求解
根据有限差分法和偏导数的定义,不同阶偏导数可用如下公式求解[11]:
(7)
式中:Δri和Δrj为对应不同状态变量的偏差。限于篇幅,本文只给出了一阶和二阶偏导数的求解方法,更高阶偏导数按照类似方法也可求解。如果以弹丸飞行距离作为偏导数求解位置参考,则一阶偏导数在弹道纵向x和横向z上各有关于y,z,vx,vy,vz的5类偏导数。而使用二阶偏导数预测落点偏差时还需增加关于上述5种弹丸飞行状态变量两两之间的偏导数,在x和z方向上各有20类偏导数。
2 模型参数论证分析
在实际应用中,射击前需利用火控计算机解算射角诸元、基准弹道和偏导数。为满足快速装定和实时计算要求,在不影响落点精度的前提下,火控计算机和弹载计算机的计算量要尽可能少。
2.1 基准弹道
2.1.1 基准弹道快速计算
计算基准弹道前需首先确定火炮射角θ和射向角α,传统查阅射表或计算机插值计算方法的误差较大,本文基于摄动理论提出了一种修正步长自适应的射角诸元计算方法。
首先计算不同初速、不同射角诸元以及不同气象条件下的弹丸落点,并以数据库形式保存在火控计算机中,基于线性插值法调用该数据库,利用该数据库计算弹丸落点误差不能超过0.4%。在实际应用中,首先通过输入弹丸初速、气象数据及射距L查找数据库,得到一组粗略的射角θn和射向角αn,n为调用数据库和解算弹道模型总次数。该角度与拟求解的精确的射角和射向角误差不大,则可做如下近似:
(8)
(9)
基于θn和αn计算更准确的射角诸元步骤如下:
①基于θn和αn解算刚体弹道模型得到落点T′(xn,zn),计算其与目标点(即标准弹道落点)T(xt,zt)的偏差ΔT(Δxn,Δzn);
②再次调用数据库计算射距L下偏差量为ΔT(Δxn,Δzn),对应的射角和射向角调整量Δθn和Δαn,设θn=θn+Δθn,αn=αn+Δαn,基于新的θn和αn,再次解算弹道模型得到落点T′(xn,zn),设其与T(xt,zt)的偏差为ΔT(Δxn,Δzn);
③设Δθn=(Δθn-1/Δxn-1)Δxn,Δαn=(Δαn-1/Δzn-1)Δzn,则θn=θn+Δθn,αn=αn+Δαn,基于新的θn和αn再次解算弹道模型得到落点T′(xn,zn),其与T(xn,zn)的偏差为ΔT(Δxn,Δzn),重复本步骤,直至ΔT(Δxn,Δzn)满足误差要求。
该方法特点是射角和射向角修正偏差可根据落点偏差大小自适应改变,能够在短时间内计算出满足精度要求的射角诸元,并获得基准弹道数据。

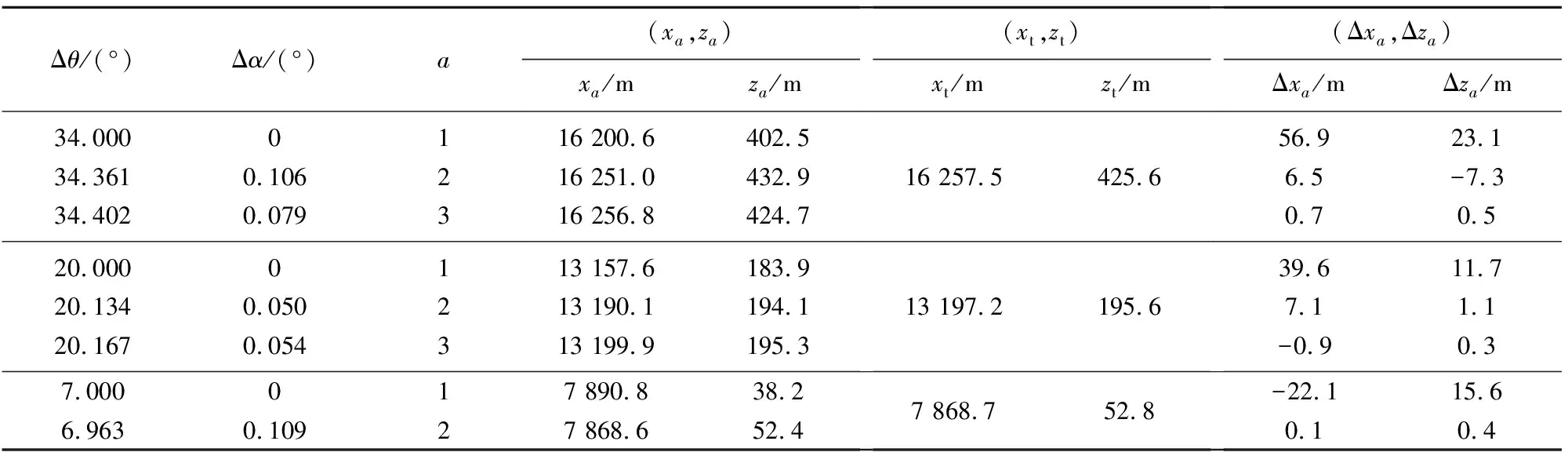
表1 射角和射向角搜索结果
2.1.2 基准弹道数据量
基准弹道数据以矩阵形式装定给引信,矩阵列分别代表基准弹道的y,z,vx,vy,vz等参数,矩阵行表示不同距离的上述参数值。装定给引信的基准弹道行数越少,则基准弹道数据距离间隔越长,这会增大插值误差,影响落点偏差计算精度,而数据间隔太小会增加数据装定量,影响装定速度。
设置射角θ=35°,弹丸开始预测时间为发射后12 s,弹丸落点偏差预测结果如图1所示,弹丸实际纵向落点偏差为65.13 m,横向落点偏差为8.90 m。从图1(a)可看出,基准弹道分别取30行、40行时,纵向落点偏差预测波动幅值分别约为2 m,1 m;基准弹道分别取50行、60行时,偏差波动幅值均不超过0.5 m。从图1(b)可看出,不同基准弹道行数对横向落点偏差预测影响不大,预测偏差波动幅值均不超过0.1 m。因此,θ=35°时选取50行基准弹道数据量较合适,其他射角射击时依此方法论证分析。
2.2 偏导数模型参数
2.2.1 偏导数求解中弹道偏差设置
给刚体弹道模型不同参数添加随机误差,模拟实际应用中存在的射击误差,主要射击误差设置如表2所示。蒙特卡罗打靶仿真计算1 000组弹丸落点,统计计算得弹丸纵向密集度为1/273,比弹丸实际密集度1/278略大,横向密集度为1/1 444,比弹丸实际密集度1/1 467略大,根据误差适当增大原则,表2中射击误差设置满足该型弹最大射角射击时的落点散布规律要求。
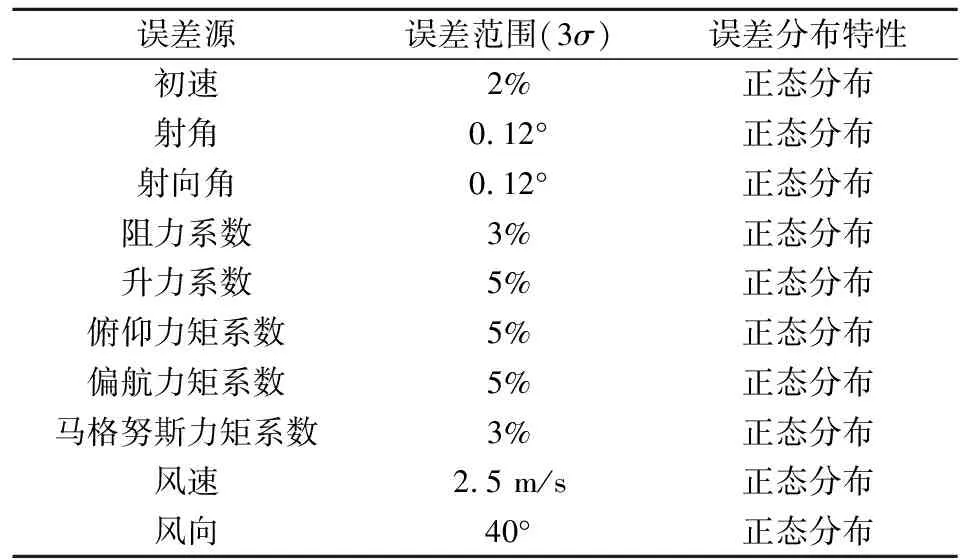
表2 主要射击误差设置
基于表2射击误差,利用蒙特卡罗打靶法仿真计算1 000条误差弹道,将误差弹道与标准弹道比较,得到不同射距下弹丸弹道误差,将同一位置处的1 000个弹道误差取绝对值后再求和取平均值,得到不同射距下弹丸位置平均误差如图2所示,弹丸速度平均误差如图3所示。
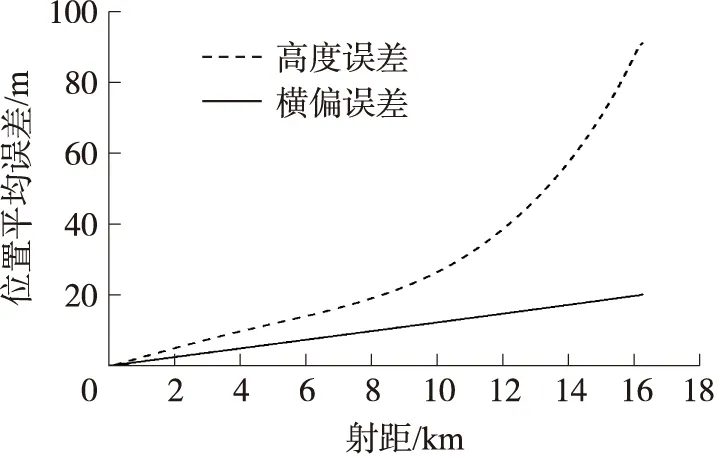
图2 弹丸位置平均误差
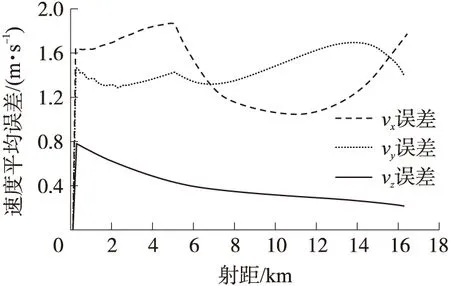
图3 弹丸速度平均误差
从图2和图3可看出,位置平均误差随着飞行距离的增加而增大,而速度平均误差在一定范围内波动变化。为确保偏导数求解精度,在求解弹丸位置偏导数时需根据弹丸飞行距离设置不同偏差值,偏导数求解中弹道偏差设置如表3所示,由于速度误差变化较小,故选用同一偏差值。
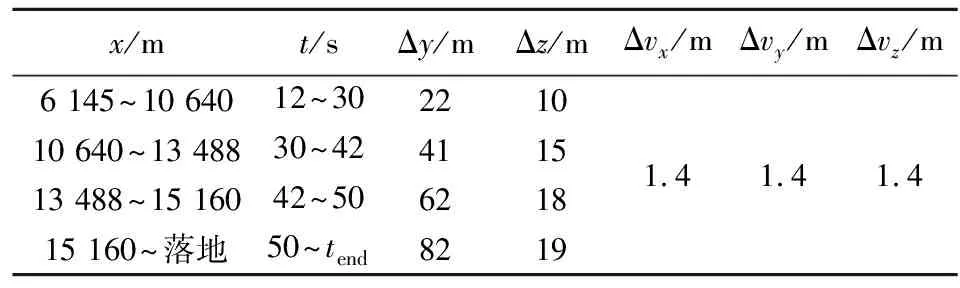
表3 偏导数求解时弹道偏差设置
图4为弹丸纵向落点偏差Δx分别为13.23 m,65.13 m,115.43 m时,利用不同弹道偏差求解的偏导数对落点偏差预测精度的影响。其中“小步长”对应的弹道位置偏差为Δy=22 m,Δz=10 m(下同);“大步长”对应为Δy=82 m,Δz=19 m(下同);“变步长”设置如表3所示,速度偏差设置均为Δvx=Δvy=Δvz=1.4 m/s(下同);弹丸横向落点偏差Δz分别为1.77 m,8.90 m,16.04 m时,利用不同弹道偏差求解的偏导数对落点偏差预测精度的影响如图5所示。
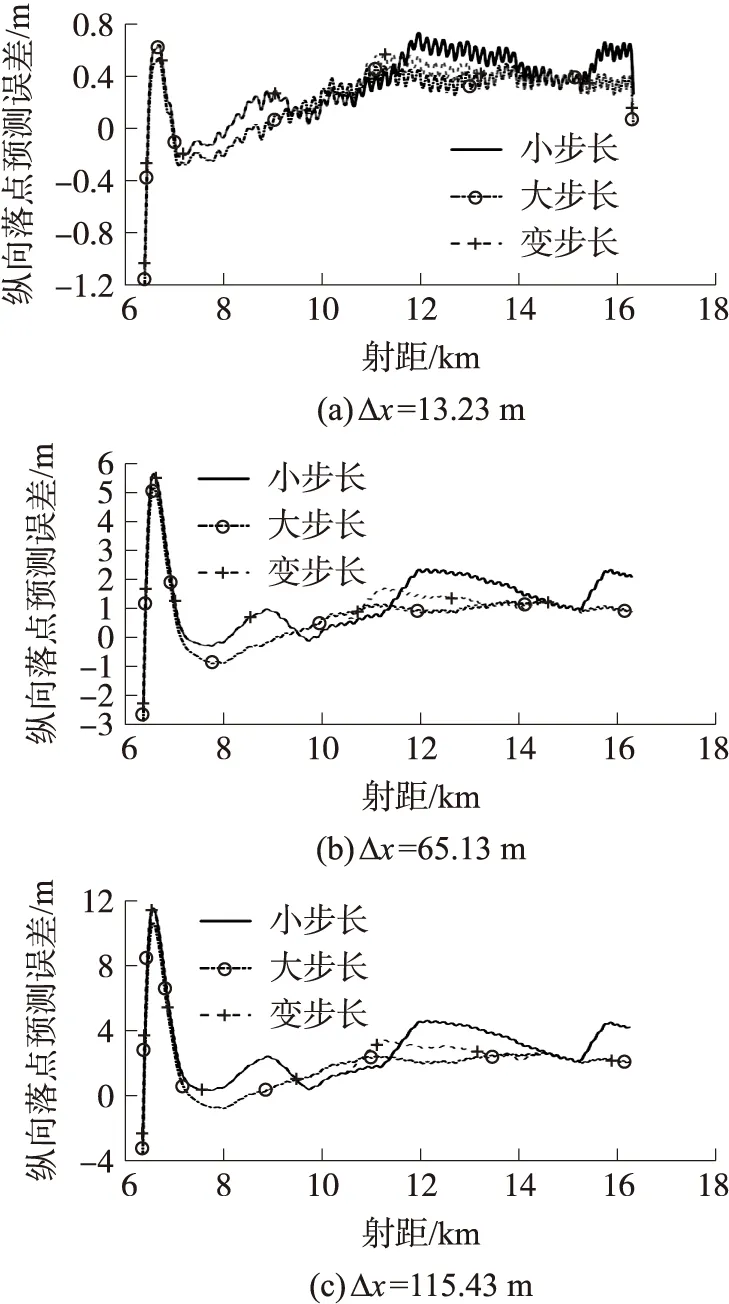
图4 纵向落点偏差预测精度
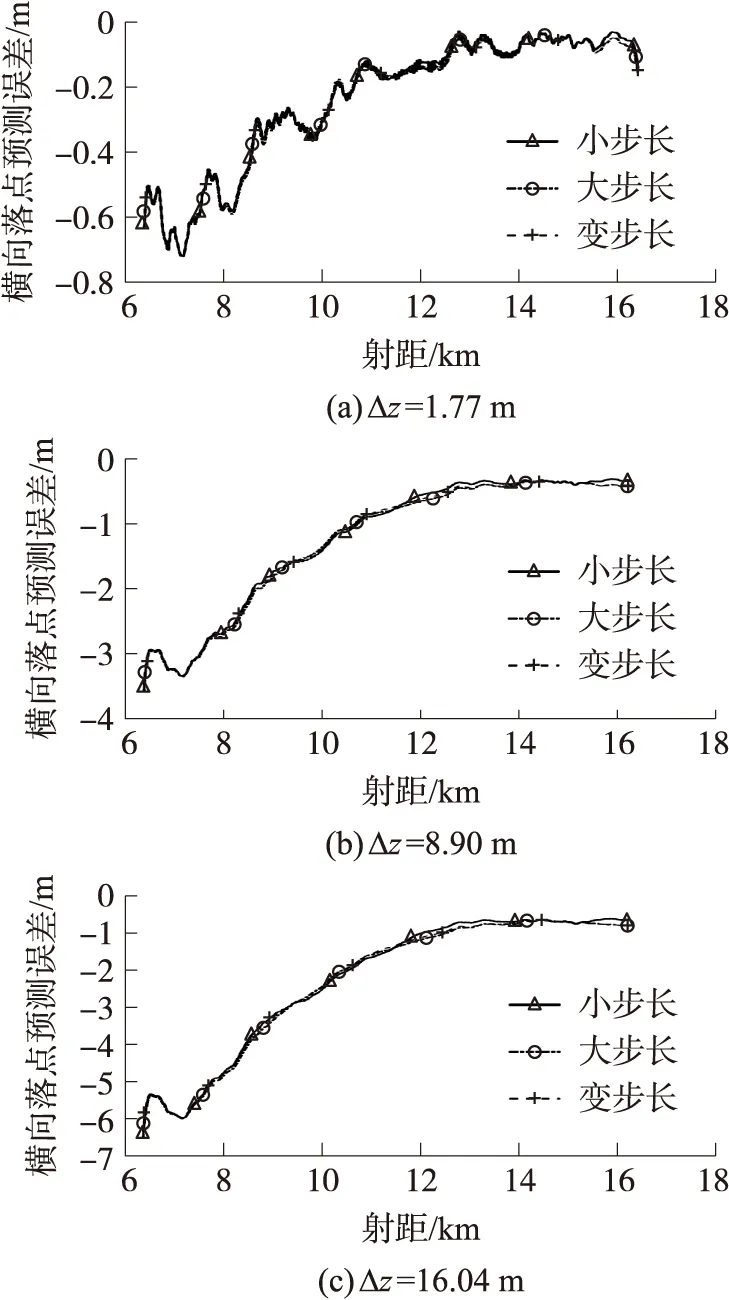
图5 横向落点偏差预测精度
从图4可看出,在初始预测阶段误差较大,但随着弹丸飞行,预测误差快速减小,并达到收敛;小步长设置下,在弹道前期预测精度较高,随着弹道偏差的增大,预测误差开始大于大步长和变步长;大步长参数设置下,在弹道前期预测精度偏低,随着弹道偏差的增大,预测精度慢慢好于小步长;变步长参数设置下,预测精度结合了小步长和大步长参数设置下的优点,在全弹道上预测精度都较高。从图5可看出,随着落点偏差的增大,落点预测精度也整体降低,但误差都保持在较小水平,这主要是因为弹丸横向落点散布较小,横向落点偏差与弹道偏差满足较好的线性关系。
2.2.2 偏导数阶数
根据泰勒级数展开理论,保留的偏导数阶数越高落点偏差预测精度越高,但由于弹道测量偏差的存在,计算中引入的测量误差也可能更大。图6为分别利用一阶偏导数和二阶偏导数预测落点偏差的精度的比较。
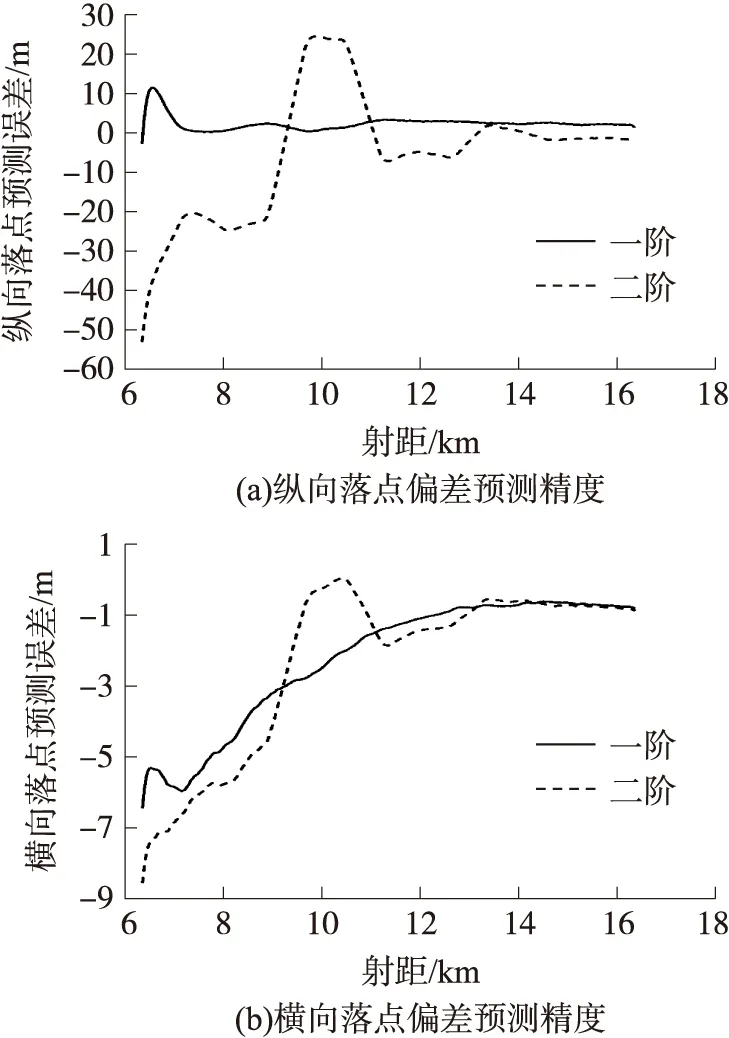
图6 不同阶偏导数预测落点偏差精度比较
从图6(a)可看出,使用一阶偏导数预测弹丸纵向落点偏差精度较稳定,误差一般不超过2 m;使用二阶偏导数预测纵向落点误差收敛速度慢,且波动幅值较大。从图6(b)可看出,使用一阶偏导数预测弹丸横向落点偏差精度较稳定,误差逐渐收敛,最终误差与二阶偏导数预测精度相当;使用二阶偏导数预测误差,收敛速度快,但误差波动较大。综上分析,选用一阶偏导数预测弹丸落点偏差。
2.2.3 偏导数数据量
与基准弹道数据形似,计算出的偏导数也是以矩阵的形式装定给引信,只是矩阵的列表示不同弹丸飞行状态参数的偏导数,矩阵的行依然表示不同射距上对应的偏导数。偏导数行数少,则不同行的偏导数射距间隔大,容易造成落点偏差预测精度差。
图7为使用不同行数偏导数预测弹丸落点偏差的精度的比较。从图7(a)可看出,偏导数行数越多纵向落点偏差预测精度越高;10行和15行偏导数预测精度差别不大。从图7(b)可看出,使用不同行数偏导数预测弹丸横向落点偏差的精度差异不大,特别是在弹道后期,预测精度基本一致。综上分析,兼顾落点偏差预测精度和精度收敛速度,选10行偏导数较合适。
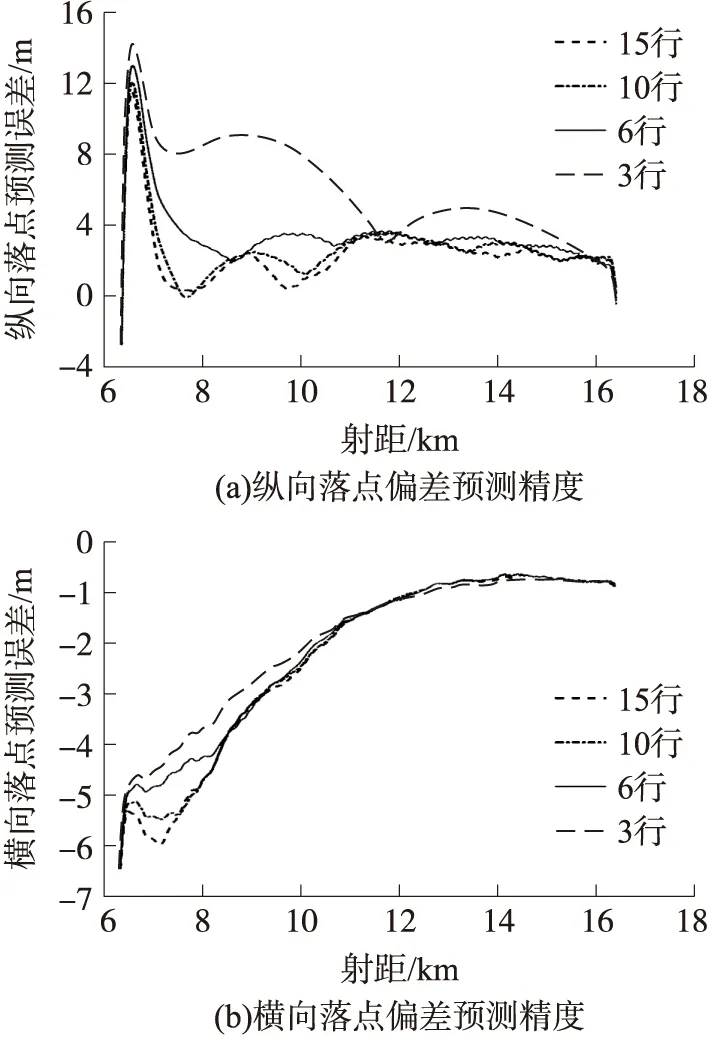
图7 不同行数偏导数落点偏差预测精度比较
3 动态弹道偏差阈值修正
基于摄动理论计算出弹丸落点偏差后,需将该偏差与弹道偏差阈值进行比较,确定是否进行弹道修正。传统方法将阈值设置为一个定值Wxz,当落点偏差大于Wxz时进行弹道修正,反之不修正。
3.1 修正能力分析
以105 mm固定舵式二维修正弹为例,弹丸不同飞行时刻,固定舵弹道修正能力如图8所示,弹丸飞行约25 s达到弹道顶点。从图8可看出,固定舵在弹道升弧段修正能力较强,且对弹丸的横向修正能力大于纵向修正能力;在弹道降弧段修正能力下降明显,弹丸对弹道纵向修正能力略大于横向修正能力。因此,在制定弹道修正策略时要优先修正纵向落点偏差。
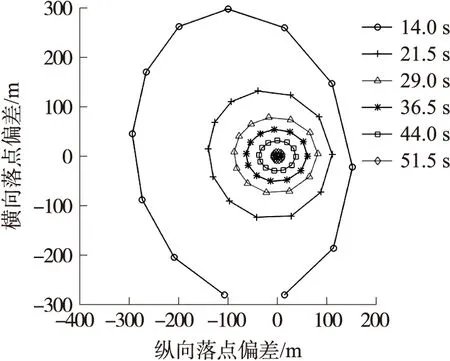
图8 弹丸不同时刻修正能力
3.2 动态弹道偏差阈值的选择
根据弹丸不同时刻修正能力确定基于时间序列的动态弹道偏差阈值,如表4所示。表中,Wx为弹道纵向偏差阈值,Wz为弹道横向偏差阈值。利用蒙特卡罗打靶法仿真计算修正弹道,记录每条弹道的修正次数,统计全部弹道总修正次数和落点散布规律。仿真计算参数设置如表5所示。
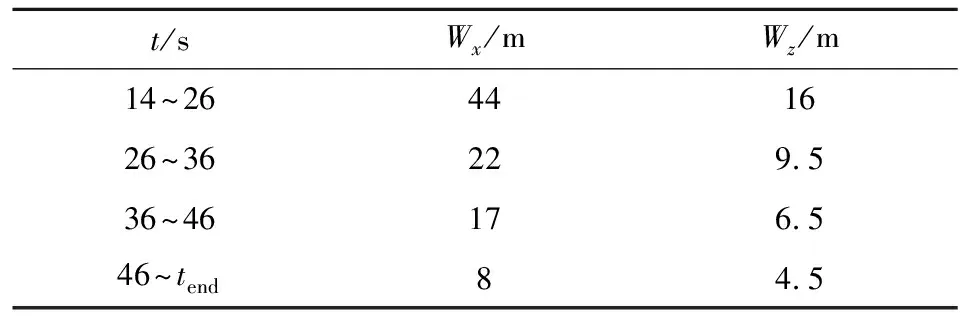
表4 弹道偏差修正阈值表
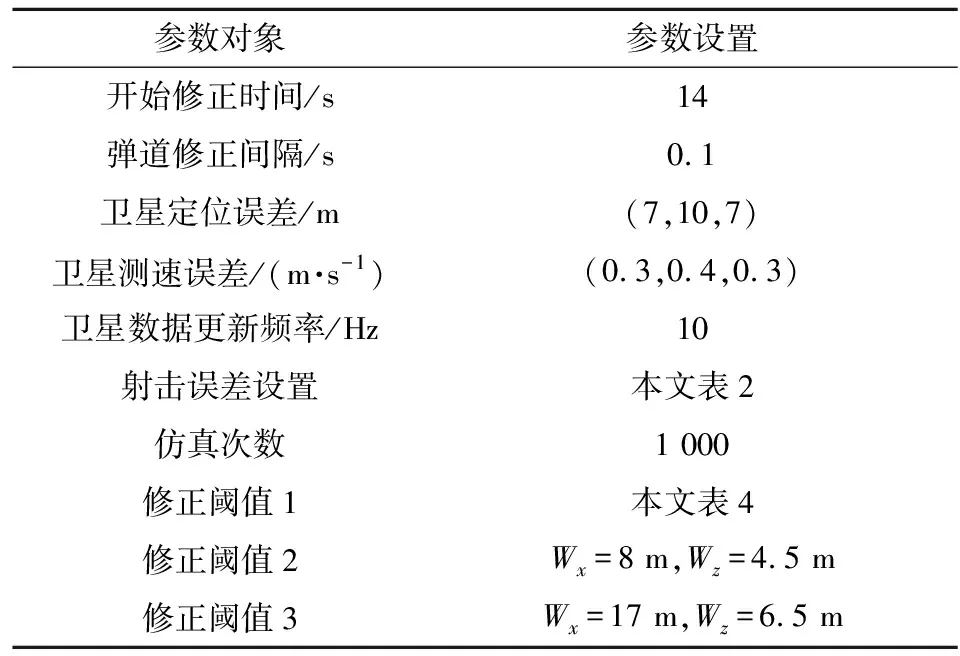
表5 仿真计算参数设置
不同修正阈值设置对应的弹丸落点散布如图9所示,对应圆概率误差(CEP)及总弹道修正次数如表6所示。
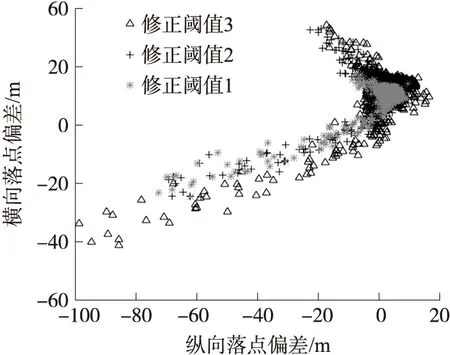
图9 弹丸落点散布对比

表6 不同修正阀值下弹道修正结果
从图9可看出,修正阈值1与修正阈值2对应的弹丸落点散布规律相似,修正阈值3对应的落点散布较大。从表8可看出修正阈值1与修正阈值2落点CEP基本相同,但前者总弹道修正次数较后者减少29.1%,修正阈值3弹道总修正次数较修正阈值2减少,但仍大于修正阈值1,且其对应的落点CEP显著增大。因此,选用动态弹道偏差阈值进行弹道修正能够在不影响弹丸落点CEP条件下有效减少弹道修正次数,提高弹丸全弹道修正效率。
4 结束语
本文以多元函数的泰勒级数展开为理论依据,推导了摄动落点偏差预测方法理论模型,并给出了相关偏导数的求解方法。针对摄动落点预测方法实际应用涉及的相关技术问题,提出了基于摄动理论的修正步长自适应快速求解射角诸元的方法,该方法依托火控计算机循环解算弹道模型得出目标解,具有循环次数少,求解速度快的特点;为提高摄动落点预测精度,给出了偏导数求解中弹道偏差的设置方法;为提高弹道修正效率,基于舵片不同弹道时刻修正能力,提出了以飞行时间为序列的动态弹道偏差阈值修正方法,选用该方法进行弹道修正,在不影响弹丸落点CEP前提下可降低弹道修正次数29.1%。

