基于气动/弹道耦合的激波针外形优化研究
单继祥,赵 平,龚志斌,陈强洪
(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)
对于以侵彻弹为代表的火箭弹,可通过提高其落地速度,以实现更优的综合性能。因此,在气动布局设计过程中应尽量减小气动外形阻力。在弹体前安装激波针是一种非常简单、有效的超声速减阻方法[1-3]。
激波针的减阻效果与其外形参数密切相关,国内外的相关研究主要集中在激波针的外形参数影响及其优化,包括激波针的长短、不同外形以及不同攻角时的气动性能[4-10]。侯文新等[4]在Isinght优化平台的基础上,以热流和阻力系数最小为目标,开展了激波针外形多目标优化设计。李永红等[5]对多种外形激波针的减阻效果进行了比较,结果表明,半圆形激波针跨、超声速减阻效果最优,但在亚声速将增大阻力。
目前,关于激波针的优化研究主要是针对某一超声速下特定马赫数进行减阻优化,对其他马赫数下的阻力特性不予考虑或设定约束。同时,不同马赫数下激波针外形最优尺寸差异较大。但在火箭弹实际飞行过程中,马赫数遍及低、亚、跨、超声速,覆盖范围较广,单单对某一代表性马赫数下的外形进行优化难以实现性能最佳。
本文采用气动/弹道耦合的优化方法,以具有头部激波针的火箭弹为计算模型,结合试验设计、近似模型、优化算法等技术,以落地速度最大作为优化目标,对激波针外形进行了优化设计,并对不同激波针外形阻力特性、弹道特性进行了对比研究,分析了激波针的减阻、增速机理。该研究为该类飞行器激波针的设计、优化提供了参考。
1 计算模型及弹道特性
1.1 计算模型
本文的计算模型如图1所示。全弹采用尖拱外形头部,旋成体弹身,“×”型尾翼。弹身半径为200 mm,头部尖拱段长度为300 mm。
基于增强减阻效果、降低气动热影响的考虑,激波针采用半球盘外形。该激波针具有半球体头部和旋成体身部。初始激波针球头半径为80 mm,长度为弹身直径的2倍,如图1(b)所示。
图1 计算模型
1.2 弹道特性
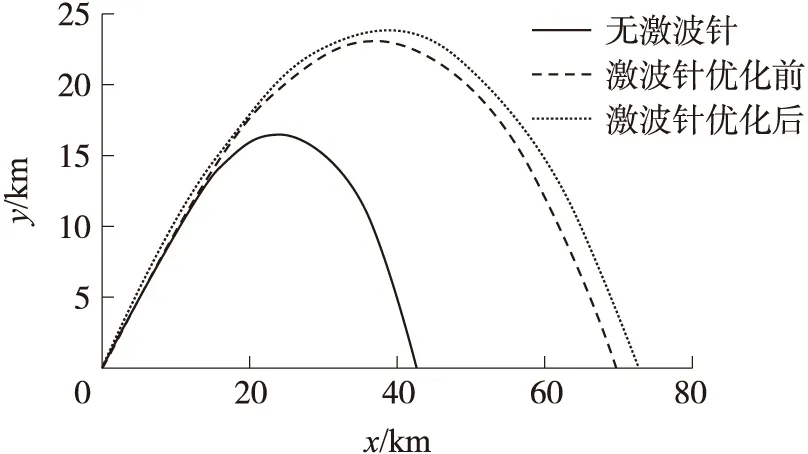
本文计算时采用的弹道为理想条件下的惯性弹道。飞行过程中,全程攻角为0。无激波针时的弹道曲线如图2所示。全弹主动段结束时的速度,即飞行过程中的最大速度约为900 m/s,然后飞行速度逐渐降低,当射程大于15 km后,其飞行速度平均在400 m/s,对应马赫数约为1.2。飞行最大高度为16.5 km,射程为42.4 km。

图2 弹道曲线
2 优化方法
2.1 气动/弹道耦合设计思路
图3为气动/弹道耦合设计思路与传统设计思路的比较。
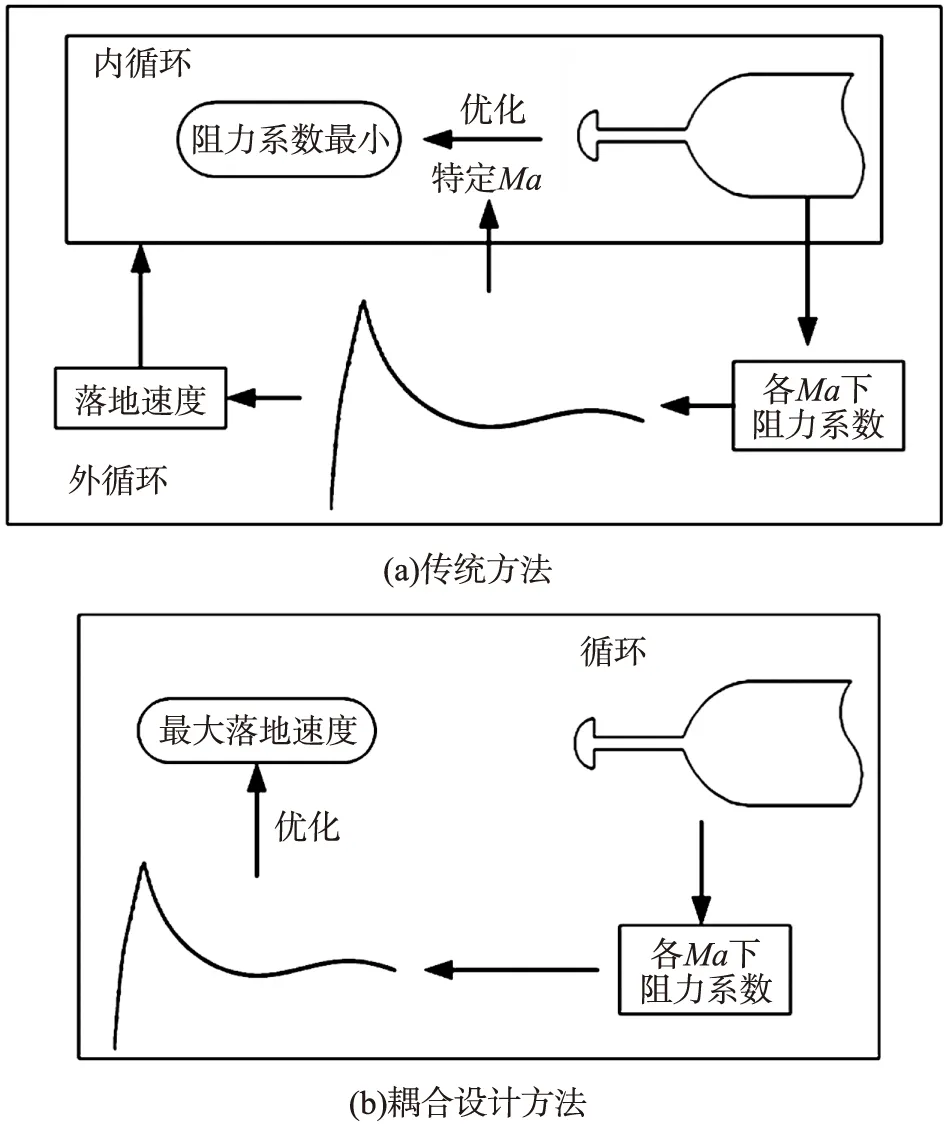
图3 传统设计方法与耦合设计方法的比较
传统的激波针优化设计只针对主要飞行马赫数开展优化,无法考虑全弹道内飞行马赫数对气动优化的影响。气动/弹道耦合设计不是针对特定的弹道飞行马赫数开展优化,而是采用数值模拟方法计算获得某一外形全弹道典型马赫数范围内的阻力系数,并采用以上阻力系数开展飞行弹道计算,获得对应外形的落地速度,即通过气动、弹道的耦合计算获得激波针外形参数与落地速度的直接对应关系,并以落地速度为直接优化目标开展激波针外形优化设计。
2.2 优化方法及流程
2.2.1 优化流程
不同于基于CFD的优化迭代方法,本文采用代理模型建立激波针外形参数与落地速度的预测模型,并采用遗传算法(genetic algorithm,GA)实现满足约束条件下的激波针外形优化,以获得最大落地速度的激波针外形。优化流程图如图4所示。
如图4所示,本文的优化步骤如下:
①利用拉丁超立方采样法在整个计算空间抽样获得N个采样点,建立设计空间里的激波针外形样本方案;
②对N个样本进行几何建模,采用CFD方法计算各样本方案典型马赫数下的阻力系数,并通过弹道仿真获得样本对应的落地速度;
③用各个样本方案的外形参数和对应的落地速度组成样本库,构建两者之间的Kriging代理模型;
④分析代理模型精度,如果精度达不到要求,则回到①,增加样本点数量,提高代理模型可信度,直到模型精度满足要求;
⑤基于以上代理模型,以最大落地速度为优化目标,采用遗传优化方法搜索最优激波针外形,并对该外形开展CFD计算及弹道计算,验证落地速度。
2.2.2 Kriging代理模型
Kriging是一种使用广义高斯方程作为基函数的特殊形式径向基函数插值方法。该方法是根据样本空间的位置与样本之间的关联程度,对不同的样本赋予不同的权值,通过滑动加权平均,从而估计未知空间的样本信息。
Kriging代理模型的预测响应值和均方误差(mean square error,MSE)可以表示为

2.2.3 遗传优化算法
遗传优化算法是一种模拟生物学中进化理论的优化算法。遗传优化算法首先生成初始种群,并计算种群中每个个体的适应度值,判断是否满足终止准则。若满足要求,则停止计算,输出优化最优解;若不满足,则执行遗传算子部分的选择、变异、交叉操作,经过多次迭代实现种群的进化。通过遗传优化算法可获得全局最优解,且不依赖于初值。
2.3 数值模拟方法
全弹气动特性的计算采用基于有限体积法的数值模拟方法,控制方程采用三维雷诺平均Navier-Stoke方程组,其形式如下:
式中:Q为守恒量;F,G,H为无黏通量;Fv,Gv,Hv为黏性通量。数值计算中的湍流模型采用k-ωSST模型。
2.4 计算方法验证
本文对全弹气动力的数值模拟结果和试验结果进行了比较,以验证数值模拟方法和网格的可靠性。
图5是当Ma=1.9时,某模型有、无激波针时阻力系数CD的数值模拟和风洞试验结果比较。可以看出,相同模型时零攻角阻力系数数值模拟结果与试验结果基本一致,且各攻角时激波针减阻量的数值模拟结果和试验结果较为吻合。采用本文的数值计算方法开展激波针优化设计是可行的。
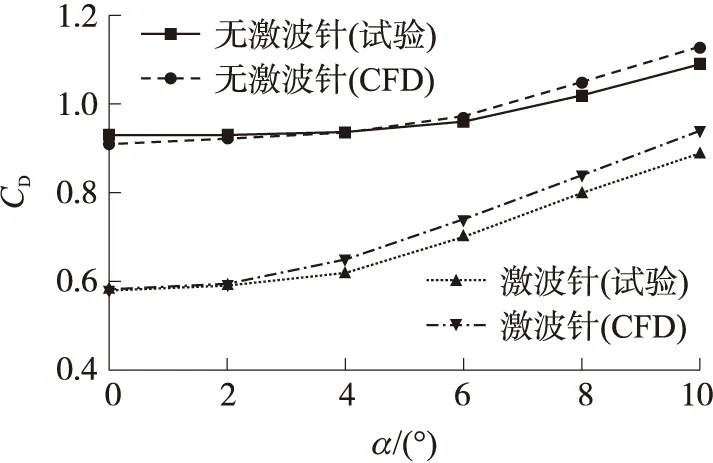
图5 计算结果与风洞试验结果比较(Ma=1.9)
3 优化结果与分析
3.1 不同马赫数下激波针减阻特性
本文首先研究了亚、跨、超声速来流条件下,球头激波针参数对零攻角时全弹减阻效果的影响及其流动机理。
图6、图7分别是零攻角、不同马赫数条件下,激波针长度、头部半径对减阻效果影响的曲线。图中,rp为弹身半径;rs为激波针半径;l为激波针长度。
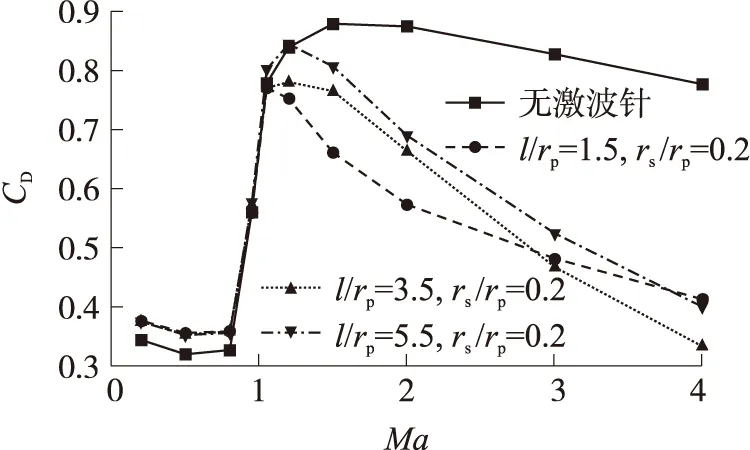
图6 激波针长度对减阻效果的影响
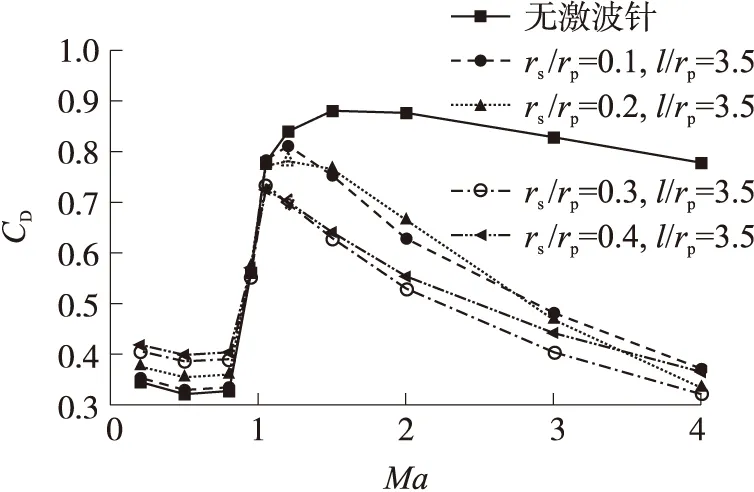
图7 激波针头部半径对减阻效果的影响
从图中可以看出,亚声速时,激波针的存在将导致全弹阻力增加,且阻力增量随着球头部半径的增大而迅速增大,随着激波针长度的增大基本不变。跨声速时,部分外形时,激波针的存在将使全弹阻力减小,合理设计的激波针外形可实现跨声速减阻,但其减阻效果并不明显。超声速时,各参数条件下,激波针均能起到较好的减阻效果,且随着马赫数的增大,相同激波针外形的减阻效果逐渐增强。同时,值得注意的是,各马赫数下的最佳减阻外形不同,随着马赫数的增大,最佳激波针减阻外形的长度逐渐增大。
表1给出了典型马赫数时激波针及弹体的阻力系数。图8是典型马赫数下,激波针外形对称面头部马赫数云图。

表1 典型马赫数时激波针及弹体阻力系数
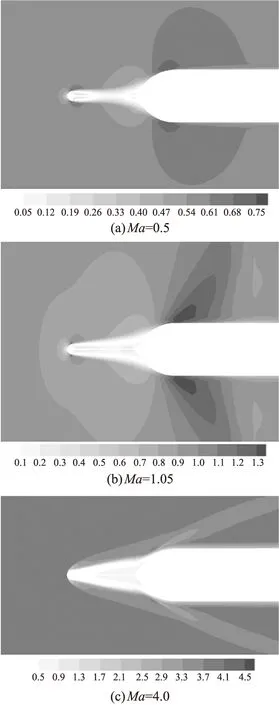
图8 典型马赫数下激波针附近马赫数云图
可以看出,各典型马赫数下,激波针均产生了显著的附加阻力。亚声速时,激波针存在导致弹体阻力小幅增大,加上激波针产生的附加阻力,导致全弹阻力系数增大。跨、超声速时,在头部增加激波针,可消除光头弹体头部弓形激波,使弹体头部波阻减小。跨声速时,弹体阻力的减小量与激波针的附加阻力量值相当,导致激波针的减阻效果有限。随着马赫数的进一步增大,超声速时弹头波阻的减小幅度大于激波针附加阻力的增幅,从而导致全弹减阻量逐渐增大。
3.2 基于落地速度最大的激波针外形优化
针对半球形激波针外形,通过优化激波针球头半径rs及激波针长度l实现减阻,从而提高全弹的落地速度v。
该优化问题可归纳为
优化目标:maxv。
约束条件:射程X>42.4 km。
设计变量:球头半径rs∈[20 mm,80 mm],长度l∈[300 mm,1 100 mm]。
在初始优化外形方面,选取Ma=1.2时(无激波针时弹道主要飞行马赫数)减阻效果较佳的激波针外形参数,rs=80 mm,l=460 mm。
优化前后激波针外形参数如图9所示,其各马赫数下全弹阻力系数曲线如图10所示。通过比较优化前后激波针外形参数,可以看出,优化后激波针长度有所增大,激波针球头半径则有所减小。激波针外形的以上变化将使亚声速、超声速时的阻力系数减小,跨声速时(0.95≤Ma<1.5)的阻力系数增大。由优化前后激波针模型弹道飞行速度曲线的比较(如图11所示)可以看出,与无激波针模型相比,随着主动段(飞行马赫数范围为0.1 图12是有、无激波针模型飞行弹道的比较。从中可以看出,增加头部激波针后,全弹最大飞行高度、射程均大幅增加,提高了该弹的打击范围。与无激波针模型相比,优化后激波针模型最大高度由16.5 km提高到23.7 km左右,射程由42.4 km增大到72.3 km,提高了70.0%。与优化前激波针模型相比,优化后激波针模型射程进一步提高,使激波针对射程的改善效果进一步提高10.0%。这说明激波针优化对射程能力也有提高作用。 图9 激波针优化前后外形示意图 图10 优化前后激波针模型阻力系数比较 图11 有、无激波针模型飞行速度比较 图12 有、无激波针模型飞行弹道比较 对于以惯性弹道飞行(零攻角)的无控弹,要求全弹有较高的静稳定裕度,以减弱风干扰、推力偏心等干扰对落点精度的影响。 图13是典型马赫数下,有、无激波针模型全弹升力系数、压力系数随攻角的变化曲线。可以看出,与无激波针外形相比,优化后激波针模型升力系数CL、压心系数Xp均变化较小。当Ma=4.0时,激波针对纵向气动力影响最大,最大可使升力系数增加0.8%左右,压心系数前移1%。总体而言,增加激波针对全弹升力特性、静稳定特性均影响较小。 图13 典型马赫数下有、无激波针时全弹气动力比较 本文采用数值模拟方法研究了亚跨超声速范围内球头激波针外形参数对减阻效果的影响及其流动机理,并以最大落地速度为优化目标,基于气动/弹道耦合优化方法对激波针外形进行了优化。结果表明: ①亚、跨声速范围内,由于激波针产生的附加阻力较大, 使得全弹阻力系数增大, 激波针无减阻效果;超声速时,激波针的减阻效果明显,且随马赫数的增大,最佳减阻外形的长度增大,半径减小; ②基于气动/弹道耦合的激波针外形优化方法充分考虑了气动、弹道间的相互影响,优化后可使落地速度、射程在基础上进一步提高10.0%左右; ③亚、跨声速范围内,增加激波针对全弹升力特性、静稳定特性均影响较小。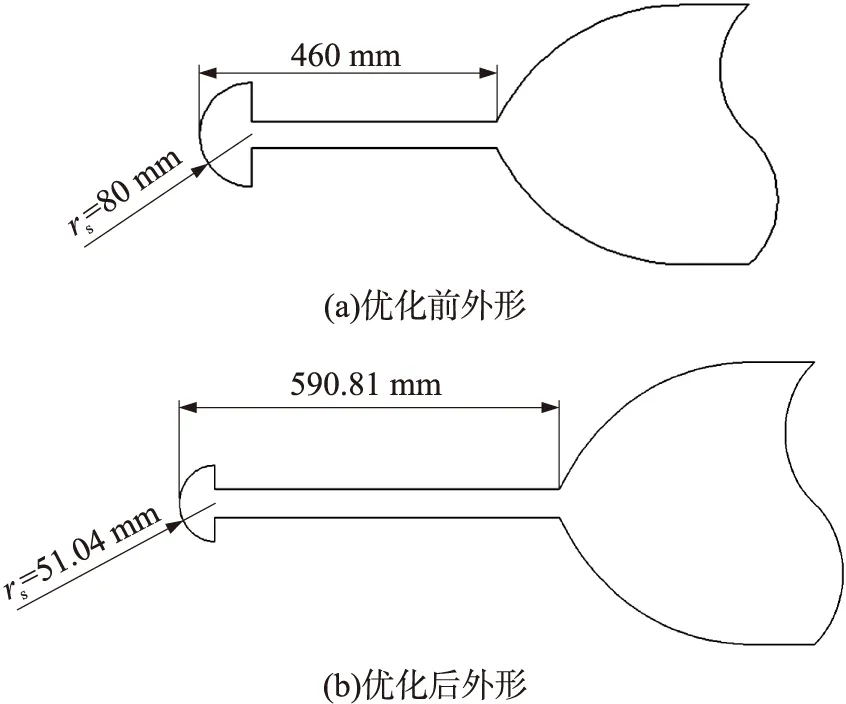


3.3 头部激波针对全弹气动特性的影响

4 结论

