基于迂回相位的轨道角动量Talbot阵列照明器

聂芳松，姜美玲，张明偲，曹耀宇，李向平

基于迂回相位的轨道角动量Talbot阵列照明器

聂芳松，姜美玲，张明偲*，曹耀宇*，李向平

暨南大学光子技术研究院，广东省光纤传感与通信技术重点实验室，广东 广州 510632

轨道角动量(OAM)光束具有螺旋形相位分布，在信息光学、光捕获、光学操控等领域都有着重要的应用。本文设计了一种可以生成聚焦OAM光束的平面型光学器件。该器件利用迂回相位的编码方式，在平板上加载了根据分数Talbot效应计算得到的特定相位分布。使用时域有限差分(FDTD)分别对具有正方形和六边形周期性结构的光学器件进行仿真模拟。结果表明，平面波经过此器件可以转化为阵列型聚焦OAM光束。该器件加工方便，容易拼接或复制，集成度高，可以用来生成高质量大面积阵列型OAM光束。

分数Talbot效应；轨道角动量；周期性结构；迂回相位

1 引 言

光子和经典力学宏观粒子一样，都可以携带能量、动量和角动量。光子的角动量又分为自旋角动量(spin angular momentum，SAM)和轨道角动量(orbital angular momentum，OAM)。自旋角动量是光子的内禀属性，每个光子携带的自旋角动量为±ℏ，表现为偏振光学的左旋或者右旋圆偏振光；轨道角动量是指光在传播过程中，每一个平行的截面上具有exp(i)的螺旋形相位分布，对应的每个光子携带的轨道角动量为ℏ，代表轨道角动量光束的拓扑荷，在理论上可以取值为任意整数，因此每一个光子理论上可以携带无穷种轨道角动量[1]。因此，轨道角动量光束被普遍应用于光通信[2-4]、超分辨[5-6]、纳米操控[7-10]、激光加工[11]和光存储[12-15]等领域。随着光学微纳器件逐步开始由实验室研究阶段发展为大规模工业生产阶段，人们对于OAM光束提出了越来越高的要求。

1992年，Allen等人利用两个柱透镜，首次在实验中产生了轨道角动量光束[1]。目前，轨道角动量光束已经可以通过多种方式产生，例如：通过螺旋相位片法[16-17]、涡旋波片法[18-20]、全息叉形光栅法[21-22]、空间光调制器[23-25]等相位调制方法，都可以在宏观空间中产生OAM光束；通过环形角光栅结构的回音壁模式[26]，表面等离子体耦合-解耦合等手段[27-28]，同样可以在微观空间内产生OAM光束。然而，以上产生OAM光束的方法多用于产生单一OAM光束，无法满足人们对于多焦点大面积阵列型光场的需求。

本文中，我们根据分数Talbot效应，设计了一种可以产生大面积阵列型OAM光束的照明器件。该器件利用迂回相位的编码方式，在平板上加载特定的相位分布。分别讨论了四边形和六边形周期结构生成聚焦OAM光束的理论基础和设计参数，解析了单色平面波入射下，两种周期型相位板生成的轨道角动量光斑强度分布。并使用时域有限差分(finite difference time domain，FDTD)仿真模拟方法对设计的结构进行了进一步的验证。该器件设计简单，具有高集成度，大面积复制拼接等优势，可以方便产生高质量阵列型聚焦OAM光束。

2 基本原理

周期性结构在单色平面波照射下，由于光的衍射，可以产生自成像现象，即Talbot效应[29-30]。简单来说，Talbot效应可以理解为横向周期为的光场，在传播过程中，产生周期为T=22/的纵向周期性；纵向周期T即为Talbot距离，为单色光波长。当周期性光场的占空比为1/时，在周期性结构后方Z=T/2的位置，可以产生一个均匀振幅面，即在这个平面上，光场的强度都是相等的，每个像素之间仅存在相位的差别，这个效应又称之为分数Talbot效应，T/2又称为分数Talbot距离。对于边长为的二维正方形周期性结构，具有类似于一维周期结构的特点。和一维周期结构相似，二维周期结构的Talbot距离T=22/。因此，根据分数Talbot效应，我们设计一种15´15的正方形阵列结构作为周期单元，将15´15空间的入射光聚焦到中心点1´1像素上，即=15；每一个正方形像素基元的边长为unit，根据分数Talbot距离的定义，得到：

如图1(c)所示。对于多元相位分布的Talbot相位板，每一个不同的相位，代表着具有不同光程，也就是不同厚度的电介质结构单元，相位板的厚度分布示意图如图1(d)所示。显然，上述相位板结构具有非常复杂的多阶结构，这种结构难以通过传统的激光直写或者离子刻蚀技术加工而成。

3 结构设计和计算分析

图1 (a), (b) 正方形单周期Talbot相位板的(a)相位分布和(b) l = 1的螺旋相位分布；(c), (d) 叠加轨道角动量的Talbot相位板的(c)总相位分布和其相应的(d)三维立体结构。

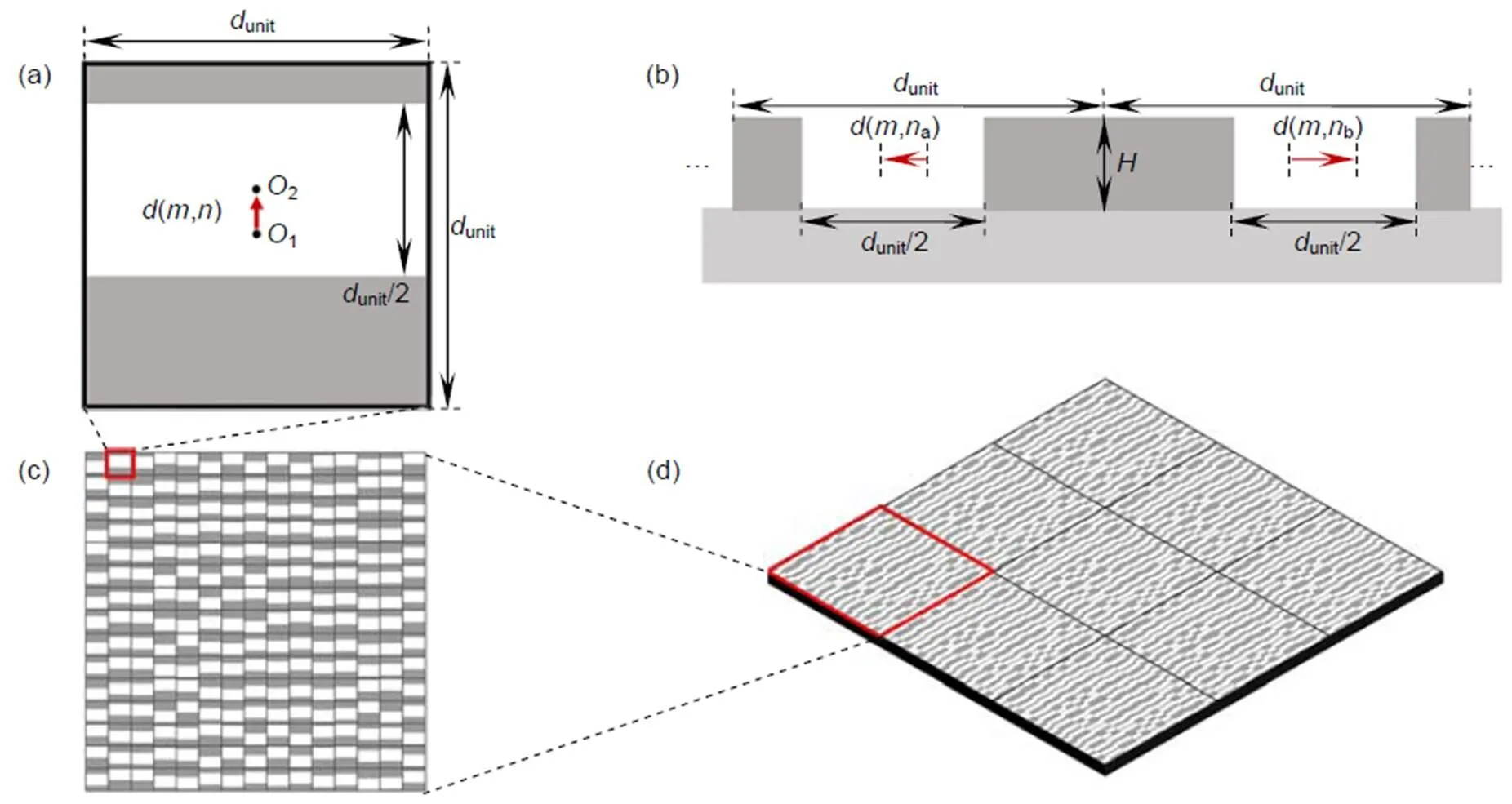
图2 (a), (b) 迂回相位编码Talbot阵列照明器的正方形1´1像素(a)基元结构(其中d(m,n)为0相位中心位置偏移量，O1和O2分别对应基元中心和0相位中心)和(b)位置偏移；(c), (d) 迂回相位编码Talbot阵列照明器的(c)单周期和(d)3´3周期阵列结构

图3 (a), (b) 迂回相位编码的正方形Talbot阵列照明器的(a) l=0和(b) l=+1的电场强度分布；(c), (d) 分别是l=0和l=+1的FDTD模拟仿真计算结果；(e) l=+1的阵列型电场强度分布

当光瞳函数更接近圆域函数，光斑的分布也就更加接近圆形分布。为了进一步优化轨道角动量光斑质量，可以将正四边形的周期性结构替换为正六边形的周期性结构。定义边长为的六边形的光瞳函数为

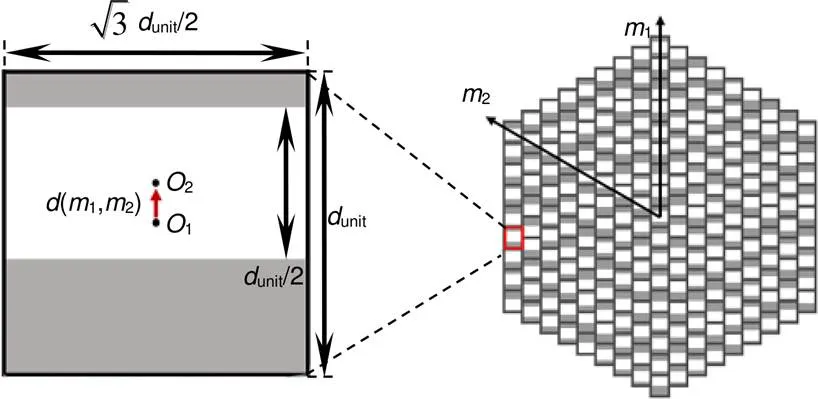
根据倒格子理论，六边形的Talbot参数不完全和四边形等同。对于边长为´unit(表示每一个边都由个像素基元构成)的六边形Talbot阵列照明器，特定的六边形Talbot距离为

对应的分数Talbot距离为

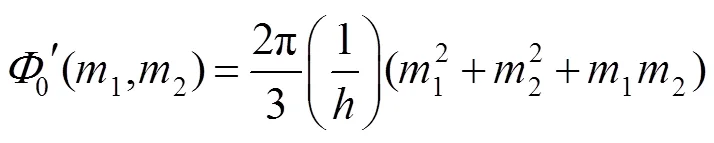
图4 (a) 六边形单周期Talbot相位板的相位分布；(b) l=+1的螺旋相位分布；(c) 迂回相位编码六边形Talbot阵列照明器的1´1像素基元结构；(d) 迂回相位编码的六边形Talbot阵列照明器

图5给出了边长为=15的六边形Talbot照明器上加载不同的螺旋相位时，生成OAM光束的FDTD模拟仿真结果。=0时，聚焦的光斑不携带轨道角动量，是一个中心强度为极大值的实心光斑，半高全宽为0.63 μm，如图5(a)所示；=±1时，聚焦光斑都表现为一个六个强度均匀的“热点”组成的准空心光斑，每个“热点”光斑与坐标原点的距离都是1.0 μm，半高全宽为0.62 μm，环绕一周相位的变化分别为±2π，分别如图5(b)，5(c)所示；=+2时，聚焦光斑仍然由六个“热点”组成，每个“热点”光斑中心与坐标原点的距离仍然是1.0 μm，半高全宽为0.67 μm，环绕一周相位的变化为4π，如图5(d)所示。图5(e)是=+1时的阵列型电场强度分布。和正方形Talbot阵列照明器相比，六边形Talbot阵列照明器生成的光斑更接近于圆形，同时相位分布也更加均匀。因此，使用六边形Talbot阵列照明器，可以生成更高质量的大面积阵列型OAM光束，以满足大规模工业生产的需要。

4 结 论

本文在分析分数Talbot效应的理论基础上，利用迂回相位编码方法，设计了一种可生成聚焦OAM光束的平面光学器件。通过使用FDTD仿真模拟表明平面波经过此器件可以转化为大面积周期性聚焦OAM光束阵列，焦点尺寸与单像素基元相近。随着决定相位分布的像素基元排布从正方形向六边形变化，具有涡旋相位的焦点强度对称性也相应改变。具有较高中心对称性的像素基元排布有利于实现更均匀的照明。该器件设计简单，加工方便，集成度高，可以大面积地复制拼接，在光捕获、光操控、光学加工等领域有很好的潜在应用。

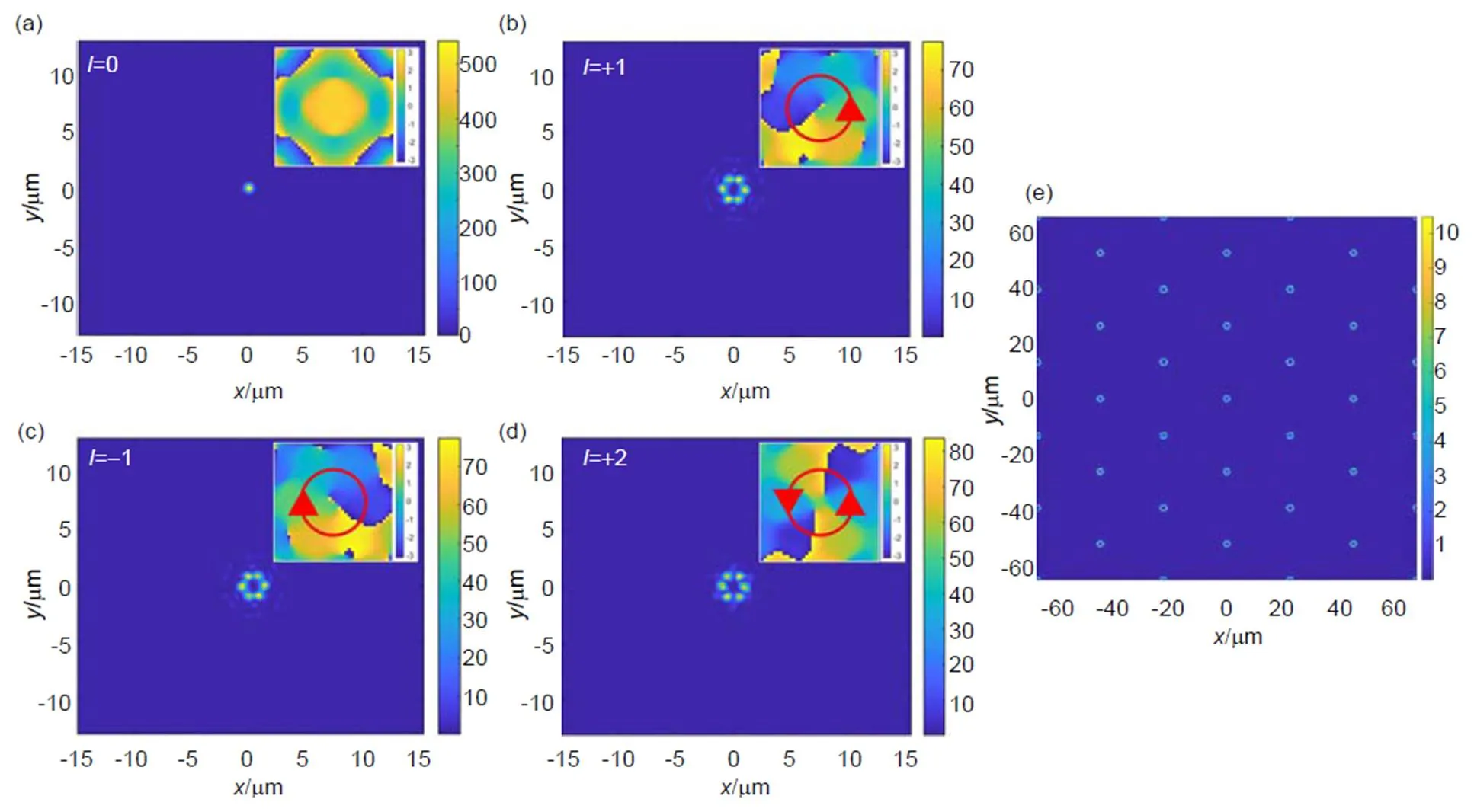
图5 (a) ~(d) 迂回相位编码的六边形Talbot阵列照明器的(a) l=0, (b) l=+1, (c) l=-1和(d) l=+2的归一化电场强度分布；(e) l=+1的阵列型电场强度分布

[1] Allen L, Beijersbergen M W, Spreeuw R J C,. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]., 1992, 45(11): 8185–8189.

[2] Wang J, Yang J Y, Fazal I M,. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]., 2012, 6(7): 488–496.

[3] Bozinovic N, Yue Y, Ren Y X,. Terabit-scale orbital angular momentum mode division multiplexing in fibers[J]., 2013, 340(6140): 1545–1548.

[4] Vallone G, D’Ambrosio V, Sponselli A,. Free-space quantum key distribution by rotation-invariant twisted photons[J]., 2014, 113(6): 060503.

[5] Gan Z S, Cao Y Y, Evans R A,. Three-dimensional deep sub-diffraction optical beam lithography with 9 nm feature size[J]., 2013, 4: 2061.

[6] Cao Y Y, Xie F, Zhang P D,. Dual-beam super-resolution direct laser writing nanofabrication technology[J]., 2017, 44(12): 1133–1145.

曹耀宇, 谢飞, 张鹏达, 等. 双光束超分辨激光直写纳米加工技术[J]. 光电工程, 2017, 44(12): 1133–1145.

[7] Lehmuskero A, Li Y M, Johansson P,. Plasmonic particles set into fast orbital motion by an optical vortex beam[J]., 2014, 22(4): 4349–4356.

[8] Grier D G. A revolution in optical manipulation[J]., 2003, 424(6950): 810–816.

[9] Tao S H, Yuan X C, Lin J,. Fractional optical vortex beam induced rotation of particles[J]., 2005, 13(20): 7726–7731.

[10] Ladavac K, Grier D G. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays[J]., 2004, 12(6): 1144–1149.

[11] Ni J C, Wang C W, Zhang C C,. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material[J]., 2017, 6(7): e17011.

[12] Ouyang X, Xu Y, Feng Z W,. Polychromatic and polarized multilevel optical data storage[J]., 2019, 11(5): 2447–2452.

[13] Li X P, Cao Y Y, Tian N,. Multifocal optical nanoscopy for big data recording at 30 TB capacity and gigabits/second data rate[J]., 2015, 2(6): 567–570.

[14] Ouyang X, Xu Y, Xian M C,. Encoding disorder gold nanorods for multi-dimensional optical data storage[J]., 2019, 46(3): 180584.

欧阳旭, 徐毅, 冼铭聪, 等. 基于无序金纳米棒编码的多维光信息存储[J]. 光电工程, 2019, 46(3): 180584.

[15] Jiang M L, Zhang M S, Li X P,. Research progress of super-resolution optical data storage[J]., 2019, 46(3): 180649.

姜美玲, 张明偲, 李向平, 等. 超分辨光存储研究进展[J]. 光电工程, 2019, 46(3): 180649.

[16] Campbell G, Hage B, Buchler B,. Generation of high-order optical vortices using directly machined spiral phase mirrors[J]., 2012, 51(7): 873–876.

[17] Wei D Z, Wu Y, Wang Y M,. Survival of the orbital angular momentum of light through an extraordinary optical transmission process in the paraxial approximation[J]., 2016, 24(11): 12007–12012.

[18] Beresna M, Gecevičius M, Kazansky P G,. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass[J]., 2011, 98(20): 201101.

[19] Nersisyan S R, Tabiryan N V, Mawet D,. Improving vector vortex waveplates for high-contrast coronagraphy[J]., 2013, 21(7): 8205–8213.

[20] Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]., 2006, 96(16): 163905.

[21] Mair A, Vaziri A, Weihs G,. Entanglement of the orbital angular momentum states of photons[J]., 2001, 412(6844): 313–316.

[22] Wei B Y, Hu W, Ming Y,. Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals[J]., 2014, 26(10): 1590–1595.

[23] Wang X L, Lou K, Chen J,. Unveiling locally linearly polarized vector fields with broken axial symmetry[J]., 2011, 83(6): 063813.

[24] Wang X L, Chen J, Li Y N,. Optical orbital angular momentum from the curl of polarization[J]., 2010, 105(25): 253602.

[25] Wang X L, Li Y N, Chen J,. A new type of vector fields with hybrid states of polarization[J]., 2010, 18(10): 10786–10795.

[26] Cai X L, Wang J W, Strain M J,. Integrated compact optical vortex beam emitters[J]., 2012, 338(6105): 363–366.

[27] Yu N F, Capasso F. Flat optics with designer metasurfaces[J]., 2014, 13(2): 139–150.

[28] Karimi E, Schulz S A, de Leon I,. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface[J]., 2014, 3(5): e167.

[29] Talbot H F. LXXVI.No. Ⅳ[J]., 1836, 9(56): 401–407.

[30] Rayleigh L. XXV.[J]., 1881, 11(67): 196–205.

[31] Zhu L W, Yin X, Hong Z P,. Reciprocal vector theory for diffractive self-imaging[J]., 2008, 25(1): 203–210.

[32] Li Z G, Yang R, Sun M Y,. Detour phase Talbot array illuminator[J]., 2019, 17(7): 070501.

[33] Brown B R, Lohmann A W. Complex spatial filtering with binary masks[J]., 1966, 5(6): 967–969.

[34] Lohmann A W, Paris D P. Binary fraunhofer holograms, generated by computer[J]., 1967, 6(10): 1739–1748.

Orbital angular momentum Talbot array illuminator based on detour phase encoding

Nie Fangsong, Jiang Meiling, Zhang Mingsi*, Cao Yaoyu*, Li Xiangping

Guangdong Provincial Key Laboratory of Optical Fiber Sensing and Communications, Institute of Photonics Technology, Jinan University, Guangzhou, Guangdong 510632, China

(a) The unit cell and (b) one period of hexagonal Talbot array illuminator based on detour phase encoding; (c) Normalized electric field intensity distribution of= +1 for hexagonal Talbot array illuminator

Overview:Orbital angular momentum (OAM) beam with helical phase distribution has demonstrated important applications in information optics, optical storage, laser processing, super-resolution, optical trapping, and optical manipulation. These exceptional achievements heavily rely on the development of OAM micro-devices that can precisely manipulate optical fields of demand. As such functional components gradually reach out to large-scale production for practical applications from the laboratory-scale researches, more requirements are raised for producing OAM beams with equal properties in batches. At present, there are varied methods to generate OAM beams, for example, spiral phase plate method, variable spiral plate method, hologram folk grating method, and spatial light modulator method. However, the above methods are mostly focused on generating a single OAM beam, which overlooks the needs of fostering multi-focus array light field that is highly desirable for novel functions in numerous studies. How to readily realize focused OAM arrays beams over a large area remains a tough challenge from concept to implementation. In this paper, based on fractional Talbot effect, we have designed a planar optical device which can generate periodic array of focused orbital angular momentum beam. The phase distribution of the devised structure contains two parts: the focusing lens phase distribution and the spiral vortex phase distribution. According to detour phase encoding, the phase distribution calculated by fractional Talbot effect is implemented on the planar optical device by discretizing the phase distribution with arrayed phase-control units. The multi-level phase distribution is transformed to the lateral displacement of the rectangular bars from the center of each unit cell, which is proportioned to the phase shift as designed. The focusing property of this optical device with periodic square and hexagonal structures are simulated by finite difference time domain (FDTD). The intensity distribution and phase profile of each single focused light beam in the illumination plane are virtually identical. With changing the arrangement of the phase-regulation unit from square to hexagonal Talbot array, the symmetry of the intensity distribution for the focused light spot with vortex phase distribution changes accordingly. The symmetry of the hexagonal Talbot array is higher than the square counterpart. This optical device with explicit advantages of being easy to fabricate, splice, duplicate, and integrate can efficiently prop up the generation of high-quality large-area array-type OAM beams for widely spreading applications in optical trapping, optical manipulation, optical fabrication, and other fields.

Citation: Nie F S, Jiang M L, Zhang M S,Orbital angular momentum Talbot array illuminator based on detour phase encoding[J]., 2020, 47(6): 200093

Orbital angular momentum Talbot array illuminator based on detour phase encoding

Nie Fangsong, Jiang Meiling, Zhang Mingsi*, Cao Yaoyu*, Li Xiangping

Guangdong Provincial Key Laboratory of Optical Fiber Sensing and Communications, Institute of Photonics Technology, Jinan University, Guangzhou, Guangdong 510632, China

Orbital angular momentum (OAM) beam with helical phase distribution has demonstrated important applications in information optics, optical trapping, and optical manipulation. In this paper, we designed a planar optical device which can generate a periodic array of focused orbital angular momentum beams. Based on detour phase encoding, the phase distribution calculated by fractional Talbot effect is implemented on this planar optical device. The property of this optical device with periodic square and hexagonal structures is simulated by finite difference time domain (FDTD) respectively. The optical device with explicit advantages of being easy to fabricate, splice, duplicate, and integrate can efficiently prop up the generation of high-quality large-area array-type OAM beams.

fractional Talbot effect; orbital angular momentum; periodic structure; detour phase

TM923

A

10.12086/oee.2020.200093

: Nie F S, Jiang M L, Zhang M S,. Orbital angular momentum Talbot array illuminator based on detour phase encoding[J]., 2020,47(6): 200093

聂芳松，姜美玲，张明偲，等. 基于迂回相位的轨道角动量Talbot阵列照明器[J]. 光电工程，2020，47(6): 200093

Supported by National Natural Science Foundation of China (61605061, 61875073), the Natural Science Foundation of Guangdong Province (2016A030313088), and Guangdong Provincial Innovation and Entrepreneurship Project (2016ZT06D081)

* E-mail: mszhang@jnu.edu.cn; yaoyucao@jnu.edu.cn

2020-03-19；

2020-05-09

国家自然科学基金资助项目(61605061，61875073)；广东省自然科学基金资助项目(2016A030313088)；广东省创新创业资助项目(2016ZT06D081)

聂芳松(1994-)，男，硕士研究生，主要从事激光加工微纳结构方面的研究。E-mail：315737726@qq.com

张明偲(1990-)，男，博士，主要从事表面等离子体方面的研究。E-mail：mszhang@jnu.edu.cn曹耀宇(1981-)，男，博士，主要从事超分辨光学技术与应用的研究。E-mail：yaoyucao@jnu.edu.cn