城市轨道交通调线调坡设计系统研究与开发

摘 要：为适应城市轨道交通线路调线调坡设计需求，文章基于线路设计理论和限界标准，通过CAD 二次开发，研发调线调坡设计系统。该系统首先对以结构底板作为测量基准线的测量结果进行修正，然后建立以设计轨面为坐标系横轴的各结构断面类型的方程式，快速准确地对限界进行检查。该系统采用的数据以隧道结构底板作为测量基准线，自动对测点数据进行修正并进行限界检查工作，能大大减小现场测量工作者的工作量，提高设计工作效率。

关键词：城市轨道交通;线路设计;调线调坡;CAD 辅助设计

中图分类号：U212.32

1 调线调坡设计概述

调线调坡设计是土建结构完工之后，轨道铺设和设备安装之前的一项重要工作。土建施工往往存在误差，与设计方案不一致。为消除由于隧道、车站等土建结构中心线偏离设计线位产生的影响，避免产生侵入限界的情况，工程师会依据测量结果，与理论限界值进行对比，分析偏差大小和趋势，在原设计线位基础上进行线路调整，再重新检查限界侵限情况，直至限界满足要求。当调线调坡也无法消除施工误差的影响时，就需要对土建结构进行改造或者调整设备安装位置。

在调线调坡设计方面，袁士涛等提出基于点云数据实现地铁限界检测及调线调坡设计自动化的研究思路 [1]，任博文进行了城市轨道交通调线调坡测量软件的开发[2]，蒋勇提出采用空间圆拟合法对调线调坡测量中圆形隧道横断面进行拟合[3]，黄铂清提出基于遗传算法的调线调坡优化设计方法[4]，李家稳提出地铁调线调坡设计中基于距离法和面积法的优化算法[5]，李家稳、张海燕等提出地铁调线调坡双边线形约束模型[6]，明杰进行了调线调坡计算方法的研究[7]，杨亢亢等对隧道施工偏差和限界监测进行了研究[8]，孔令洋对地铁限界系统的设计原理进行研究并开发了限界设计软件[9]，孟凡铁、陈菊对深圳地铁调线调坡工作进行总结并研究了相关技术[10-11]，司耀旺、许兆俊结合工程调线调坡实践提出了调线调坡设计关键技术[12-13]。但以上研究中调线调坡的测点数据均是以设计轨面为坐标系横轴进行测量得到的数据，测量员需在隧道内先放样线路中心线再进行隧道断面测量。

本文利用AutoLisp、C++等，在AutoCAD2014平台上开发了城市轨道交通调线调坡设计系统，系统包括项目管理、线路参数设置、水平限界检查、竖向限界检查4个功能模块。本文介绍该系统以隧道结构底板数据作为测量基准线的测点数据修正方法，水平、豎向限界检查模块的开发，以及研究中涉及的原理。

2 测量数据修正

2.1 隧道偏移修正

城市轨道交通线路在市区或建筑密集区常采用的工法是盾构法，圆形盾构隧道和马蹄形隧道断面通常是结构专业的标准断面。根据GB 50157-2013《地铁设计规范》 第5.3.5条和CJJ/T 96-2018《地铁限界标准》，圆形或马蹄形隧道在曲线超高地段，应采用隧道中心向线路基准线内侧偏移的方法，解决轨道超高造成的内外侧不均匀位移量。其中竖向位移量按如下公式计算：

式（1）～（2）中，z'为隧道中心竖向位移;h0为隧道中心至轨顶面的垂向距离;h为轨道超高;α为由于轨道超高而产生的车辆中心线与坐标轴之间的夹角，α = sin-1（h /s）;s为左右轮滚动圆间距。

2.2 实际隧道底板竖向偏差修正

实测隧道底板和设计底板高程往往是存在偏差的，调线调坡设计中需以实际隧道底板作为测量基准线，然而此时基准是一个无规律的基准线，设计线路中心线却是一条线形完好的空间曲线。通过建立实测隧道底板数据与设计底板数据的数据关系，就可以将实测隧道结构底板数据转化成以设计轨面线为基准的数据。将实测隧道底板数据与设计底板数据之差记为?h，则各测点数据减去?h，即可得到以轨面高程数据作为基准线的数据。

图1 给出了实际施工断面上、下浮动示意图，图中虚线代表设计隧道，实线代表实测隧道。图1a为实测隧道较设计隧道上浮的情况，表示实测隧道底板高程大于设计隧道底板高程，需将测点高程减去|?h|;图1b为实测隧道较设计隧道下沉的情况，实测隧道底板高程小于设计隧道底板高程，需将测点高程加上?h。设?h=设计隧道底板高程H设计 -实测隧道底板高程H，?h即为底板侵限值（隧道下沉时，?h>0;隧道上浮时，?h<0），则对实测隧道底板高程进行修正后得到的测量基准线高程H修正 为：

设计隧道底板高程由设计轨面高程、隧道偏移量或者隧道加宽量、轨道超高方式和轨道结构高度共同决定，计算出设计隧道底板与实测隧道底板的竖向偏差并进行测点修正，就可将以实测隧道底板为基准的测点数据转化为以轨面高程为基准的数据。

3 隧道限界方程

3.1 矩形隧道建筑限界方程

（1）直线地段矩形隧道建筑限界方程。矩形隧道建筑限界坐标系的建立方法为建立正交于轨道中心线的平面直角坐标，如图2所示。以2根钢轨轨顶中心线连线的中点o引出的水平坐标轴作为y轴，以通过该中点垂直于水平轴的纵轴作为z轴， h1为设计轨面至隧道顶板的距离，h2 为设计轨面至隧道底板的距离，b1为线路中心线至隧道左边墙的距离，b2为线路中心线至隧道右边墙的距离。建立矩形隧道限界方程如下：

（2）曲线地段矩形隧道建筑限界方程，如图3所示。列车在曲线上运行时作为一个刚性结构不能随曲线弯曲，列车转向架中心线与线路中心线不重合，同时曲线上设置的超高使得车体向曲线内侧偏移。以A型车为例，矩形隧道内外侧加宽值E内、E外 按下列公式计算：

当线路左转时，线路中心至左边墙的限界值应在直线段限界的基础上加上E内，线路中心至右边墙的限界值应在直线段限界的基础上加上E外;当线路右转时，与左转情况相反。

3.2 圆形隧道建筑限界方程

（1）直线地段圆形隧道建筑限界方程。圆形隧道限界方程建立方法同矩形隧道限界方程，如图4所示，建立其方程如下：

（2）曲线地段圆形隧道建筑限界方程。圆形隧道在曲线超高地段，应采用隧道中心向线路设计线内侧偏移的方法解决轨道超高造成的内外侧不均匀位移量，如图 5所示，位移量按下列公式计算：

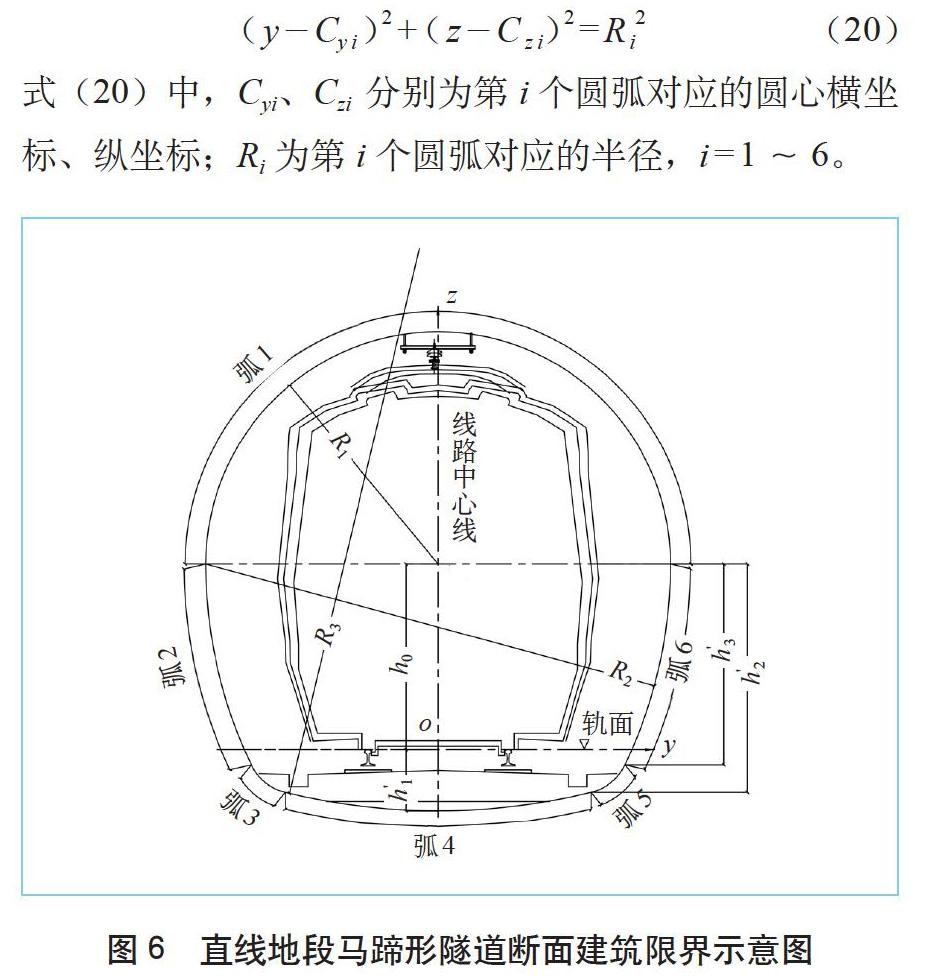
3.3 马蹄形隧道建筑限界方程

4 系统框架设计

调线调坡系统包括项目管理、线路参数设置、水平限界检查、竖向限界检查4个功能模块。系统通过用户输入的平纵断面数据、断面类型和轨道结构高度、轨道超高类型等数据，首先建立各断面建筑限界方程并进行数据修正，将以实测隧道底板为基准线的数据转化为以轨面高程为基准线的数据;再判定断面位于何种线元段落，确定超高值、加宽值或偏移值的修正系数（直线上修正系数为0，圆曲线上为1，缓和曲线上进行线性内插）;最后根据实测数据与理论限界数据之差判定侵限情况。如果限界不满足要求，则需重复进行平纵断面调整设计，重新判定侵限情况直至满足限界要求。调线调坡系统设计流程如图8所示。

5 结束语

本文采用AutoLisp、C++语言等编程技术开发了城市轨道交通调线调坡系统，该系统可直接在AutoCAD2014平台加载运行，并支持32或64位操作系统。该系统在深圳地铁各线调线调坡设计实践表明，以隧道结构底板作为测量基准线进行调线调坡，大大减小了现场测量和限界检查工作量和工作效率。

随着测量技术日新月异，基于绝对坐标的结构断面测量，对结构断面进行三维拟合，实现提取任意位置的断面尺寸，并结合BIM技术对轨道交通线路限界边界进行三维建模，通过三维限界检查自动地进行线路调线调坡设计是今后研究的方向。

参考文献

[1]袁海涛，何涛. 基于点云数据在地铁限界检测及调线调坡设计自动化的研究[J]. 北京测绘，2017（ 增1）.

[2]任文博. 城市轨道交通调线调坡测量软件开发与应用[J]. 北京测绘， 2015（3）.

[3]蒋勇. 城市轨道交通调线调坡测量中圆隧道横断面测量方法的探讨[J]. 城市勘测，2011（1）.

[4]黄铂清. 地铁限界CAD及调线调坡设计系统研究与开发[D].湖南长沙：中南大学，2011.

[5]李家稳，张海燕，韩宝明. 地铁调线调坡中双边线形约束方法的研究[J]. 铁道学报，2010，32（5）.

[6]李家稳. 地铁线路平、纵CAD及调线调坡设计技术的研究[D].北京：北京交通大学，2005.

[7]明杰. 地铁调线调坡计算方法研究[D].湖南长沙：中南大学，2013.

[8]杨亢亢，刘羽劼，薛喆，等. 地铁隧道施工偏差限界检测软件开发与应用[J]. 城市轨道交通研究，2015， 18（5）.

[9]孔令洋，梁青槐. 地铁限界CAD系统设计及开发研究[J]. 都市快轨交通，2004（6）.

[10] 孟凡铁. 深圳地铁调线调坡技术研究[J]. 铁道标准设计，2004（3）.

[11] 陈菊. 城市轨道交通线路设计中的调线调坡技术研究[J]. 铁道标准设计，2014（3）.

[12] 司耀旺. 地铁线路调线调坡设计探讨[J]. 现代城市轨道交通，2016（3）.

[13] 許兆俊. 城市轨道交通平、纵断面设计中的调坡调线[J]. 铁道标准设计，2003（9）.

[14] 周旭. 地铁调线调坡设计方法探讨[J]. 现代城市轨道交通，2015（4）.

[15] 吴永进，林美樱. AutoLISP&DCL基础篇[M]. 北京：中国铁道出版社，2002.

[16] GB 50157-2013 地铁设计规范[S]. 2013.

[17] CJJ/T 96-2018地铁限界标准[S]. 2018.

[18] 欧阳全裕. 地铁轻轨线路设计[M]. 北京：中国建筑工业出版社，2007.

[19] 吴爽，田连生. 地铁平纵面CAD系统研究与开发[J]. 铁道勘察，2014，40（3）.

收稿日期 2019-09-23

责任编辑 朱开明