动态精密单点定位在铁路勘测上的应用研究

董颖略

摘 要：利用2020年实测双频GNSS观测数据，对动态精密单点定位的精度进行验证和评估。与后处理差分软件进行比较，结果显示动态精密单点定位在每个方向上均能获取厘米级的定位准度，其主要偏差体现在高程方向;同时卫星几何空间分布极大的影响动态精密单点定位的结果，相比单一的GPS系统，融合GLONASS的观测数据能较大的改善该问题。通过对上述结果进行分析得出动态精密单点定位可以在铁路勘测等领域进行推广应用。

关键词：动态精密单点定位;GNSS精度;GPS+GLONASS双系统

0引言

随着测绘科学的发展，大量的先进仪器和技术应用到铁路勘测、施工和监测的应用中。GNSS作为新兴的测绘技术在铁路测绘事业中得到了广泛的应用[1]。其中RTK技术由于操作效率和可靠性较高等优点，在地形图测绘、施工放样等领域受到了青睐[2]。但RTK技术的应用需要与基准站同时进行观测，并携带电台发射改正数，这便大大限制了其工作范围。而且在部分高山峡谷地带，RTK技术不能正常工作[3]。精密单点定位技术的出现有望解决这一问题[4]。静态精密单点定位技术已经得到了大量的验证，其定位准确度与高精度差分定位技术相当[4-6]。但目前对于动态精密单点定位技术在实地的应用研究较少，大部分是基于静态模拟动态[7]。基于上述情况，本文对动态精密单点定位技术的准确度进行实地研究，并根据相关结果分析得出相应的结论。

1 动态精密单点定位原理

卫星信号在传播的过程中会涉及到许多误差因素的影响，那么接收到的观测量必须对这些误差加以修正，这些误差主要包括：卫星天线相位中心、卫星端天线相位转绕、相对论效应、电离层延迟、对流层延迟、接收机天线相位中心和地球自转。忽略部分误差，简化后基本的码和相位观测量方程如下[8]：

式（1）中，P表示伪距观测量，L表示转化成距离的相位观测量，下标1和2表示不同频率，I表示电离层延迟;Trop表示对流层延迟;N则表示模糊度;f表示频率;λ表示对应频率波长;tr与ts分别表示接收机和卫星钟差，其中卫星钟差采用IGS 30s产品;c表示光速;ρ表示几何距离，其隐含的卫星轨道坐标也由IGS精密产品提供。

为方便消电离观测量进行解算，则需要对其进行线性化。经过线性化后，等式左边为已知量，等式右边则是关于待求参数的线性表达式，每个历元待求参数可以用下述公式表示：

式中xk，yk，zk分别表示k时刻需求的位置参数，dt表示接收机钟差，ztd表示对流层天顶延迟，N表示对应卫星的模糊度参数，1至m表示卫星。

利用最小二乘或者卡尔曼滤波均可对线性化后的等式进行求解，这里仅列举采用卡尔曼滤波的解算步骤。标准的卡尔曼滤波包含2个步骤，分别为预测和更新，如下式[9]：

其中上标为“-”的表示预测;X表示待求的参数;Ф表示上个时刻到当前时刻的状态转移，对于动态精密单点定位可将该矩阵设置为单位阵;w为未考虑的误差;P表示协方差阵，初始历元协方差阵由经验值确定，后续则根据卡尔曼滤波进行传递;Q表示过程噪声，对于模糊度如不发生周跳则为一常数，故其过程噪声为0，对流层过程噪声可设置为1cm/sqrt（hour），对于位置和接收机钟差参数则可设置较大的噪声;K表示增益;H表示待求參数的系数阵R表示观测量的测量噪声矩阵，测量噪声主要与高度角相关，伪距和相位噪声比值设为100∶1;Z表示上述消电离层观测量线性化后的等式左边;I表示阶数与待求参数个数相同的单位矩阵。

2 试验数据及方案

数据采集工作于2020年3月进行。为与RTK进行比较，总共利用3台GNSS接收机，其中基站采用LEICA GX1230接收机，流动站接收机则均采用LEICA GS15接收机，3台接收机天线均为LEIAX1202GG型内置天线。基站架设于新建银西铁路的CPI控制点上，流动站则在附近先静止后运动，运动过程中随机反复，最后又回到原地，采样率均为15秒。其中LEICA GX1230接收机只能接收GPS信号观测量，LEICA GS15接收机则能同时接收GPS和GLONASS信号观测量。为获取基站的准确位置，基站接收机观测时间约为2小时，其坐标由高精度软件静态解算得到，并与往期的坐标进行比较。在差分解算时将基站坐标作为已知值，解算出流动站的坐标，这一过程利用LGO软件完成。同时利用西南交大PLAOD软件进行动态解算流动站的坐标，PLAOD软件所有解算均为非差模式，里面包含动态精密单点定位模块[10]。

3 解算结果及分析

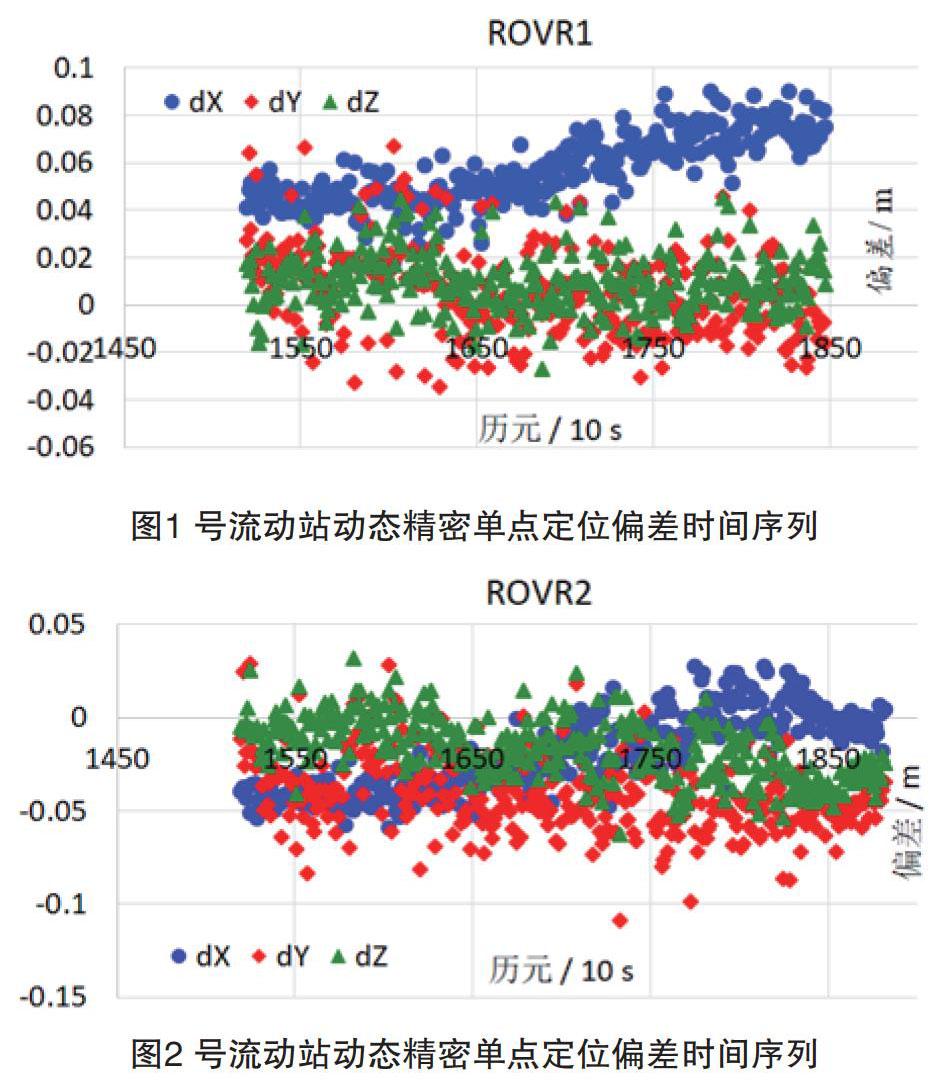
首先利用PLAOD解算两个流动站的GPS观测量，确保观测时段内两个流动站可以共视卫星颗数均大于设定的最小阈值（5颗），且卫星的高度角均大于15°为验证其定位精度，将LGO解算的流动站结果作为真值，将PLAOD解算结果与其作差，结果如图1、图2所示。

从图1、图2可以看出利用动态精密单点定位解算的结果大部分历元达到了厘米级结果，极个别的历元超出了1dm的限制。

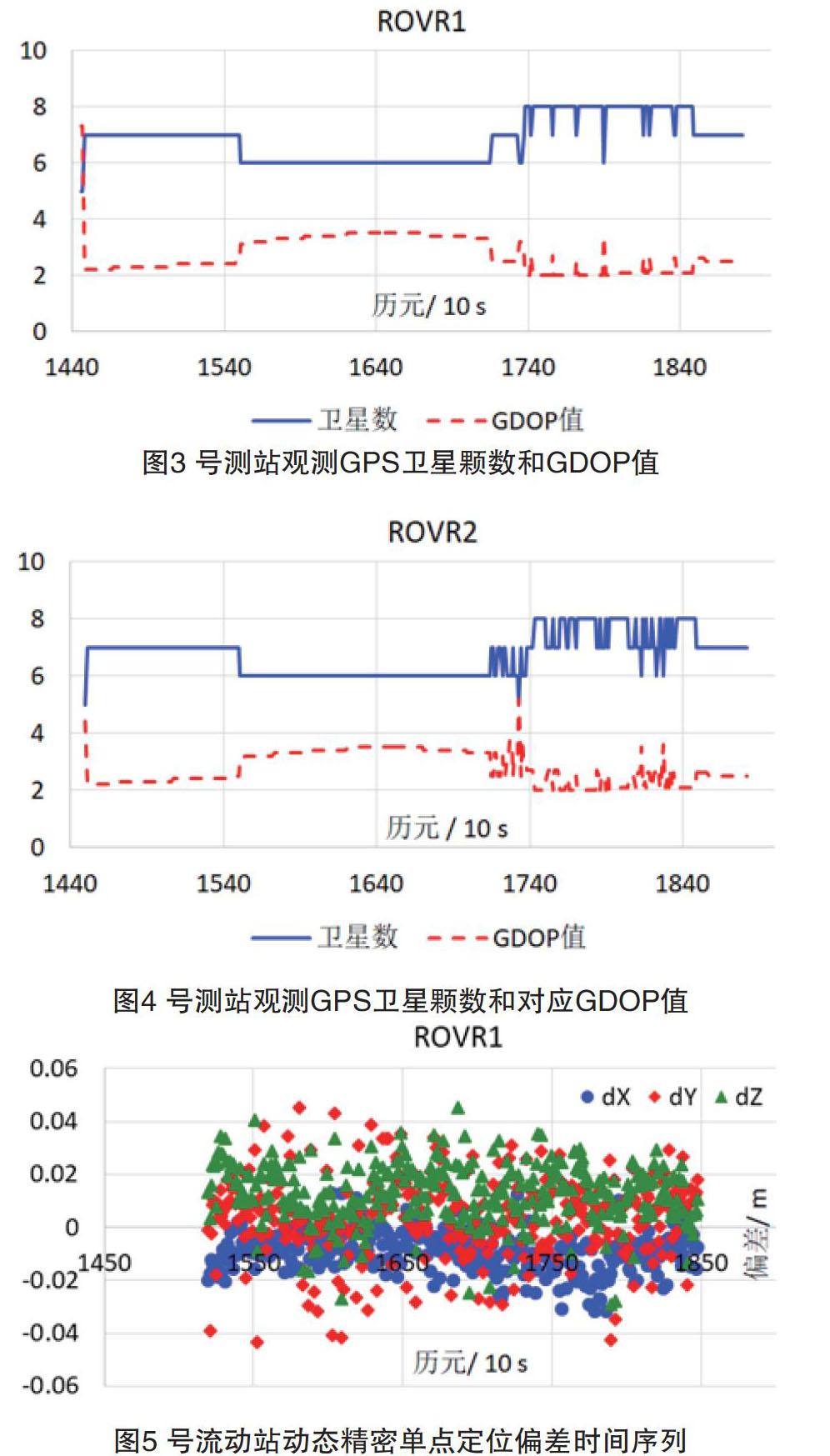
进一步分析其卫星的几何分布和DOP值，如图3和4所示。

从图3、图4可以看出，卫星在接收机静止时锁定的GPS卫星颗数比较稳定，其对应的GDOP值也比较稳定。当接收机处于运动时，其锁定的卫星颗数存在一定的波动，同时对应的GDOP值也波动频繁。卫星发生升降不仅会影响GDOP值，同时会影响模糊度的估计，因为模糊度可能需要重新初始化，重新收敛需要一定的时间。基于这些因素，解算融合GLONASS和GPS观测量的动态精密单点定位结果如图5、图6所示。

从图5、图6图看，加入GLONASS卫星观测量后，定位结果得到了较大的改善，大部分方向偏差均在5cm以内， 2号流动站有极少数历元的方向偏差超过了5cm，但均在1dm以内。融合GPS和GLONASS后的卫星颗数和GDOP值如图7和8所示。

4 结论

通过上述实验分析发现，利用动态精密单点定位技术能获取厘米级的定位准确度，尤其是利用GPS+GLONASS双系统，每个方向上大多能获取±5cm的准确度。通过后续分析发现，平面定位精度较高，而主要偏差则体现在高程方向。这也意味着利用动态精密单点定位在铁路建设行业进行勘测等工作是具备可行性的，同时多星座系统的组合解算，也会对定位精度有很好的提升。

参考文献

[1] 徐绍铨，张华海，杨志强，等.GPS测量原理及应用[M].武汉：武汉大学出版社，2002.

[2] 黄丁发，熊永良，袁林果.全球定位系统（GPS）-理论与实践 [M].成都：西南交通大学出版社，2006.

[3] 张广发.GPS-RTK定位技术在矿山测量中应用及优缺点的探讨[J].西部探矿工程，2014，26（03）：145-146+150.

[4] Zumberge， J. F.， M. B. Heflin， D. C. Jefferson， et al. Precise Point Processing for the Efficient and Robust Analysis of GPS Data from Large Networks[J].J. Geophys. Res.，1997，102（B3）：5005-5017.

[5] Kouba J， Heroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J].GPS Solut，2001，5：12-28.

[6] 韩保民，欧吉坤.基于GPS非差观测值进行精密单點定位研究[J].武汉大学学报（信息科学版），2003，28（4）：409-412.

[7] 任晓东，张柯柯，李星星，等.BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J].测绘学报，2015，44（12）：1307-1313.

[8] Jan Kouba.A Guide To Using International GNSS Service （IGS） Products[EB/OL].（2009-04-23）[2019-01-15].http：//igscb.jpl.nasa.gov/igscb/resource/pubs/usingig-sproductsver21.

[9] Welch G，Bishop G.An Introduction to the Kalman Filter[M].University of North Carolina at Chapel Hill，2001.

[10] Xu Shaoguang， Xiong Yongliang， Liu Ning， et al.  Status and Progress of PLAOD[C].International Symposium on GPS/GNSS 2012，Xian，China.2012-10-31.