基于人工智能的高速动车组轴承剩余寿命预测方法研究

董绪琪 王西山 李彦林

摘 要：轴承是动车组转向架的重要部件之一，其可靠性直接关乎列车运行安全。动车组轴承寿命作为衡量轴承性能的重要指标，主要受材料内因、载荷、润滑液浓度等多重因素影响。为解决动车组轴承剩余寿命预测实效性、准确性问题，本文基于大数据平台进行模型部署，通过神经网络技术进行模型构建，结合轴承温度的相对温升与行驶里程的关系，进行轴承剩余寿命研究方法探究。

关键词：动车组;轴承温升特征;神经网络;轴承剩余寿命

0 引言

轴承作为动车组转向架的重要部件，该工件的好坏直接影响着动车的安全性能和维护成本。经调查美国每年有超过10起与轴承相关的列车故障发生[1]，而我国机车轴承每年有40%需要下车检验，33%需要更换[2]。动车组长期工作在沙漠、高鹽、高海拔、高湿度、多涵洞、永冻土、超载等各种复杂恶劣环境，对轴承的健康状态有着极大的影响，一旦轴承故障，轻则停运救援，重则脱轨。恶劣的环境及高额的故障成本，进一步加剧了轴承寿命预测工作的紧迫性，但实验室通过工况模拟很难做到与现场复杂的工况数据一致;因此，在大数据背景下，应用车载传感器的完整数据，对轴承的剩余寿命进行预测，可有效降低事故率，为轴承从故障修、计划修向预测修、状态修转变提供重要的技术支撑;从而有效提高动车组安全性、降低运维成本。随着大数据、5G等互联网技术逐渐成熟，轴承剩余寿命预测将变得更加智能、精准、高效。

目前，国内外学者对于航空、轿车、风电、精密机床主轴配套轴承等高端轴承都有着广泛而深入的研究，但铁路轴承及其寿命的研究仍然较少。国内动车组运行工况较国外复杂，国内外各大轴承厂商大多根据各自的研究结果及现场经验提出各种轴承寿命的计算方法，针对轴承寿命预测至今没有统一的被行业接受的方法。长期以来大都通过统计分析或振动信号分析开展轴承状态监测，过去的研究主要从力学或故障诊断的观点出发，包括利用力学公式推导或模糊逻辑方法对轴承三维受载、轴承状态和故障模式进行分析，利用统计参数（方根值）、峭度系数或者峰度因子的变化趋势对轴承的缺陷进行建模。或基于国家标准的轴承寿命计算公式基础上，提出不同的修正额定寿命计算方法。现有文献，或是基于载荷进行轴承寿命预测方法[3]，考虑了车辆在低速的情况下载荷等因素对轴承寿命预测，但未对其它（如润滑）影响轴承寿命因素进行考虑。或是通过神经网络进行预测轴承寿命的方法[4]，用加速度传感器测得轴承振动信号，提取振动信号的峭度指标和方均根指标作为特征参数，用神经网络预测轴承未来的振动特征，但没有估计出轴承的剩余寿命。或基于振动退化信号和神经网络的轴承剩余寿命方法[5]，先通过轴承加速寿命试验获得反映轴承性能退化的振动信号，建立轴承退化信号数据库;然后以故障特征频率及其谐波的振幅为特征参数，用神经网络来估计失效寿命。采用相对方均根值研究轴承性能退化规律，利用相关分析选取敏感特征作为输入，构造多变量支持向量机用于轴承剩余寿命预测;然而，由于没有充分考虑轴承处实际运行环境的影响，难以有效的对动车组轴承剩余寿命进行预测。

1 建立反映轴承性能退化的特征指标

根据目前动车组轴承工况复杂、所处环境恶劣等因素，通过构建轴承性能退化指标描述轴承寿命退化特性、应用神经网络技术建立一个泛化度较高的一般轴承寿命预测模型，以完成轴承寿命预测模型构建，技术路线如图1所示。

基于轴承温度监测数据，构建轴承相对温升来描述轴承性能退化特性，有效避免单一工况对轴承剩余寿命预测结果值偏高问题，智能、精准预测轴承剩余寿命，对轴承剩余寿命预测方法的探索性研究具有重要意义。具体步骤如：（1）计算列车累计里程;（2）计算每包数据的里程;（3）计算每行数据累计里程。

筛选一年内，时速大于200km/h的数据，观察轴温工作温度、环境温度、工作温度-环境温度、（工作温度-环境温度）/转速随时间的变化关系;获取轴承温度的相对温升与轴承行驶里程相关性。获取工作温度-环境温度，即轴承温度的相对温升，同列车行驶里程对应关系。其与轴承行驶里程对应关系明显，可作为轴承温升性能退化指标如图2所示。

2 基于性能退化特征构建轴承寿命预测模型

模型构建以动车组轴承全寿命周期内数据为依托，拟合轴承性能退化指标与每万公里行驶里程的对应关系，构建近似工况的轴承性能退化特征与行驶里程的一般性关系模型。应用LSTM预测温差性能退化指标，构建轴承的具体工况与性能退化特征关系模型构建。后期优化基于样本数据逐渐增加、预测与实测差异计算，实现模型模型参数调优、阈值调整，进一步降低轴承故障误报率，轴承剩余寿命预测准确率。

2.1 近似工况下轴承性能退化指标与行驶里程的一般性关系模型

近似工况的轴承性能退化，指的是选取同一条运行线路、同型、同列动车组，相同的制造工艺、相同部位、相同滑条件、相似工作环境等工况的轴承，进行轴承性能退化研究。模型通过拟合轴承性能退化指标与行驶里程的关系，完成轴承性能退化温升特征构建如图3所示。该模型的输入量为轴承的运行里程、输出量为轴承性能退化温升特征。首先，构建单个具体轴承生命周期内性能退化指标随里程的变化;随后运用此方法对近似工况下全生命周期的轴承进行性能退化指标与里程关系拟合;最后根据轴承拟合结果，创建泛化能力较高的趋于一般轴承的特征曲线簇。

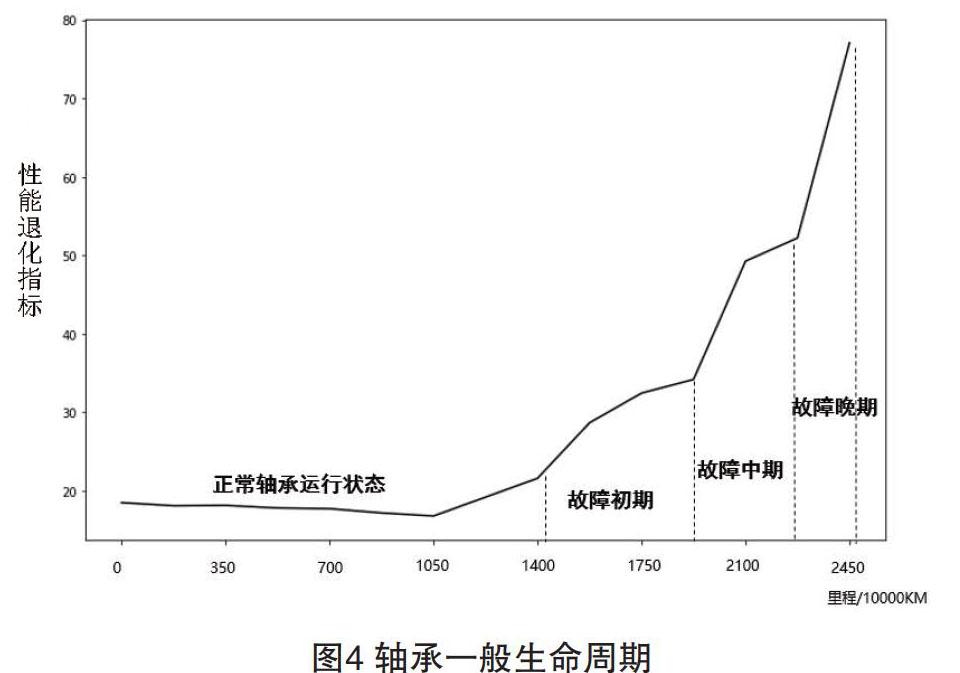
轴承全生命周期，可通过故障的发生、发展程度，构造故障标识量、性能退化指标进行数量化表征。通常故障的发生一般由一些细微有害因素不断累积扩大或次生危害性因素的产生与累加，最终使得零部件或系统的性能不能满足设计要求，从而表现为失效或故障。即，其轴承全生命周期运行可分为四种时态为正常轴承运行状态、故障萌生和初步发展的故障初期、故障进一步发展的故障中期、故障持续恶化导致最终失效的故障晚期如图4所示。

2.2 轴承的具体工况与性能退化特征关系模型构建

DNN作為全连接的神经元结构，目前运用于国内外多个神经网络预测模型，取得了不错的效果，可惜这些模型仍需较多的轴承试验来保证预测精度。因无过多的轴承来确保试验的准确性，故其试验结果缺乏相关实际根据。原始的RNN无法记住长期信息，而LSTM（长短记忆神经网络），细胞状态直接在整个链上运行，只有一些少量通过“门”进行线性交互，信息在上面流传保持不变变得容易，保证了信息长期记忆。从而使动车组轴承通过变化的时间序列预测轴承性能退化指标成为了可能。

通过应用LSTM算法预测轴承性能退化指标，构建轴承的具体工况与性能退化特征关系模型，获取预测轴承性能退化指标输出;以实现轴承特定工况下，未来某个时刻轴承的性能退化轴承性能退化指标的预测。该模型的输入量为某轴承最近5小时工况数据，输出量为未来轴承性能退化指标，进行未来某时刻轴承性能退化指标的预测。

最终，将预测的未来轴承性能退化指标代入近似工况的轴承性能退化特征与行驶里程的一般性关系模型，完成轴承剩余寿命预测模型的构建，该模型的输入量为某轴承最近工况数据，输出量为轴承的剩余运行里程。

3 剩余寿命预测模型验证与应用

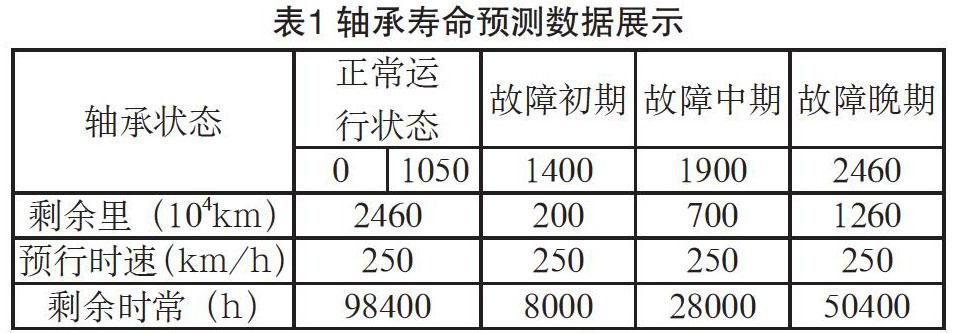
为检测具体工况下轴承剩余寿命模型的一般泛化能力和应用效果。以CR400AFXXXX动车组为例，通过输入当前时间点对应的运行时间、里程、时速等轴承的工况数据如表1所示。

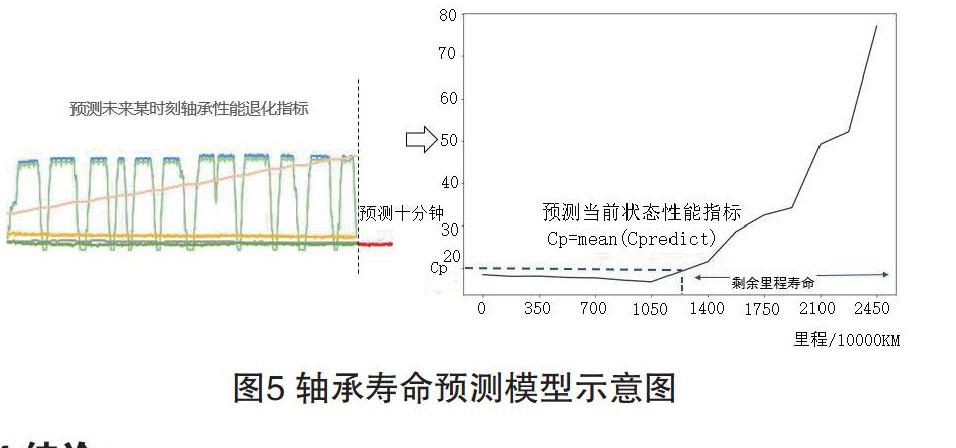
结果表明，该轴承已进入故障初期，将于50400h后彻底失效。并将预测结果存入检测中心轴承监测数据库，经后期维护数据与预测数据对比，得知该模型误差为1.24%，能够达到轴承寿命预测预期目标。轴承寿命预测模型示意图如图5所示。

4 结论

本文以解决动车组实际工况环境下轴承剩余寿命预测为主旨，以动车组轴承实际工况下运行数据为依托，完成基于大数据的高速动车组轴承剩余寿命预测方法研究。后期经大量轴承真实数据进行分析、拟合与验证模型，最终形成研究结论如下：

（1）提出了基于温度的轴承性能退化指标构造方法。本实验采用动车组实际运行全生命周期数据进行试验;综合考量轴承性能退化影响因素后，通过轴承性能退化机理及算法拟合轴承温度、轴承温度-环境温度、（轴承温度-环境温度）/转速与轴承运行时间确立的;该指标结合了轴承工况下的多重因素，且对早期故障敏感，为剩余寿命预测奠定了基础。（2）形成了基于温度的性能退化指标的轴承寿命预测方法。本模型基于大量动车组全生命周期内的轴承运行数据，完整的反应同类轴承的性能预测，相较其他在实验室中的模型能够更真实的展示轴承剩余寿命信息;通过长短记忆神经网络精准地预测未来某时刻温差性能退化指标，实现对轴承剩余寿命预测。（3）提出了一种全新的轴承故障概率计算方法。该方法基于LSTM温差性能退化指标，通过将预测温差性能退化指标与里程对应面积与全生命周期轴承性能退化指标与里程面积进行求比值即可得到轴承的全生命周期中不同阶段的故障概率。

参考文献

[1] Sneed W H，Smith R L.On-board real-time railroad bearing defect detection and Monitoring[C].Railroad Conference，American，April 15-16，1998：149-153.

[2] 李兴林.滚动轴承故障监测诊断技术应用进展[J].工程与试验，2009（4）：1-5.

[3] 刘德昆，李强，王曦，等.动车组轴箱轴承基于实测载荷的寿命预测方法[J].机械工程学报，2016（22）：45-54.

[4] Shao， Y; Nezu， K. Prognosis of Remaining Bearing Life using Neural Networks[J].Proceedings of the Institution of Mechanical Engineers-Part I，2000，214（3）：217.

[5] GEBRAEEL N， LAWLEY M， LIU R.Residual life， predictions from vibra- tion-based degradation signals：a neural network approach[J].IEEE Tran-sactions on Industrial Electronics，2004，51（3）：694-700.