孔洞对3D打印AlSi10Mg合金拉伸性能影响的分子动力学模拟

陈传波 马芳 罗一平

摘要：采用分子动力学方法模拟含孔洞的3D打印AlSi10Mg合金单轴拉伸过程，研究孔洞对晶体力学行为影响。结果表明：随着孔洞尺寸的增加，材料的弹性模量、屈服强度、峰值应变都相应下降。孔洞数量的增加，加剧了拉伸断裂进程。本研究主要从原子尺度分析孔洞对多元合金力学性能影响，为今后实验和研究孔洞对3D打印提供理论指导。

关键词： AlSi10Mg合金; 单轴拉伸; 孔洞; 分子动力学模拟

【Abstract】 The uniaxial stretching process of 3D printed AlSi10Mg alloy with voids is simulated by molecular dynamics method， and the influence of pores on the mechanical behavior of the crystal is studied. The results show that the elastic modulus， yield strength and peak strain of the material decrease with the increase of the pore size. The increase in the number of holes exacerbates the tensile fracture process. This study mainly analyzes the influence of pores on the mechanical properties of multi-alloys at the atomic scale， and provides theoretical guidance for future experiments and research on holes for 3D printing.

【Key words】  AlSi10Mg alloy; uniaxial tension; holes; molecular dynamics simulation

0 引 言

随着汽车行业的不断发展，对环境、能源和交通安全等方面产生了很大影响。汽车轻量化作为现在研究的热门课题，吸引了大批科研人员从事轻量化材料研究，而铝合金[1]是轻质材料的代表，具有较高的强度和硬度。而3D打印技术是可以根据不同设计需求，层层堆垛的新型成形制造技术。AlSi10Mg作为3D打印的一种十分普遍的材料，被众多学者广泛研究。柯宇等人[2]对选区激光熔化的AlSi10Mg合金进行了微观组织分析和力学性能研究，发现经过时效处理后，硬度有所降低。李保强等人[3]对AlSi10Mg合金进行了有限元模拟，得出熔池搭接区域残余应力高，中间偏低。万华亮等人[4]对3D打印AlSi10Mg合金的孔洞进行了分析，预估了孔隙率对增材制造疲劳寿命影响。

目前，对AlSi10Mg合金的研究大多是物理实验及微观尺度的热应力模拟，对原子层面的拉伸力学性能的研究却不是很多，且基本集中在单质金属元素的拉伸模拟。刘明辉等人[5]研究了铝合金刃型位错与合金元素的相互作用，从原子层面解释了位错钉扎对铝合金的强化作用。张宁等人[6]研究球形孔洞对双晶铜单向拉伸的影响，得出孔洞显著降低了双晶体的弹性模量和屈服应力。梁华等人[7]研究了孔洞和空位对铝单晶力学性能的影响，得出不同晶向的拉伸，孔洞的生长变形微观机制不同。阐明了形变机制主要是位错的移动、堆积和发射。

本文主要对含孔洞AlSi10Mg合金进行拉伸模拟，分析孔洞大小对其力学性能的影响，为3D打印AlSi10Mg合金缺陷引起的破坏机理提供依据。

1 计算模型与方法

1.1 模型建立

3D打印AlSi10Mg合金主要过程是通过高能激光熔化AlSi10Mg金属粉末，冷却凝固得到相应制品，但由于物理实验限制，必然会产生孔洞。使用分子动力学方法，模拟其制备过程：首先，建立晶格常数为a0=b0=c0=4.045 27 ，α=β=γ=90°的面心立方（fcc）的Al单晶;然后，通过Si和Mg以质量分数为0.10及0.05替换Al原子，生成AlSi10Mg合金，并使用共轭梯度法进行能量最小化弛豫;最后，建立晶胞大小为15a0×15a0×15a0的拉伸模型，AlSi10Mg合金体系即如图1所示。笛卡尔坐标系x， y， z轴分别对应晶体的[100]、[010]、[001]晶向。模拟过程中，体系采用了周期性边界。

1.2 工况设计

由于体系属于纳米尺度的下拉伸模型，使得应变率比实验中高出几个数量级[8]。本文采用的应变率为2×109/s。工况一：孔洞尺寸分别为1a0， 3a0和5a0。工况二：孔洞个数有1，2，4个，尺寸为2a0，孔洞沿z轴方向，位置分布为中心对称。

从图2可以得出，在不同孔洞尺寸和不同孔洞个数情况下，AlSi10Mg合金的拉伸应力-应变曲线的变化趋势都大致相似，可以将其分为3个阶段。

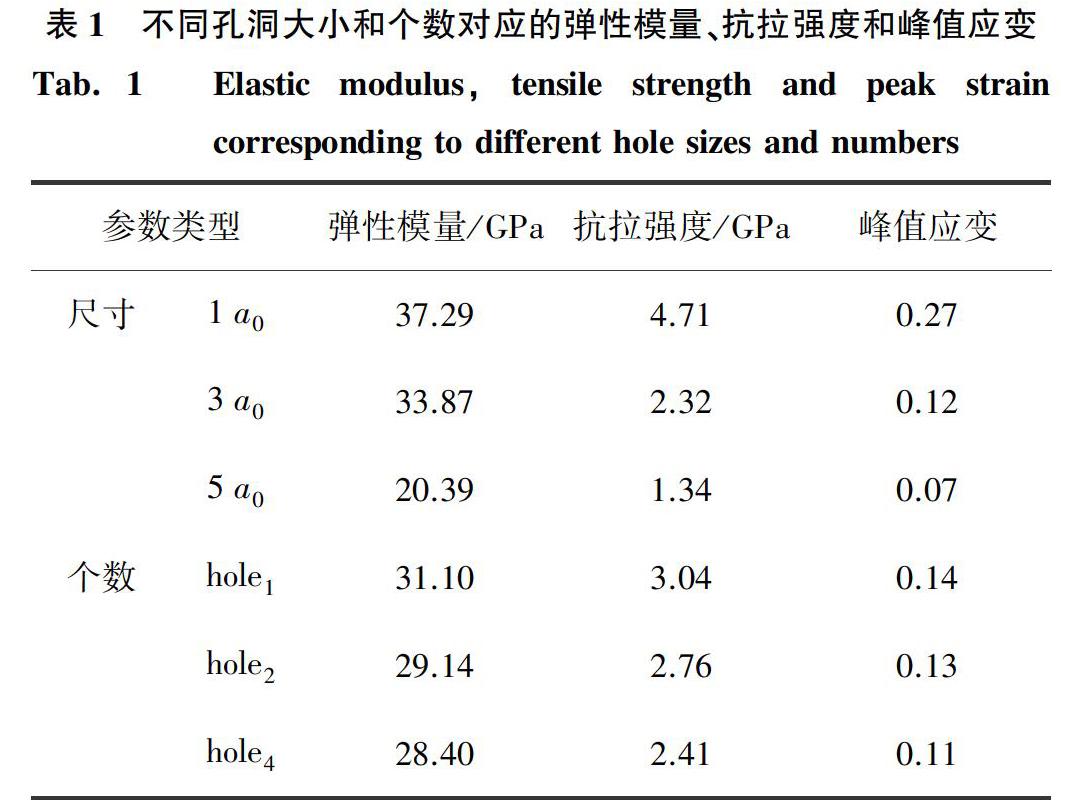
第一阶段是弹性阶段，动态拉伸的应力-应变曲线呈线性关系;第二阶段是屈服阶段，应力-应变同曲线呈非线性关系，产生塑性变形;第三阶段是断裂阶段，应力随着应变增加而减小，直至发生断裂。AlSi10Mg合金力学性能参数见表1。

从图2及表1可以看出，随着孔洞大小从1a0升高到5a0，AlSi10Mg弹性模量从37.29 GPa减小到20.39 GPa，抗拉强度从4.71 GPa降低到1.34 GPa，峰值应变从0.27減少到0.07;孔洞个数从1个增加到4个，弹性模量从31.10 GPa减小到28.40 GPa，抗拉强度从3.04 GPa降低到2.41 GPa，峰值应变从0.14减少到0.11。

2.2 原子结构演化

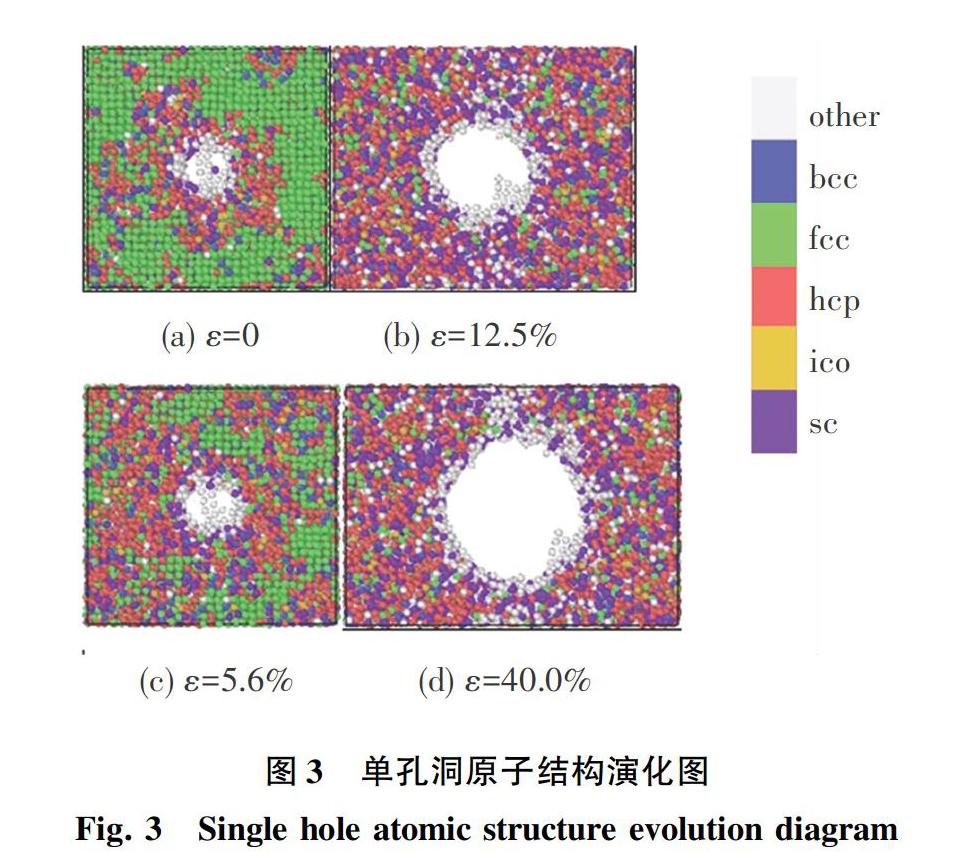
为了进一步研究孔洞对拉伸性能的影响，从原子组织演变角度来进行探究，采用OVITO软件对AlSi10Mg合金体系进行PTM分析。图3和图4分别是含有1个孔洞和2个孔洞动态拉伸图，孔洞尺寸皆为2a0，应变率为2×109/s。其中，灰白色、蓝色、绿色和红色分别代表other（无序）、bcc（体心立方）、fcc（面心立方）、hcp（密排六方）、ico（二十面体协调）和sc（简单立方）原子结构。

从图2的动态拉伸应力-应变曲线可知，当单孔AlSi10Mg合金体系应变为5.6%、12.5%及40.0%时，分别处于拉伸过程中的弹性形变阶段、屈服形变阶段和断裂形变阶段。从图3可以观察到，單孔AlSi10Mg合金在弹性应变阶段，fcc结构占主体;从弹性形变到屈服形变阶段，原子结构从fcc向hcp转变;随着应变的增加，孔洞逐渐增大，周围无序原子增多，hcp和sc结构原子占大多数，直到拉伸断裂。

图4相较于图3，孔洞增加了1个，在弹性变形阶段，hcp结构和fcc结构占比接近;随着应变的增加，fcc结构逐渐减少，hcp结构和sc结构不断增加。孔洞周围的无序原子增多，且2个孔洞增长基本一致。

3 结束语

本文运用分子动力学模拟了含孔洞的AlSi10Mg合金体系的单轴动态拉伸过程，对合金拉伸形变过程进行了研究。结果表明：

（1）随着孔洞大小从1a0升高到5a0，AlSi10Mg弹性模量从37.29 GPa减小到20.39 GPa，抗拉强度从4.71 GPa降低到1.34 GPa，峰值应变从0.27减少到0.07;孔洞个数从1个增加到4个，弹性模量从31.10 GPa减小到28.40 GPa，抗拉强度从3.04 GPa降低到2.41 GPa，峰值应变从0.14减少到0.11。

（2） 随着拉伸应变的增加，fcc结构逐渐减少，hcp和sc结构明显增多，孔洞周围的无序原子伴随着孔洞的增长而增多。

参考文献

[1] LI Hui， YAN Zhaohui， CAO Lingyong. Bake hardening behavior and precipitation kinetic of a novel Al-Mg-Si-Cu aluminum alloy for lightweight automotive body[J]. Materials Science & Engineering A， 2018， 728：88.

[2] 柯宇， 马盼， 马永超，等. 激光选区熔化AlSi10Mg合金微观组织及力学性能研究[J]. 应用激光， 2019， 39（2）：198.[JY]（下转第361页）

[FL）]

[3] 李保强， 李忠华， 白培康，等. 选区激光熔化AlSi10Mg应力场数值模拟研究[J]. 应用激光， 2019（2）：211.

[4] 万华亮， 王奇志. 增材制造铝镁合金AlSi10Mg的疲劳性能研究[J]. 强度与环境， 2019（3）：20.

[5] 刘明辉， 肖伟， 王建伟，等. 铝合金中刃型位错与合金元素相互作用的分子动力学模拟研究[J]. 稀有金属， 2017，41（3）：233.

[6] 张宁， 杨新华， 陈传尧. 含球形孔洞双晶铜单向拉伸性能的分子动力学模拟[J]. 计算力学学报， 2010（2）：330.

[7] 梁华， 李茂生. 孔洞和空位对单晶铝力学性能影响的分子动力学研究[J]. 计算物理， 2019， 36（2）：211.

[8] 周继凯， 朱清华. Fe-C合金动态拉伸力学性能温度和应变率效应分子动力学[J]. 科学技术与工程， 2019， 19（11）：61.

[9] JELINEK B ， GROH S ， HORSTEMEYER M F ， et al. MEAM potentials for the Al， Si， Mg， Cu， and Fe alloys[J]. Physical Review B， 2012， 85（24）：245102.

[10]LARSEN P M， SCHMIDT S， SCHIφTZ J . Robust structural identification via polyhedral template matching[J]. Modelling and Simulation in Materials Science and Engineering， 2016， 24（5）：055007.