一类带奇异项的Schrödinger-Poisson系统正解的唯一性
侯艾君,蒲 洋,廖家锋,2*
(1.西华师范大学数学与信息学院,四川南充637002; 2.西华师范大学公共数学学院,四川南充637002)
1 前言及主要结论
考虑如下带奇异项的 Schrödinger-Poisson系统
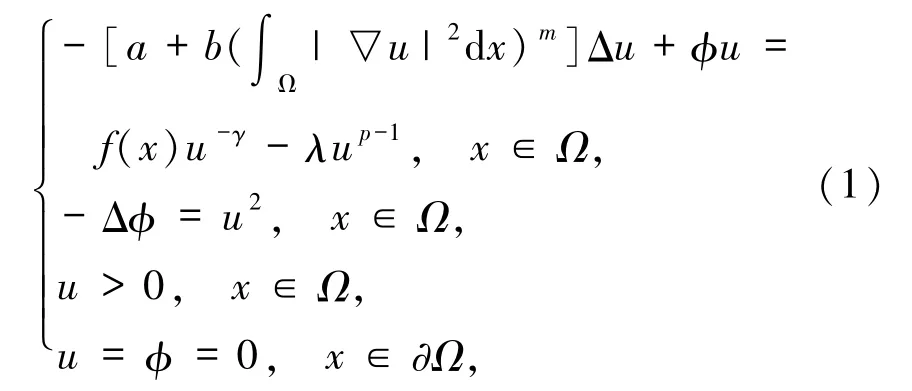
其中,Ω⊂R3是一个有界开区域且具有光滑边界∂Ω,a,b≥0且a+b > 0,m > 0,λ ≥0,1 < p≤6,0< γ < 1为非零非负函数.6为Sobolev空间嵌入到Lp(Ω)(p∈[1,6])的临界Sobolev指数.是Kirchhoff型非局部项,故当 b>0时,系统(1)又称为奇异的Kirchhoff-Schrödinger-Poisson 系统.记
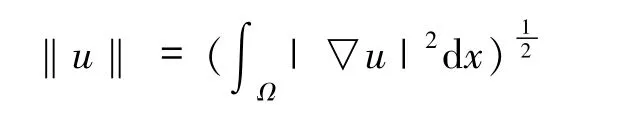
和
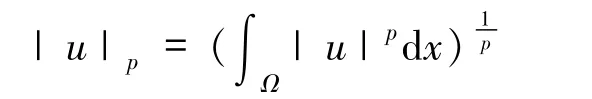
当a=1,b=λ =0时,文献[1]研究了系统(1),即
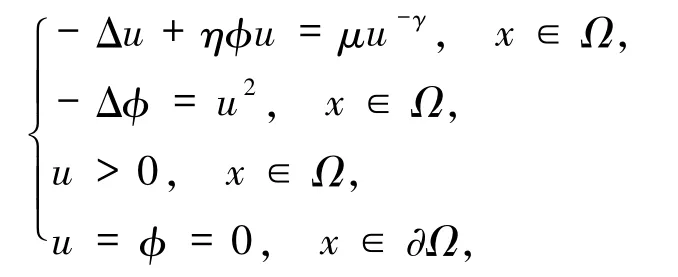
其中,η=±1,μ>0.利用变分方法,当 η=1时,获得了系统正解的存在唯一性;当η=-1且μ>0充分小时,获得了系统2个正解的存在性.文献[2]研究 Kirchhoff-Schrödinger-Poisson 系统
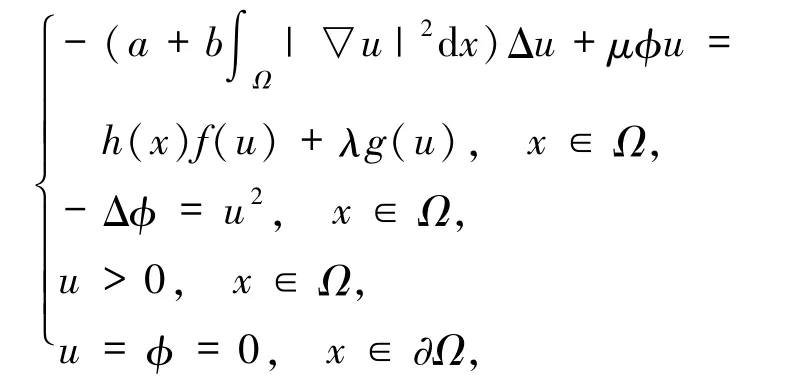
其中,Ω⊂R3是一个有界开区域且具有光滑边界∂Ω,a,b≥0 且 a+b>0,λ,μ∈R+=[0,+ ∞),f∈C((0,+∞),R+)在 0 附近非增且有(即具有奇异性),g∈C(R+,R+),系数函数h为满足一定条件的正函数,当f、g满足一定的条件时,获得该系统正解的存在性和唯一性.此外,文献[3]还获得了带一般奇异项的 Kirchhoff-Schrödinger-Poisson系统的2个正解.其它有界区域上的 Schrödinger-Poisson系统的可参见文献[4-6].文献[7-9]研究了系统(1)中单个方程的非局部问题.文献[10-15]等对奇异Kirchhoff型问题进行了广泛研究.
一个自然的问题:系统(1)是否也存在正解?本文利用变分方法和临界点理论,证得系统(1)正解的存在唯一性,从而推广了文献[1]中定理1.1的结果.具体结论如下.
定理1假设 a,b≥0 且为非零非负函数,系统(1)都存在唯一的正解
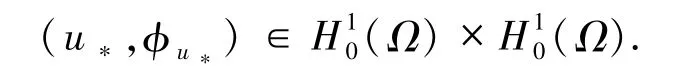
注1一方面,定理1将文献[1]的部分结果推广至奇异的Kirchhoff-Schrödinger-Poisson系统;另一方面,文献[2]只对具有非局部项的奇异的Kirchhoff-Schrödinger-Poisson系统进行了研究.定理1将文献[2]的部分结果推广到具有的奇异的 Kirchhoff-Schrödinger-Poisson 系统.
2 定理的证明
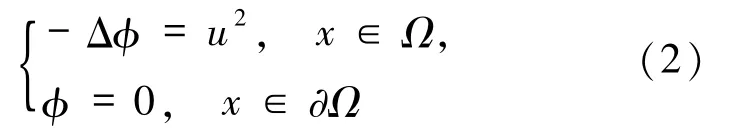
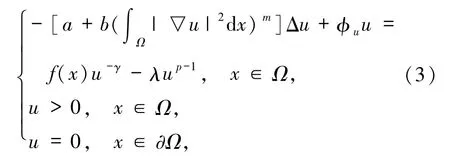
从而,系统(1)的解就等价于求问题(3)的解.
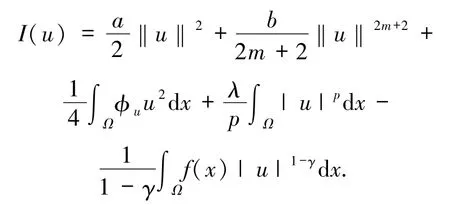
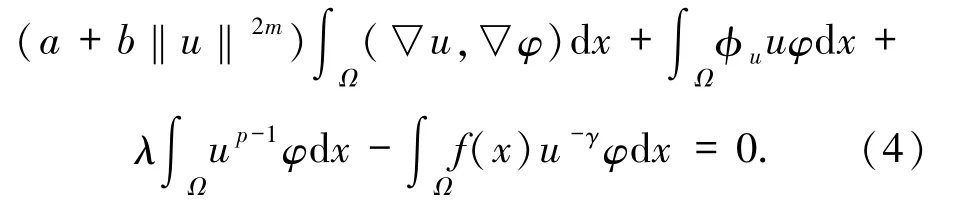
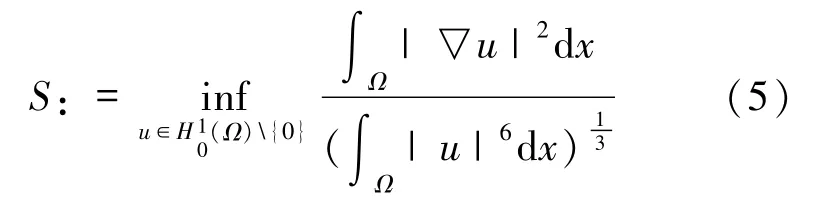
的最佳Sobolev常数.
首先,为了方便,根据文献[1]的引理2.1,给出问题(2)解φu的如下重要性质.
命题1[1]1);
2)φu≥0,且当 u>0时,有 φu>0;
3)对任意的 t∈R 且 t≠0,有 φtu=t2φu;
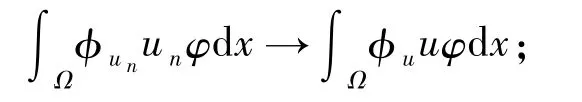
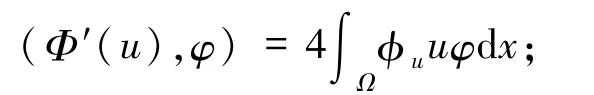
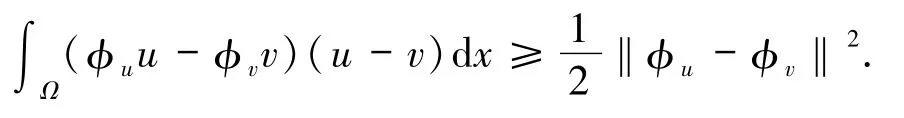
引理1假设 a,b≥0且为非零非负函数,则泛函 I在能达到极小值,即存在 u*∈,使得
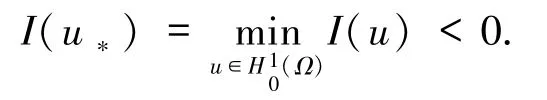
证明不妨记首先,证明m*是有定义的.由Hölder不等式和(5)式得
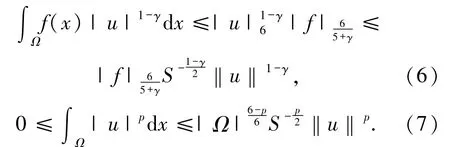
根据命题1中的性质2)以及(6)和(7)式可得
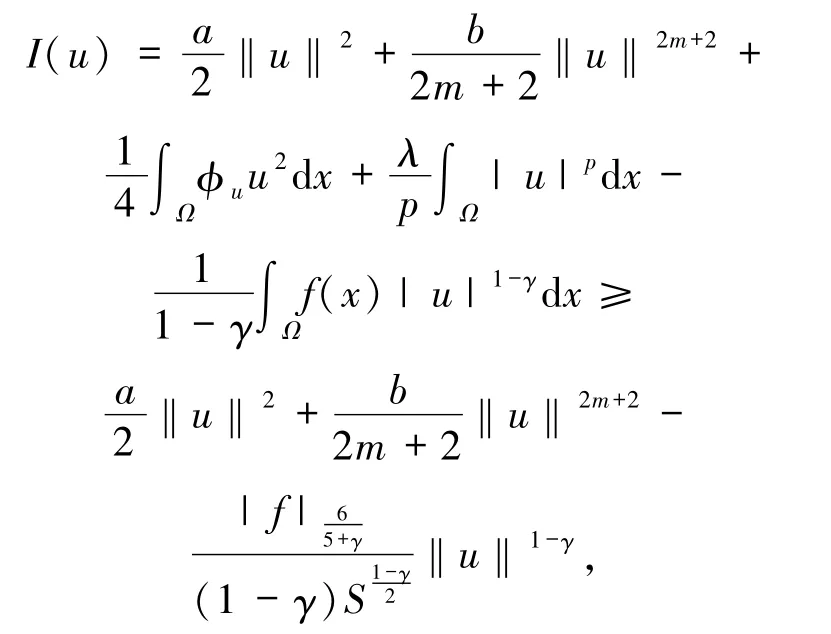
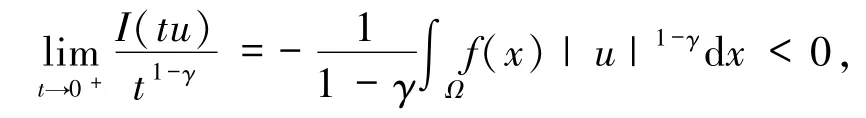
这就意味着:m*<0.接下来,证明在空间中m*是可达的.
根据m*的定义,存在一个极小化序列使得由 I(|un|)=I(un),不妨假设 un≥0在 Ω 中几乎处处成立.显然,{un}在中有界.从而存在一个子列(仍记为{un})和u*≥0使得当n→∞时,有

令wn=un-u*,只需证明当n→∞时‖wn‖→0.根据文献[12]中的(6)式,可得
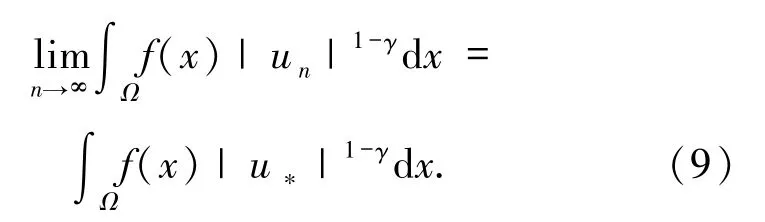
进一步,由(8)式和 Brézis-Lieb 引理可得
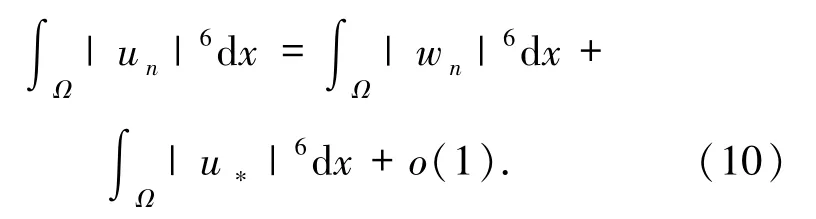
一方面,1<p<6时,依据(8)、(9)式和命题1 中的性质5)以及范数的弱下半连续性,可得
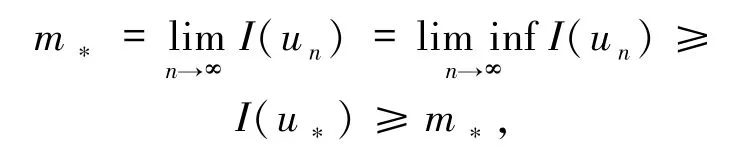
这就意味着I(u*)=m*.另一方面,p=6时,依据(8)~(10)式和命题1中的性质5)以及范数的弱下半连续性,可得
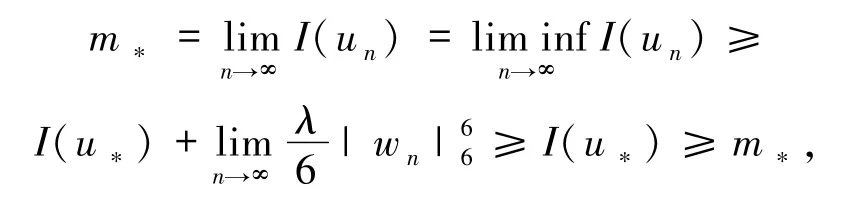
这就得到I(u*)=m*.引理1证毕.
接下来给出定理1的证明.
定理1的证明事实上,只需证明为问题(3)的解,即是系统(1)的解.
首先,证明u*(x)>0在Ω中几乎处处成立.由,有
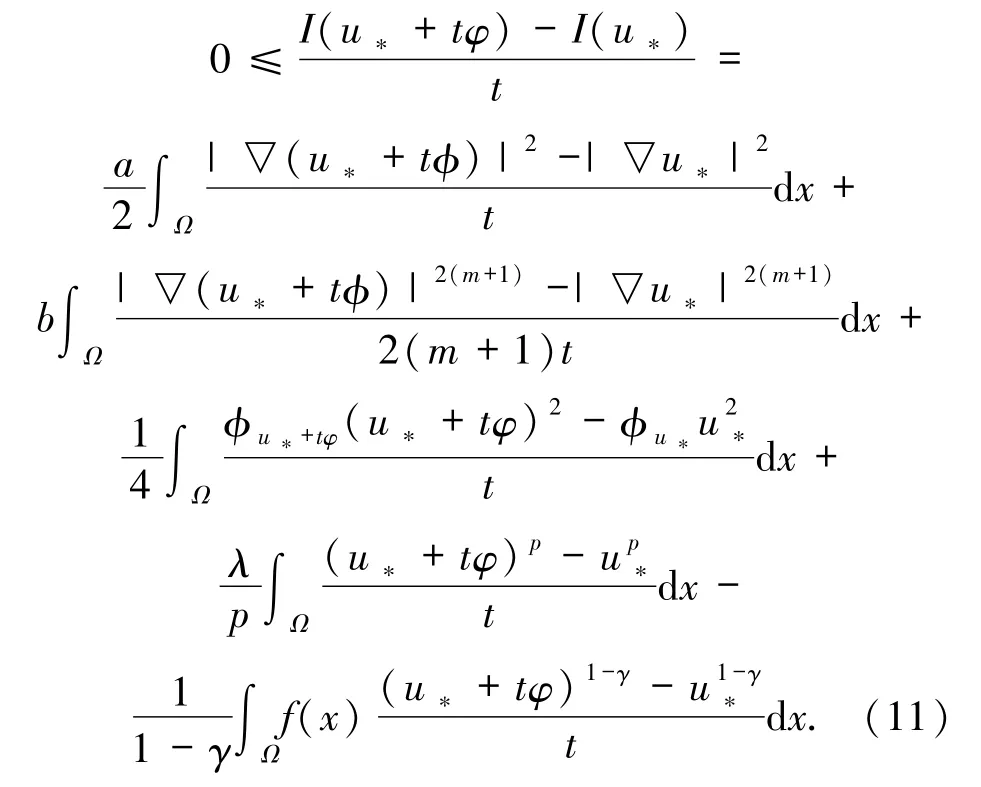
根据Lebesgue控制收敛定理,可得
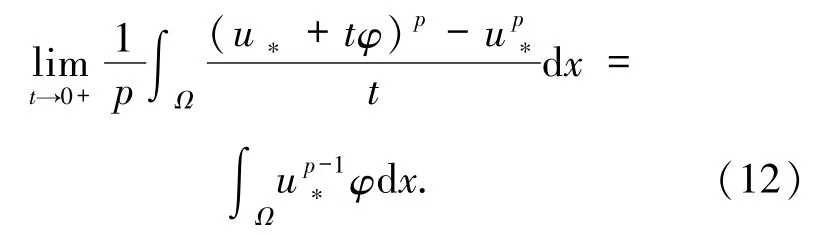
对任意的x∈Ω,记
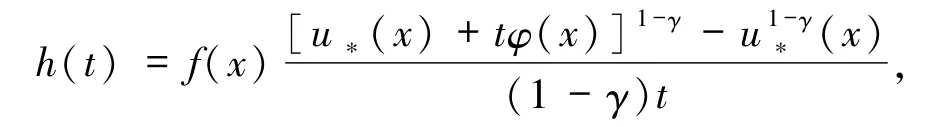
则
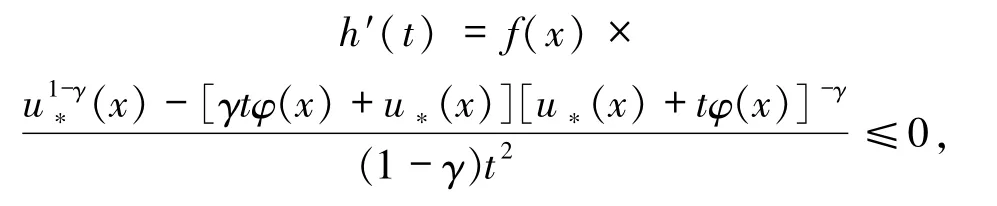
这就意味着:h(t)对一切的t>0是非增的.进一步,对任意的x∈Ω,有,其中,当 u*(x)=0且 φ(x)>0时,上式值可能是+∞.从而,根据单调收敛定理(Beppo-Levi定理),可得
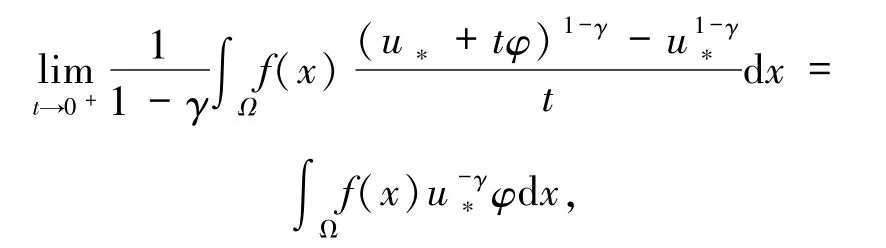
这里可能取到+∞.再结合(12)式和命题1中的性质 6),在(11)式中让 t→0+,可得
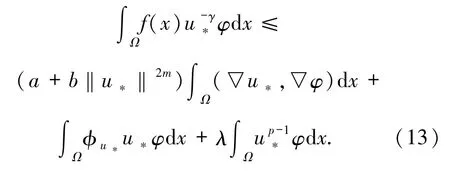
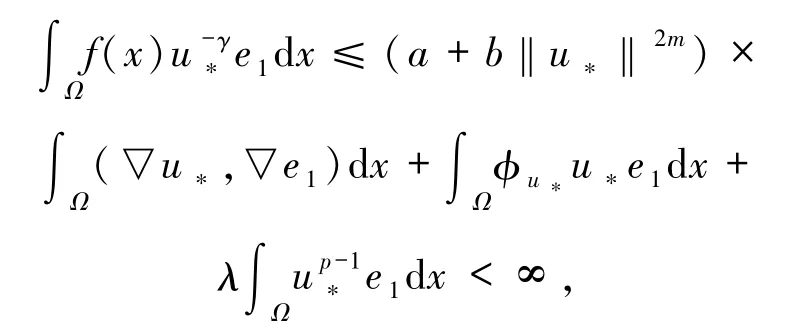
这就意味着u*(x)>0在Ω中几乎处处成立.
接下来,证明u*是问题(3)的解.即只需证明u*满足(4)式.根据(13)式,只需证明(13)式对一切的都成立.定义η:[-δ,δ]→R 为η(t):=I(u*+tu*),则 η 在 t=0 处达到极小值,这就意味着
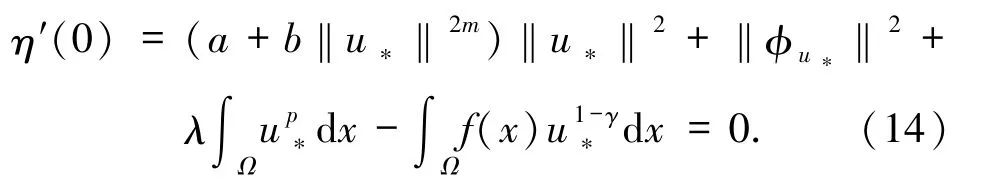
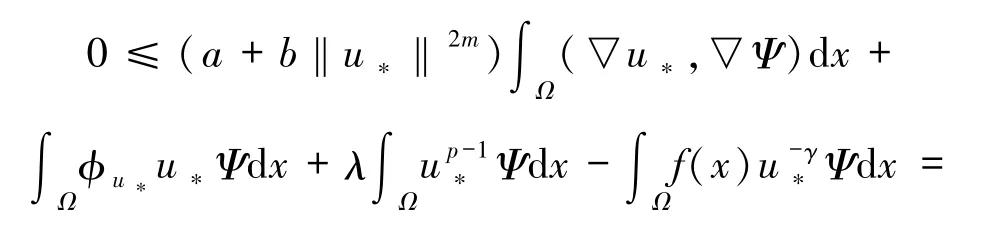
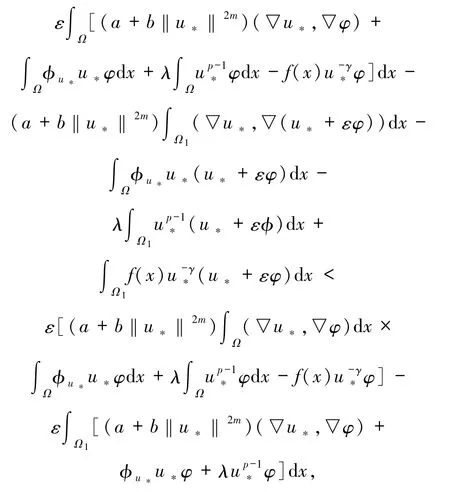
当 ε→0+,有 meas Ω1→0,上式两边同时除以 ε,并令 ε→0+,可推得
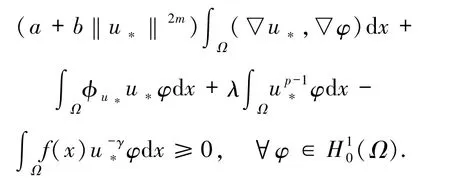
因此,这个不等式对于-φ也成立,故u*是问题(3)的一个正解,且 I(u*)<0.因此,(u*,φu*)是系统(1)的解.
最后,证系统(1)解的唯一性.即证明问题(3)解的唯一性.假设v*为问题(3)的另一个解.由(4)式可得
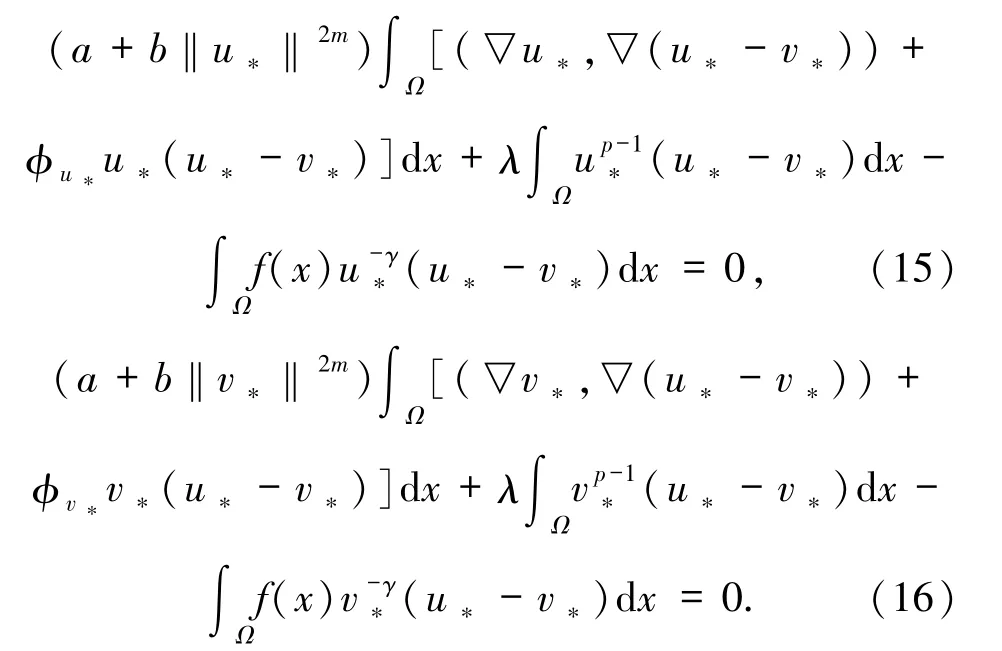
根据(15)和(16)式可得
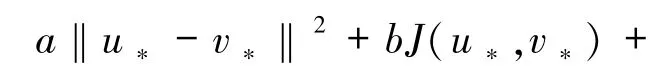
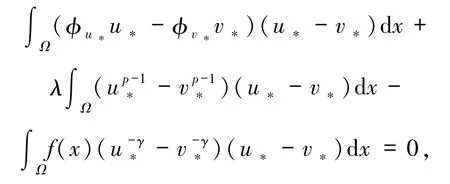
其中
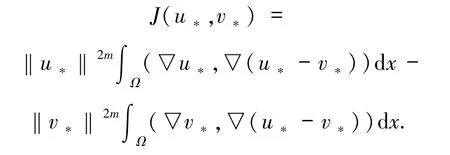
根据Hölder不等式,可得
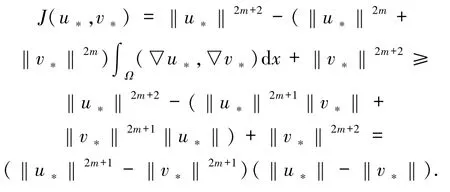
由0<γ<1,p>1,容易得到
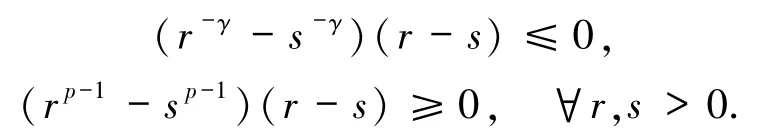
因此
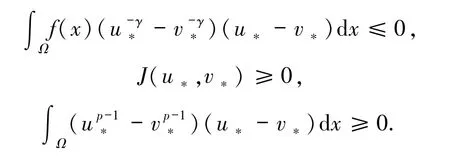
一方面,若 a>0,再结合命题1中的性质8),由(17)式得到 a‖u*-v*‖2≤0.这就意味着‖u*-v*‖2=0,即u*=v*.另一方面,若 a=0,再结合命题1中的性质 8),由(17)式可得‖u*‖ =‖v*‖,且 J(u*,v*)=0.从而有
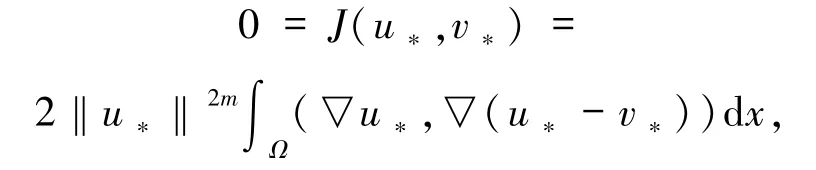
即 u*=v*.因此,(u*,φu*)是系统(1)的唯一解.定理1证毕.
致谢西华师范大学基本科研基金项目(15D006和16E014)和西华师范大学创新团队科研基金项目(CXTD2018-8)对本文给予了资助,谨致谢意.

