n阶α次积分C半群扰动的一个结果

周裕然， 赵华新， 周 阳

（延安大学 数学与计算机科学学院，陕西延安 716000）

算子半群的扰动理论是算子半群的重要内容之一，许多学者对此作了大量的研究工作. 文献［1-4］研究了C 半群的解析性、扰动及扰动C 半群的紧性等相关性质. 文献［5-6］讨论了双参数C 半群的指数公式、谱及其扰动. 文献［7-8］讨论了扰动双参数C 半群与双参数有界算子C 群. 文献［9-11］讨论了n 次积分C 半群扰动的相关定理. 文献［12-14］讨论了α 次积分C 半群扰动的相关定理. 宋晓秋、张明翠［15-16］给出了n 阶α 次积分C 半群的概念、预解集以及次生成元等，并研究了相关问题.

1 预备知识

在本文中，X 为无限维的复Banach空间，B( X )是X 上有界线性算子全体所成的Banach代数；D( A) 为线性算子A 的定义域，设n ∈N，α ≥0.

T=0 当且仅当存在n ≥0 使JnT( t )=0，t ≥0.

2 基本概念和引理

定义1［15］设n ∈N，α ≥0，C ∈B( X )是单射，{T ( t)}t≥0⊂B( X )强连续. 若存在闭线性算子A 使（1）、（2）式成立或（1）、（3）式成立，

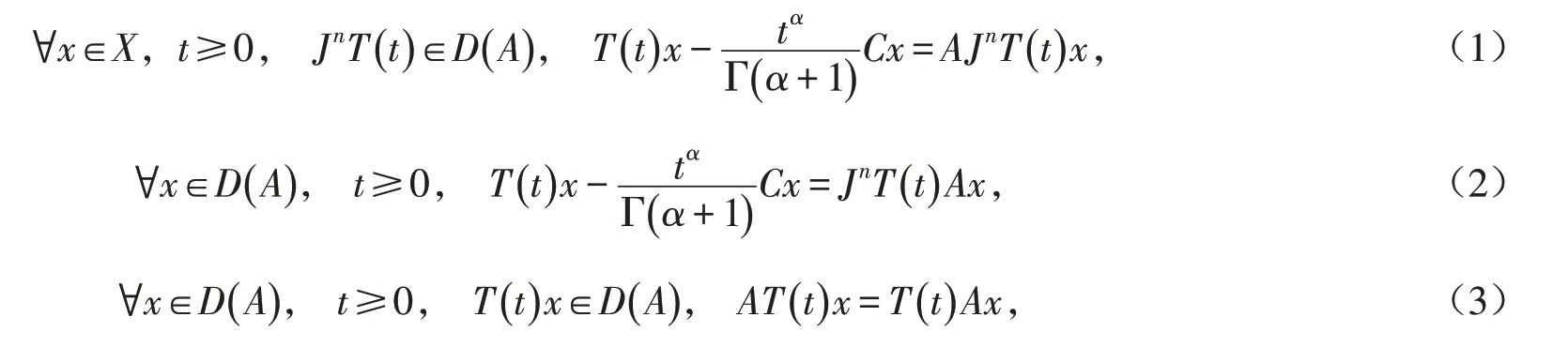
3 主要结果

证明

由预解方程可得：

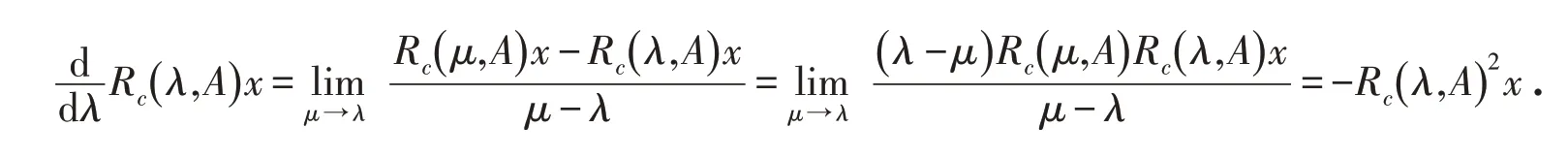
利用数学归纳法可证

定理得证.

rA 生成一个n 阶α 次积分CB半群.