养殖水质氨氮混合软测量模型研究
林少涵,王 魏,2,王奕鹏
(1 大连海洋大学信息工程学院,辽宁 大连116023;2 教育部设施渔业重点实验室,辽宁 大连116023)
目前,中国集约化水产养殖对养殖水质和水体环境的实时监测水平较低,缺乏系统的水产疾病预警技术。根据渔业水质标准的规定,安全的氨氮质量浓度应保持在0.2 mg/L以下[1],过高的氨氮会严重影响到水生生物的生存,甚至引起死亡,对养殖造成巨大经济损失。因此,对氨氮的检测是有效预防氨氮毒害事件发生的必要措施。目前,大部分氨氮检测仪价格昂贵且不适用于测量海水。国内对氨氮检测的主要方法有纳氏试剂比色法、电极法、次溴酸盐氧化法等[2]。这些检测方法虽然能够有效地对氨氮质量浓度进行检测,但都属于离线方法,难以实现实时检测。近年来,随着软测量技术的发展,国内很多知名专家学者开始将软测量技术应用到氨氮检测领域。软测量是指通过计算机技术构造某种数学关系,利用一些较易获得的变量来估计生产过程中难以测量的重要变量。Deng等[3]提出基于RBF的在线软测量方法。在污水处理方面,乔俊飞等[4]提出基于递归RBF神经网络的氨氮预测模型,使用梯度下降法训练模型参数,并对氨氮质量浓度进行预测,虽然有较高的精度,但是仍然存在模型结构复杂、泛化能力差的问题。卢超等[5]提出一种基于尖峰自组织径向基神经网络的氨氮检测方法,该方法的创新之处在于能够根据输入信息实时更新网络参数,并通过尖峰自组织机制调整网络结构,提高氨氮的预测精度和自适应力,但也存在模型结构参数在动态优化上的不足。在养殖水体的氨氮检测方面,陈英义等[6]提出了基于改进深度信念网络的氨氮预测模型,利用自学习方法确定网络结构,通过PSO算法找出最优的结构参数,达到提高模型精度的目的,但同时仍存在网络结构参数不易确定等问题。这些都是神经网络在氨氮测定上的应用。然而,训练高精度的神经网络模型需要大量的数据样本,在实际应用中要获得大量有标签的样本较为不易,而且由于神经网络的“黑箱”特性,建立的模型不具备解释能力。
采用广义可加模型进行氨氮预测,该方法对于小样本数据能够快速建立有较好精度的模型,且建立的模型有一定的解释能力。为了提高预测精度,采用同样适用于小样本数据的支持向量回归对广义可加模型的输出进行误差补偿。
1 氨氮质量浓度软测量建模策略
1.1 循环水养殖工艺过程描述
循环水养殖系统利用生物反应、物理过滤等方法,去除养殖水体中所含的废物残渣、亚硝酸盐氮、氨氮化合物等有害物。其组成部分主要包括:生化反应系统、消毒杀菌系统、过滤系统和智能监控系统。智能监控系统是科学养殖的一个关键环节,主要作用是监控水体的温度、pH、溶氧(DO)、盐度、浊度、氨氮、生物需氧量等对养殖产品的生长环境有巨大影响的水质参数。其中涉及的氨氮质量浓度是反应水体污染程度的一个重要指标,游离态的氨氮到了一定质量浓度会对水生生物有毒害作用。
1.2 氨氮在养殖水体中的反应原理
养殖水体里的氨氮以离子态和非离子态的形式存在,考虑到其非离子含量和离子含量存在一定的换算关系,借助解离平衡关系,可以通过对一些其他变量诸如海水温度、盐度、pH来确定非离子态的百分含量fp,根据测定的总氨氮的摩尔质量,推算出氨氮的含量值,其相关关系见公式(1) ~ (3)[7]:
cNH3=1.4×10-4cNH3-Nfp
(1)
fp=100/(10pKa-cpH+1)
(2)
pKa=9.245+0.002 949S+0.032 4(298-T)
(3)
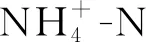
(4)
除此之外,当温度范围为0~40 ℃时,盐度与电导率、水温,存在换算公式(5)[8]:
S=1.388×d-0.024×d×t-6 171.9
(5)
式中:S表示盐度;d表示电导率,μs/cm;t表示当前水温, ℃。可见,盐度与温度和电导率有关。
另外,水中有机物进行生物氧化分解时需消耗溶氧,溶氧质量浓度关系到水中氨氮、亚硝酸盐氮和硝酸盐氮之间的转化效果[9]。
1.3 氨氮软测量建模结构
氨氮混合建模方法包括数据采集及预处理,基于机理近似的氨氮质量浓度主模型(即广义可加模型)和基于支持向量回归的氨氮质量浓度误差补偿模型等部分,结构如图1所示。因此,氨氮质量浓度的最终计算值按照公式(6)。
(6)
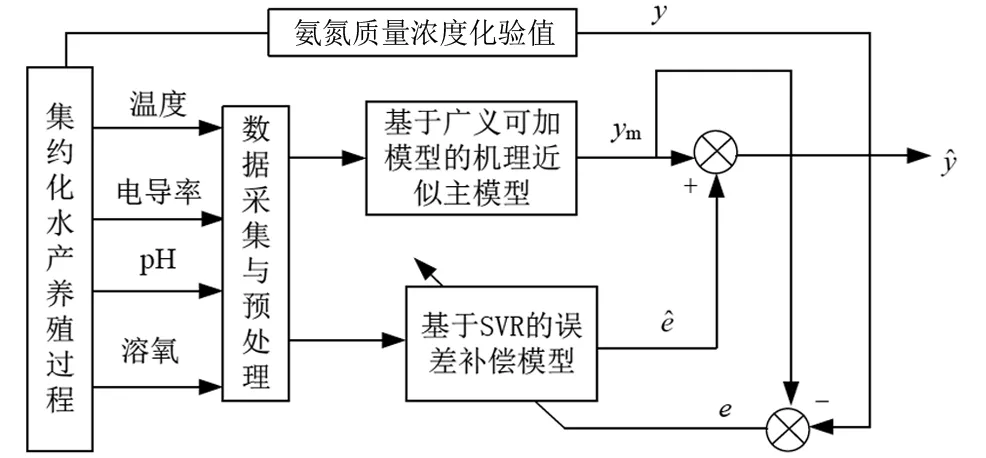

图1 氨氮软测量模型结构图
Fig.1 Soft measurement model structure of ammonia nitrogen concentration
2 基于广义可加模型的氨氮质量浓度机理近似模型
2.1 广义可加模型简介
广义可加模型属于非参数回归模型,是在广义线性模型和加性模型的基础上发展而来的,其本质是通过连接函数把因变量和每个自变量对应的光滑函数的线性和联系起来[10]。比起传统回归分析模型,其不需要满足线性假设的前提条件,能够更好地体现各变量之间复杂的非线性关系,同时还能避免维度灾难的问题。广义可加模型的基本公式[11]:
(8)
式中:μ是Y的期望值,μ=E(Y|X1,X2,…,XP);g(μ)是连接函数;sj(Xj),j=1,2,…,p是第j个自变量对应的单变量非线性光滑函数。可以采用核函数、光滑样条函数,或者局部回归光滑函数[12]。本研究采用的样条函数具有较好的整体光滑性,能及时地适应样本数据和函数的变化。
2.2 基于广义可加模型的氨氮质量浓度建模
与一般的线性模型相似,广义可加模型要求满足最小二乘法[13],可用带惩罚项的最小二乘法来估计,既能保证模型的准度,又使得样条函数在预测变量的结点处能够实现光滑,见公式(9)[14]:
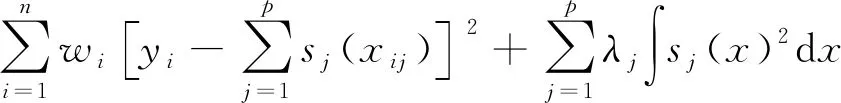
(9)
式中:wi是氨氮质量浓度模型的构造权重;sj(xij)是广义可加氨氮预测模型的单变量函数;yi表示样本的估计值;n表示样本个数;p表示变量个数。本研究包括水温、溶氧、pH和电导率4个单变量函数。λ1,λ2,…,λp是各个单变量函数的光滑参数,使用广义交叉验证GCV(λ)进行求解[15-16]:
(10)

广义可加模型的求解采用的是局部积分法[17],此算法在Fisher积分算法中整合了局部光滑方法,其中外部的Fisher积分过程用于联结函数的估计,而内部的backfitting[18]过程用于估计光滑可加项,具体计算过程参考文献[19],收敛准则为:
(11)
式中:m为迭代次数。
3 基于支持向量回归的氨氮质量浓度补偿模型
支持向量回归在小样本学习中表现出卓越的性能,具有理论完备、适应性强、模型训练时间短、泛化能力强等优势,被广泛地应用于模式识别、回归估计等领域。支持向量回归机与一般的线性回归最大的不同是,一般的线性回归只有当模型的输出与样本真值完全一致时,损失函数才为0,而支持向量回归机容忍模型与真值之间存在差值ε,当模型与真值的差值的绝对值大于ε时才计算损失。支持向量机的基本公式[20-21]:
(12)
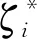
由于广义可加模型是机理近似模型,得到的模型计算值和样本的实际值存在着一定的误差,故使用支持向量回归机进行有效补偿,以同样的辅助变量为输入,广义可加模型的输出值和样本真实值的偏差作为模型的输出,建立氨氮质量浓度误差补偿模型。
4 仿真试验
4.1 数据采集与预处理
选取大菱鲆(Scophthalmusmaximus)为养殖对象,利用实验室集约化海水养殖循环水系统进行数据采集。由于仪器仪表的测量精度、测量方法、人工操作不可避免的误差等原因会使得所采集的数据不准确,可能存在异常值,所以需要数据预处理来剔除异常数据,还需避免数据的不同量纲对试验结果产生影响。采用3σ准则和数据归一化方法对数据进行预处理,部分数据如图2所示。
4.2 试验过程
4.2.1 试验内容
使用R语言,将广义可加模型写为:
(13)
式中:k为模型超参数,根据网格搜索法寻优确定其值为6,其中gam为R语言中的广义可加模型函数包。s(x0)、s(x1)、s(x2)、s(x3) 分别是水温、溶氧、电导率、pH与氨氮含量的单变量函数,a为截距。单变量对氨氮的拟合结果如图3所示。
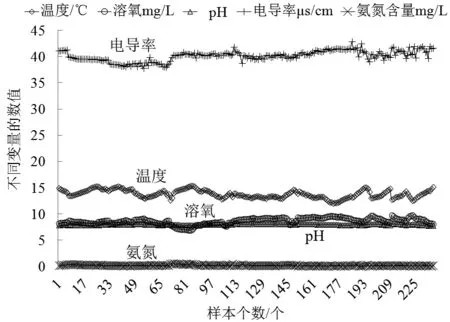
图2 部分试验数据图
单变量拟合函数图中,纵轴表示平滑函数值,函数值两边的虚线表示可信区间的上下限[22-23]。同时,伪判定系数R-sq显示了模型的解释能力为0.63,Deviance explained表明模型可解释的偏差为68%,广义交叉验证GCV的值为0.028 684,说明模型有较好的拟合效果。广义可加模型参数中,截距a的估计值为0.232,模型的标准误差为0.003,检验统计量T值为77.76,观察到的显著性水平Pr的值为2e-16。
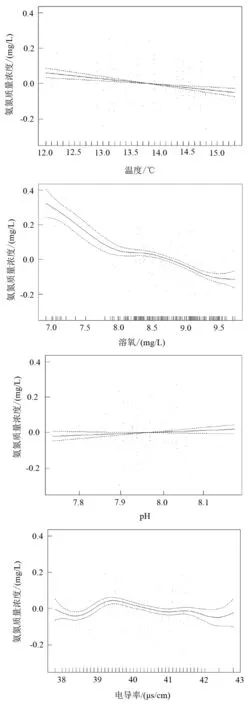
图3 单变量拟合函数图
4.2.2 试验结果
根据氨氮的反应机理,利用网格搜索法对k进行寻优,最终确定k为6,利用R语言的广义可加模型的程序包gam()函数建立广义可加模型对氨氮进行预测,得到广义可加模型的预测结果如图4所示。
由图4所示,广义可加模型的输出值,基本上可以跟踪真实值的趋势,但是存在着不小的机理误差。针对机理模型误差,采用SVR进行补偿,结果如图5(a)所示。通过将补偿前后的两个预测效果图进行分析比较,可以看出补偿前的均方根误差(RMSE)为0.079,通过SVR进行补偿后模型的均方误差降到了0.066,模型的拟合效果有较大幅度的提升。

图4 广义可加模型的拟合效果
为验证比较不同补偿模型的效果,分别采用BP神经网络和随机配置神经网络SCN[26]对机理模型进行补偿。对BP神经网络,考虑其模型精度,采用双层神经网络,每层神经元个数为25,对随机配置的神经网络SCN令隐藏层最大的层数是250,随机配置的最大次数是100,随机权重范围在0.5~250,得到的预测结果如图5(b)、(c)所示。
通过对比补偿的结果图,可以看出,在相同条件下广义可加模型加上BP网络的补偿后模型的均方根误差为0.069,与SCN网络补偿的0.068均方根误差差距不大,但是使用SVR作为补偿模型的均方根误差为0.066,具有较好的优越性。与此同时,在相同的数据集条件下,将其与单独使用BP神经网络、SCN网络[27]以及支持向量回归SVR模型[28]建立的氨氮质量浓度模型进行对比,模型的预测结果如图6(a)、(b)、(c)所示。不同方法的预测结果比较见表1。
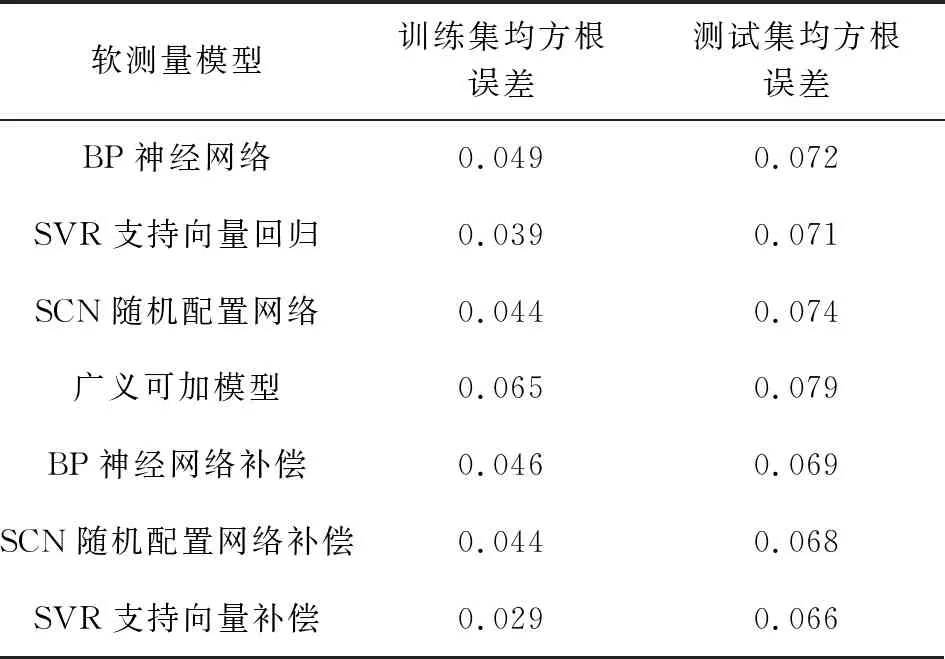
表1 不同模型的训练和测试效果比较
5 结果与讨论
5.1 支持向量机与神经网络软测量性能的对比
从表1结果可以看出,单独使用支持向量回归SVR比单独使用BP神经网络、随机配置网络SCN有较低的均方根误差,拟合效果最好;其次是随机配置网络SCN。分析原因,由于支持向量回归是建立在结构风险最小化原理上的,适用于小样本情况下研究统计学习规律。针对水环境系统的复杂性、非线性和有限样本等特性,支持向量回归正好适用于这样条件下的水质预测问题[29]。而传统BP神经网络,其模型参数在训练过程中容易陷入局部极小值[30],SCN神经网络虽然运算速度较快,但在模型的建立时需要大量的样本,故对于小样本数据,利用这两种方法建立的模型在预测精度上不及SVR的效果,与通过仿真得出来的结论一致。

图5 不同补偿模型的预测结果
5.2 混合模型带来的改进
通过混合建模的方式将广义可加模型与支持向量回归相结合,通过训练集和测试集的对比,可见混合模型比单独使用支持向量回归SVR、BP神经网络、随机配置网络SCN的软测量结果要好。虽然广义可加机理近似模型在单独模型预测上有较高的均方误差,预测效果较其他数据驱动模型差,但由于其利用了机理信息,其预测结果基本能较好反映数据变化趋势(图4)。将数据驱动模型和利用机理信息的广义可加模型相结合,能够充分利用二者的优势。通过结果比较可以看出,加入补偿模型之后,支持向量回归补偿模型的均方根误差无论是在训练集还是在测试集的表现上都优于其他的数据驱动模型,模型精度更高,泛化能力更好,并且模型的变化趋势能够更贴近数据的分布特点,使得模型的预测能力较原来的软测量模型有很大的提升。
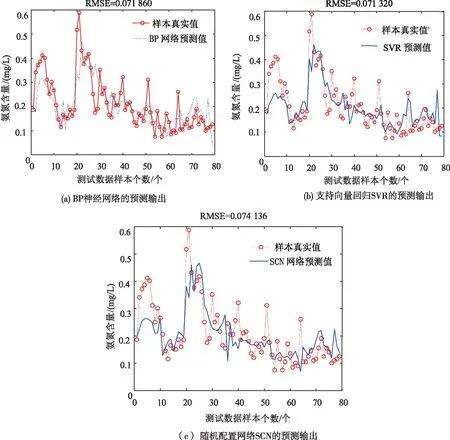
图6 不同方法单独建模的预测结果
6 结论
根据养殖水体中氨氮的机理分析,采用广义可加模型进行氨氮含量软测量,并结合网格搜索法求解广义可加模型的超参数,利用SVR算法进行了补偿。通过对比使用单一的BP神经网络,SCN神经网络的预测结果,可以看出基于氨氮在养殖水体的反应机理建立的广义可加模型,在统计学的角度上有较高的解释性。除此之外,广义可加模型是一种非参数模型,建立起来较为简单,适用于小样本数据,故选择SVR配合广义可加模型进行混合建模。试验结果表明,混合模型具有较低的均方根误差,更适合养殖过程氨氮的实时检测。
□

