基于BP神经网络算法的河湖生态健康评价研究

张天琪

(江苏省泰州引江河管理处， 江苏 泰州 225300)

1 概 述

近年来，随着经济发展带来河、湖等水环境污染、水资源短缺问题。健康的河湖生态环境对促进当地生态平衡、生物多样性等发挥着至关重要的作用。因此，建立一套既符合理论，又满足实际需求的河湖生态健康评价方法迫在眉睫。

针对河湖生态健康评价方法，众多专家和学者展开大量而深入的研究。崔东文等[1]通过筛选河流生态健康评价指标，利用随机森林算法建立河湖生态评价模型。王桂林等[2]利用权重系数法对相同准则层下的不同指标层系数赋予不同权重数值，通过求和方式计算判定河流的生态健康程度。张智伟[3]通过考虑河流的自然和社会共计38个量化属性，构建目标层、准则层等5层体系，以此来量化河流的健康程度。段长桂等[4]通过克服投影寻踪模型求解方法的缺点，借助于猴群算法对河流健康进行评价。上述针对河湖生态健康评价方法存在对指标赋权人为主观性大、建模复杂困难、精度低等不足之处。

考虑上述应用背景的特殊性，基于BP(back propagation)神经网络算法的河湖生态健康评价方法被提出。本文通过构建BP神经网络架构，选取合适的输入层、隐藏层以及输出层节点个数，学习归纳输入层到输出层的映射关系，从而可以有效对河湖的生态健康状况进行评价。

2 BP神经网络算法简介及训练步骤

2.1 BP神经网络算法简介

BP神经网络属于人工智能算法，由于其不涉及状态变量的建模问题，主要利用数据驱动的思想同时借助于大量的训练数据来实现对权重和阈值的寻优操作。BP神经网络的计算主要包括前向和反向传播。BP神经网络架构如图1所示，其主要包括输入层，隐含层和输出层。

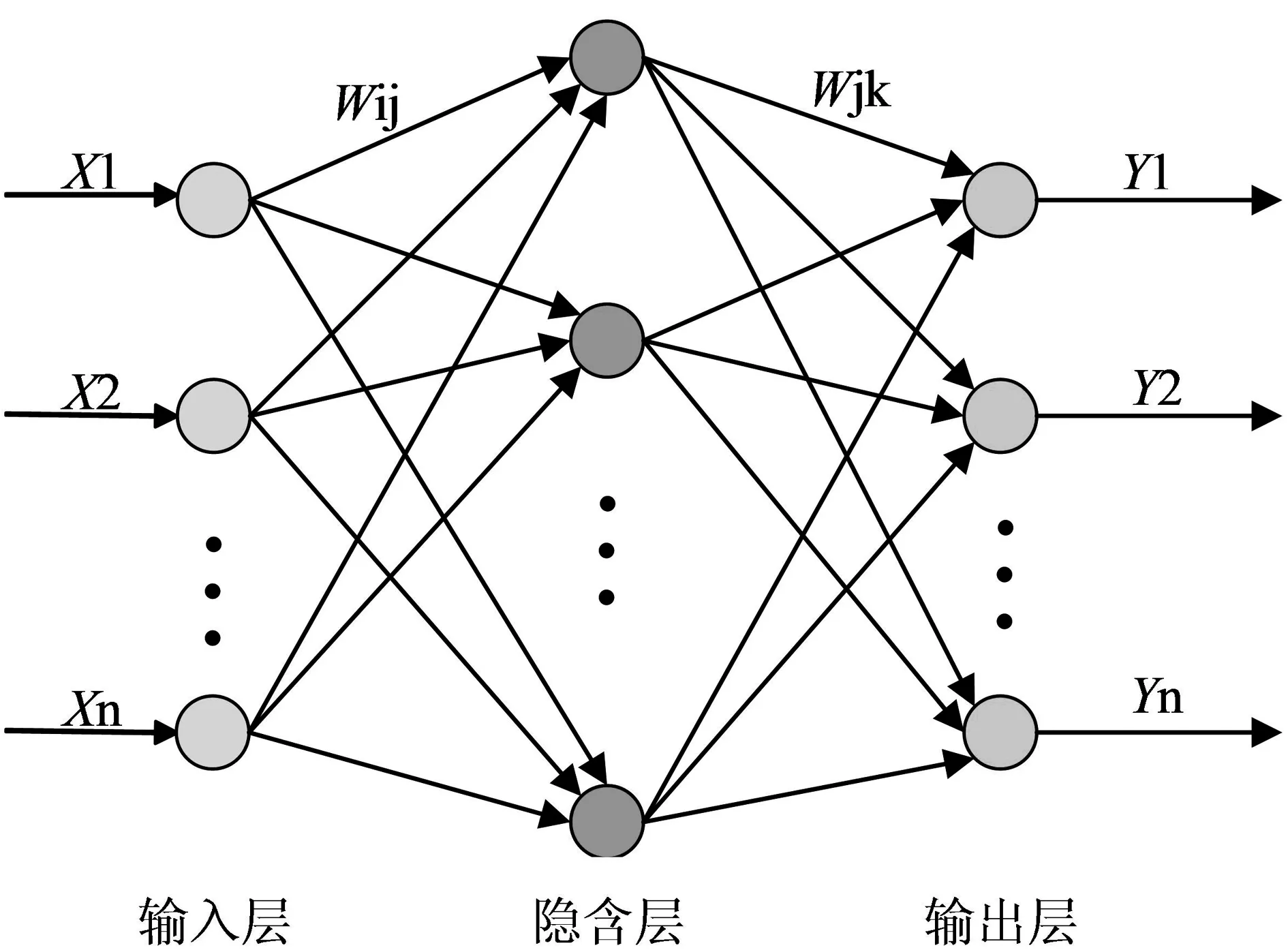
图1 BP神经网络架构

2.2 BP神经网络训练步骤

BP神经网络的训练步骤如下所示，主要涉及到BP神经网络模型的初始化操作，模型的构建以及权重更新等。

对河湖健康评价模型中的权重进行随机初始化，利用反正切函数归一化：

(1)

将BP神经网络的状态参量进行整合，并且作为输入层的输入向量，输入层节点的个数主要取决于河湖健康评价系统中不相关评价指标的个数：

X=(x1,x2,...,xi,...,xn)T

(2)

计算河湖健康评价系统中单个隐含节点的输出。根据向量X、权值wij和阈值a，求隐含层输出H，其主要是借助不同的权重系数将河湖健康评价系统中的评价指标耦合在一起。单个隐含层节点输出为

netj=w1jx1+w2jx2+...+wnjxn

(3)

最终隐含层单个神经元的输出：

Hj=f(netj-aj)

(4)

计算隐藏层所有节点的输出。由于所建立的隐藏层的层数和隐藏层节点的个数不止一个。因此，假定隐藏层的节点数目为l，将所有的输出归一化操作，则隐含层的输出向量：

H=(H1,H2,...,Hj,...,Hl)T

(5)

计算输出层节点输出大小。BP网络所具备强大的回归能力和拟合能力，原因在于隐藏层是多层结构以及每一层具备多个节点。将所有隐藏层节点的输出综合起来作为下一隐藏层节点的输入，以此类推可以使得BP神经网络自动的向前传播。最后根据输出层H、权值wjk和阈值b，可以求得BP神经网络的预测输出值O。输出层各神经元的输出值：

netk=w1kH1+w2kH2+...+wlkHl

(6)

最终输出层单个神经元的输出值：

Ok=g(netk-bk)

(7)

输出层期望得到的健康指数表示为

Y=(y1,y2,...,yk,...,ym)T

(8)

计算河湖生态健康系统预测误差。河湖健康评价系统得到的预测健康指数与期望得到的健康指数存在误差，误差值大小代表河湖健康评价系统准确度大小。通过期望输出Y和预测输出O求预测误差e：

ek=Yk-Ok

(9)

由于河湖健康评价系统的期望值与预测值存在误差，BP神经网络通过反向传播调整权重将误差缩小。根据预测误差e求解新的权值wij，wjk：

(10)

通过不断循环迭代上述计算过程，会使得河湖健康评价系统的预测健康指数和期望健康指数之间的差距越来越小。

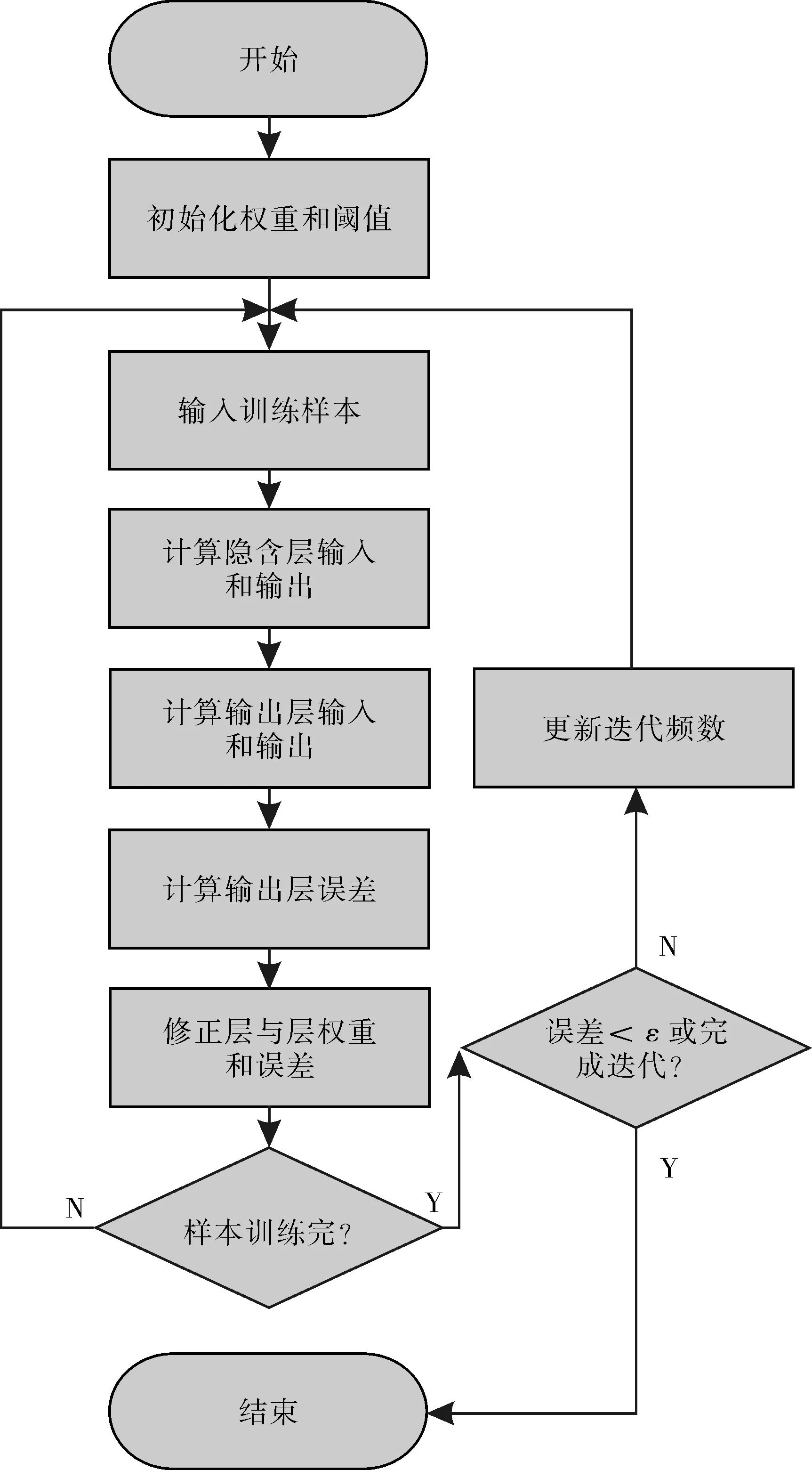
图2 BP神经网络算法示意

为了能够更加清晰地表述BP算法的更新权值和阈值的过程，可用图 2表示。当网络误差达到预设精度，则结束BP神经网络算法的迭代过程。否则，重复以上过程，直到满足停止条件。

3 河湖生态健康评价体系

3.1 评价指标筛选与确定

利用BP神经网络对河湖生态健康评价系统进行研究的过程中，需要全面考虑影响河湖生态健康的各层面指标。力求做到各指标之间不冗余、可区分性大、覆盖面广、可充分代表河湖生态健康的主要特征。

3.2 河湖生态健康评价分级

本研究将18项评价指标按照标准进行划分，除此之外，将河湖的生态健康评价共分为5类：健康、微健康、亚健康、微病态以及病态[5]，为便于利用数字化的方式对BP神经网络进行训练和测试，将上述的河湖生态健康分别用0，1，2，3，4进行表示[6]。

3.3 河湖生态健康评价指标的样本处理

收集江苏省近几年河海生态的相关资料，构造训练和测试样本。在标准的阈值范围内采用随机生成的方法构造200组样本，其中前170组用于BP神经网络模型的训练，最后30组用于检验模型。所生成样本类型，见表1。

本研究将影响河湖生态健康的指标分为4类，其分别是：水文特征、水质特征、水生态特征以及社会服务特征。每一个大类中包括若干河湖生态健康评价指标[5]，共计18项评价指标。

4 BP神经网络训练结果

本研究根据河湖评价指标设定输出层的个数为18个，根据实际的需求将隐含层的数量设置为3层[7-8]，隐藏层的数目分别是50、30、50。依据河湖健康评价等级将输出层的节点个数设置为5个。同时设定BP神经网络超参数：系统迭代误差为0.001，BP神经网络的迭代次数为1 000次，最终的训练曲线见图3。

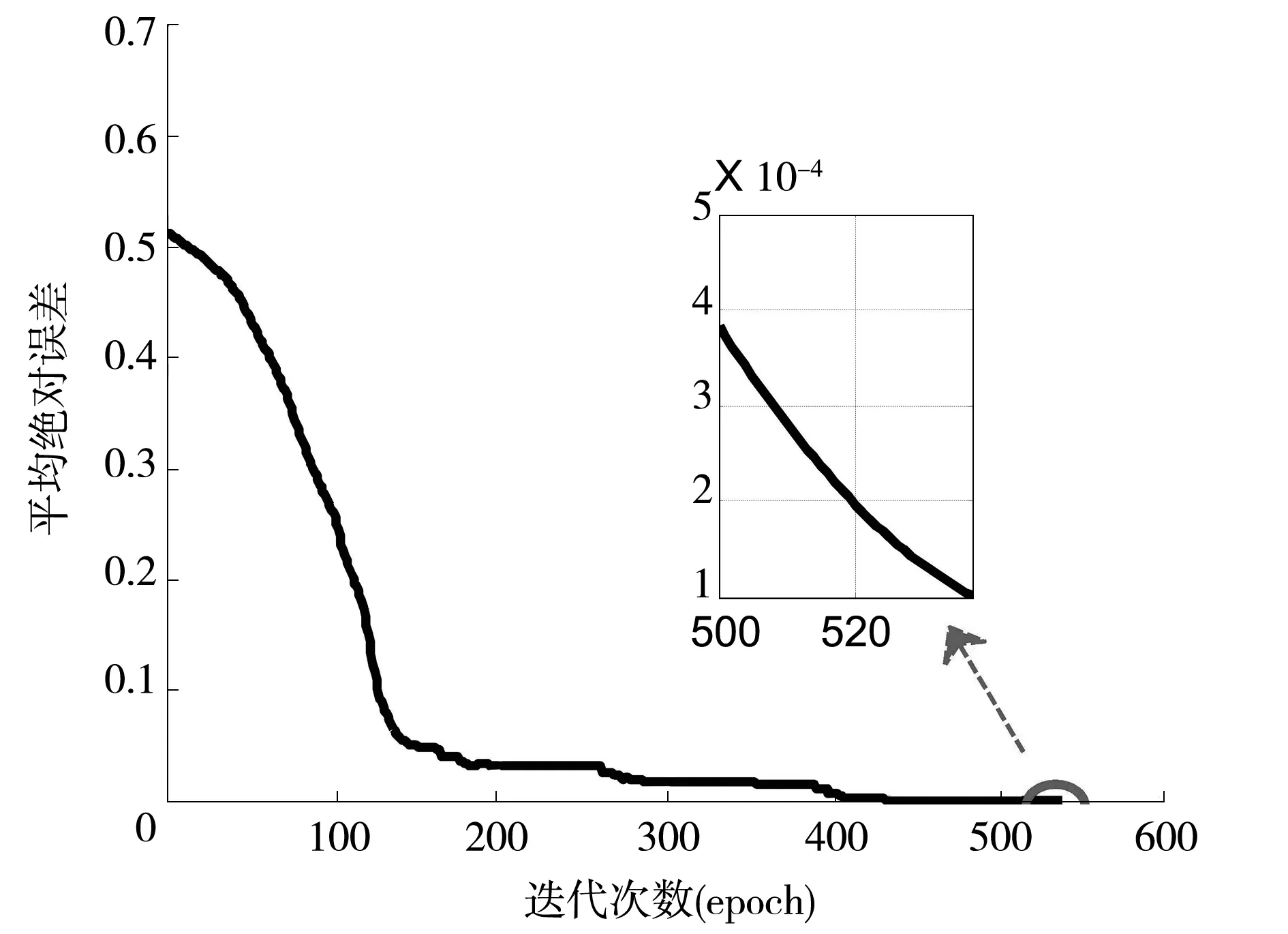
图3 误差结果

图3为BP神经网络对河湖生态健康评价系统中训练样本的结果，随着迭代的进行，BP神经网络训练误差呈现下降的趋势，特别是在训练初期，误差下降迅速。在迭代的后期，BP神经网络呈现收敛趋势，误差下降缓慢。图4是学习率的变化图，从图中可以看出，学习率逐步下降。图5是梯度变化值，从图中可以看出，在迭代的初期梯度值迅速下降，在迭代的后期梯度值几乎不变。整个BP神经网络算法在迭代次数为537次的时候，满足所设置的误差需求，停止迭代。

5 河湖生态健康评价测试

为了证明本研究针对河湖生态健康评价系统所提出的BP神经网络算法的有效性，本文将上述所得到的BP神经网络模型应用到河湖生态健康评价测试集，结果如图6所示。

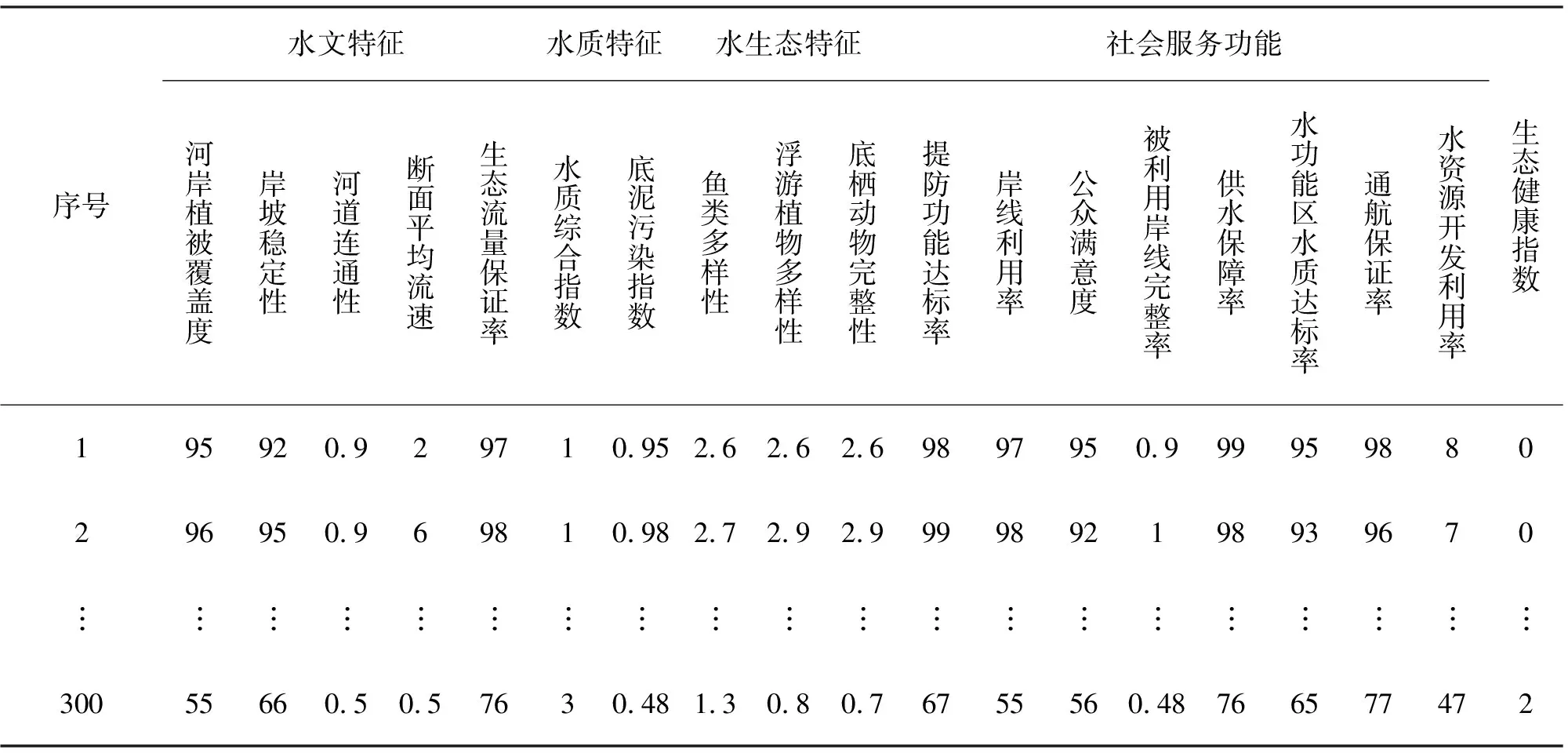
表1 河湖生态健康评价指标

图4 学习率曲线

图5 梯度变化曲线

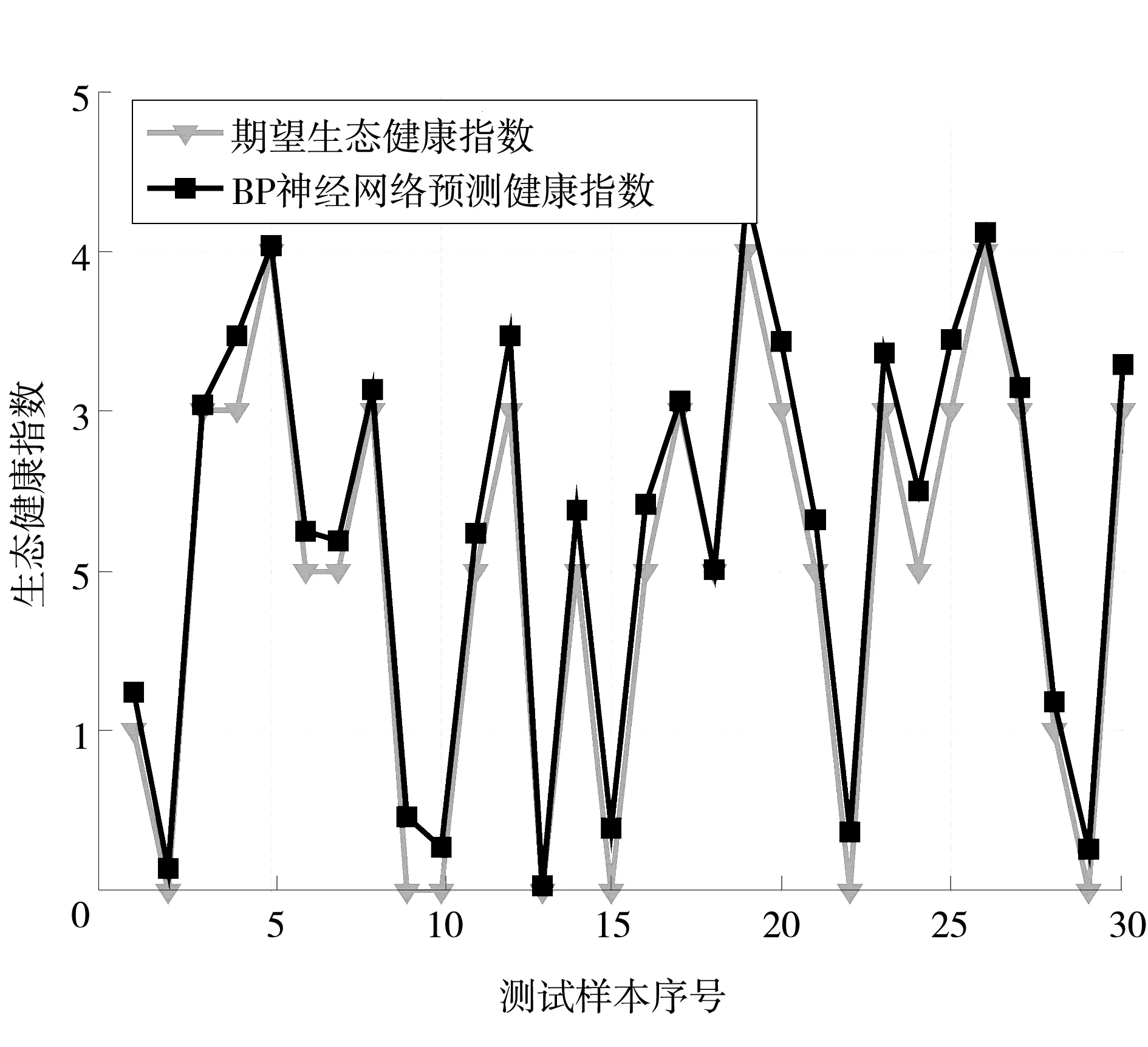
图6 BP神经网络测试结果

图6表示的是BP神经网络对河湖生态健康预测结果。测试样本的个数为30个。纵坐标代表生态健康指数，横坐标代表所测试样本的序号。其中图中红色曲线代表河湖生态期望生态健康指数，蓝色曲线代表使用BP神经网络算法对河湖生态健康预测结果。可以看出，BP神经网络预测的蓝色曲线基本与期望的红色曲线相吻合，证明了本研究所提出算法的有效性。

6 结 语

本文通过搭建BP神经网络模型、确立河湖生态健康评价指标，利用BP神经网络算法对河湖生态健康样本进行学习归纳，最终可针对河湖生态健康指数做出预测。同时可将所获得的BP神经网络预测模型应用到工程实践当中，为河湖生态健康预测提供一定的研究基础。